2021-2022学年人教版数学七年级下册第七章7.1平面直角坐标系 同步习题(word版含解析)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册第七章7.1平面直角坐标系 同步习题(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 99.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-30 19:33:57 | ||
图片预览



文档简介
人教版数学七年级下册第七章7.1平面直角坐标系
一、选择题(本大题共10小题,共30.0分)
课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用表示,小军的位置用表示,那么你的位置可以表示成
A.
B.
C.
D.
莫小贝从学校出发先向正南方向走,再向正东方向走就可到家,如果以学校为原点,以正北、正东为正方向,则她家用有序数对可表示为:
A. B. C. D.
根据下列描述能确定平面内点位置的是
A. 学校报告厅排 B. 中山二路
C. 南偏东 D. 东经,北纬
已知点在轴上,点在轴上,则点在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
以下说法:在第三象限;到轴的距离是;在轴上,则的值是;在轴的负半轴上.正确的个数是
A. B. C. D.
下列说法错误的是
A. 平面内两条互相垂直的数轴就构成了平面直角坐标系
B. 平面直角坐标系中两条坐标轴是互相垂直的
C. 坐标平面被两条坐标轴分成了四个部分,每个部分称为象限
D. 坐标轴上的点不属于任何象限
笛卡儿是法国著名的数学家,他首先提出并创建了坐标的思想,引入坐标和变量的概念,平面直角坐标系很好地体现了一种数学思想,这种数学思想是
A. 数形结合 B. 类比 C. 分类讨论 D. 建模
已知点在第二象限,到轴的距离是,到轴的距离是,点的坐标为
A. B. C. D.
在平面直角坐标系中,点位于哪个象限?
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
若点到两坐标轴的距离相等,则点的坐标
A. B.
C. 或 D. 或
二、填空题
若影院排号的座位记作,则表示的座位是_______.
已知点在第一象限角平分线上,则的值为______.
第二象限内的点满足,,则点的坐标是_________.
若点在轴上,则的值为______.
三、解答题
如图,点表示放置个胡萝卜、棵青菜,点表示放置个胡萝卜、棵青菜.
请你写出其他各点,,,所表示的意义;
若一只兔子从到达顺着方格线走,有以下几条路可以选择:
;
;
.
请帮兔子选一条路,使它吃到的食物最多.
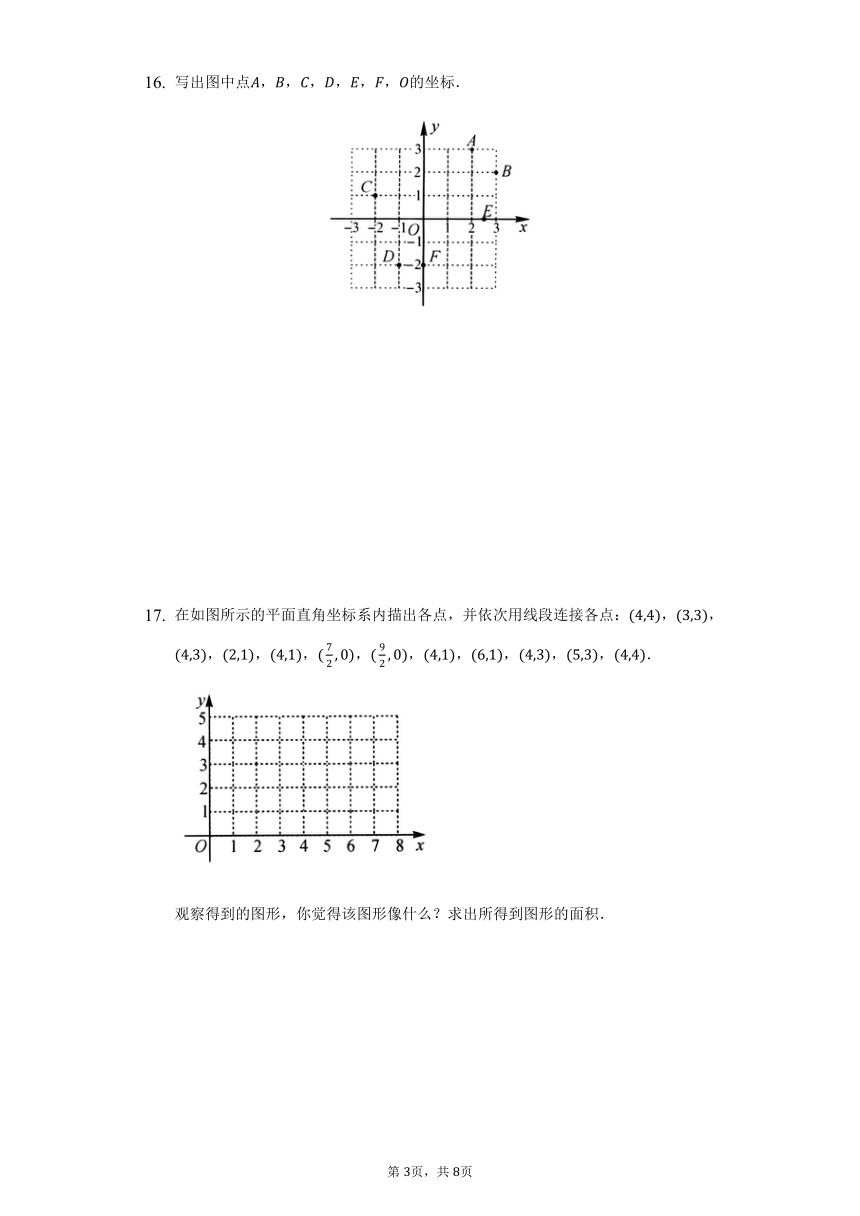
写出图中点,,,,,,的坐标.
在如图所示的平面直角坐标系内描出各点,并依次用线段连接各点:,,,,,,,,,,,.
观察得到的图形,你觉得该图形像什么?求出所得到图形的面积.
已知平面直角坐标系中有一点.
若点到轴的距离为,求的值;
若点到轴的距离为,求的值.
答案和解析
1.【答案】
【解析】解:如图所示:
你的位置可以表示成,
故选:.
因为小华的位置用表示,即为原点,由此得小刚的坐标.
2.【答案】
【解析】解:以学校位置为原点,以正北、正东为正方向,建立直角坐标系因为小敏的家在学校正南,正东方向处,
所以用有序实数对表示为.
故选C.
3.【答案】
【解析】解:学校报告厅排、中山二路、南偏东不能确定位置,
东经,北纬能确定位置.
故选D.
4.【答案】
【解析】解:点在轴上,
,
解得,
点在轴上,
,
,
点的坐标为,
在第二象限.
故选B.
5.【答案】
【解析】
解:在第二象限,故原说法错误;
到轴的距离是,说法正确;
在轴上,则,解得,故原说法错误;
在轴的负半轴上,故原说法错误.
所以正确的说法有个.
故选B.
6.【答案】
【解析】略
7.【答案】
【解析】平面直角坐标系中的点与坐标一一对应,
是数坐标与形点的结合,反映了数形结合的数学思想.
故选A.
8.【答案】
【解析】解:位于第二象限,到轴的距离为,到轴的距离为,则点的坐标为,
故选:.
根据第二象限内点到轴的距离是点的纵坐标,点到轴的距离是横坐标的相反数,可得答案.
本题考查了点的坐标,第二象限内点到轴的距离是点的纵坐标,点到轴的距离是横坐标的相反数.
9.【答案】
【解析】解:点坐标为,则它位于第四象限,
故选:.
10.【答案】
【解析】解:点到两坐标轴的距离相等,
,
或或或,
解得或,
点的坐标为或;
故选D.
11.【答案】排号
【解析】解:排号可以用表示,
则表示排号,
故答案为:排号.
若影院排号的座位记作,则表示的座位是排号.据此解答.
本题考查的是有序数对,理解有序数对的意义是解题的关键.
12.【答案】
【解析】解:根据题意得,
解得,
即的值为.
故答案为:.
13.【答案】
【解析】解:,,
,,
第二象限内的点,
,,
,,
点的坐标为.
故答案为.
14.【答案】
【解析】解:点在轴上,
,
解得.
故答案为:.
15.【答案】解:表示放置个胡萝卜、棵青菜;
表示放置个胡萝卜、棵青菜;
表示放置个胡萝卜、棵青菜;
表示放置个胡萝卜、棵青菜.
走有个胡萝卜、棵青菜;
走有个胡萝卜、棵青菜;
走有个胡萝卜、棵青菜.
故兔子选择路线吃到的胡萝卜、青菜都最多.
16.【答案】解:观察图,得,,,,,,
.
17.【答案】解:图略,该图形像宝塔松.
图形的面积为.
【解析】略
18.【答案】解:,点到轴的距离为,
,
解得:或;
,点到轴的距离为,
,
解得:或.
第2页,共2页
第1页,共1页
一、选择题(本大题共10小题,共30.0分)
课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用表示,小军的位置用表示,那么你的位置可以表示成
A.
B.
C.
D.
莫小贝从学校出发先向正南方向走,再向正东方向走就可到家,如果以学校为原点,以正北、正东为正方向,则她家用有序数对可表示为:
A. B. C. D.
根据下列描述能确定平面内点位置的是
A. 学校报告厅排 B. 中山二路
C. 南偏东 D. 东经,北纬
已知点在轴上,点在轴上,则点在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
以下说法:在第三象限;到轴的距离是;在轴上,则的值是;在轴的负半轴上.正确的个数是
A. B. C. D.
下列说法错误的是
A. 平面内两条互相垂直的数轴就构成了平面直角坐标系
B. 平面直角坐标系中两条坐标轴是互相垂直的
C. 坐标平面被两条坐标轴分成了四个部分,每个部分称为象限
D. 坐标轴上的点不属于任何象限
笛卡儿是法国著名的数学家,他首先提出并创建了坐标的思想,引入坐标和变量的概念,平面直角坐标系很好地体现了一种数学思想,这种数学思想是
A. 数形结合 B. 类比 C. 分类讨论 D. 建模
已知点在第二象限,到轴的距离是,到轴的距离是,点的坐标为
A. B. C. D.
在平面直角坐标系中,点位于哪个象限?
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
若点到两坐标轴的距离相等,则点的坐标
A. B.
C. 或 D. 或
二、填空题
若影院排号的座位记作,则表示的座位是_______.
已知点在第一象限角平分线上,则的值为______.
第二象限内的点满足,,则点的坐标是_________.
若点在轴上,则的值为______.
三、解答题
如图,点表示放置个胡萝卜、棵青菜,点表示放置个胡萝卜、棵青菜.
请你写出其他各点,,,所表示的意义;
若一只兔子从到达顺着方格线走,有以下几条路可以选择:
;
;
.
请帮兔子选一条路,使它吃到的食物最多.
写出图中点,,,,,,的坐标.
在如图所示的平面直角坐标系内描出各点,并依次用线段连接各点:,,,,,,,,,,,.
观察得到的图形,你觉得该图形像什么?求出所得到图形的面积.
已知平面直角坐标系中有一点.
若点到轴的距离为,求的值;
若点到轴的距离为,求的值.
答案和解析
1.【答案】
【解析】解:如图所示:
你的位置可以表示成,
故选:.
因为小华的位置用表示,即为原点,由此得小刚的坐标.
2.【答案】
【解析】解:以学校位置为原点,以正北、正东为正方向,建立直角坐标系因为小敏的家在学校正南,正东方向处,
所以用有序实数对表示为.
故选C.
3.【答案】
【解析】解:学校报告厅排、中山二路、南偏东不能确定位置,
东经,北纬能确定位置.
故选D.
4.【答案】
【解析】解:点在轴上,
,
解得,
点在轴上,
,
,
点的坐标为,
在第二象限.
故选B.
5.【答案】
【解析】
解:在第二象限,故原说法错误;
到轴的距离是,说法正确;
在轴上,则,解得,故原说法错误;
在轴的负半轴上,故原说法错误.
所以正确的说法有个.
故选B.
6.【答案】
【解析】略
7.【答案】
【解析】平面直角坐标系中的点与坐标一一对应,
是数坐标与形点的结合,反映了数形结合的数学思想.
故选A.
8.【答案】
【解析】解:位于第二象限,到轴的距离为,到轴的距离为,则点的坐标为,
故选:.
根据第二象限内点到轴的距离是点的纵坐标,点到轴的距离是横坐标的相反数,可得答案.
本题考查了点的坐标,第二象限内点到轴的距离是点的纵坐标,点到轴的距离是横坐标的相反数.
9.【答案】
【解析】解:点坐标为,则它位于第四象限,
故选:.
10.【答案】
【解析】解:点到两坐标轴的距离相等,
,
或或或,
解得或,
点的坐标为或;
故选D.
11.【答案】排号
【解析】解:排号可以用表示,
则表示排号,
故答案为:排号.
若影院排号的座位记作,则表示的座位是排号.据此解答.
本题考查的是有序数对,理解有序数对的意义是解题的关键.
12.【答案】
【解析】解:根据题意得,
解得,
即的值为.
故答案为:.
13.【答案】
【解析】解:,,
,,
第二象限内的点,
,,
,,
点的坐标为.
故答案为.
14.【答案】
【解析】解:点在轴上,
,
解得.
故答案为:.
15.【答案】解:表示放置个胡萝卜、棵青菜;
表示放置个胡萝卜、棵青菜;
表示放置个胡萝卜、棵青菜;
表示放置个胡萝卜、棵青菜.
走有个胡萝卜、棵青菜;
走有个胡萝卜、棵青菜;
走有个胡萝卜、棵青菜.
故兔子选择路线吃到的胡萝卜、青菜都最多.
16.【答案】解:观察图,得,,,,,,
.
17.【答案】解:图略,该图形像宝塔松.
图形的面积为.
【解析】略
18.【答案】解:,点到轴的距离为,
,
解得:或;
,点到轴的距离为,
,
解得:或.
第2页,共2页
第1页,共1页
