【2012优化方案 精品课件】苏教版 数学 选修1-1 第1章常用逻辑用语 常用逻辑用语总结
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 选修1-1 第1章常用逻辑用语 常用逻辑用语总结 |

|
|
| 格式 | zip | ||
| 文件大小 | 597.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-22 08:09:21 | ||
图片预览










文档简介
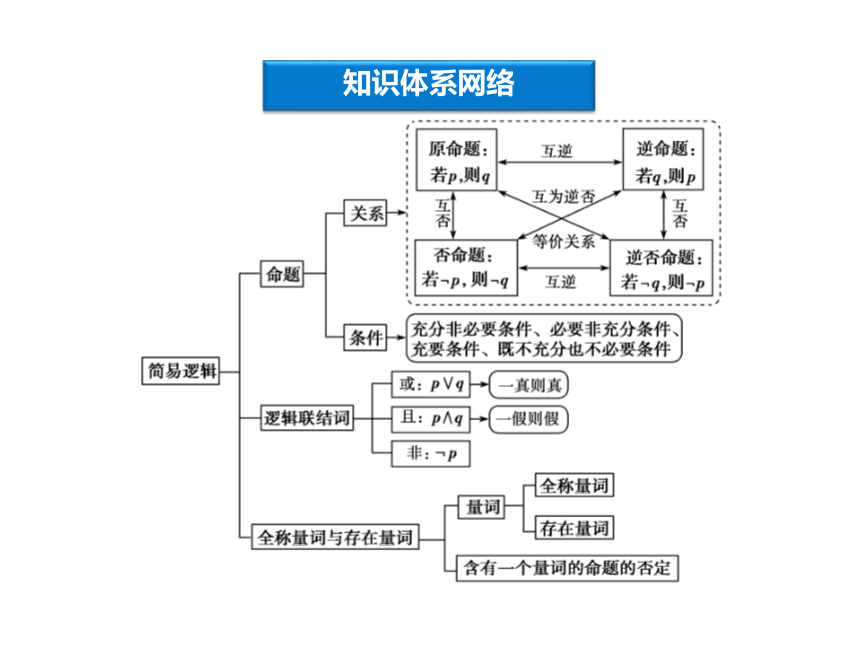
课件33张PPT。本章优化总结 专题探究精讲章末综合检测本章优化总结知识体系网络知识体系网络专题探究精讲命题真假的判断是高考考查的重要内容之一,是高考的热点题型.这类题型一般涉及到一些一般命题真假的判断、含有逻辑联结词的命题真假的判断、含有一个量词的命题真假的判断、命题的四种形式中真假的判断等.并且这类题型一般不会单独命题,往往与其他相关的数学知识结合起来进行考查,且主要以填空题的形式出现.1.判断一般命题的真假【答案】 ①②③④【名师点评】 命题真假的判断等问题往往会将所学习过的知识综合起来,既考查对命题等概念的理解,又考查相应的数学知识,是高考的热点题型.解决这类问题时,一定要熟悉相关的数学知识.2.根据四种命题间的关系判断真假
命题“若C=90°,则△ABC是直角三角形”与它的逆命题、否命题、逆否命题这4个命题中,真命题的个数是________.【解析】 对于原命题来说,是真命题.其逆命题为“若△ABC是直角三角形,则C=90°”,这是一个假命题,因为当△ABC为直角三角形时,A、B也可能为直角.这样,否命题是假命题,逆否命题是真命题.因此真命题的个数是2.
【答案】 2【名师点评】 判断命题的真假,除了直接对命题本身进行判断外,还可以根据命题的等价性进行判断.事实上,在命题的四种形式中,真命题的个数一定为偶数,因为原命题与逆否命题同真同假,逆命题与否命题同真同假.3.判断含有逻辑联结词的命题的真假
已知命题p:不等式x(x-1)<0的解集是{x|0①p真q假 ②p∧q为真 ③p∨q为假 ④p假q真【解析】 对于命题p,由x(x-1)<0,解得0对于命题q,由A=B,一定有sin A=sin B,但当sin A=sin B时,不一定有A=B,所以“A=B”是“sin A=sin B”成立的充分而不必要条件,因此命题q为假命题.
【答案】 ①【名师点评】 对含有逻辑联结词的命题而言,其真假的判断主要根据逻辑联结词的含义和真值表进行,但首先应搞清楚每一个简单命题的真假.处理充要条件的问题,首先要弄清充分条件、必要条件、充要条件的概念,其次要会利用“定义法”“集合法”“四种命题关系法”“逆推法”等来判定充要条件的问题.1.判断是何种条件
设函数f(x)=ax+b(0≤x≤1),p:a+2b>0,q:f(x)>0恒成立,则p是q的________条件.【答案】 必要不充分
【名师点评】 在进行充分、必要条件的判断时,要注意问题的设问方式.例如A是B的充分而不必要条件是指:A?B且B A;而A是B的必要不充分条件是指:B?A且A B.这是在充要条件的推理判断中经常出现且容易混淆的两种说法,在解题中一定要注意问题的设问方式,弄清它们的区别,以免出现错误判断.2.求充要条件
对于实数x,规定[x]表示不大于x的最大整数,那么不等式4[x]2-36[x]+45<0成立的充分必要条件是________.【答案】 [2,8)
【名师点评】 解题的关键在于利用换元法将不等式转化为一元二次不等式,然后根据所给出的定义进行求解,要搞清楚充分必要条件的含义.3.根据条件求参数的取值范围
已知p:x2-8x-20>0,q:x2-2x+1-a2>0,若p是q的充分而不必要条件,求正实数a的取值范围.
【思路点拨】 p是q的充分不必要条件,即p?q且q p,利用集合间的包含关系求a的范围.【解】 解不等式x2-8x-20>0,得p:A={x|x>10或x<-2};
解不等式x2-2x+1-a2>0,得q:B={x|x>1+a或x<1-a,a>0}.
依题意p?q但q p,说明A B.【名师点评】 可以利用集合之间的包含关系对充要条件进行判断,如果命题p和q所涉及的问题对应的集合分别为A、B,则具体情况如下:(1)若A?B,则p是q的充分条件;(2)若A?B,则p是q的必要条件;(3)若A=B,则p是q的充要条件.根据充分、必要条件求参数取值范围时,可先找到相应集合之间的包含关系,再求解参数的取值范围.根据简单命题的真假,利用真值表判断复合命题的真假,要掌握以下规律:
(1)“p或q”形式的复合命题:只有当命题“p”与命题“q”同为假时才为假,否则都为真;
(2)“p且q”形式的复合命题:只有当命题“p”与命题“q”同为真时才为真,否则都为假;
(3)“非p”形式的复合命题:其真假与命题“p”的真假相反. 已知命题p:关于x的不等式x2+2ax+4>0对?x∈R恒成立;命题q:函数y=-(4-2a)x是R上的减函数.若“p∨q”为真命题,“p∧q”为假命题,则实数a的取值范围是________.【名师点评】 先简化两个命题,并求出两个命题为真时a的范围,最后根据题中命题的关系确定出a的取值范围.在学习中,我们可以通过具体的例子来理解相关的概念,巩固知识.由于全称命题的否定是存在性命题,存在性命题的否定是全称命题,因此,我们可以通过举反例来否定一个全称命题. 已知命题p:?x∈R,(x-1)(x+2)=0,则命题p的否定是________.
【解析】 命题p是一个全称命题,其否定为存在性命题,即?x0∈R,(x0-1)(x0+2)≠0.
【答案】 ?x0∈R,(x0-1)(x0+2)≠0【名师点评】 对含有一个量词的命题进行否定,是高考考查的热点内容.解决这类问题的关键有两个,一是弄清楚原命题是全称命题还是存在性命题,从而决定其否定是全称命题还是存在性命题,选用恰当的量词符号;二是搞清楚原命题的结论是什么,在否定命题中,将其否定.章末综合检测本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
命题“若C=90°,则△ABC是直角三角形”与它的逆命题、否命题、逆否命题这4个命题中,真命题的个数是________.【解析】 对于原命题来说,是真命题.其逆命题为“若△ABC是直角三角形,则C=90°”,这是一个假命题,因为当△ABC为直角三角形时,A、B也可能为直角.这样,否命题是假命题,逆否命题是真命题.因此真命题的个数是2.
【答案】 2【名师点评】 判断命题的真假,除了直接对命题本身进行判断外,还可以根据命题的等价性进行判断.事实上,在命题的四种形式中,真命题的个数一定为偶数,因为原命题与逆否命题同真同假,逆命题与否命题同真同假.3.判断含有逻辑联结词的命题的真假
已知命题p:不等式x(x-1)<0的解集是{x|0
【答案】 ①【名师点评】 对含有逻辑联结词的命题而言,其真假的判断主要根据逻辑联结词的含义和真值表进行,但首先应搞清楚每一个简单命题的真假.处理充要条件的问题,首先要弄清充分条件、必要条件、充要条件的概念,其次要会利用“定义法”“集合法”“四种命题关系法”“逆推法”等来判定充要条件的问题.1.判断是何种条件
设函数f(x)=ax+b(0≤x≤1),p:a+2b>0,q:f(x)>0恒成立,则p是q的________条件.【答案】 必要不充分
【名师点评】 在进行充分、必要条件的判断时,要注意问题的设问方式.例如A是B的充分而不必要条件是指:A?B且B A;而A是B的必要不充分条件是指:B?A且A B.这是在充要条件的推理判断中经常出现且容易混淆的两种说法,在解题中一定要注意问题的设问方式,弄清它们的区别,以免出现错误判断.2.求充要条件
对于实数x,规定[x]表示不大于x的最大整数,那么不等式4[x]2-36[x]+45<0成立的充分必要条件是________.【答案】 [2,8)
【名师点评】 解题的关键在于利用换元法将不等式转化为一元二次不等式,然后根据所给出的定义进行求解,要搞清楚充分必要条件的含义.3.根据条件求参数的取值范围
已知p:x2-8x-20>0,q:x2-2x+1-a2>0,若p是q的充分而不必要条件,求正实数a的取值范围.
【思路点拨】 p是q的充分不必要条件,即p?q且q p,利用集合间的包含关系求a的范围.【解】 解不等式x2-8x-20>0,得p:A={x|x>10或x<-2};
解不等式x2-2x+1-a2>0,得q:B={x|x>1+a或x<1-a,a>0}.
依题意p?q但q p,说明A B.【名师点评】 可以利用集合之间的包含关系对充要条件进行判断,如果命题p和q所涉及的问题对应的集合分别为A、B,则具体情况如下:(1)若A?B,则p是q的充分条件;(2)若A?B,则p是q的必要条件;(3)若A=B,则p是q的充要条件.根据充分、必要条件求参数取值范围时,可先找到相应集合之间的包含关系,再求解参数的取值范围.根据简单命题的真假,利用真值表判断复合命题的真假,要掌握以下规律:
(1)“p或q”形式的复合命题:只有当命题“p”与命题“q”同为假时才为假,否则都为真;
(2)“p且q”形式的复合命题:只有当命题“p”与命题“q”同为真时才为真,否则都为假;
(3)“非p”形式的复合命题:其真假与命题“p”的真假相反. 已知命题p:关于x的不等式x2+2ax+4>0对?x∈R恒成立;命题q:函数y=-(4-2a)x是R上的减函数.若“p∨q”为真命题,“p∧q”为假命题,则实数a的取值范围是________.【名师点评】 先简化两个命题,并求出两个命题为真时a的范围,最后根据题中命题的关系确定出a的取值范围.在学习中,我们可以通过具体的例子来理解相关的概念,巩固知识.由于全称命题的否定是存在性命题,存在性命题的否定是全称命题,因此,我们可以通过举反例来否定一个全称命题. 已知命题p:?x∈R,(x-1)(x+2)=0,则命题p的否定是________.
【解析】 命题p是一个全称命题,其否定为存在性命题,即?x0∈R,(x0-1)(x0+2)≠0.
【答案】 ?x0∈R,(x0-1)(x0+2)≠0【名师点评】 对含有一个量词的命题进行否定,是高考考查的热点内容.解决这类问题的关键有两个,一是弄清楚原命题是全称命题还是存在性命题,从而决定其否定是全称命题还是存在性命题,选用恰当的量词符号;二是搞清楚原命题的结论是什么,在否定命题中,将其否定.章末综合检测本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
