【2012优化方案 精品课件】苏教版 数学 选修1-1 2.3.2 双曲线的几何性质
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 选修1-1 2.3.2 双曲线的几何性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 756.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-22 08:12:06 | ||
图片预览








文档简介
课件36张PPT。2.3.2 双曲线的几何性质学习目标
1.了解双曲线的几何性质.
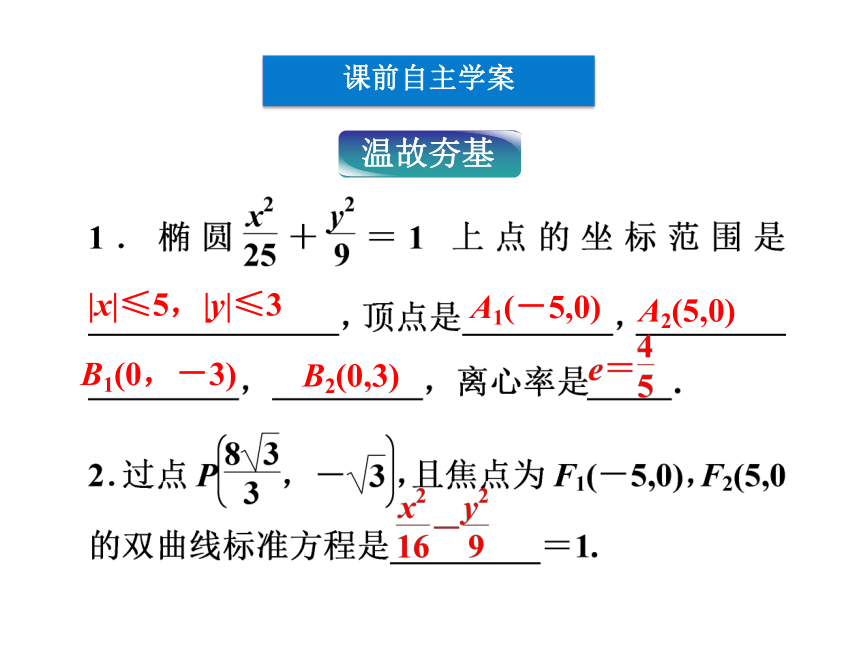
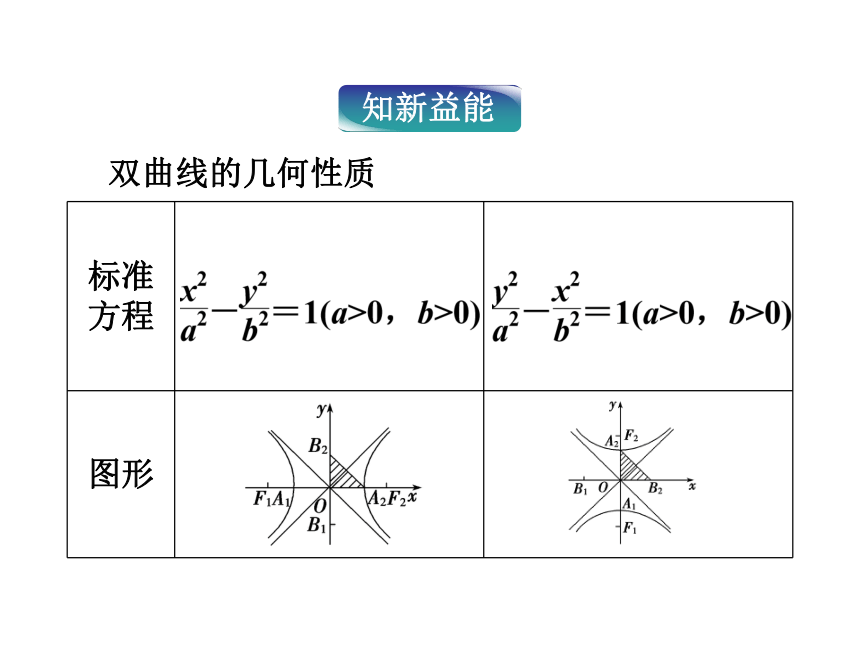
2.会用双曲线的几何性质处理简单问题. 课堂互动讲练知能优化训练2.3.2课前自主学案课前自主学案|x|≤5,|y|≤3A1(-5,0)A2(5,0)B1(0,-3)B2(0,3)双曲线的几何性质2a2b1.能不能用a,b表示双曲线的离心率?2.不同的双曲线,渐近线能相同吗?其方程有何特点?课堂互动讲练利用双曲线的几何性质,能够完成基本量a,b,c,e之间的互求;按照题中的要求,可以正确地写出范围、实轴长、虚轴长、顶点坐标、焦点坐标、渐近线方程、离心率等;根据双曲线所满足的几何条件,可以求双曲线的标准方程. 求以2x±3y=0为渐近线,且过点(1,2)的双曲线方程.
【思路点拨】 所求双曲线方程的渐近线已知,因此可用有共同渐近线的双曲线系求解,也可按焦点在坐标轴上的位置分类讨论,利用待定系数法求解.
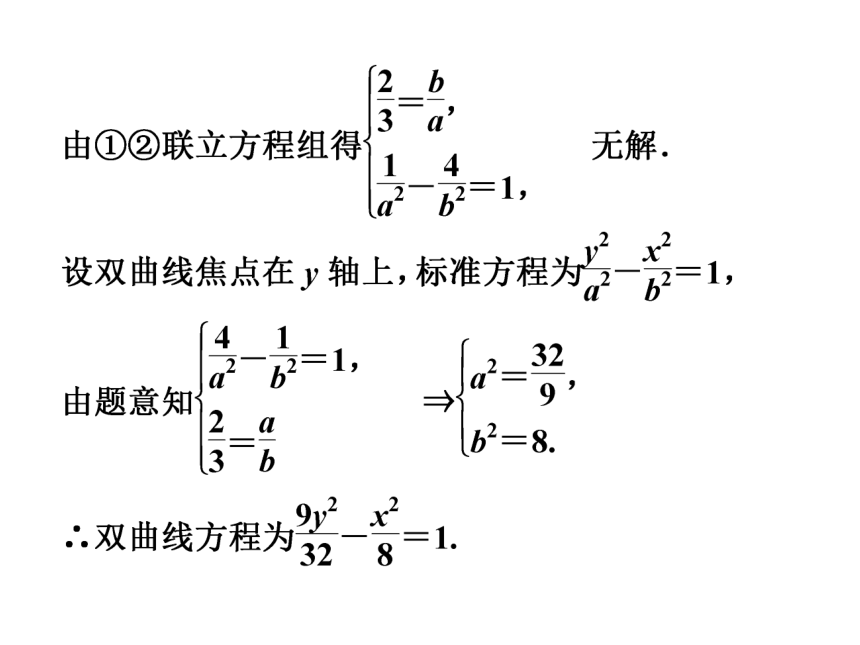
【解】 法一:设所求双曲线方程为4x2-9y2=λ(λ≠0),点(1,2)在双曲线上,将点(1,2)的坐标代入方程可得λ=-32,故所求的双曲线方程为4x2-9y2=-32,【名师点评】 (1)若已知渐近线方程为mx±ny=0,求双曲线方程.双曲线的焦点可能在x轴上,也可能在y轴上,可用下面的方法来解决.
法一:分两种情况设出方程进行讨论.
法二:依据渐近线方程,设出双曲线为m2x2-n2y2=λ(λ≠0),求出λ即可.
(2)本题法一的设法给解题带来方便,但法二是基本解法应重点掌握.【名师点评】 求双曲线的离心率就是要构造出关于a、b、c的一个方程,进而转化为关于e的方程求出结果,同时要利用好隐含条件c>a>0,确定e的取值范围.自我挑战2 (2011年高考课标全国卷改编)设直线l过双曲线C的一个焦点,且与C的一条对称轴垂直,l与C交于A,B两点,|AB|为C的实轴长的2倍,则C的离心率为________.(1)直线与双曲线的位置关系有三种:(1)直线与双曲线相交(包括有两个不同的公共点和当直线与双曲线的渐近线平行时有一个公共点两种情况);(2)直线与双曲线相切(直线与双曲线有两个重合的公共点);(3)直线与双曲线相离(没有公共点).(2)直线与双曲线的公共点就是以直线的方程与双曲线的方程联立所构成方程组的解为坐标的点,因此对直线与双曲线的位置关系的讨论,常常转化为对由它们的方程构成的方程组的讨论.(3)直线与椭圆的位置关系是由它们交点的个数决定的,而直线与双曲线的位置关系不能由其交点的个数决定. (本题满分14分)如图所示,设直线l与双曲线交于A,B两点,和双曲线的渐近线交于C,D两点,求证|AC|=|BD|.【思路点拨】 欲证|AC|=|BD|,只需证线段AB的中点与线段CD的中点重合.(2)应用双曲线的几何性质,可以解决的两类问题是:由方程研究几何性质,由几何性质求解方程.解决问题的关键都是抓住几何性质,逐步列式或直接列方程求解.
(3)解决与双曲线相关的问题,如中点弦、弦长、与直线的位置关系等,要注意运用方程思想、消元法、根与系数的关系、弦长公式等.知能优化训练本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
1.了解双曲线的几何性质.
2.会用双曲线的几何性质处理简单问题. 课堂互动讲练知能优化训练2.3.2课前自主学案课前自主学案|x|≤5,|y|≤3A1(-5,0)A2(5,0)B1(0,-3)B2(0,3)双曲线的几何性质2a2b1.能不能用a,b表示双曲线的离心率?2.不同的双曲线,渐近线能相同吗?其方程有何特点?课堂互动讲练利用双曲线的几何性质,能够完成基本量a,b,c,e之间的互求;按照题中的要求,可以正确地写出范围、实轴长、虚轴长、顶点坐标、焦点坐标、渐近线方程、离心率等;根据双曲线所满足的几何条件,可以求双曲线的标准方程. 求以2x±3y=0为渐近线,且过点(1,2)的双曲线方程.
【思路点拨】 所求双曲线方程的渐近线已知,因此可用有共同渐近线的双曲线系求解,也可按焦点在坐标轴上的位置分类讨论,利用待定系数法求解.
【解】 法一:设所求双曲线方程为4x2-9y2=λ(λ≠0),点(1,2)在双曲线上,将点(1,2)的坐标代入方程可得λ=-32,故所求的双曲线方程为4x2-9y2=-32,【名师点评】 (1)若已知渐近线方程为mx±ny=0,求双曲线方程.双曲线的焦点可能在x轴上,也可能在y轴上,可用下面的方法来解决.
法一:分两种情况设出方程进行讨论.
法二:依据渐近线方程,设出双曲线为m2x2-n2y2=λ(λ≠0),求出λ即可.
(2)本题法一的设法给解题带来方便,但法二是基本解法应重点掌握.【名师点评】 求双曲线的离心率就是要构造出关于a、b、c的一个方程,进而转化为关于e的方程求出结果,同时要利用好隐含条件c>a>0,确定e的取值范围.自我挑战2 (2011年高考课标全国卷改编)设直线l过双曲线C的一个焦点,且与C的一条对称轴垂直,l与C交于A,B两点,|AB|为C的实轴长的2倍,则C的离心率为________.(1)直线与双曲线的位置关系有三种:(1)直线与双曲线相交(包括有两个不同的公共点和当直线与双曲线的渐近线平行时有一个公共点两种情况);(2)直线与双曲线相切(直线与双曲线有两个重合的公共点);(3)直线与双曲线相离(没有公共点).(2)直线与双曲线的公共点就是以直线的方程与双曲线的方程联立所构成方程组的解为坐标的点,因此对直线与双曲线的位置关系的讨论,常常转化为对由它们的方程构成的方程组的讨论.(3)直线与椭圆的位置关系是由它们交点的个数决定的,而直线与双曲线的位置关系不能由其交点的个数决定. (本题满分14分)如图所示,设直线l与双曲线交于A,B两点,和双曲线的渐近线交于C,D两点,求证|AC|=|BD|.【思路点拨】 欲证|AC|=|BD|,只需证线段AB的中点与线段CD的中点重合.(2)应用双曲线的几何性质,可以解决的两类问题是:由方程研究几何性质,由几何性质求解方程.解决问题的关键都是抓住几何性质,逐步列式或直接列方程求解.
(3)解决与双曲线相关的问题,如中点弦、弦长、与直线的位置关系等,要注意运用方程思想、消元法、根与系数的关系、弦长公式等.知能优化训练本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
