【2012优化方案 精品课件】苏教版 数学 选修1-1 2.4.2 抛物线的几何性质
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 选修1-1 2.4.2 抛物线的几何性质 |  | |
| 格式 | zip | ||
| 文件大小 | 824.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-22 08:13:18 | ||
图片预览







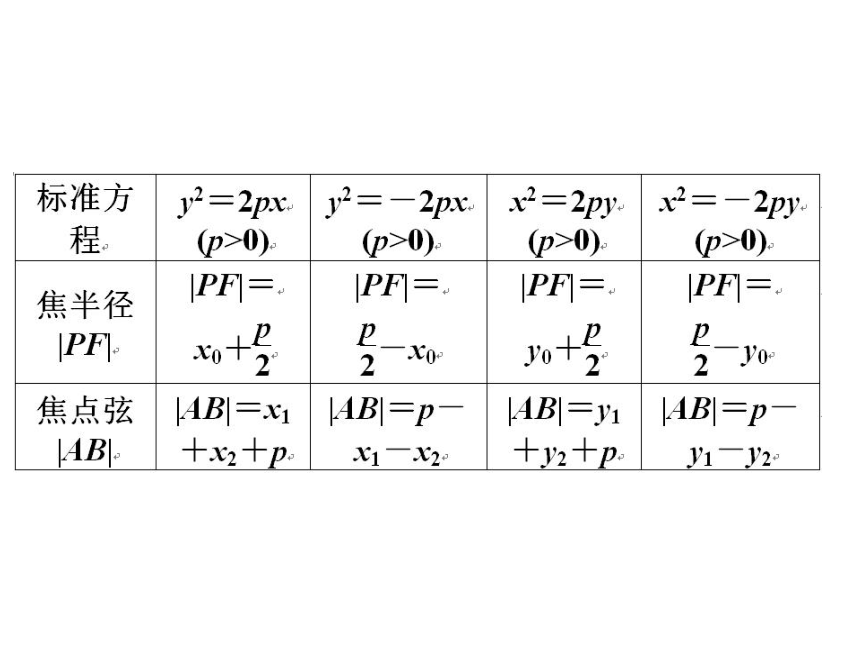


文档简介
课件46张PPT。2.4.2 抛物线的几何性质学习目标
1.掌握抛物线的几何性质.
2.会用抛物线的几何性质处理简单问题. 课堂互动讲练知能优化训练2.4.2课前自主学案课前自主学案y2=2px(p>0)x2=2py(p>0)2.抛物线定义的实质是:__________,其中,点F是抛物线的____,dM-l是抛物线上的_______________.
3.过点M(-2,4)的抛物线的标准方程是________________.|MF|=dM-l焦点点到准线的距离x2=y或y2=-8x1.抛物线的几何性质
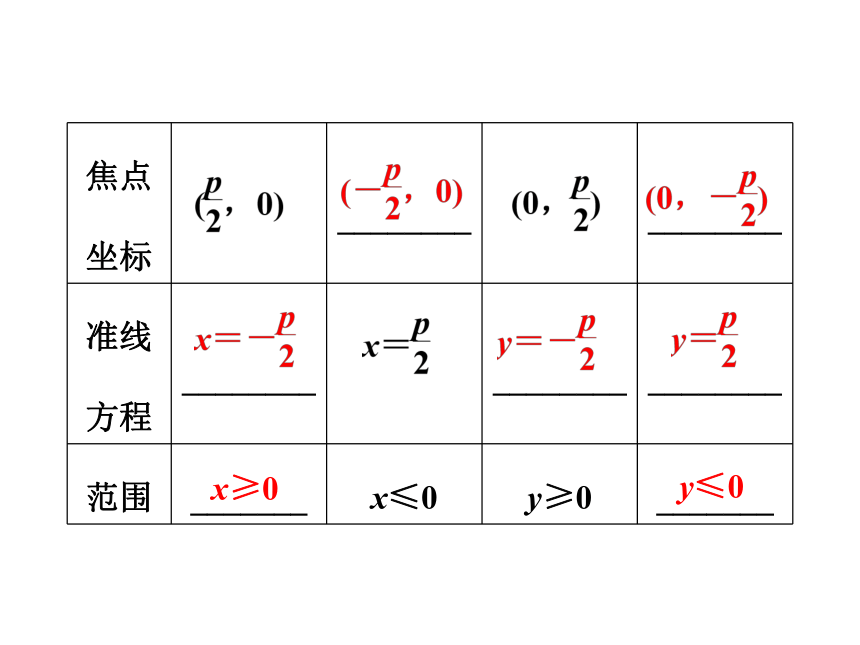
抛物线的几何性质、图形、标准方程列表如下:y2=2px(p>0)x2=-2py(p>0)x≥0y≤0x轴y轴2.焦半径与焦点弦
抛物线上一点与焦点F的连线的线段叫做焦半径,过焦点的直线与抛物线相交所得弦叫做焦点弦,设抛物线上任意一点P(x0,y0),焦点弦端点A(x1,y1),B(x2,y2),则四种标准形式下的焦点弦,焦半径公式为1.抛物线x2=2py(p>0)有几条对称轴?是不是中心对称图形?
提示:有一条对称轴;不是中心对称图形.2.从几何性质上看,抛物线与双曲线有何区别和联系?
提示:(1)抛物线的几何性质和双曲线的几何性质比较起来,差别较大,它的离心率为1,只有一个焦点、一个顶点、一条对称轴、一条准线.它没有对称中心.
(2)抛物线与双曲线的一支,尽管它们都是不封闭的有开口的光滑曲线,但是它们的图象性质是完全不同的.事实上,从开口的变化规律来看,双曲线的开口是越来越大,而抛物线开口越来越趋于扁小.课堂互动讲练抛物线的几何性质应用广泛,如抛物线上点的坐标有范围,求解有关最值问题时,应加以限制;抛物线为轴对称图形,在考虑其内接对称图形时,要注意根据抛物线的对称性确定内接多边形顶点的位置;根据抛物线所满足的几何条件,求抛物线的方程. 正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,求这个正三角形的边长.
【思路点拨】 正三角形的另两个顶点须关于x轴对称,结合对称性设点的坐标进行运算.【名师点评】 解本题的关键是根据抛物线的对称性和正三角形的性质证明A、B两点关于x轴对称.解答本题时要注意不能只凭主观判断而忽视了推理证明的过程.直线与抛物线的位置关系可以类比直线与椭圆的位置关系、直线与双曲线的位置关系,但在直线与抛物线的位置关系中,有一种比较特殊的情况,那就是当直线与抛物线的轴平行或重合时,直线与抛物线相交,但只有一个交点.注意在直线与抛物线的位置关系中,着重讨论直线与抛物线相交的情况.【思路点拨】 由于已知直线过抛物线的焦点,因此可设出直线方程,(1)利用根与系数的关系及弦长公式求解;(2)利用抛物线定义求解.(2)与抛物线过焦点的弦有关的问题,一般的解法是设出直线方程,代入抛物线方程消元后,利用根与系数的关系结合定义求解.自我挑战1 过点Q(4,1)作抛物线y2=8x的弦AB,恰被Q所平分,求AB所在的直线方程.解决定值问题的方法是:先通过设出字母参数,利用该参数将与要求定值的量用有关的某些数学量(比如曲线的方程、点的坐标)表示出来,最后表示要证定值的量与所设参数无关. (本题满分14分)如图,过抛物线y2=x上一点A(4,2)作倾斜角互补的两条直线AB,AC交抛物线于B,C两点,求证:直线BC的斜率是定值.【思路点拨】 由斜率互补,设出AB直线方程,联立方程,求B、C点坐标,求BC的斜率.【名师点评】 在直线和抛物线的综合题中,经常遇到求定值,过定点的问题,解决这类问题的方法有很多,例如斜率法、方程法、向量法、参数法等.解决这类问题的关键是代换和转化.有时利用数形结合思想可以达到避繁就简、化难为易、事半功倍的效果.自我挑战2 A,B为抛物线y2=2px(p>0)上两点,O为原点,若OA⊥OB,求证直线AB过定点.1.抛物线的性质和椭圆、双曲线比较起来,差别较大.它的离心率为1是一个定值,有一个焦点,一个顶点,一条准线,一条对称轴,没有中心,学习中要注意区分,比较记忆.对于抛物线的四种形式的标准方程,应准确把握熟练应用,能作出图形,会利用图形分析性质.当Δ=0时,直线和抛物线相切,有一个公共点;
当Δ<0时,直线和抛物线相离,无公共点.
(2)若k=0,则直线y=b与抛物线y2=2px(p>0)相交,有一个公共点.特别地,当直线l的斜率不存在时,设x=m,则当m>0时,l与抛物线相交,有两个公共点;当m=0时,与抛物线相切,有一个公共点;当m<0时,与抛物线相离,无公共点.知能优化训练本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
1.掌握抛物线的几何性质.
2.会用抛物线的几何性质处理简单问题. 课堂互动讲练知能优化训练2.4.2课前自主学案课前自主学案y2=2px(p>0)x2=2py(p>0)2.抛物线定义的实质是:__________,其中,点F是抛物线的____,dM-l是抛物线上的_______________.
3.过点M(-2,4)的抛物线的标准方程是________________.|MF|=dM-l焦点点到准线的距离x2=y或y2=-8x1.抛物线的几何性质
抛物线的几何性质、图形、标准方程列表如下:y2=2px(p>0)x2=-2py(p>0)x≥0y≤0x轴y轴2.焦半径与焦点弦
抛物线上一点与焦点F的连线的线段叫做焦半径,过焦点的直线与抛物线相交所得弦叫做焦点弦,设抛物线上任意一点P(x0,y0),焦点弦端点A(x1,y1),B(x2,y2),则四种标准形式下的焦点弦,焦半径公式为1.抛物线x2=2py(p>0)有几条对称轴?是不是中心对称图形?
提示:有一条对称轴;不是中心对称图形.2.从几何性质上看,抛物线与双曲线有何区别和联系?
提示:(1)抛物线的几何性质和双曲线的几何性质比较起来,差别较大,它的离心率为1,只有一个焦点、一个顶点、一条对称轴、一条准线.它没有对称中心.
(2)抛物线与双曲线的一支,尽管它们都是不封闭的有开口的光滑曲线,但是它们的图象性质是完全不同的.事实上,从开口的变化规律来看,双曲线的开口是越来越大,而抛物线开口越来越趋于扁小.课堂互动讲练抛物线的几何性质应用广泛,如抛物线上点的坐标有范围,求解有关最值问题时,应加以限制;抛物线为轴对称图形,在考虑其内接对称图形时,要注意根据抛物线的对称性确定内接多边形顶点的位置;根据抛物线所满足的几何条件,求抛物线的方程. 正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,求这个正三角形的边长.
【思路点拨】 正三角形的另两个顶点须关于x轴对称,结合对称性设点的坐标进行运算.【名师点评】 解本题的关键是根据抛物线的对称性和正三角形的性质证明A、B两点关于x轴对称.解答本题时要注意不能只凭主观判断而忽视了推理证明的过程.直线与抛物线的位置关系可以类比直线与椭圆的位置关系、直线与双曲线的位置关系,但在直线与抛物线的位置关系中,有一种比较特殊的情况,那就是当直线与抛物线的轴平行或重合时,直线与抛物线相交,但只有一个交点.注意在直线与抛物线的位置关系中,着重讨论直线与抛物线相交的情况.【思路点拨】 由于已知直线过抛物线的焦点,因此可设出直线方程,(1)利用根与系数的关系及弦长公式求解;(2)利用抛物线定义求解.(2)与抛物线过焦点的弦有关的问题,一般的解法是设出直线方程,代入抛物线方程消元后,利用根与系数的关系结合定义求解.自我挑战1 过点Q(4,1)作抛物线y2=8x的弦AB,恰被Q所平分,求AB所在的直线方程.解决定值问题的方法是:先通过设出字母参数,利用该参数将与要求定值的量用有关的某些数学量(比如曲线的方程、点的坐标)表示出来,最后表示要证定值的量与所设参数无关. (本题满分14分)如图,过抛物线y2=x上一点A(4,2)作倾斜角互补的两条直线AB,AC交抛物线于B,C两点,求证:直线BC的斜率是定值.【思路点拨】 由斜率互补,设出AB直线方程,联立方程,求B、C点坐标,求BC的斜率.【名师点评】 在直线和抛物线的综合题中,经常遇到求定值,过定点的问题,解决这类问题的方法有很多,例如斜率法、方程法、向量法、参数法等.解决这类问题的关键是代换和转化.有时利用数形结合思想可以达到避繁就简、化难为易、事半功倍的效果.自我挑战2 A,B为抛物线y2=2px(p>0)上两点,O为原点,若OA⊥OB,求证直线AB过定点.1.抛物线的性质和椭圆、双曲线比较起来,差别较大.它的离心率为1是一个定值,有一个焦点,一个顶点,一条准线,一条对称轴,没有中心,学习中要注意区分,比较记忆.对于抛物线的四种形式的标准方程,应准确把握熟练应用,能作出图形,会利用图形分析性质.当Δ=0时,直线和抛物线相切,有一个公共点;
当Δ<0时,直线和抛物线相离,无公共点.
(2)若k=0,则直线y=b与抛物线y2=2px(p>0)相交,有一个公共点.特别地,当直线l的斜率不存在时,设x=m,则当m>0时,l与抛物线相交,有两个公共点;当m=0时,与抛物线相切,有一个公共点;当m<0时,与抛物线相离,无公共点.知能优化训练本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
