1.1锐角三角函数 课件(共24张PPT)
文档属性
| 名称 | 1.1锐角三角函数 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 700.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
北师大版九年级下册数学
第一章 直角三角形的边角关系
1.1 锐角三角函数
在距今2500多年前,古希腊数学家就利用相似三角形较准确地测出了埃及大金字塔的高度.
复习回顾
对直角三角形的边角关系,已经研究了什么?还可以研究什么?
答:我们前面研究了直角三角形中角与角之间的关系(两锐角互余)、三边之间的关系(勾股定理),还可以研究边与角之间的关系.
导入新课
从实际需要看,要描述埃及金字塔的倾斜程度,我们需要研究直角三角形中边与角之间的关系:从数学内部看,我们已经研究了直角三角形的边与边的关系、角与角的关系,边与角之间有什么关系呢?本节课我们一起来学习“锐角的三角函数”——锐角的正弦、余弦、正切.
导入新课
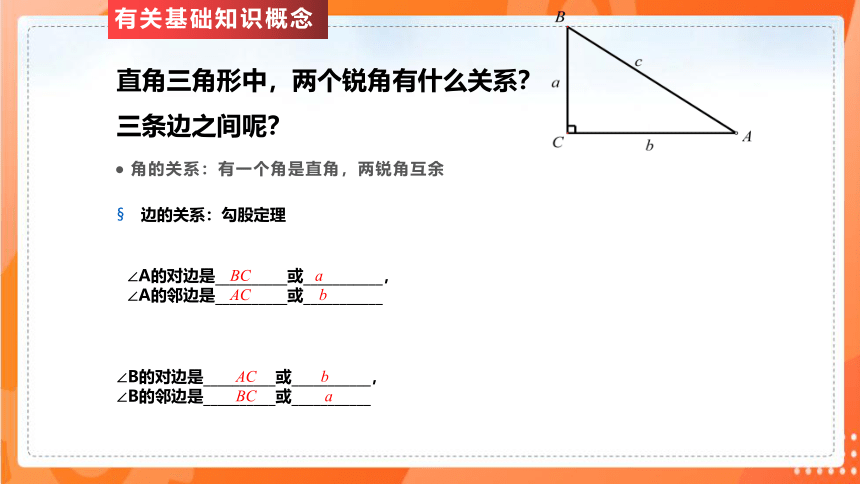
有关基础知识概念
角的关系:有一个角是直角,两锐角互余
边的关系:勾股定理
直角三角形中,两个锐角有什么关系?
三条边之间呢?
∠B的对边是__________或___________,
∠B的邻边是__________或___________
AC b
BC a
∠A的对边是__________或___________,
∠A的邻边是__________或___________
BC a
AC b
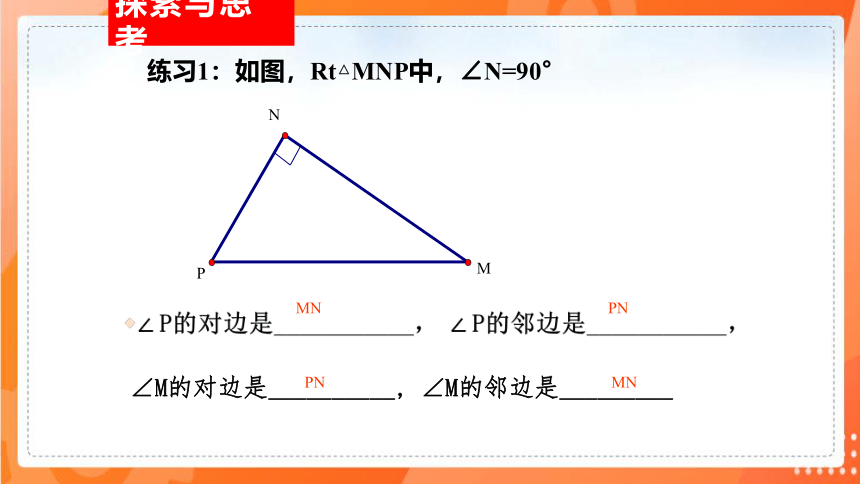
练习1:如图,Rt△MNP中,∠N=90°
N
P
M
探索与思考
MN PN
PN MN
∠M的对边是__________, ∠M的邻边是_________
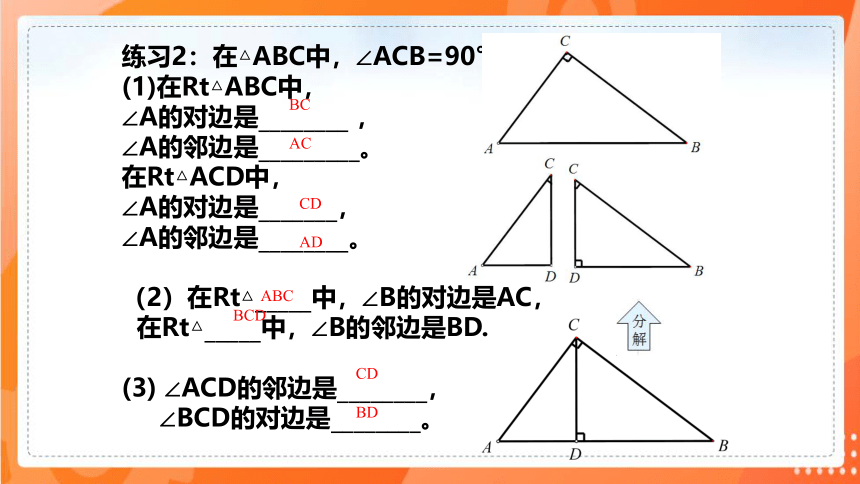
练习2:在△ABC中,∠ACB=90°,CD⊥AB。
(1)在Rt△ABC中,
∠A的对边是________ ,
∠A的邻边是_________。
在Rt△ACD中,
∠A的对边是_______,
∠A的邻边是________。
(2)在Rt△_____中,∠B的对边是AC,
在Rt△_____中,∠B的邻边是BD.
(3) ∠ACD的邻边是________,
∠BCD的对边是________。
BC
AC
CD
AD
ABC
BCD
CD
BD
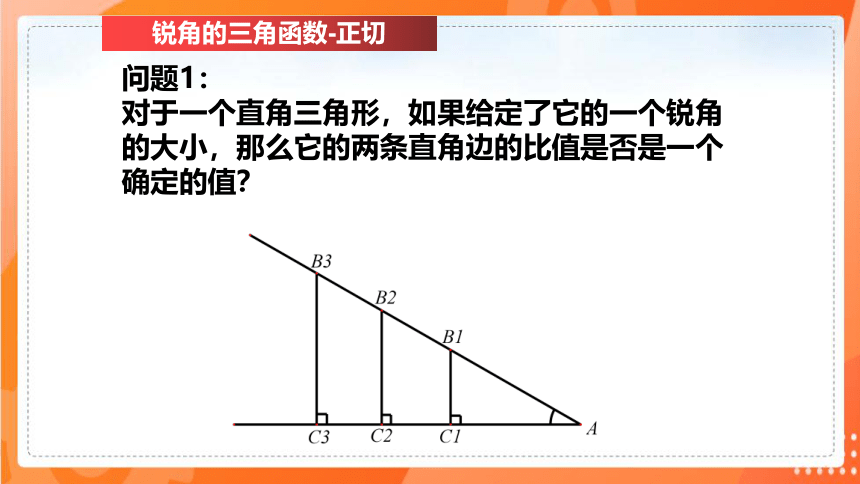
问题1:
对于一个直角三角形,如果给定了它的一个锐角的大小,那么它的两条直角边的比值是否是一个确定的值?
锐角的三角函数-正切
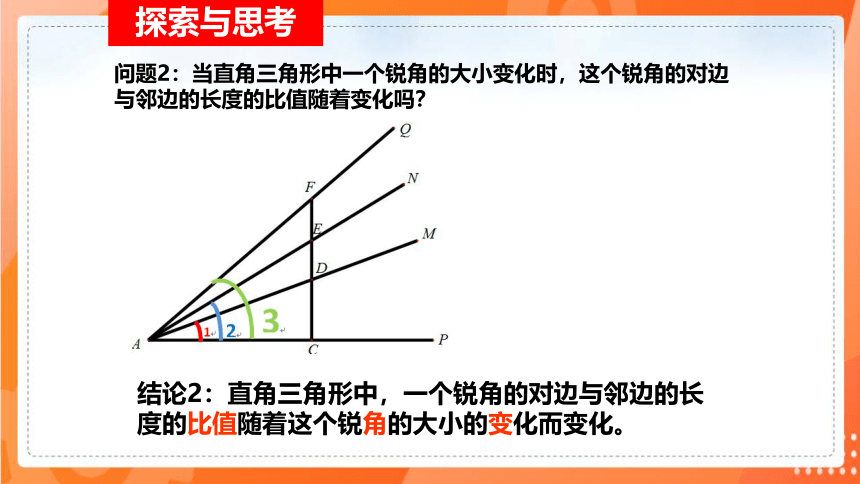
问题2:当直角三角形中一个锐角的大小变化时,这个锐角的对边与邻边的长度的比值随着变化吗?
结论2:直角三角形中,一个锐角的对边与邻边的长度的比值随着这个锐角的大小的变化而变化。
探索与思考
结论2:直角三角形中,一个锐角的对边与邻边的长度的比值随着这个锐角的大小的变化而变化。
结论1:如果给定直角三角形的一个锐角,那么这个锐角的对边与邻边的长度的比值就是一个确定的数。
可以得到:在Rt△ABC中(∠C=90°),当锐角A的大小确定后,不论Rt△ABC的边长怎样变化,∠A的对边BC与邻边AC的比值总是确定的。
我们把直角三角形中一个锐角的对边与邻边的比叫做这个锐角的正切。(tangent)
如图,锐角A的正切记作tanA,这时
正切的应用
(1)梯子的倾斜程度与正切的关系:
如果梯子与地面的夹角为∠A,那么tanA的值_____,梯子
越陡.
(2)坡度:
坡面的_________与_________的比称为坡度(或_____).
越大
铅直高度
水平宽度
坡比
正弦:如图,在Rt△ABC中,∠C=90°,∠A的对
边与斜边的比叫做∠A的正弦,记作sin A,即
sin A=
锐角的三角函数-正弦
例1 如图,在Rt△ABC中,∠B=90°,AC=200,
sinA= 0.6, 求BC的长.
在Rt△ABC中,
∵
即
∴BC=200×0.6=120.
解:
C
把Rt△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定
(中考·贵阳)在Rt△ABC中,∠C=90°,AC=12, BC=5,则sin A的值为( )
A. B. C. D.
如图,P是α的边OA上一点,点P的坐标为(12,5),
则α的正弦值为( )
A. B.
C. D.
余弦:如图,在Rt△ABC中,∠C=90°,∠A的邻
边与斜边的比叫做∠A的余弦,
记作cos A,即cos A=
锐角的三角函数-余弦
要点精析:正弦、余弦的概念是类比正切得到的,其
本质是两条线段的长度之比,没有单位,其大小只与
角的大小有关,与所在的直角三角形无关.
易错警示:(1)“sin A”“cos A”与“tan A”是整体符号,
符号中省去了“∠”.对于用三个大写字母表示的角
来说,如∠AOB,其正弦应写成“sin∠AOB”,而不
能写成“sin AOB”,余弦、正切也是这样的.
(2)(sin A)2应写成sin2 A,而不能写成sin A2.
例2 如图,在Rt△ABC中,
∠C= 90°,AC=12,
BC=5,求sin A,cos A的值.
导引:在Rt△ABC中,已知两直角边长,可先用勾股定理求
斜边长,再利用定义分别求出sin A,cos A的值.
解:∵∠C=90°,AC=12,BC=5,
∴AB=
∴sin A= cos A=
1、如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB、垂足为点D,则(用正切或余切表示).
C
A
B
D
课堂练习
tanB 或 cot∠BCD
tanB 或 cotA
tan∠ACD 或 cot∠CAD
2、如图,△ABC是直角三角形,∠C=90°,D、E在BC上,AC=4,BD=5,DE=2,EC=3,∠ABC=α,∠ADC=β,∠AEC=γ。
求:(1)tanα; (2)tanβ; (3)cotγ
A
g
b
a
D
B
E
C
5
2
3
4
3、如图,在Rt△ABC中,∠C=90°,tanA=2,AC=2,求:BC和AB的值。
2
C
B
A
4、如图,△PQR都是直角三角形,∠R=90°,
PQ=13,PR=5。 求:tanP和cotQ
5
13
P
R
Q
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版九年级下册数学
第一章 直角三角形的边角关系
1.1 锐角三角函数
在距今2500多年前,古希腊数学家就利用相似三角形较准确地测出了埃及大金字塔的高度.
复习回顾
对直角三角形的边角关系,已经研究了什么?还可以研究什么?
答:我们前面研究了直角三角形中角与角之间的关系(两锐角互余)、三边之间的关系(勾股定理),还可以研究边与角之间的关系.
导入新课
从实际需要看,要描述埃及金字塔的倾斜程度,我们需要研究直角三角形中边与角之间的关系:从数学内部看,我们已经研究了直角三角形的边与边的关系、角与角的关系,边与角之间有什么关系呢?本节课我们一起来学习“锐角的三角函数”——锐角的正弦、余弦、正切.
导入新课
有关基础知识概念
角的关系:有一个角是直角,两锐角互余
边的关系:勾股定理
直角三角形中,两个锐角有什么关系?
三条边之间呢?
∠B的对边是__________或___________,
∠B的邻边是__________或___________
AC b
BC a
∠A的对边是__________或___________,
∠A的邻边是__________或___________
BC a
AC b
练习1:如图,Rt△MNP中,∠N=90°
N
P
M
探索与思考
MN PN
PN MN
∠M的对边是__________, ∠M的邻边是_________
练习2:在△ABC中,∠ACB=90°,CD⊥AB。
(1)在Rt△ABC中,
∠A的对边是________ ,
∠A的邻边是_________。
在Rt△ACD中,
∠A的对边是_______,
∠A的邻边是________。
(2)在Rt△_____中,∠B的对边是AC,
在Rt△_____中,∠B的邻边是BD.
(3) ∠ACD的邻边是________,
∠BCD的对边是________。
BC
AC
CD
AD
ABC
BCD
CD
BD
问题1:
对于一个直角三角形,如果给定了它的一个锐角的大小,那么它的两条直角边的比值是否是一个确定的值?
锐角的三角函数-正切
问题2:当直角三角形中一个锐角的大小变化时,这个锐角的对边与邻边的长度的比值随着变化吗?
结论2:直角三角形中,一个锐角的对边与邻边的长度的比值随着这个锐角的大小的变化而变化。
探索与思考
结论2:直角三角形中,一个锐角的对边与邻边的长度的比值随着这个锐角的大小的变化而变化。
结论1:如果给定直角三角形的一个锐角,那么这个锐角的对边与邻边的长度的比值就是一个确定的数。
可以得到:在Rt△ABC中(∠C=90°),当锐角A的大小确定后,不论Rt△ABC的边长怎样变化,∠A的对边BC与邻边AC的比值总是确定的。
我们把直角三角形中一个锐角的对边与邻边的比叫做这个锐角的正切。(tangent)
如图,锐角A的正切记作tanA,这时
正切的应用
(1)梯子的倾斜程度与正切的关系:
如果梯子与地面的夹角为∠A,那么tanA的值_____,梯子
越陡.
(2)坡度:
坡面的_________与_________的比称为坡度(或_____).
越大
铅直高度
水平宽度
坡比
正弦:如图,在Rt△ABC中,∠C=90°,∠A的对
边与斜边的比叫做∠A的正弦,记作sin A,即
sin A=
锐角的三角函数-正弦
例1 如图,在Rt△ABC中,∠B=90°,AC=200,
sinA= 0.6, 求BC的长.
在Rt△ABC中,
∵
即
∴BC=200×0.6=120.
解:
C
把Rt△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定
(中考·贵阳)在Rt△ABC中,∠C=90°,AC=12, BC=5,则sin A的值为( )
A. B. C. D.
如图,P是α的边OA上一点,点P的坐标为(12,5),
则α的正弦值为( )
A. B.
C. D.
余弦:如图,在Rt△ABC中,∠C=90°,∠A的邻
边与斜边的比叫做∠A的余弦,
记作cos A,即cos A=
锐角的三角函数-余弦
要点精析:正弦、余弦的概念是类比正切得到的,其
本质是两条线段的长度之比,没有单位,其大小只与
角的大小有关,与所在的直角三角形无关.
易错警示:(1)“sin A”“cos A”与“tan A”是整体符号,
符号中省去了“∠”.对于用三个大写字母表示的角
来说,如∠AOB,其正弦应写成“sin∠AOB”,而不
能写成“sin AOB”,余弦、正切也是这样的.
(2)(sin A)2应写成sin2 A,而不能写成sin A2.
例2 如图,在Rt△ABC中,
∠C= 90°,AC=12,
BC=5,求sin A,cos A的值.
导引:在Rt△ABC中,已知两直角边长,可先用勾股定理求
斜边长,再利用定义分别求出sin A,cos A的值.
解:∵∠C=90°,AC=12,BC=5,
∴AB=
∴sin A= cos A=
1、如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB、垂足为点D,则(用正切或余切表示).
C
A
B
D
课堂练习
tanB 或 cot∠BCD
tanB 或 cotA
tan∠ACD 或 cot∠CAD
2、如图,△ABC是直角三角形,∠C=90°,D、E在BC上,AC=4,BD=5,DE=2,EC=3,∠ABC=α,∠ADC=β,∠AEC=γ。
求:(1)tanα; (2)tanβ; (3)cotγ
A
g
b
a
D
B
E
C
5
2
3
4
3、如图,在Rt△ABC中,∠C=90°,tanA=2,AC=2,求:BC和AB的值。
2
C
B
A
4、如图,△PQR都是直角三角形,∠R=90°,
PQ=13,PR=5。 求:tanP和cotQ
5
13
P
R
Q
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
