1.230°,45°,60°角的三角函数值 课件(共22张PPT)
文档属性
| 名称 | 1.230°,45°,60°角的三角函数值 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 677.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 10:50:04 | ||
图片预览





文档简介
(共22张PPT)
北师大版九年级下册数学
第一章 直角三角形的边角关系
1.2 30°,45°,60°角的三角函数值
2.在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
直角三角形中边与角的关系:锐角三角函数.
b
A
B
C
a
┌
c
3.sin A和cos B, cos A和sin B有什么关系
sin A=cos B, cos A=sin B.
1.锐角三角函数的定义:
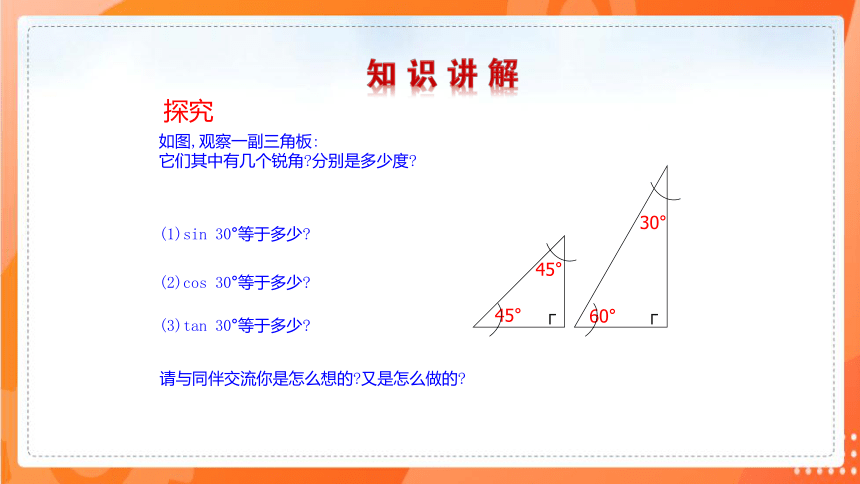
如图,观察一副三角板:
它们其中有几个锐角 分别是多少度
(1)sin 30°等于多少
┌
┌
30°
60°
45°
45°
(2)cos 30°等于多少
(3)tan 30°等于多少
请与同伴交流你是怎么想的 又是怎么做的
探究
(4)sin 45°,sin 60°等于多少
(5)cos 45°,cos 60°等于多少
(6)tan 45°,tan 60°等于多少
┌
┌
30°
60°
45°
45°
根据上面的计算,完成下表:<特殊角的三角函数值表>
老师期望:
你能对伴随你学生生涯的这副三角板所具有的功能进行重新认识和评价吗?
在Rt△ABC中,∠C=90°, ∠A=45° .设AC=1。
1
1
2
AB=
.
BC
AC
2
1
1
2
2
2
2
=
+
=
+
sin45°=
;
AB
BC
2
2
2
1
=
=
cos45°=
;
AB
AC
2
2
2
1
=
=
tan45°=
.
AC
BC
1
1
1
=
=
sin45°,cos45 °,tan45 °的值分别是多少?
BC=AC=1.
A
B
C
(
45°
30°
A
B
C
x
2x
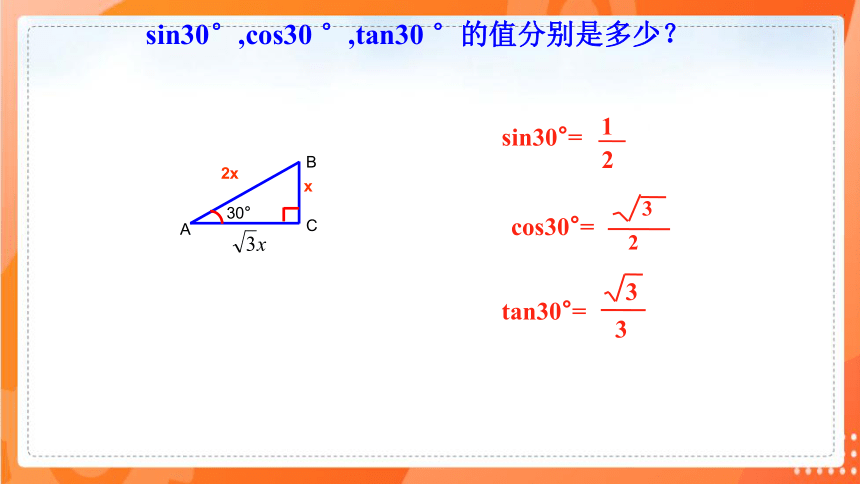
sin30°=
2
1
cos30°=
2
3
tan30°=
3
3
sin30°,cos30 °,tan30 °的值分别是多少?
60°
A
B
C
x
2x
30°
sin60°=
2
3
cos60 °=
2
1
tan60 °=
3
sin60°,cos60 °,tan60 °的值分别是多少?
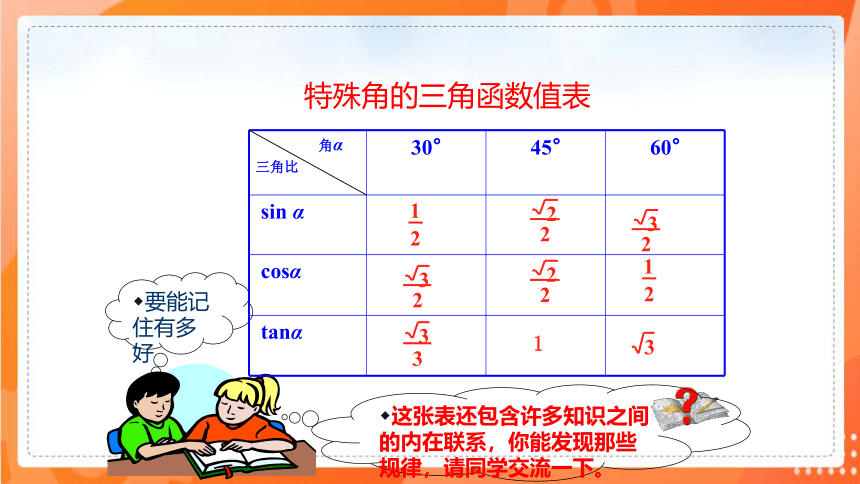
特殊角的三角函数值表
要能记住有多好
这张表还包含许多知识之间的内在联系,你能发现那些规律,请同学交流一下。
角α 三角比 30° 45° 60°
sin α
cosα
tanα
1
2
1
2
2
2
3
3
2
1
2
3
2
2
3
3
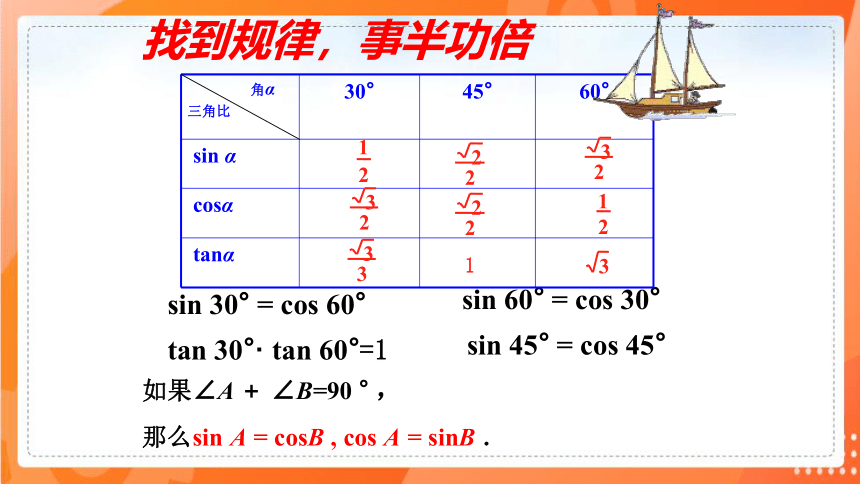
sin 30° = cos 60°
sin 60° = cos 30°
tan 30°· tan 60°=1
sin 45° = cos 45°
如果∠A + ∠B=90 ° ,
那么sin A = cosB , cos A = sinB .
角α 三角比 30° 45° 60°
sin α
cosα
tanα
1
2
1
2
2
2
3
3
2
1
2
3
2
2
3
3
找到规律,事半功倍
例 计算:
(1)sin 30°+cos 45°.
(2)sin2 60°+cos2 60°-tan 45°.
老师提示:
sin260°表示(sin60°)2,
cos260°表示(cos60°)2,其余类推.
解:(1)sin 30°+cos 45°
(2) sin260°+cos260°-tan45°
【一题多变】
用计算器计算cos 10°,cos 20°,cos 30°,…,
cos 90°的值,总结规律,并利用此规律比较当
0°<α<β<90°时,cos α与cos β的大小,即
cos α______cos β.
>
【母题变式】
【变式一】(变换条件)先用计算器求:sin 20°≈
__________,sin 40°≈____________,sin 60°≈
__________,sin 80°≈___________,再按从小到大的顺
序用“<”把sin 20°,sin 40°,sin 60°,sin 80°
连接起来:______________________________________.
归纳:在锐角范围内,正弦值,角大值 _____.
0.342 0
0.642 8
0.866 0
0.984 8
sin 20°大
1.(黄冈·中考)cos30°=( )
A.
B.
D.
【解析】选C.由三角函数的定义知cos30°=
C.
课堂练习
sin45°的结果等于( )
2.(荆门·中考)计算
【解析】选B.
B.1 C.
D.
A.
3.(眉山·中考)如图,已知在梯形ABCD中,AD∥BC,
∠B=30°,∠C=60°,AD=4,AB= ,
则下底BC的长为 __________.
【解析】10
4.(丹东·中考)计算:
【解析】
.
=2.
5.(巴中·中考)已知,如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
(1)求cos∠ACB的值.
(2)若E,F分别是AB,DC的中点,连接EF,求线段EF的长.
C
D
B
A
cos∠ACB=cos 30°= .
∴EF=
=12.
【解析】(1)∵∠B=60°,
∴∠BCD=60°,又
∵AB=AD=DC,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠DCA=∠BCA.
∴∠ACB=30°.
(2)∵AB=AD=DC=8,∠ACB=30°,∴BC=2AB=16,
∵E,F分别是AB,DC的中点,
【规律方法】
1.记住30°,45 °,60 °角的三角函数值及推导方式,可以提高计算速度.
2.会构造直角三角形,充分利用勾股定理的有关知识结合三角函数灵活运用.
直角三角形三边的关系.
直角三角形两锐角的关系.
直角三角形边与角之间的关系.
特殊角30°,45°,60°角的三角函数值.
互余两角之间的三角函数关系.
同角之间的三角函数关系
b
A
B
C
a
┌
c
┌
┌
30°
60°
45°
45°
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版九年级下册数学
第一章 直角三角形的边角关系
1.2 30°,45°,60°角的三角函数值
2.在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
直角三角形中边与角的关系:锐角三角函数.
b
A
B
C
a
┌
c
3.sin A和cos B, cos A和sin B有什么关系
sin A=cos B, cos A=sin B.
1.锐角三角函数的定义:
如图,观察一副三角板:
它们其中有几个锐角 分别是多少度
(1)sin 30°等于多少
┌
┌
30°
60°
45°
45°
(2)cos 30°等于多少
(3)tan 30°等于多少
请与同伴交流你是怎么想的 又是怎么做的
探究
(4)sin 45°,sin 60°等于多少
(5)cos 45°,cos 60°等于多少
(6)tan 45°,tan 60°等于多少
┌
┌
30°
60°
45°
45°
根据上面的计算,完成下表:<特殊角的三角函数值表>
老师期望:
你能对伴随你学生生涯的这副三角板所具有的功能进行重新认识和评价吗?
在Rt△ABC中,∠C=90°, ∠A=45° .设AC=1。
1
1
2
AB=
.
BC
AC
2
1
1
2
2
2
2
=
+
=
+
sin45°=
;
AB
BC
2
2
2
1
=
=
cos45°=
;
AB
AC
2
2
2
1
=
=
tan45°=
.
AC
BC
1
1
1
=
=
sin45°,cos45 °,tan45 °的值分别是多少?
BC=AC=1.
A
B
C
(
45°
30°
A
B
C
x
2x
sin30°=
2
1
cos30°=
2
3
tan30°=
3
3
sin30°,cos30 °,tan30 °的值分别是多少?
60°
A
B
C
x
2x
30°
sin60°=
2
3
cos60 °=
2
1
tan60 °=
3
sin60°,cos60 °,tan60 °的值分别是多少?
特殊角的三角函数值表
要能记住有多好
这张表还包含许多知识之间的内在联系,你能发现那些规律,请同学交流一下。
角α 三角比 30° 45° 60°
sin α
cosα
tanα
1
2
1
2
2
2
3
3
2
1
2
3
2
2
3
3
sin 30° = cos 60°
sin 60° = cos 30°
tan 30°· tan 60°=1
sin 45° = cos 45°
如果∠A + ∠B=90 ° ,
那么sin A = cosB , cos A = sinB .
角α 三角比 30° 45° 60°
sin α
cosα
tanα
1
2
1
2
2
2
3
3
2
1
2
3
2
2
3
3
找到规律,事半功倍
例 计算:
(1)sin 30°+cos 45°.
(2)sin2 60°+cos2 60°-tan 45°.
老师提示:
sin260°表示(sin60°)2,
cos260°表示(cos60°)2,其余类推.
解:(1)sin 30°+cos 45°
(2) sin260°+cos260°-tan45°
【一题多变】
用计算器计算cos 10°,cos 20°,cos 30°,…,
cos 90°的值,总结规律,并利用此规律比较当
0°<α<β<90°时,cos α与cos β的大小,即
cos α______cos β.
>
【母题变式】
【变式一】(变换条件)先用计算器求:sin 20°≈
__________,sin 40°≈____________,sin 60°≈
__________,sin 80°≈___________,再按从小到大的顺
序用“<”把sin 20°,sin 40°,sin 60°,sin 80°
连接起来:______________________________________.
归纳:在锐角范围内,正弦值,角大值 _____.
0.342 0
0.642 8
0.866 0
0.984 8
sin 20°
1.(黄冈·中考)cos30°=( )
A.
B.
D.
【解析】选C.由三角函数的定义知cos30°=
C.
课堂练习
sin45°的结果等于( )
2.(荆门·中考)计算
【解析】选B.
B.1 C.
D.
A.
3.(眉山·中考)如图,已知在梯形ABCD中,AD∥BC,
∠B=30°,∠C=60°,AD=4,AB= ,
则下底BC的长为 __________.
【解析】10
4.(丹东·中考)计算:
【解析】
.
=2.
5.(巴中·中考)已知,如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
(1)求cos∠ACB的值.
(2)若E,F分别是AB,DC的中点,连接EF,求线段EF的长.
C
D
B
A
cos∠ACB=cos 30°= .
∴EF=
=12.
【解析】(1)∵∠B=60°,
∴∠BCD=60°,又
∵AB=AD=DC,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠DCA=∠BCA.
∴∠ACB=30°.
(2)∵AB=AD=DC=8,∠ACB=30°,∴BC=2AB=16,
∵E,F分别是AB,DC的中点,
【规律方法】
1.记住30°,45 °,60 °角的三角函数值及推导方式,可以提高计算速度.
2.会构造直角三角形,充分利用勾股定理的有关知识结合三角函数灵活运用.
直角三角形三边的关系.
直角三角形两锐角的关系.
直角三角形边与角之间的关系.
特殊角30°,45°,60°角的三角函数值.
互余两角之间的三角函数关系.
同角之间的三角函数关系
b
A
B
C
a
┌
c
┌
┌
30°
60°
45°
45°
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
