1.5-1.6三角函数的应用利用三角函数测高 课件(共47张PPT)
文档属性
| 名称 | 1.5-1.6三角函数的应用利用三角函数测高 课件(共47张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 10:47:48 | ||
图片预览





文档简介
(共47张PPT)
北师大版九年级下册数学
第一章 直角三角形的边角关系
1.5-1.6 三角函数的应用 利用三角函数测高
我们已经知道轮船在海中航行时,可以用方位角准确描述它的航行方向.
那你知道如何结合方位角等数据进行计算,帮助轮船在航行中远离危险吗?
情景引入
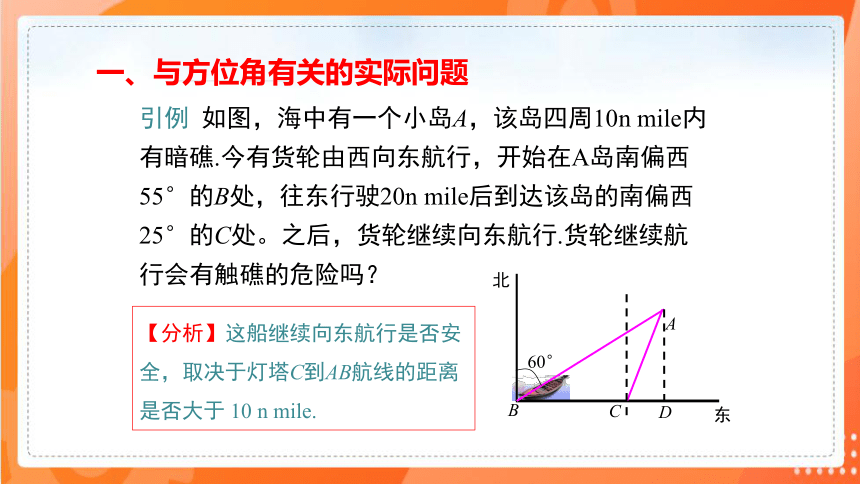
引例 如图,海中有一个小岛A,该岛四周10n mile内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20n mile后到达该岛的南偏西25°的C处。之后,货轮继续向东航行.货轮继续航行会有触礁的危险吗?
B
A
C
60°
一、与方位角有关的实际问题
D
【分析】这船继续向东航行是否安全,取决于灯塔C到AB航线的距离是否大于 10 n mile.
北
东
解:由点A作AD⊥BC于点D,
设AD= x ,
则在Rt△ABD中,
在Rt△ACD中,
解得
所以,这船继续向东航行是安全的.
B
A
C
D
25°
55°
北
东
由BC=BD-CD,得
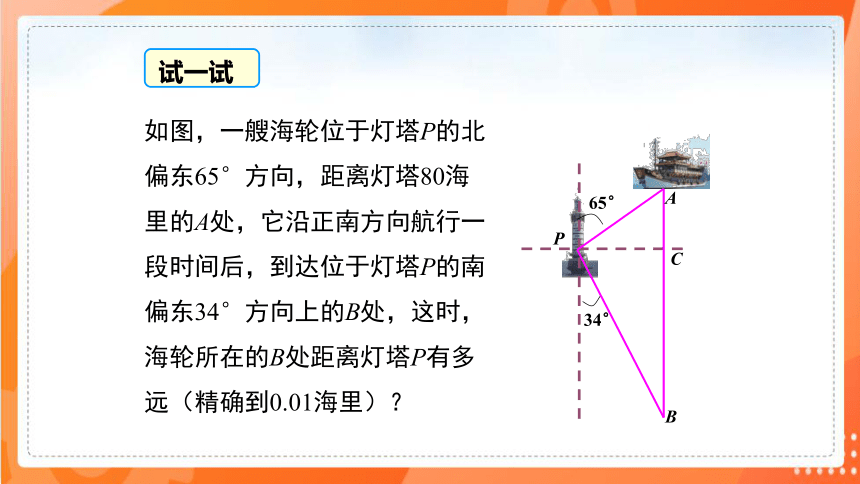
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01海里)?
65°
34°
P
B
C
A
试一试
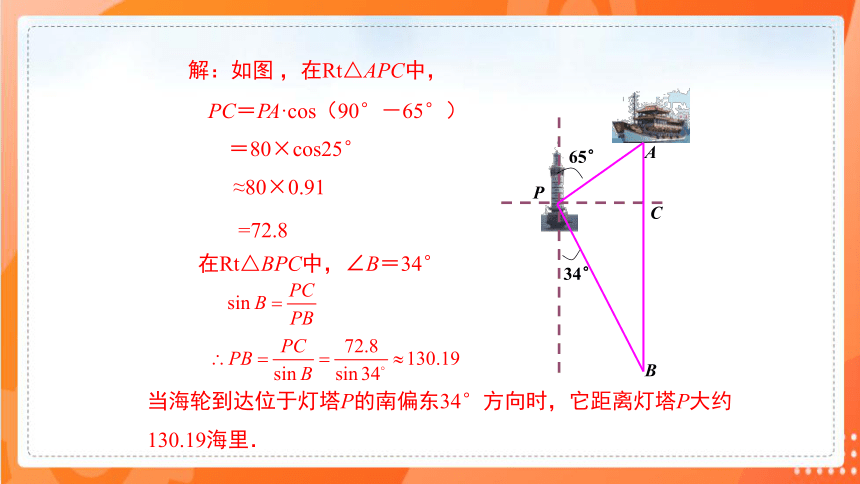
解:如图 ,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈80×0.91
=72.8
在Rt△BPC中,∠B=34°
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130.19海里.
65°
34°
P
B
C
A
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
方法归纳
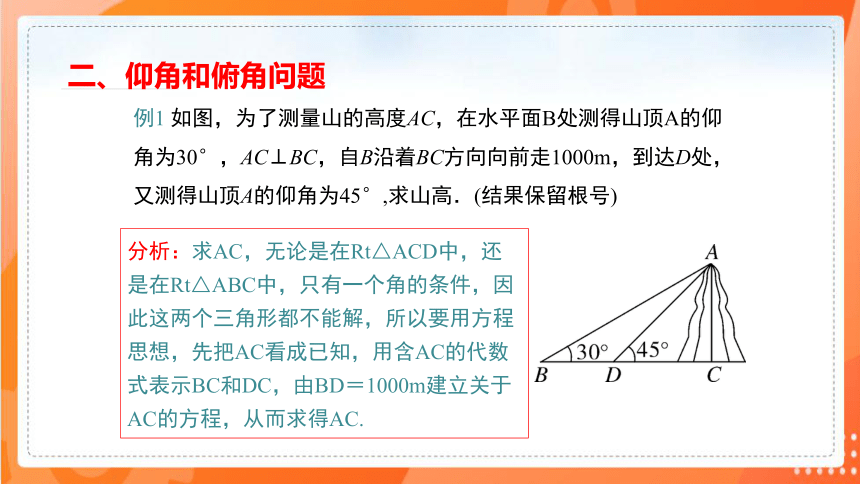
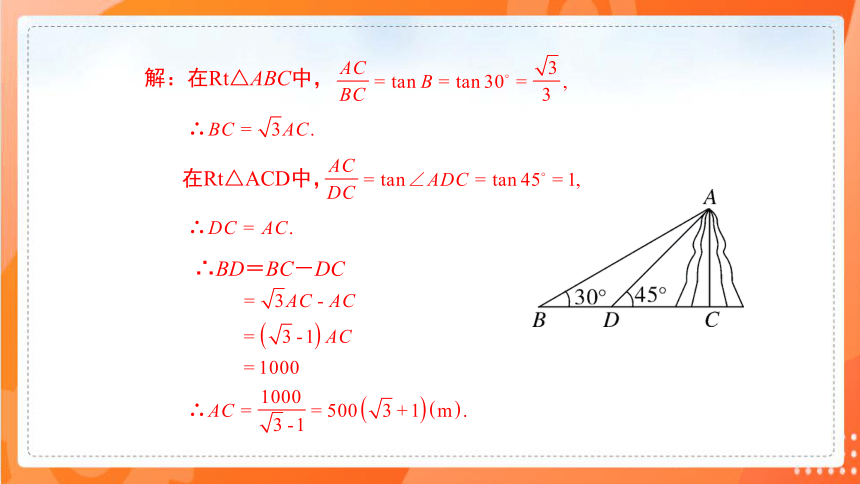
例1 如图,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,AC⊥BC,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,求山高.(结果保留根号)
分析:求AC,无论是在Rt△ACD中,还是在Rt△ABC中,只有一个角的条件,因此这两个三角形都不能解,所以要用方程思想,先把AC看成已知,用含AC的代数式表示BC和DC,由BD=1000m建立关于AC的方程,从而求得AC.
二、仰角和俯角问题
解:在Rt△ABC中,
在Rt△ACD中,
∴BD=BC-DC
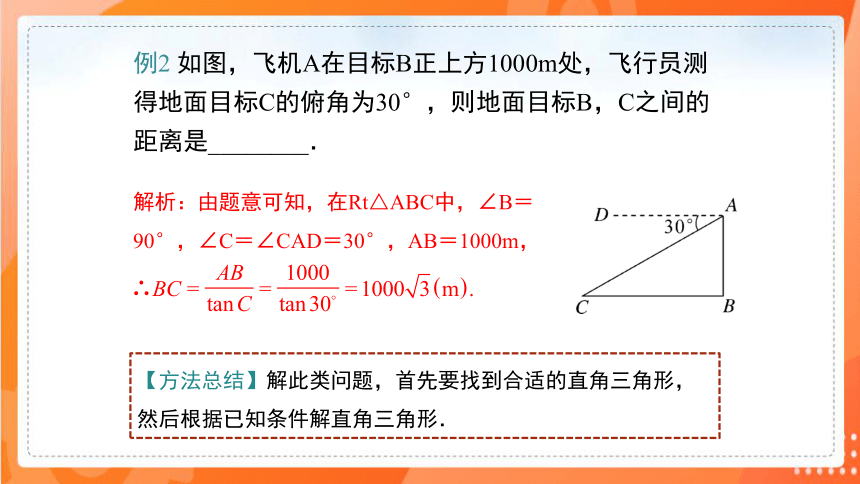
例2 如图,飞机A在目标B正上方1000m处,飞行员测得地面目标C的俯角为30°,则地面目标B,C之间的距离是________.
解析:由题意可知,在Rt△ABC中,∠B=90°,∠C=∠CAD=30°,AB=1000m,
【方法总结】解此类问题,首先要找到合适的直角三角形,然后根据已知条件解直角三角形.
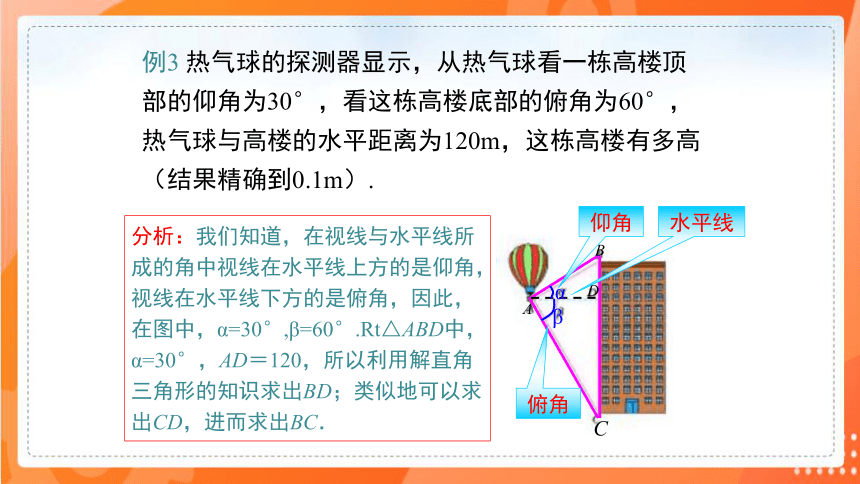
例3 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°.Rt△ABD中,
α=30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
A
B
C
D
α
β
仰角
水平线
俯角
解:如图,α = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
A
B
C
D
α
β
建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
A
B
C
D
40m
54°
45°
A
B
C
D
40m
54°
45°
解:在等腰三角形BCD中∠ACD=90°,
BC=DC=40m.
在Rt△ACD中,
∴AB=AC-BC=55.2-40=15.1
答:旗杆的高度为15.1m.
练一练
三、利用坡角解决实际问题
例4 一段路基的横断面是梯形,高为4米,上底的宽是12米,路基的坡面与地面的倾角分别是45°和30°,求路基下底的宽(精确到0.1米, ).
45°
30°
4米
12米
A
B
C
D
解:作DE⊥AB,CF⊥AB,垂足分别为E、F.由题意可知
DE=CF=4(米),
CD=EF=12(米).
在Rt△ADE中,
在Rt△BCF中,同理可得
因此AB=AE+EF+BF=4+12+6.93≈22.93(米).
答: 路基下底的宽约为22.93米.
45°
30°
4米
12米
A
B
C
E
F
D
北师大版 九年级上册数学
第一章 直角三角形的边角关系
1.6 利用三角函数测高
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
活动一:
测量倾斜角(仰角或俯角).
测量倾斜角可以用测倾器,简单的测倾器由度盘、铅锤和支杆组成(如图).
讲授新课
30°
0°
60°
90°
90°
60°
30°
30°
0°
60°
90°
90°
60°
30°
水平线
活动一:测量倾斜角
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
M
议一议
根据刚才测量数据,你能求出目标M的仰角或俯角吗?说说你的理由.
1
2
3
4
30°
0°
60°
90°
90°
60°
30°
水平线
哈哈:同角的余角相等
M
活动一:测量倾斜角
活动二:
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体底部之间的距离.
如图,要测量物体MN的高度,需测量哪些数据?
1.在测点A处安置测倾器,
测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=L.
3.量出测倾器的高度AC=a
C
A
E
N
M
a
L
α
可按下列步骤进行:
测量底部可以到达的物体的高度
a
C
A
E
N
M
L
α
根据刚才测量的数据,你能求出物体MN的高度吗 说说你的理由.
和同伴交流一下,你发现了什么?
在Rt△MCE中,
ME=EC tanα=AN tanα=L tanα
MN=ME+EN=ME+AC=L tanα+a
MN=Ltanα+ a
L=20.06m
L=19.97m
L=20.15m
AN的长L
a=1.22m
a=1.21 m
a=1.23m
测倾器高a
α=30°2 ′
α=29°49 ′
α=30°15′
倾斜角α
平均值
第二次
第一次
测量项目
测量学校旗杆MN的高度(底部可以到达)
课题
测
量
示
意
图
测
得
数
据
计
算
过
程
感
受
C
a
A
N
E
M
α
L
在Rt△MCE中,ME = ECtanα=ANtanα=20.6×tan30°2′≈
20.6×0.578=11.60m,MN=ME+EN=ME+AC=11.60+1.22
=12.82m
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体底部之间的距离.(如图)
要测量物体MN的高度,使用侧倾器测一次仰角够吗?为什么?
a
α
E
C
A
N
M
活动三:测量底部不可以到达的物体的高度
要测量物体MN的高度,测一次仰角是不够的.
a
b
α
E
C
A
D
B
β
N
M
还需哪些条件,测量哪些数据呢?
活动三:测量底部不可以到达的物体的高度
a
b
α
E
C
A
D
B
β
N
M
如图,要测量物体MN的高度,可以按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾(A,B与N在一条直线上),测得M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
根据测量数据,你能求出物体MN的高度吗 说说你的理由.
根据测量数据,物体MN的高度计算过程:
a
b
α
E
C
A
D
B
β
N
M
在Rt△MDE中,
ED=
在Rt△MCE中,
EC =
EC-ED= - =b
课题 在平面上测量某大厦的高AB 测量示意图 测得数据 测量项目 ∠α ∠β CD的长
第一次 30° 16′ 44° 35′ 60.11m
第二次 29° 44′ 45° 25′ 59.89m
平均值
下表是小明所填实习报告的部分内容:
C
E
D
F
A
G
B
α
β
学以致用:
加油,你是最棒的!
1.请根据小明测得的数据,填写表中的空格;
2.已知测倾器的高CE=DF=1m,通过计算求得,该大厦的高为______m (精确到1m).
答:30°, 45°, 60m
解:在Rt△AEG中,
EG= =1.732AG
在Rt△AFG中,FG=
EG-FG=C D
1.732AG-AG=60
AG=60÷0.732≈81.96
AB=AG+1≈83(m)
做一做
83
大家要认真思考哦
与同伴交流一下,谈谈你的想法?
(1)到目前为止,你有哪些测量物体高度的方法?
(2)如果一个物体的高度已知或容易测量,那么如何测量某测点到该物体的水平距离?
议一议
相信你能行!
活动与探究:
如图,山上有一座铁塔,山脚下有一矩形建筑物ABCD.且建筑物周围没有开阔平整地带.该建筑物顶端宽度AD和高度DC都可以直接测得。从A、D、C三点可看到塔顶端H.可供使用的测员工具有皮尺,测倾器(即测角仪).
(1)请你根据现有条件,充分利用矩形建筑物.设计一个测量塔顶端到地面高度HG的方案.具体要求如下:
①测量数据尽可能少;
②在所给图形上,画出你设计的测量的平面图,并将应测数据标记在图形上(如果测A、D间距离,用m表示;如果测D、C间距离,用n表示;如果测角,用α、β、γ等表示.测倾器高度不计)
(2)根据你测量的数据,计算塔顶到地面的高度HG(用字母I表示)
方案一
(1)如图(a)(测四个数据)
AD=m,CD=n,∠HDM= ,∠HAM=β
(2)设HG=x,HM=x-n,
在Rt△HDM中,tan = ,DM=
在Rt△HAM中,tanβ= ,DM=
∵AM-DM=AD,
∴ - =m,
x= +n.
方案二
(1)如图(b)(测三个数据)
CD=n,∠HDM=α,∠HCG=γ.
(2)设HG=x,HM=x-n,
在Rt△CHG中,tanγ= ,CG= ,
在Rt△HDM中,tanα = ,DM= ,
∵CG=DM,
∴ = ,x=
1.如图,有一斜坡AB长40m,坡顶离地面的
高度为20m,求此斜坡的倾斜角.
A
C
B
解:如图∠C=90°,AB=40, BC=20
∴sin∠A=
∴∠A=30°
课堂练习
2. 水库大坝的截面是梯形ABCD,其中AD∥BC,坝顶AD=6m,
坡长CD=8m,坡底BC=30m,∠ADC=135°.
(1)求坡角∠ABC的大小;
(2)如果坝长100m,那么修建这个大坝共需多少土石料
(结果精确到0.01m3).
A
D
B
C
A
D
B
C
F
E
解:(1)如图,作AE⊥BC,DF⊥BC
则∠FDC=135°-90°=45°
∴AE=DF=FC=CDsin45°=
∴BE=BC-FC-EF=BC-FC-AD=24-
∴tan∠ABC=
∴∠ABC≈17°8′21″
A
D
B
C
F
E
解:(2)S梯形ABCD=(6+30)× ÷2= (m2)
V=100×S梯形ABCD=100× ≈10182.34(m3)
建筑大坝共需10182.34m3的土石.
图K-7-3
B
图K-7-4
B
[解析] B 先根据CD=20 m,DE=10 m得出∠DCE=30°,故可得出∠DCB=90°,再由∠BDF=30°可知∠DBF=60°,由DF∥AE可得出∠BGF=∠BCA=60°,故∠GBF=30°,所以∠DBC=30°,再由锐角三角函数的定义即可得出结论.
图K-7-5
A
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
(5)学会使用了测角仪
(6)研讨了测量可到达底部和不可以到达底部的物体高度的方案.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版九年级下册数学
第一章 直角三角形的边角关系
1.5-1.6 三角函数的应用 利用三角函数测高
我们已经知道轮船在海中航行时,可以用方位角准确描述它的航行方向.
那你知道如何结合方位角等数据进行计算,帮助轮船在航行中远离危险吗?
情景引入
引例 如图,海中有一个小岛A,该岛四周10n mile内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20n mile后到达该岛的南偏西25°的C处。之后,货轮继续向东航行.货轮继续航行会有触礁的危险吗?
B
A
C
60°
一、与方位角有关的实际问题
D
【分析】这船继续向东航行是否安全,取决于灯塔C到AB航线的距离是否大于 10 n mile.
北
东
解:由点A作AD⊥BC于点D,
设AD= x ,
则在Rt△ABD中,
在Rt△ACD中,
解得
所以,这船继续向东航行是安全的.
B
A
C
D
25°
55°
北
东
由BC=BD-CD,得
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01海里)?
65°
34°
P
B
C
A
试一试
解:如图 ,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈80×0.91
=72.8
在Rt△BPC中,∠B=34°
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130.19海里.
65°
34°
P
B
C
A
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
方法归纳
例1 如图,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,AC⊥BC,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,求山高.(结果保留根号)
分析:求AC,无论是在Rt△ACD中,还是在Rt△ABC中,只有一个角的条件,因此这两个三角形都不能解,所以要用方程思想,先把AC看成已知,用含AC的代数式表示BC和DC,由BD=1000m建立关于AC的方程,从而求得AC.
二、仰角和俯角问题
解:在Rt△ABC中,
在Rt△ACD中,
∴BD=BC-DC
例2 如图,飞机A在目标B正上方1000m处,飞行员测得地面目标C的俯角为30°,则地面目标B,C之间的距离是________.
解析:由题意可知,在Rt△ABC中,∠B=90°,∠C=∠CAD=30°,AB=1000m,
【方法总结】解此类问题,首先要找到合适的直角三角形,然后根据已知条件解直角三角形.
例3 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°.Rt△ABD中,
α=30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
A
B
C
D
α
β
仰角
水平线
俯角
解:如图,α = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
A
B
C
D
α
β
建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
A
B
C
D
40m
54°
45°
A
B
C
D
40m
54°
45°
解:在等腰三角形BCD中∠ACD=90°,
BC=DC=40m.
在Rt△ACD中,
∴AB=AC-BC=55.2-40=15.1
答:旗杆的高度为15.1m.
练一练
三、利用坡角解决实际问题
例4 一段路基的横断面是梯形,高为4米,上底的宽是12米,路基的坡面与地面的倾角分别是45°和30°,求路基下底的宽(精确到0.1米, ).
45°
30°
4米
12米
A
B
C
D
解:作DE⊥AB,CF⊥AB,垂足分别为E、F.由题意可知
DE=CF=4(米),
CD=EF=12(米).
在Rt△ADE中,
在Rt△BCF中,同理可得
因此AB=AE+EF+BF=4+12+6.93≈22.93(米).
答: 路基下底的宽约为22.93米.
45°
30°
4米
12米
A
B
C
E
F
D
北师大版 九年级上册数学
第一章 直角三角形的边角关系
1.6 利用三角函数测高
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
活动一:
测量倾斜角(仰角或俯角).
测量倾斜角可以用测倾器,简单的测倾器由度盘、铅锤和支杆组成(如图).
讲授新课
30°
0°
60°
90°
90°
60°
30°
30°
0°
60°
90°
90°
60°
30°
水平线
活动一:测量倾斜角
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
M
议一议
根据刚才测量数据,你能求出目标M的仰角或俯角吗?说说你的理由.
1
2
3
4
30°
0°
60°
90°
90°
60°
30°
水平线
哈哈:同角的余角相等
M
活动一:测量倾斜角
活动二:
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体底部之间的距离.
如图,要测量物体MN的高度,需测量哪些数据?
1.在测点A处安置测倾器,
测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=L.
3.量出测倾器的高度AC=a
C
A
E
N
M
a
L
α
可按下列步骤进行:
测量底部可以到达的物体的高度
a
C
A
E
N
M
L
α
根据刚才测量的数据,你能求出物体MN的高度吗 说说你的理由.
和同伴交流一下,你发现了什么?
在Rt△MCE中,
ME=EC tanα=AN tanα=L tanα
MN=ME+EN=ME+AC=L tanα+a
MN=Ltanα+ a
L=20.06m
L=19.97m
L=20.15m
AN的长L
a=1.22m
a=1.21 m
a=1.23m
测倾器高a
α=30°2 ′
α=29°49 ′
α=30°15′
倾斜角α
平均值
第二次
第一次
测量项目
测量学校旗杆MN的高度(底部可以到达)
课题
测
量
示
意
图
测
得
数
据
计
算
过
程
感
受
C
a
A
N
E
M
α
L
在Rt△MCE中,ME = ECtanα=ANtanα=20.6×tan30°2′≈
20.6×0.578=11.60m,MN=ME+EN=ME+AC=11.60+1.22
=12.82m
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体底部之间的距离.(如图)
要测量物体MN的高度,使用侧倾器测一次仰角够吗?为什么?
a
α
E
C
A
N
M
活动三:测量底部不可以到达的物体的高度
要测量物体MN的高度,测一次仰角是不够的.
a
b
α
E
C
A
D
B
β
N
M
还需哪些条件,测量哪些数据呢?
活动三:测量底部不可以到达的物体的高度
a
b
α
E
C
A
D
B
β
N
M
如图,要测量物体MN的高度,可以按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾(A,B与N在一条直线上),测得M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
根据测量数据,你能求出物体MN的高度吗 说说你的理由.
根据测量数据,物体MN的高度计算过程:
a
b
α
E
C
A
D
B
β
N
M
在Rt△MDE中,
ED=
在Rt△MCE中,
EC =
EC-ED= - =b
课题 在平面上测量某大厦的高AB 测量示意图 测得数据 测量项目 ∠α ∠β CD的长
第一次 30° 16′ 44° 35′ 60.11m
第二次 29° 44′ 45° 25′ 59.89m
平均值
下表是小明所填实习报告的部分内容:
C
E
D
F
A
G
B
α
β
学以致用:
加油,你是最棒的!
1.请根据小明测得的数据,填写表中的空格;
2.已知测倾器的高CE=DF=1m,通过计算求得,该大厦的高为______m (精确到1m).
答:30°, 45°, 60m
解:在Rt△AEG中,
EG= =1.732AG
在Rt△AFG中,FG=
EG-FG=C D
1.732AG-AG=60
AG=60÷0.732≈81.96
AB=AG+1≈83(m)
做一做
83
大家要认真思考哦
与同伴交流一下,谈谈你的想法?
(1)到目前为止,你有哪些测量物体高度的方法?
(2)如果一个物体的高度已知或容易测量,那么如何测量某测点到该物体的水平距离?
议一议
相信你能行!
活动与探究:
如图,山上有一座铁塔,山脚下有一矩形建筑物ABCD.且建筑物周围没有开阔平整地带.该建筑物顶端宽度AD和高度DC都可以直接测得。从A、D、C三点可看到塔顶端H.可供使用的测员工具有皮尺,测倾器(即测角仪).
(1)请你根据现有条件,充分利用矩形建筑物.设计一个测量塔顶端到地面高度HG的方案.具体要求如下:
①测量数据尽可能少;
②在所给图形上,画出你设计的测量的平面图,并将应测数据标记在图形上(如果测A、D间距离,用m表示;如果测D、C间距离,用n表示;如果测角,用α、β、γ等表示.测倾器高度不计)
(2)根据你测量的数据,计算塔顶到地面的高度HG(用字母I表示)
方案一
(1)如图(a)(测四个数据)
AD=m,CD=n,∠HDM= ,∠HAM=β
(2)设HG=x,HM=x-n,
在Rt△HDM中,tan = ,DM=
在Rt△HAM中,tanβ= ,DM=
∵AM-DM=AD,
∴ - =m,
x= +n.
方案二
(1)如图(b)(测三个数据)
CD=n,∠HDM=α,∠HCG=γ.
(2)设HG=x,HM=x-n,
在Rt△CHG中,tanγ= ,CG= ,
在Rt△HDM中,tanα = ,DM= ,
∵CG=DM,
∴ = ,x=
1.如图,有一斜坡AB长40m,坡顶离地面的
高度为20m,求此斜坡的倾斜角.
A
C
B
解:如图∠C=90°,AB=40, BC=20
∴sin∠A=
∴∠A=30°
课堂练习
2. 水库大坝的截面是梯形ABCD,其中AD∥BC,坝顶AD=6m,
坡长CD=8m,坡底BC=30m,∠ADC=135°.
(1)求坡角∠ABC的大小;
(2)如果坝长100m,那么修建这个大坝共需多少土石料
(结果精确到0.01m3).
A
D
B
C
A
D
B
C
F
E
解:(1)如图,作AE⊥BC,DF⊥BC
则∠FDC=135°-90°=45°
∴AE=DF=FC=CDsin45°=
∴BE=BC-FC-EF=BC-FC-AD=24-
∴tan∠ABC=
∴∠ABC≈17°8′21″
A
D
B
C
F
E
解:(2)S梯形ABCD=(6+30)× ÷2= (m2)
V=100×S梯形ABCD=100× ≈10182.34(m3)
建筑大坝共需10182.34m3的土石.
图K-7-3
B
图K-7-4
B
[解析] B 先根据CD=20 m,DE=10 m得出∠DCE=30°,故可得出∠DCB=90°,再由∠BDF=30°可知∠DBF=60°,由DF∥AE可得出∠BGF=∠BCA=60°,故∠GBF=30°,所以∠DBC=30°,再由锐角三角函数的定义即可得出结论.
图K-7-5
A
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
(5)学会使用了测角仪
(6)研讨了测量可到达底部和不可以到达底部的物体高度的方案.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
