2.3确定二次函数的表达式 课件(共31张PPT)
文档属性
| 名称 | 2.3确定二次函数的表达式 课件(共31张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 627.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
北师大版九年级下册数学
第二章 二次函数
2.3确定二次函数的表达式
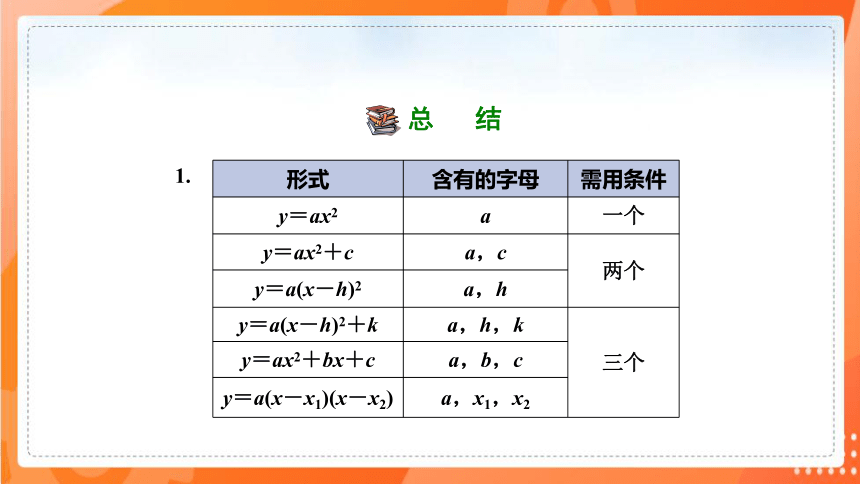
一名学生推铅球时,铅球行进高度y (m )与水平距离
x ( m )之间的关系如图所示,其中(4, 3)为图象的顶点,
你能求出y与x之间的关系式吗?
知识点
确定二次函数的表达式
想一想
确定二次函数的表达式需要几个条件?与同伴进行交流.
1
总 结
形式 含有的字母 需用条件
y=ax2 a 一个
y=ax2+c a,c 两个
y=a(x-h)2 a,h y=a(x-h)2+k a,h,k 三个
y=ax2+bx+c a,b,c y=a(x-x1)(x-x2) a,x1,x2 1.
总 结
2.二次函数的表达式中有几个待定的字母,就需要有
几个条件去求解;反过来,要根据题目中给定的条
件数目去设相应的函数表达式并求解,这种方法叫
待定系数法.
1.用待定系数法求二次函数的表达式:
(1)若给出抛物线上任意三点,通常可设一般式y=ax2
+bx+c(a≠0).
(2)若给出抛物线的顶点坐标或对称轴或最值,通常可
设顶点式y=a(x-h)2+k(a≠0).
(3)若给出抛物线与x轴的交点或与x轴的交点距离,通
常可设交点式y=a(x-x1)(x-x2)(a≠0).
要点精析:(1)求二次函数表达式的几种方法之间是相
互联系的,而不是孤立的,不同的设法是根据不同
的已知条件来确定的.
(2)在选用不同的设法时,应具体问题具体分析,特
别是当已知条件不是上述所列举的几种情形时,
应灵活地选用不同的方法来求解,以达到事半功
倍的效果.
2.易错警示:根据题目中的条件设出相应的函数表
达式.
例1 已知二次函数y=ax +c的图象经过点(2,3)和
(-1,-3),求这个二次函数的表达式.
解:将点(2, 3)和(-1,-3)的坐标分别代入表达式y= ax2+c,
得
解这个方程组,得
所以,所求二次函数表达式为y=2x2-5.
导引:由题意可得A点的坐标为(2,-1).∵抛物线的顶点在
坐标原点,∴可设抛物线对应的函数表达式为y=ax2.
将点A(2,-1)的坐标代入,可得a=- ,∴抛物线
对应的函数表达式为y=- x2.
例2 〈衡阳改编,图文信息题〉如图,已知
抛物线的顶点在坐标原点,矩形ABCD
的顶点A,D在抛物线上,且AD平行于
x轴,交y轴于点F,AB的中点E在x轴
上,B点的坐标为(2,1),此抛物线对应的函数表达式
为___________.
总 结
如果已知函数图象,函数图象的位置可决定函数
的形式,特别关注的是顶点的位置:若顶点在原点上,
则y=ax2(a≠0);若顶点在y轴上,则y=ax2+c(a≠0);
若顶点在x轴上,则y=a(x-h)2(a≠0);若顶点不在坐
标轴上,则y=a(x-h)2+k(a≠0).
1 (1)已知二次函数y=x2+bx+c的图象经过(1,1)与(2, 3)
两点,求这个二次函数的表达式;
(2)请更换第(1)题中的部分已知条件,重新设计一个
求二次函数y=x2+bx+c表达式的题目,使所求得的
二次函数与第(1)题相同.
2
知识点
用一般式(三点式)确定二次函数表达式
例3 已知二次函数的图象经过(-1,10),(1,4),(2, 7)三点,
求这个二次函数的表达式,并写出它的对称轴和
顶点坐标.
解:设所求二次函数的表达式为y=ax2+bx+c.
将三点(-1,10),(1,4),(2, 7)的坐标分别代入表达式,得
所以,所求二次函数表达式为 y=2x2-3x+5 .
因为y=2x2-3x+5=2
所以,二次函数图象的对称轴为直线 ,
顶点坐标为
例4〈武汉改编〉科幻小说《实验室的故事》中,有这样一个情节,
科学家把一种珍奇的植物分别放在不同温度的环境中,经过一
天后,测试出这种植物高度的增长情况(如下表):
由这些数据,科学家推测出植物每天高度增长量y是温度x的函
数,且这种函数是一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说
明不选择另一种函数的理由.
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量
的总和超过250 mm,那么实验室的温度x应该在哪个范围内
选择?请直接写出结果.
温度x/℃ … -4 -2 0 2 4 4.5 …
植物每天高度 增长量y/mm … 41 49 49 41 25 19.75 …
导引:由x,y的对应关系,易知y是x的二次函数.
解:(1)选择二次函数,设y=ax2+bx+c,
∴y关于x的函数关系式是y=-x2-2x+49.
不选另外一个函数的理由:点(-4,41),(-2,49),(2,41)
等不在同一直线上,∴y不是x的一次函数.
(2)由(1)得y=-x2-2x+49,∴y=-(x+1)2+50.
∵a=-1<0,∴当x=-1时,y有最大值50.
即当温度为-1 ℃时,这种植物每天高度的增长量最大.
(3)-6<x<4.
总 结
已知抛物线过三点,求其对应的函数表达式,可采
用一般式;而用一般式求待定系数要经历以下三步:
第一步:设一般式 y=ax2+bx+c;
第二步:将三点的坐标分别代入一般式中,组成一
个三元一次方程组;
第三步:解方程组即可求出a,b,c的值.
1 (2016·临沂)二次函数y=ax2+bx+c,自变量x与函
数y的对应值如表:
下列说法正确的是( )
A.抛物线的开口向下
B.当x>-3时,y随x的增大而增大
C.二次函数的最小值是-2
D.抛物线的对称轴是直线x=-
x … -5 -4 -3 -2 -1 0 …
y … 4 0 -2 -2 0 4 …
2 (中考·宁波)如图,已知二次函数y=ax2+bx+c的图
象过A(2,0),B(0,-1)和C(4,5)三点.
(1)求二次函数的表达式;
(2)设二次函数的图象与x轴的另一
个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+
1,并写出当x在什么范围内时,一次函数的值大于
二次函数的值.
3 已知二次函数的图象经过点(0, 2), (1,0)和(-2,
3),求这个二次函数的表达式.
顶点法求二次函数的表达式
选取顶点(-2,1)和点(1,-8),试求出这个二次函数的表达式.
解:设这个二次函数的表达式是y=a(x-h)2+k,把顶点(-2,1)代入y=a(x-h)2+k得
y=a(x+2)2+1,
再把点(1,-8)代入上式得
a(1+2)2+1=-8,
解得 a=-1.
∴所求的二次函数的表达式是y=-(x+2)2+1或y=-x2-4x-3.
知识点
3
归纳总结
顶点法求二次函数的方法
这种知道抛物线的顶点坐标,求表达式的方法叫做顶点法.其步骤是:
①设函数表达式是y=a(x-h)2+k;
②先代入顶点坐标,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a用数值换掉,写出函数表达式.
针对训练
2. 一个二次函数的图象经点 (0, 1),它的顶点坐标为(8,9),求这个二次函数的表达式.
解: 因为这个二次函数的图象的顶点坐标为(8,9),因此,可以设函数表达式为
y=a(x-8)2+9.
又由于它的图象经过点(0 ,1),可得 1=a(0-8)2+9.
解得
∴所求的二次函数的表达式是
解: ∵(-3,0)(-1,0)是抛物线y=ax2+bx+c与x轴的交点.所以可设这个二次函数的表达式是y=a(x-x1)(x-x2).(其中x1、x2为交点的横坐标.因此得
y=a(x+3)(x+1).
再把点(0,-3)代入上式得
a(0+3)(0+1)=-3,
解得a=-1,
∴所求的二次函数的表达式是
y=-(x+3)(x+1),即y=-x2-4x-3.
选取(-3,0),(-1,0),(0,-3),试求出这个二次函数的表达式.
交点法求二次函数的表达式
x
y
O
1
2
-1
-2
-3
-4
-1
-2
-3
-4
-5
1
2
知识点
4
归纳总结
交点法求二次函数表达式的方法
这种知道抛物线与x轴的交点,求表达式的方法叫做交点法.
其步骤是:
①设函数表达式是y=a(x-x1)(x-x2);
②先把两交点的横坐标x1,x2代入到表达式中,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a用数值换掉,写出函数表达式.
想一想
确定二次函数的这三点应满足什么条件?
任意三点不在同一直线上(其中两点的连线可平行于x轴,但不可以平行于y轴.
用待定系数法求二次函数表达式选择类型的方法:
若已知图象上三个任意点的坐标,则利用一般式y=
ax2+bx+c求;若已知图象的顶点坐标(或对称轴或函
数的最值),则利用顶点式y=a(x-h)2+k求;若已知
图象与x轴的两个交点,则利用交点式y=a(x-x1)(x-
x2)求.
1.(衢州·中考)下列四个函数图象中,当x>0时,
y随x的增大而增大的是( )
C
2.(莆田·中考)某同学用描点法画y=ax2+bx+c(a≠0)的图象时,列出如下表格:
经检查,发现只有一处数据计算错误,请你写出这个二次函数的解析式 .
x 0 1 2 3 4
y 3 0 2 0 3
y=x2 4x+3
3.(潼南·中考)如图,在平面直角坐标系中,四边形OABC是菱形,
点C的坐标为(4,0),∠AOC= 60°,垂直于x轴的直线l从y轴出发,
沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC
的两边分别交于点M,N(点M在点N的上方),若△OMN
的面积为S,直线l的运动时间为t 秒(0≤t≤4),则
能大致反映S与t的函数关系的图象是( )
解析:选C.过点A作x轴的垂线,垂足为E,则OE=2,AE= ,当点M在OA
上时,ON=t,MN= ,所以S= (0≤t≤2);当点M在AB上时,MN的
值不变为 ,所以S= (2≤t≤4),故选C.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版九年级下册数学
第二章 二次函数
2.3确定二次函数的表达式
一名学生推铅球时,铅球行进高度y (m )与水平距离
x ( m )之间的关系如图所示,其中(4, 3)为图象的顶点,
你能求出y与x之间的关系式吗?
知识点
确定二次函数的表达式
想一想
确定二次函数的表达式需要几个条件?与同伴进行交流.
1
总 结
形式 含有的字母 需用条件
y=ax2 a 一个
y=ax2+c a,c 两个
y=a(x-h)2 a,h y=a(x-h)2+k a,h,k 三个
y=ax2+bx+c a,b,c y=a(x-x1)(x-x2) a,x1,x2 1.
总 结
2.二次函数的表达式中有几个待定的字母,就需要有
几个条件去求解;反过来,要根据题目中给定的条
件数目去设相应的函数表达式并求解,这种方法叫
待定系数法.
1.用待定系数法求二次函数的表达式:
(1)若给出抛物线上任意三点,通常可设一般式y=ax2
+bx+c(a≠0).
(2)若给出抛物线的顶点坐标或对称轴或最值,通常可
设顶点式y=a(x-h)2+k(a≠0).
(3)若给出抛物线与x轴的交点或与x轴的交点距离,通
常可设交点式y=a(x-x1)(x-x2)(a≠0).
要点精析:(1)求二次函数表达式的几种方法之间是相
互联系的,而不是孤立的,不同的设法是根据不同
的已知条件来确定的.
(2)在选用不同的设法时,应具体问题具体分析,特
别是当已知条件不是上述所列举的几种情形时,
应灵活地选用不同的方法来求解,以达到事半功
倍的效果.
2.易错警示:根据题目中的条件设出相应的函数表
达式.
例1 已知二次函数y=ax +c的图象经过点(2,3)和
(-1,-3),求这个二次函数的表达式.
解:将点(2, 3)和(-1,-3)的坐标分别代入表达式y= ax2+c,
得
解这个方程组,得
所以,所求二次函数表达式为y=2x2-5.
导引:由题意可得A点的坐标为(2,-1).∵抛物线的顶点在
坐标原点,∴可设抛物线对应的函数表达式为y=ax2.
将点A(2,-1)的坐标代入,可得a=- ,∴抛物线
对应的函数表达式为y=- x2.
例2 〈衡阳改编,图文信息题〉如图,已知
抛物线的顶点在坐标原点,矩形ABCD
的顶点A,D在抛物线上,且AD平行于
x轴,交y轴于点F,AB的中点E在x轴
上,B点的坐标为(2,1),此抛物线对应的函数表达式
为___________.
总 结
如果已知函数图象,函数图象的位置可决定函数
的形式,特别关注的是顶点的位置:若顶点在原点上,
则y=ax2(a≠0);若顶点在y轴上,则y=ax2+c(a≠0);
若顶点在x轴上,则y=a(x-h)2(a≠0);若顶点不在坐
标轴上,则y=a(x-h)2+k(a≠0).
1 (1)已知二次函数y=x2+bx+c的图象经过(1,1)与(2, 3)
两点,求这个二次函数的表达式;
(2)请更换第(1)题中的部分已知条件,重新设计一个
求二次函数y=x2+bx+c表达式的题目,使所求得的
二次函数与第(1)题相同.
2
知识点
用一般式(三点式)确定二次函数表达式
例3 已知二次函数的图象经过(-1,10),(1,4),(2, 7)三点,
求这个二次函数的表达式,并写出它的对称轴和
顶点坐标.
解:设所求二次函数的表达式为y=ax2+bx+c.
将三点(-1,10),(1,4),(2, 7)的坐标分别代入表达式,得
所以,所求二次函数表达式为 y=2x2-3x+5 .
因为y=2x2-3x+5=2
所以,二次函数图象的对称轴为直线 ,
顶点坐标为
例4〈武汉改编〉科幻小说《实验室的故事》中,有这样一个情节,
科学家把一种珍奇的植物分别放在不同温度的环境中,经过一
天后,测试出这种植物高度的增长情况(如下表):
由这些数据,科学家推测出植物每天高度增长量y是温度x的函
数,且这种函数是一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说
明不选择另一种函数的理由.
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量
的总和超过250 mm,那么实验室的温度x应该在哪个范围内
选择?请直接写出结果.
温度x/℃ … -4 -2 0 2 4 4.5 …
植物每天高度 增长量y/mm … 41 49 49 41 25 19.75 …
导引:由x,y的对应关系,易知y是x的二次函数.
解:(1)选择二次函数,设y=ax2+bx+c,
∴y关于x的函数关系式是y=-x2-2x+49.
不选另外一个函数的理由:点(-4,41),(-2,49),(2,41)
等不在同一直线上,∴y不是x的一次函数.
(2)由(1)得y=-x2-2x+49,∴y=-(x+1)2+50.
∵a=-1<0,∴当x=-1时,y有最大值50.
即当温度为-1 ℃时,这种植物每天高度的增长量最大.
(3)-6<x<4.
总 结
已知抛物线过三点,求其对应的函数表达式,可采
用一般式;而用一般式求待定系数要经历以下三步:
第一步:设一般式 y=ax2+bx+c;
第二步:将三点的坐标分别代入一般式中,组成一
个三元一次方程组;
第三步:解方程组即可求出a,b,c的值.
1 (2016·临沂)二次函数y=ax2+bx+c,自变量x与函
数y的对应值如表:
下列说法正确的是( )
A.抛物线的开口向下
B.当x>-3时,y随x的增大而增大
C.二次函数的最小值是-2
D.抛物线的对称轴是直线x=-
x … -5 -4 -3 -2 -1 0 …
y … 4 0 -2 -2 0 4 …
2 (中考·宁波)如图,已知二次函数y=ax2+bx+c的图
象过A(2,0),B(0,-1)和C(4,5)三点.
(1)求二次函数的表达式;
(2)设二次函数的图象与x轴的另一
个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+
1,并写出当x在什么范围内时,一次函数的值大于
二次函数的值.
3 已知二次函数的图象经过点(0, 2), (1,0)和(-2,
3),求这个二次函数的表达式.
顶点法求二次函数的表达式
选取顶点(-2,1)和点(1,-8),试求出这个二次函数的表达式.
解:设这个二次函数的表达式是y=a(x-h)2+k,把顶点(-2,1)代入y=a(x-h)2+k得
y=a(x+2)2+1,
再把点(1,-8)代入上式得
a(1+2)2+1=-8,
解得 a=-1.
∴所求的二次函数的表达式是y=-(x+2)2+1或y=-x2-4x-3.
知识点
3
归纳总结
顶点法求二次函数的方法
这种知道抛物线的顶点坐标,求表达式的方法叫做顶点法.其步骤是:
①设函数表达式是y=a(x-h)2+k;
②先代入顶点坐标,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a用数值换掉,写出函数表达式.
针对训练
2. 一个二次函数的图象经点 (0, 1),它的顶点坐标为(8,9),求这个二次函数的表达式.
解: 因为这个二次函数的图象的顶点坐标为(8,9),因此,可以设函数表达式为
y=a(x-8)2+9.
又由于它的图象经过点(0 ,1),可得 1=a(0-8)2+9.
解得
∴所求的二次函数的表达式是
解: ∵(-3,0)(-1,0)是抛物线y=ax2+bx+c与x轴的交点.所以可设这个二次函数的表达式是y=a(x-x1)(x-x2).(其中x1、x2为交点的横坐标.因此得
y=a(x+3)(x+1).
再把点(0,-3)代入上式得
a(0+3)(0+1)=-3,
解得a=-1,
∴所求的二次函数的表达式是
y=-(x+3)(x+1),即y=-x2-4x-3.
选取(-3,0),(-1,0),(0,-3),试求出这个二次函数的表达式.
交点法求二次函数的表达式
x
y
O
1
2
-1
-2
-3
-4
-1
-2
-3
-4
-5
1
2
知识点
4
归纳总结
交点法求二次函数表达式的方法
这种知道抛物线与x轴的交点,求表达式的方法叫做交点法.
其步骤是:
①设函数表达式是y=a(x-x1)(x-x2);
②先把两交点的横坐标x1,x2代入到表达式中,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a用数值换掉,写出函数表达式.
想一想
确定二次函数的这三点应满足什么条件?
任意三点不在同一直线上(其中两点的连线可平行于x轴,但不可以平行于y轴.
用待定系数法求二次函数表达式选择类型的方法:
若已知图象上三个任意点的坐标,则利用一般式y=
ax2+bx+c求;若已知图象的顶点坐标(或对称轴或函
数的最值),则利用顶点式y=a(x-h)2+k求;若已知
图象与x轴的两个交点,则利用交点式y=a(x-x1)(x-
x2)求.
1.(衢州·中考)下列四个函数图象中,当x>0时,
y随x的增大而增大的是( )
C
2.(莆田·中考)某同学用描点法画y=ax2+bx+c(a≠0)的图象时,列出如下表格:
经检查,发现只有一处数据计算错误,请你写出这个二次函数的解析式 .
x 0 1 2 3 4
y 3 0 2 0 3
y=x2 4x+3
3.(潼南·中考)如图,在平面直角坐标系中,四边形OABC是菱形,
点C的坐标为(4,0),∠AOC= 60°,垂直于x轴的直线l从y轴出发,
沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC
的两边分别交于点M,N(点M在点N的上方),若△OMN
的面积为S,直线l的运动时间为t 秒(0≤t≤4),则
能大致反映S与t的函数关系的图象是( )
解析:选C.过点A作x轴的垂线,垂足为E,则OE=2,AE= ,当点M在OA
上时,ON=t,MN= ,所以S= (0≤t≤2);当点M在AB上时,MN的
值不变为 ,所以S= (2≤t≤4),故选C.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
