5.2勾股定理

课件22张PPT。 在数学的天地里，重要的不是我们知道什么，而是我们应该怎样知道。
——毕达哥拉斯青岛版义务教育课程
标准实验教科书
八年级数学上册5.2 勾 股 定 理
国际数学家大会是全球最高水平的数学科学学术会议，被誉为数学界的“奥林匹克运动会”。2002年8月20日，在北京召开了第24届国际数学家大会，大会的会标取材于我国古代数学家赵爽的“勾股圆方图”，它标志着中国古代的数学成就。学习目标：
1、经历勾股定理的探索过程，感受数形结合的数学思想。
2、掌握勾股定理，并会运用勾股定理解决一些与直角三角形有关的简单问题。
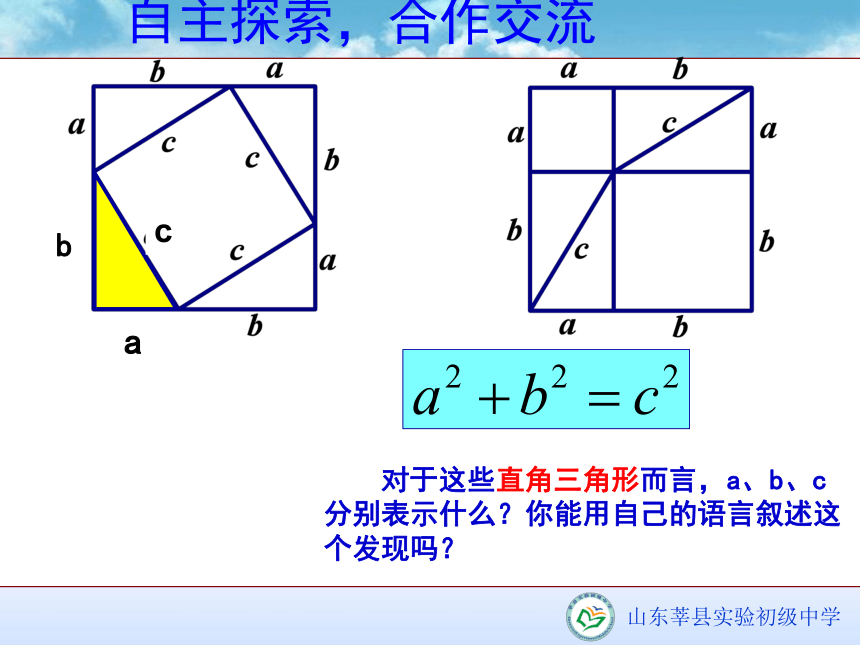
3、尝试用多种方法验证勾股定理，体验解决问题方法的多样性。情境导入，明确目标1、图中两个大正方形的面积相等吗？
2、两幅图中彩色部分的四个直角三角形总面积相等吗？
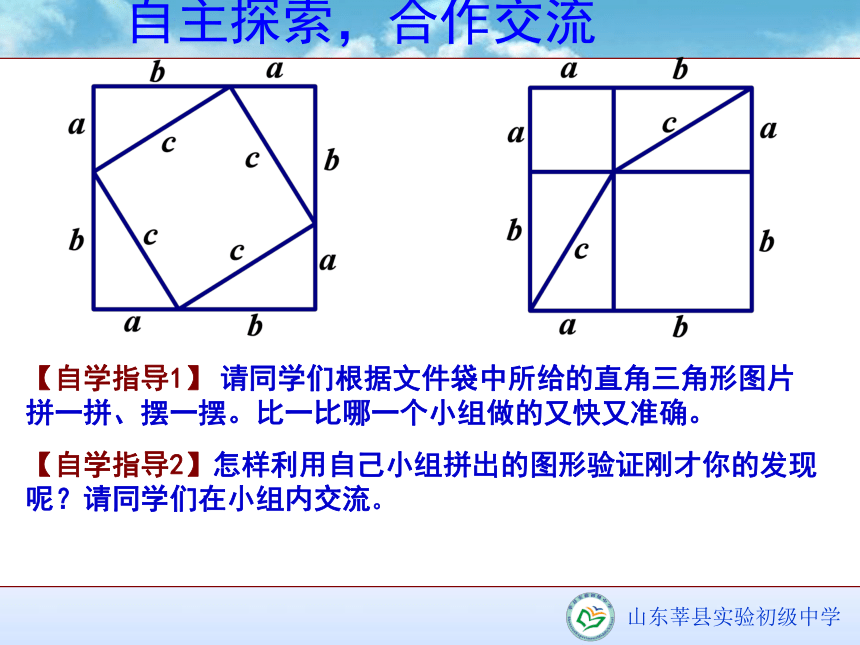
3、两幅图中空白部分的面积有什么关系？你能用式子表达自己的发现吗？自主探索，合作交流 用8个同样大小的直角三角形摆放在如图所示的2个正方形内，请同学们观察两个图形，思考下列问题：自主探索，合作交流 对于这些直角三角形而言，a、b、c分别表示什么？你能用自己的语言叙述这个发现吗？自主探索，合作交流【自学指导1】 请同学们根据文件袋中所给的直角三角形图片拼一拼、摆一摆。比一比哪一个小组做的又快又准确。
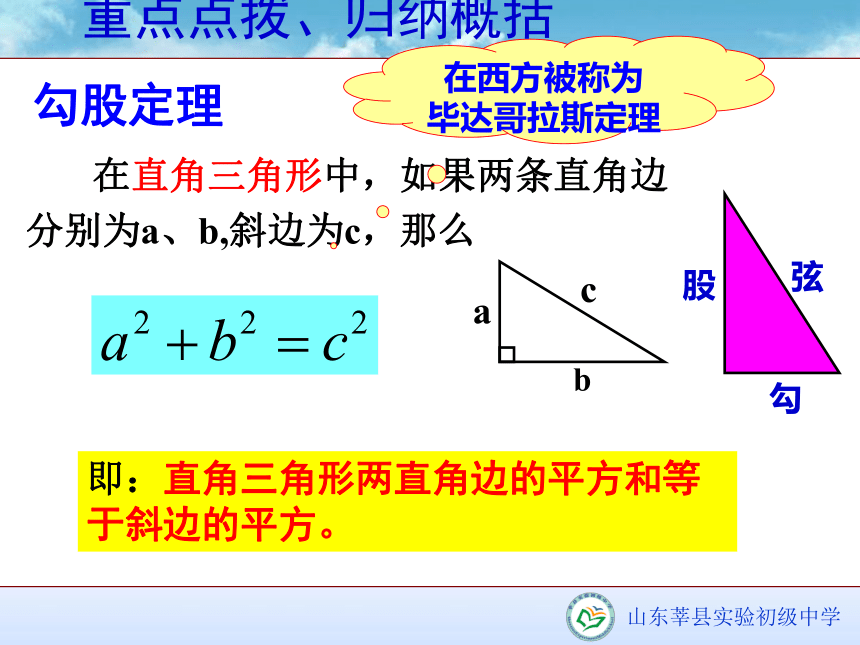
【自学指导2】怎样利用自己小组拼出的图形验证刚才你的发现呢？请同学们在小组内交流。勾股定理 在直角三角形中，如果两条直角边
分别为a、b,斜边为c，那么即：直角三角形两直角边的平方和等于斜边的平方。在西方被称为
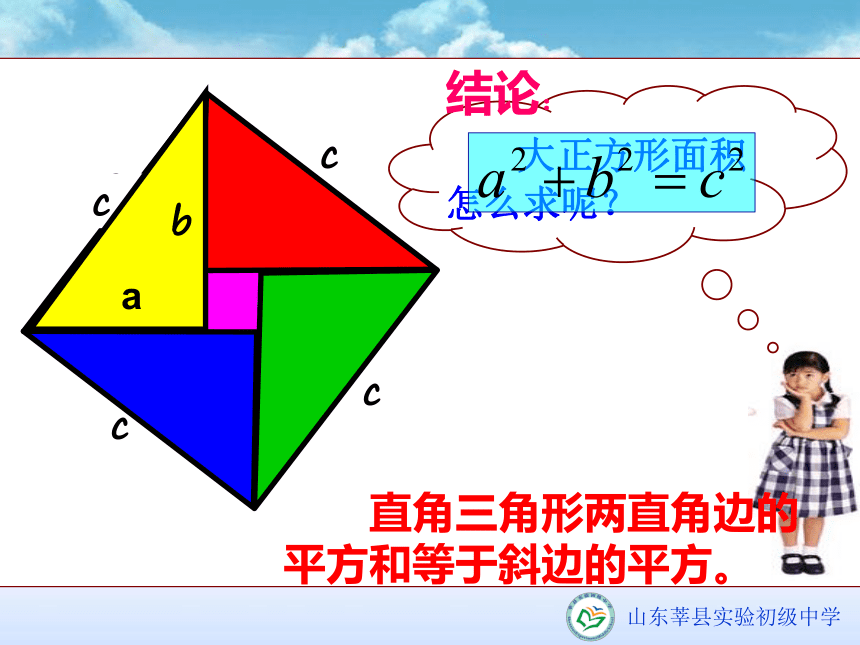
毕达哥拉斯定理 重点点拨、归纳概括结论： 直角三角形两直角边的平方和等于斜边的平方。学以致用，巩固新知 如图，从电线杆OA的顶端A点，扯一根钢丝绳固定在地面上的B点，这根钢丝绳的长度是多少？例1【自学指导】请同学们认真自学课本129页的例1，了解应用勾股定理解决问题的一般步骤，2分钟后，回答有关问题。1、题目中已知的是直角三角形哪两条边的长？
2、怎样运用勾股定理求Rt△AOB的斜边AB的长度？学以致用，巩固新知 如图，从电线杆OA的顶端A点，扯一根钢丝绳固定在地面上的B点，这根钢丝绳的长度是多少？解：在Rt△AOB中，
AB2=OA2+OB2∵OA=8,OB=6
∴即：钢丝绳的长度为10米。例学以致用，巩固新知解：在Rt△AOB中，
∵AB2=OA2+OB2
即：∵AB=10,OB=6
∴变式： 如图，从电线杆OA的顶端A点，扯一根钢丝绳固定在地面上的B点，这根电线杆的高度是多少？学以致用，巩固新知1、勾股定理揭示了哪一类三角形中的什么元素之间的关系？
2、如果已知直角三角形中的任意两条边，怎样运用勾股定理求第三边的长？ 直角三角形两直角边的平方和等于斜边的平方。你能快速求出下列直角三角形中未知边的长度吗？学以致用，巩固新知X= .X= .45体会.分享1、这节课你学会了哪些知识？用到了哪些数学思想？
2、运用勾股定理解决问题时应该注意哪些方面？
3、你有什么体会与感想？畅所欲言回顾反思，提炼精华勾股定理内 容直角三角形两直角边的平方和等于斜边的平方已知直角三角形的两边会求第三边的长度会利用勾股定理解决一些简单的问题 回顾反思，提炼精华学习目标：
1、经历勾股定理的探索过程，感受数形结合的数学思想。
2、掌握勾股定理，并会运用勾股定理解决一些与直角三角形有关的简单问题。
3、尝试用多种方法验证勾股定理，体验解决问题方法的多样性。
数形结合思想1、在Rt △ABC中，a、b、c分别是∠ A、∠ B、∠ C的对边，∠C=90°.
①若a = 3，b = 4，则c = 　　　；
②若c=13，b = 12，则a = .
2.求下列直角三角形中未知边的长:
3、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间
加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米4.某楼发生火灾，消防车立即赶到距大楼6米的地方搭建云梯，
升起云梯到达火灾窗口。已知云梯长10米，问发生火灾的窗口
距离地面多高？（不计消防车的高度）
解：由题意得：BC=6，AB=10
在Rt△ABC中，根据勾股定理可得：AC2+BC2=AB2
即：AC2+62=102 解得：AC=8
所以，发生火灾的窗口距离地面8米。
达标检测，当堂反馈55X=13X=15C祝同学们学习进步！例 如图，某建筑工地需要制作等腰三角形支架，为了增加支架的耐压性，需要加一根中柱AD（D为BC的中点）如果AB=AC=5米，BC=8米，求AD的长。解：∵D为BC的中点，BC=8
∴BD=CD=4
∵AB=AC,D为BC的中点
∴ AD⊥BC
即：∠ADB=∠ADC=90°
在Rt△ADB中
活学活用，巩固新知勾股史话 我国是最早了解勾股定理的国家之一，在《周髀算经》中记录商高的一段话。商高说：“…故折矩，勾广三，股修四，经隅五。” 意思就是说：当直角三角形的两条直角边分别为3（短边）和4（长边）时，径隅（就是弦）则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。故称之为“勾股定理”或“商高定理” 在西方，古希腊数学家毕达哥达斯学派最早证明了勾股定理，所以国外人们就把这个定理称为“毕达哥拉斯定理”，相传，毕达哥拉斯学派找到了勾股定理的证明后，欣喜若狂，杀了一百头牛祭神，由此，又有“百牛定理”之称。为纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票。
勾股史话毕达哥拉斯（公元前572-前497年）古希腊著名的哲学家、数学家、天文学家.