2.4二次函数的应用 课件(共36张PPT)
文档属性
| 名称 | 2.4二次函数的应用 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 572.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 10:42:26 | ||
图片预览











文档简介
(共36张PPT)
北师大版九年级下册数学
第二章 二次函数
2.4二次函数的应用
【例 1】某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长 69 米 的不锈钢栅栏围成,与墙平行的一边留一个宽为 3 米 的出入口,如图,如何设计才能使园地的面积最大?下面是两位学生争议的情境:
知识点 1 求几何图形的最大面积问题
分析:(1)设 AB=x 米,根据等式x+x+BC=69+3,可以求出 BC 的表达式.
(2)得出面积关系式,根据所求关系式进行判断即可.
解:(1)设 AB=x 米,
则 BC=69+3-2x=72-2x.
(2)小英的说法正确.
矩形面积 S=x(72-2x)=-2(x-18)2+648.
∵72-2x>0,∴x<36,∴0∴当 x=18 时,S 取最大值,此时 x≠72-2x,
∴面积最大的不是正方形.
1. 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为 80 m 的围网在水库中围成了如图的①②③三块矩形区域,而且这三块矩形区域的面积相等. 设 BC 的长度为 x m,矩形区域 ABCD 的面积为 y m2.
(1)求 y 与 x 之间的函数关系式,并注明自变量 x 的取值范围.
(2)当 x 为何值时,y 有最大值?
最大值是多少?
分析:(1)根据三个矩形的面积相等,得到矩形 AEFD 的面积是矩形 BCFE 的面积的 2 倍,可得出 AE=2BE. 设 BE=a,则 AE=2a,表示出 a与 2a,进而表示出 y 与 x 的关系式,并求出 x 的范围即可.
(2)利用二次函数的性质求出 y 的最大值,以及此时 x 的值即可.
【例 2】一个足球被从地面向上踢出,它距地面的高度 h(m)与足球被踢出后经过的时间 t(s)之间具有函数关系 h=at 2+19.6t. 已知足球被踢出后经过 4 s 落地,则足球距地面的最大高度是 m.
知识点 2:二次函数在生活中的应用
19.6
分析:首先由题意,得 当 t=4 时,h=0,然后代入函数关系 h=at 2+19.6t 可得 a 的值,最后利用函数解析式计算出 h 的最大值即可.
解析:由题意,得 当 t=4 时,h=0,
因此 0=16a+19.6×4,
解得 a=-4.9,
∴函数关系为 h=-4.9t 2+19.6t ,
∴足球距地面的最大高度是
=19.6(m).
2. 一位运动员投掷铅球,如果铅球运行时离地面的高度为 y(米)关于水平距离 x(米)的函数解析式为 y=- x2+ x+ ,那么铅球运动过程中最高点离地面的距离为 米.
3
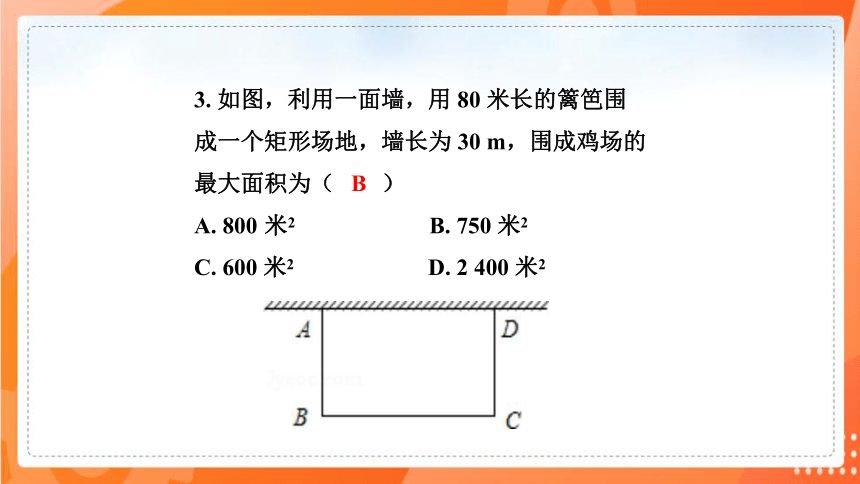
3. 如图,利用一面墙,用 80 米长的篱笆围成一个矩形场地,墙长为 30 m,围成鸡场的最大面积为( )
A. 800 米2 B. 750 米2
C. 600 米2 D. 2 400 米2
B
4. 某幢建筑物从 16 m 高的窗口 A,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图),如果抛物线的最高点 M 离墙 1 m,离地面 18 m,则水流落地点 B 离墙的距离 OB 是 ( )
A. 2 m B. 3 m C. 4 m D. 5 m
C
5. 如图是一个横断面为抛物线形状的拱桥,当水面宽 4 米时,拱顶(拱桥洞的最高点)离水面 2 米,水面下降 1 米时,水面的宽度为 米.
6. 有长 24 m 的篱笆,一面利用长为 12 m 的围墙围成如图中间隔有一道篱笆的矩形花圃. 设花圃垂直于墙的一边长为 x m,面积为 S m2. 则 S 与 x 的函数关系式是 ,x 的取值范围为 .
4≤x<8
S =(24-3x)x
7. 如图,某涵洞的截面是抛物线形,现测得水面宽 AB=1.6 m,涵洞顶点 O 到水面的距离
CO 为 2.4 m,在图中的直角坐标系内,涵洞
截面所在抛物线的解析式是 .
y =- x2
8. 某居民小区要在一块一边靠墙(墙长 15 米)的空地上修建一个矩形花园 ABCD,花园的一边靠墙,另三边用总长 40 米的栅栏围成(如图). 若设花园的 BC 边长为 x 米,花园的面积为 y 米2.
(1)求 y 与 x 之间的函数关系式,并写出自变量 x 的取值范围.
(2)满足条件的花园面积能否达到 150 米2?若能,请求出 x 的值;若不能,请说明理由.
(3)当 x 是多少时,矩形场地面积 y 最大?最大面积是多少?
解:(1)由题意可知,BC 为 x 米,
则 AB= =20 - .
∵矩形 ABCD 的面积为 AB BC,
∴y =(20- )x=20x- x2=- x2+20x,
自变量 x 的取值范围为 0(2)能达到.
由题意知,当 y=150 时,- x2+20x=150,
解得 x1=10,x2=30(不符合题意,舍去),
故 当 x=10 时,花园面积能达到 150 米2.
(3)∵a=- <0,
当 0∴当 x=15 时,y 取最大值,最大值是
- ×152+20×15=187.5.
答:当 x 是 15 米时,矩形场地面积 y 最大,最大面积是 187.5 米2.
9. 一块草坪的护栏是由 50 段形状相同的抛物线组成,如图,为了牢固期间,每段护栏需按间距0.4 m 加设不锈钢管做成的立柱. 为了计算所需不锈钢管立柱的总长度,设计人员测得如图的数据,则需要不锈钢管的总长度为 米.
80
10. 竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔 1 秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后 1.1 秒时到达相同的最大离地高度,第一个小球抛出后 t 秒时在空中与第二个小球的离地高度相同,则 t= .
1.6
1. 求销售中的最大利润问题一般是运用“总利润=总售价 - ”或“总利润= ×销售数量” 建立利润与价格之间的函数关系式.
2. 求实际问题中的最值问题时,一般分为三步:
(1)利用应用题中的已知条件和学过的有关数学公式列出关系式.
(2)把关系式转化为 的关系式.
(3)求二次函数的最大值或最小值.
每件商品的利润
总成本
二次函数
知识点 3 销售中的最大利润问题
3. 一个直角三角形的两条直角边长的和为 20 cm,其中一直角边长为 x cm,面积为 y cm2,则 y 与x 的函数的关系式是( )
A. y=20x÷2 B. y=x(20 -x)
C. y=x(20 -x)÷2 D. y=x(10 -x)
知识小测
C
4. 已知某商店铺第 17 届仁川亚运会吉祥物毛绒玩具每件的进价为 30 元,在某段时间内若以每件 x 元(30≤x≤50,且 x 为整数)出售,可卖出(50-x)件,若要使该店铺销售该玩具的利润最大,每件的售价为( )
A. 35 元 B. 40 元 C. 45 元 D. 48 元
B
【例 1】大学生小张摆摊销售一批小家电,进价 40 元,经市场考察知,当销售进价为 52 元时,可售出 180 个,且定价 x(元)与销售减少量 y(个)满足关系式:y=10(x -52),问:
(1)若他打算获利 2 000 元,且投资尽量少,则应进货多少个?定价是多少?
(2)若他想获得最大利润,则定价及进货分别是多少?
分析:(1)利用每个小家电的利润×销售的个数=总利润,列方程解答即可.
(2)设利润为 w,利用(1)的数量关系列出函数,运用配方法解决问题.
解:(1)设定价为 x 元,
则进货 180-10(x-52)=180-10x+520=700-10x,
所以(x-40)(700-10x)=2 000,
解得 x1=50,x2=60.
因为投资尽量少,所以应进货 100 个,定价 60 元.
答:商店若准备获利 2 000 元,定价为 60 元,应进货 100 个.
(2)设利润为 w 元,
则 w=(x-40)(700-10x)=-10x2+1 100x-28 000 =-10(x-55)2 +2 250,
因此当 x=55 时,w最大=2 250.
答:当定价为 55 元时,获得的利润最大,最大利润是 2 250 元.
【例 2】某超市对进货价为 10 元/千克的某种苹果的销售情况进行统计,发现每天销售量 y(千克)与销售价 x(元/千克)存在一次函数关系,如图.
知识点 4 二次函数与一次函数的综合运用
(1)求 y 关于 x 的函数关系式(不要求写出 x 的取值范围).
(2)应怎样确定销售价,使该品种苹果每天的销售利润最大?最大利润是多少?
分析:(1)由图象过点(20,20)和(30,0),利用待定系数法求直线的解析式.
(2)每天的利润=每千克的利润×销售量. 据此列出表达式,运用函数性质解答.
解:(1)设 y=kx+b.
由图象可知,
解得
∴y=-2x+60.
(2)p=(x-10)y =(x-10)(-2x+60)
=-2x2+80x-600.
∵a=-2<0,∴p 有最大值,
当 x=- =20 时,p最大 =200.
即当销售单价为 20元/千克时,每天可获得最大利润 200元.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版九年级下册数学
第二章 二次函数
2.4二次函数的应用
【例 1】某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长 69 米 的不锈钢栅栏围成,与墙平行的一边留一个宽为 3 米 的出入口,如图,如何设计才能使园地的面积最大?下面是两位学生争议的情境:
知识点 1 求几何图形的最大面积问题
分析:(1)设 AB=x 米,根据等式x+x+BC=69+3,可以求出 BC 的表达式.
(2)得出面积关系式,根据所求关系式进行判断即可.
解:(1)设 AB=x 米,
则 BC=69+3-2x=72-2x.
(2)小英的说法正确.
矩形面积 S=x(72-2x)=-2(x-18)2+648.
∵72-2x>0,∴x<36,∴0
∴面积最大的不是正方形.
1. 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为 80 m 的围网在水库中围成了如图的①②③三块矩形区域,而且这三块矩形区域的面积相等. 设 BC 的长度为 x m,矩形区域 ABCD 的面积为 y m2.
(1)求 y 与 x 之间的函数关系式,并注明自变量 x 的取值范围.
(2)当 x 为何值时,y 有最大值?
最大值是多少?
分析:(1)根据三个矩形的面积相等,得到矩形 AEFD 的面积是矩形 BCFE 的面积的 2 倍,可得出 AE=2BE. 设 BE=a,则 AE=2a,表示出 a与 2a,进而表示出 y 与 x 的关系式,并求出 x 的范围即可.
(2)利用二次函数的性质求出 y 的最大值,以及此时 x 的值即可.
【例 2】一个足球被从地面向上踢出,它距地面的高度 h(m)与足球被踢出后经过的时间 t(s)之间具有函数关系 h=at 2+19.6t. 已知足球被踢出后经过 4 s 落地,则足球距地面的最大高度是 m.
知识点 2:二次函数在生活中的应用
19.6
分析:首先由题意,得 当 t=4 时,h=0,然后代入函数关系 h=at 2+19.6t 可得 a 的值,最后利用函数解析式计算出 h 的最大值即可.
解析:由题意,得 当 t=4 时,h=0,
因此 0=16a+19.6×4,
解得 a=-4.9,
∴函数关系为 h=-4.9t 2+19.6t ,
∴足球距地面的最大高度是
=19.6(m).
2. 一位运动员投掷铅球,如果铅球运行时离地面的高度为 y(米)关于水平距离 x(米)的函数解析式为 y=- x2+ x+ ,那么铅球运动过程中最高点离地面的距离为 米.
3
3. 如图,利用一面墙,用 80 米长的篱笆围成一个矩形场地,墙长为 30 m,围成鸡场的最大面积为( )
A. 800 米2 B. 750 米2
C. 600 米2 D. 2 400 米2
B
4. 某幢建筑物从 16 m 高的窗口 A,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图),如果抛物线的最高点 M 离墙 1 m,离地面 18 m,则水流落地点 B 离墙的距离 OB 是 ( )
A. 2 m B. 3 m C. 4 m D. 5 m
C
5. 如图是一个横断面为抛物线形状的拱桥,当水面宽 4 米时,拱顶(拱桥洞的最高点)离水面 2 米,水面下降 1 米时,水面的宽度为 米.
6. 有长 24 m 的篱笆,一面利用长为 12 m 的围墙围成如图中间隔有一道篱笆的矩形花圃. 设花圃垂直于墙的一边长为 x m,面积为 S m2. 则 S 与 x 的函数关系式是 ,x 的取值范围为 .
4≤x<8
S =(24-3x)x
7. 如图,某涵洞的截面是抛物线形,现测得水面宽 AB=1.6 m,涵洞顶点 O 到水面的距离
CO 为 2.4 m,在图中的直角坐标系内,涵洞
截面所在抛物线的解析式是 .
y =- x2
8. 某居民小区要在一块一边靠墙(墙长 15 米)的空地上修建一个矩形花园 ABCD,花园的一边靠墙,另三边用总长 40 米的栅栏围成(如图). 若设花园的 BC 边长为 x 米,花园的面积为 y 米2.
(1)求 y 与 x 之间的函数关系式,并写出自变量 x 的取值范围.
(2)满足条件的花园面积能否达到 150 米2?若能,请求出 x 的值;若不能,请说明理由.
(3)当 x 是多少时,矩形场地面积 y 最大?最大面积是多少?
解:(1)由题意可知,BC 为 x 米,
则 AB= =20 - .
∵矩形 ABCD 的面积为 AB BC,
∴y =(20- )x=20x- x2=- x2+20x,
自变量 x 的取值范围为 0
由题意知,当 y=150 时,- x2+20x=150,
解得 x1=10,x2=30(不符合题意,舍去),
故 当 x=10 时,花园面积能达到 150 米2.
(3)∵a=- <0,
当 0
- ×152+20×15=187.5.
答:当 x 是 15 米时,矩形场地面积 y 最大,最大面积是 187.5 米2.
9. 一块草坪的护栏是由 50 段形状相同的抛物线组成,如图,为了牢固期间,每段护栏需按间距0.4 m 加设不锈钢管做成的立柱. 为了计算所需不锈钢管立柱的总长度,设计人员测得如图的数据,则需要不锈钢管的总长度为 米.
80
10. 竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔 1 秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后 1.1 秒时到达相同的最大离地高度,第一个小球抛出后 t 秒时在空中与第二个小球的离地高度相同,则 t= .
1.6
1. 求销售中的最大利润问题一般是运用“总利润=总售价 - ”或“总利润= ×销售数量” 建立利润与价格之间的函数关系式.
2. 求实际问题中的最值问题时,一般分为三步:
(1)利用应用题中的已知条件和学过的有关数学公式列出关系式.
(2)把关系式转化为 的关系式.
(3)求二次函数的最大值或最小值.
每件商品的利润
总成本
二次函数
知识点 3 销售中的最大利润问题
3. 一个直角三角形的两条直角边长的和为 20 cm,其中一直角边长为 x cm,面积为 y cm2,则 y 与x 的函数的关系式是( )
A. y=20x÷2 B. y=x(20 -x)
C. y=x(20 -x)÷2 D. y=x(10 -x)
知识小测
C
4. 已知某商店铺第 17 届仁川亚运会吉祥物毛绒玩具每件的进价为 30 元,在某段时间内若以每件 x 元(30≤x≤50,且 x 为整数)出售,可卖出(50-x)件,若要使该店铺销售该玩具的利润最大,每件的售价为( )
A. 35 元 B. 40 元 C. 45 元 D. 48 元
B
【例 1】大学生小张摆摊销售一批小家电,进价 40 元,经市场考察知,当销售进价为 52 元时,可售出 180 个,且定价 x(元)与销售减少量 y(个)满足关系式:y=10(x -52),问:
(1)若他打算获利 2 000 元,且投资尽量少,则应进货多少个?定价是多少?
(2)若他想获得最大利润,则定价及进货分别是多少?
分析:(1)利用每个小家电的利润×销售的个数=总利润,列方程解答即可.
(2)设利润为 w,利用(1)的数量关系列出函数,运用配方法解决问题.
解:(1)设定价为 x 元,
则进货 180-10(x-52)=180-10x+520=700-10x,
所以(x-40)(700-10x)=2 000,
解得 x1=50,x2=60.
因为投资尽量少,所以应进货 100 个,定价 60 元.
答:商店若准备获利 2 000 元,定价为 60 元,应进货 100 个.
(2)设利润为 w 元,
则 w=(x-40)(700-10x)=-10x2+1 100x-28 000 =-10(x-55)2 +2 250,
因此当 x=55 时,w最大=2 250.
答:当定价为 55 元时,获得的利润最大,最大利润是 2 250 元.
【例 2】某超市对进货价为 10 元/千克的某种苹果的销售情况进行统计,发现每天销售量 y(千克)与销售价 x(元/千克)存在一次函数关系,如图.
知识点 4 二次函数与一次函数的综合运用
(1)求 y 关于 x 的函数关系式(不要求写出 x 的取值范围).
(2)应怎样确定销售价,使该品种苹果每天的销售利润最大?最大利润是多少?
分析:(1)由图象过点(20,20)和(30,0),利用待定系数法求直线的解析式.
(2)每天的利润=每千克的利润×销售量. 据此列出表达式,运用函数性质解答.
解:(1)设 y=kx+b.
由图象可知,
解得
∴y=-2x+60.
(2)p=(x-10)y =(x-10)(-2x+60)
=-2x2+80x-600.
∵a=-2<0,∴p 有最大值,
当 x=- =20 时,p最大 =200.
即当销售单价为 20元/千克时,每天可获得最大利润 200元.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
