2.5二次函数与一元二次方程 课件(共30张PPT)
文档属性
| 名称 | 2.5二次函数与一元二次方程 课件(共30张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 678.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 10:44:54 | ||
图片预览










文档简介
(共30张PPT)
北师大版九年级下册数学
第二章 二次函数
2.5二次函数与一元二次方程
创设情境,导入新课
(1)一次函数y=x+2的图象与x轴的交点为( , )
一元一次方程x+2=0的根为_______.
(2) 一次函数y=-3x+6的图象与x轴的交点为( , )
一元一次方程-3x+6=0的根为_______.
思考:一次函数y=kx+b的图象与x轴的交点与一元一次方程kx+b=0的根有什么关系?
一次函数y=kx+b的图象与x轴的交点的横坐标就是一元一次方程kx+b=0的根.
-2 0
-2
2 0
2
创设情境,导入新课
现在我们学习了一元二次方程ax2+bx+c=0(a≠0)和二次函数y= ax2+bx+c(a≠0) ,它们之间是否也存在一定的关系呢?本课我们就来学习§2.5 二次函数与一元二次方程 第一课时.
合作探究,展示交流
(1)你的图象与x轴的交点坐标是什么?
(2) 当x取何值时,y=0 ?这里x的取值
与方程有什么关系?
(3) 你能从中得到什么启发?
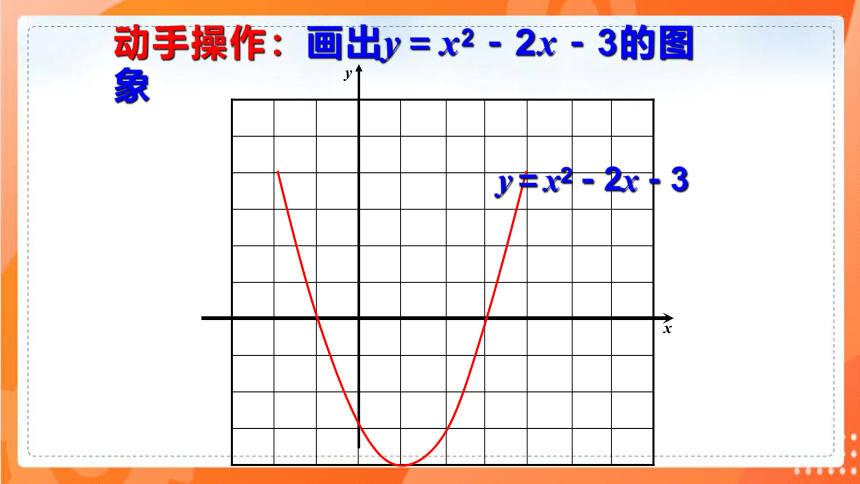
问题:画函数 y=x2-2x-3的图象,根据图象
回答下列问题:
动手操作:画出y=x2-2x-3的图象
x
y
y=x2-2x-3
你的图象与x轴的交点坐标是什么?
函数y=x2-2x-3的图象与x轴两个交点为:
(-1,0)(3,0)。
方程x2-2x-3 =0的两根是:
x1= -1,x2 = 3。
你发现了什么?
(1)二次函数y=ax2+bx+c与x轴的交点的横坐标就是当y=0时一元二次方程ax2+bx+c=0的根。
(2)二次函数的交点问题可以转化为一元二次方程去解决。
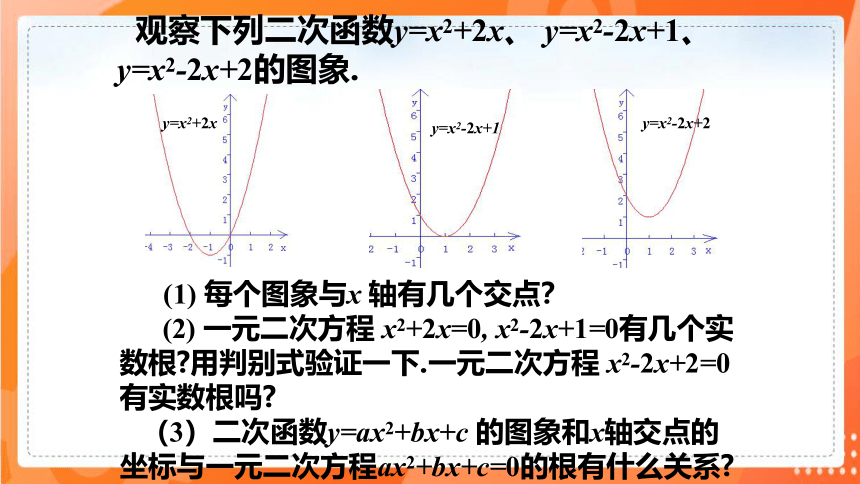
(1) 每个图象与x 轴有几个交点?
(2) 一元二次方程 x2+2x=0, x2-2x+1=0有几个实数根 用判别式验证一下.一元二次方程 x2-2x+2=0 有实数根吗
(3)二次函数y=ax2+bx+c 的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
观察下列二次函数y=x2+2x、 y=x2-2x+1、y=x2-2x+2的图象.
y=x2+2x
y=x2-2x+1
y=x2-2x+2
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点; ②有一个交点;
③没有交点.
与此相对应,一元二次方程ax2+bx+c=0的根也有三种情况:有两个不相等的实数根、有两个相等的实数根、没有实数根.
当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值, 即一元二次方程ax2+bx+c=0的根.
有两个不等的实数根
有两个相等的实数根
没有数学根
有两个交点
有一个交点
没有交点
b2 – 4ac > 0
b2 – 4ac = 0
b2 – 4ac < 0
二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系
ax2+bx+c = 0 的根
y=ax2+bx+c 的图象与x轴的交点
若抛物线 y=ax2+bx+c 与 x 轴有交点,则_____________ .
b2 – 4ac ≥ 0
已知,竖直上抛物体的高度h(m)与运动时间t(s)的关系可用公式
h=-5t2+v0t+h0 表示, 其中h0(m) 是抛出时的高度, v0(m/s)是抛出时的速度.
应用新知,解决问题
h=-5t2+v0t+h0,一个小球从地面以40m/s的速度竖直向上抛起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么:
1.h和t的关系式是?
2.图象上的每一个点的横、纵坐标分别代表什么含义?
3.小球经过多少秒后落地 你有几种求解方法 与同伴进行交流.
h=-5t2+40t.
2 4 6 8
A
B
8s. 可以利用图象,也可以解方程
-5t2+40t=0。
拓展训练, 能力提升
1.二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
A、 a<0, b<0, c>0,b2﹣4ac>0
B、 a >0, b <0, c >0, b2﹣4ac <0
C、 a <0, b >0, c <0, b2﹣4ac >0
D、 a <0, b >0, c >0, b2﹣4ac >0
2.若关于x的函数 与x轴仅有一个公共点,则实数k的值为 —————— .
3.一个足球被从地面向上踢出,它距地面的高度h(m)可以用公式h=-4.9t2+19.6t 来表示.其中t(s)表示足球被踢出后经过的间.
(1)t=1时,足球的高度是多少?
(2)t为何值时,h最大?
(3)球经过多长时间球落地?
(4)方程-4.9t2+19.6t =0的根的实际意义是什么?你能在图上表示吗
(5)方程14.7=-4.9t2+19.6t 的根的实际意义是什么?你能在图上表示吗
(2)∵h=-4.9(t-2) 2+19.6 ∴当t=2时,h最大.
(3)对于h=-4.9t2+19.6t 球落地意味着h=0 即-4.9t2+19.6t=0,解得t1=0(舍去),t2=4 .
即足球被踢出后经过4s后球落地.
(5)解方程 14.7=-4.9t2+19.6t 得t=1, t=3 表明球被踢出1秒和3秒时,离地面的高度都是14.7米图上表示为抛物线与直线h=14.7 的交点的横坐标.
(4) 方程-4.9t2+19.6t =0的根的实际意义是球离地和落地的时间,图上表示为抛物线与x轴交点的横坐 标.
回顾反思,提炼升华
通过这节课的学习,你有哪些收获?有何感想?学会了哪些方法?先想一想,再分享给大家.
课堂小结
二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系:
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c= 0的根 一元二次方程ax2+bx+c= 0根的判别式Δ=b2-4ac
有两个交点
有两个不相等的实数根
只有一个交点
有两个相等的实数根
没有交点
没有实数根
b2 – 4ac > 0
b2 – 4ac = 0
b2 – 4ac < 0
(1)用描点法作二次函数y=x2+2x-10的图象;
你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗?
(2)观察估计二次函数y=x2+2x-10的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,
(3)确定方程x2+2x-10=0的解;
由此可知,方程x2+2x-10=0的近似根为:x1≈-4.3,x2≈2.3.
活动探究
分别约为-4.3和2.3
你认为利用二次函数的图象求一元二次方程的近似根的时候,应该注意什么?
用一元二次方程的求根公式验证一下,看是否有相同的结果
x -4.1 -4.2 -4.3 -4.4
y=x2+2x-10
x 2.1 2.2 2.3 2.4
y=x2+2x-10
其横坐标一个在-5与-4之间
另一个在2与3之间
约为-4.3.
约为2.3.
-1.39
-0.76
-0.11
0.56
-1.39
-0.76
-0.11
0.56
(1)用描点法作二次函数y=x2+2x-10的图象;
利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
做一做
(3)观察估计抛物线y=x2+2x-10和直线y=3的交点的横坐标;
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).
(4)确定方程x2+2x-10=3的解;
由此可知,方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.
(2) 作直线y=3;
(1)原方程可变形为x2+2x-13=0;
利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
(3)观察估计抛物线y=x2+2x-13和x轴的交点的横坐标;
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).
(4)确定方程x2+2x-10=3的解;
由此可知,方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.
(2)用描点法作二次函数y=x2+2x-13的图象;
解法2
利用二次函数y=ax2+bx+c的图象求一元二次方
程ax2+bx+c=0的近似根的一般步骤是怎样的?
课堂点睛
①用描点法作二次函数y=ax2+bx+c的图象;
②观察估计二次函数的图象与x轴的交点的横坐标;
③确定一元二次方程ax2+bx+c=0的解
在求一元二次方程的解的时候,你愿意采用今天学习的这种方法吗?
1.(崇左·中考)二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①abc<0;②方程ax2+bx+c=0的根为x1=
-1,x2=3;③当x>1时,y随x值的增大而减小;④当y>0时,-1<x<3.其中正确的说法是( )
A.① B.①②
C.①②③ D.①②③④
O
x
y
1
3
-1
答案:D
2.(河北·中考)如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A, B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
A.(2,3) B.(3,2)
C.(3,3) D.(4,3)
O
x
y
A
x = 2
B
答案:D
3.(汕头·中考)已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),
与y轴的交点坐标为(0,3).
(1)求出b,c的值,并写出此二次函数的解析式.
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
【解析】(1)由题意得
,解得
故所求解析式为
解得
∴由图象可知,函数值y为正数时,自变量x的取值范围
是-1<x<3.
(2)令
∴抛物线与x轴的另一个交点坐标为(3,0),
4.(株洲·中考)二次函数y=x2-mx+3的图象与x轴的交点如图所示,根据图中信息可得到m的值是_______.
答案:4
5.(咸宁·中考)已知二次函数y=x2+bx-c的图象与x轴两交点的坐标分别为(m,0),(-3m,0)(m≠0).
(1)证明:4c=3b2.
(2)若该函数图象的对称轴为直线x=1,试求二次函数的最小值.
由(1)得
∴二次函数的最小值为-4.
【解析】(1)依题意,m,-3m是一元二次方程
的两根.根据一元二次方程根与系数的
关系,得 ,
∴
,
,
(2)依题意,
,
,
,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版九年级下册数学
第二章 二次函数
2.5二次函数与一元二次方程
创设情境,导入新课
(1)一次函数y=x+2的图象与x轴的交点为( , )
一元一次方程x+2=0的根为_______.
(2) 一次函数y=-3x+6的图象与x轴的交点为( , )
一元一次方程-3x+6=0的根为_______.
思考:一次函数y=kx+b的图象与x轴的交点与一元一次方程kx+b=0的根有什么关系?
一次函数y=kx+b的图象与x轴的交点的横坐标就是一元一次方程kx+b=0的根.
-2 0
-2
2 0
2
创设情境,导入新课
现在我们学习了一元二次方程ax2+bx+c=0(a≠0)和二次函数y= ax2+bx+c(a≠0) ,它们之间是否也存在一定的关系呢?本课我们就来学习§2.5 二次函数与一元二次方程 第一课时.
合作探究,展示交流
(1)你的图象与x轴的交点坐标是什么?
(2) 当x取何值时,y=0 ?这里x的取值
与方程有什么关系?
(3) 你能从中得到什么启发?
问题:画函数 y=x2-2x-3的图象,根据图象
回答下列问题:
动手操作:画出y=x2-2x-3的图象
x
y
y=x2-2x-3
你的图象与x轴的交点坐标是什么?
函数y=x2-2x-3的图象与x轴两个交点为:
(-1,0)(3,0)。
方程x2-2x-3 =0的两根是:
x1= -1,x2 = 3。
你发现了什么?
(1)二次函数y=ax2+bx+c与x轴的交点的横坐标就是当y=0时一元二次方程ax2+bx+c=0的根。
(2)二次函数的交点问题可以转化为一元二次方程去解决。
(1) 每个图象与x 轴有几个交点?
(2) 一元二次方程 x2+2x=0, x2-2x+1=0有几个实数根 用判别式验证一下.一元二次方程 x2-2x+2=0 有实数根吗
(3)二次函数y=ax2+bx+c 的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
观察下列二次函数y=x2+2x、 y=x2-2x+1、y=x2-2x+2的图象.
y=x2+2x
y=x2-2x+1
y=x2-2x+2
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点; ②有一个交点;
③没有交点.
与此相对应,一元二次方程ax2+bx+c=0的根也有三种情况:有两个不相等的实数根、有两个相等的实数根、没有实数根.
当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值, 即一元二次方程ax2+bx+c=0的根.
有两个不等的实数根
有两个相等的实数根
没有数学根
有两个交点
有一个交点
没有交点
b2 – 4ac > 0
b2 – 4ac = 0
b2 – 4ac < 0
二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系
ax2+bx+c = 0 的根
y=ax2+bx+c 的图象与x轴的交点
若抛物线 y=ax2+bx+c 与 x 轴有交点,则_____________ .
b2 – 4ac ≥ 0
已知,竖直上抛物体的高度h(m)与运动时间t(s)的关系可用公式
h=-5t2+v0t+h0 表示, 其中h0(m) 是抛出时的高度, v0(m/s)是抛出时的速度.
应用新知,解决问题
h=-5t2+v0t+h0,一个小球从地面以40m/s的速度竖直向上抛起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么:
1.h和t的关系式是?
2.图象上的每一个点的横、纵坐标分别代表什么含义?
3.小球经过多少秒后落地 你有几种求解方法 与同伴进行交流.
h=-5t2+40t.
2 4 6 8
A
B
8s. 可以利用图象,也可以解方程
-5t2+40t=0。
拓展训练, 能力提升
1.二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
A、 a<0, b<0, c>0,b2﹣4ac>0
B、 a >0, b <0, c >0, b2﹣4ac <0
C、 a <0, b >0, c <0, b2﹣4ac >0
D、 a <0, b >0, c >0, b2﹣4ac >0
2.若关于x的函数 与x轴仅有一个公共点,则实数k的值为 —————— .
3.一个足球被从地面向上踢出,它距地面的高度h(m)可以用公式h=-4.9t2+19.6t 来表示.其中t(s)表示足球被踢出后经过的间.
(1)t=1时,足球的高度是多少?
(2)t为何值时,h最大?
(3)球经过多长时间球落地?
(4)方程-4.9t2+19.6t =0的根的实际意义是什么?你能在图上表示吗
(5)方程14.7=-4.9t2+19.6t 的根的实际意义是什么?你能在图上表示吗
(2)∵h=-4.9(t-2) 2+19.6 ∴当t=2时,h最大.
(3)对于h=-4.9t2+19.6t 球落地意味着h=0 即-4.9t2+19.6t=0,解得t1=0(舍去),t2=4 .
即足球被踢出后经过4s后球落地.
(5)解方程 14.7=-4.9t2+19.6t 得t=1, t=3 表明球被踢出1秒和3秒时,离地面的高度都是14.7米图上表示为抛物线与直线h=14.7 的交点的横坐标.
(4) 方程-4.9t2+19.6t =0的根的实际意义是球离地和落地的时间,图上表示为抛物线与x轴交点的横坐 标.
回顾反思,提炼升华
通过这节课的学习,你有哪些收获?有何感想?学会了哪些方法?先想一想,再分享给大家.
课堂小结
二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系:
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c= 0的根 一元二次方程ax2+bx+c= 0根的判别式Δ=b2-4ac
有两个交点
有两个不相等的实数根
只有一个交点
有两个相等的实数根
没有交点
没有实数根
b2 – 4ac > 0
b2 – 4ac = 0
b2 – 4ac < 0
(1)用描点法作二次函数y=x2+2x-10的图象;
你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗?
(2)观察估计二次函数y=x2+2x-10的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,
(3)确定方程x2+2x-10=0的解;
由此可知,方程x2+2x-10=0的近似根为:x1≈-4.3,x2≈2.3.
活动探究
分别约为-4.3和2.3
你认为利用二次函数的图象求一元二次方程的近似根的时候,应该注意什么?
用一元二次方程的求根公式验证一下,看是否有相同的结果
x -4.1 -4.2 -4.3 -4.4
y=x2+2x-10
x 2.1 2.2 2.3 2.4
y=x2+2x-10
其横坐标一个在-5与-4之间
另一个在2与3之间
约为-4.3.
约为2.3.
-1.39
-0.76
-0.11
0.56
-1.39
-0.76
-0.11
0.56
(1)用描点法作二次函数y=x2+2x-10的图象;
利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
做一做
(3)观察估计抛物线y=x2+2x-10和直线y=3的交点的横坐标;
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).
(4)确定方程x2+2x-10=3的解;
由此可知,方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.
(2) 作直线y=3;
(1)原方程可变形为x2+2x-13=0;
利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
(3)观察估计抛物线y=x2+2x-13和x轴的交点的横坐标;
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).
(4)确定方程x2+2x-10=3的解;
由此可知,方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.
(2)用描点法作二次函数y=x2+2x-13的图象;
解法2
利用二次函数y=ax2+bx+c的图象求一元二次方
程ax2+bx+c=0的近似根的一般步骤是怎样的?
课堂点睛
①用描点法作二次函数y=ax2+bx+c的图象;
②观察估计二次函数的图象与x轴的交点的横坐标;
③确定一元二次方程ax2+bx+c=0的解
在求一元二次方程的解的时候,你愿意采用今天学习的这种方法吗?
1.(崇左·中考)二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①abc<0;②方程ax2+bx+c=0的根为x1=
-1,x2=3;③当x>1时,y随x值的增大而减小;④当y>0时,-1<x<3.其中正确的说法是( )
A.① B.①②
C.①②③ D.①②③④
O
x
y
1
3
-1
答案:D
2.(河北·中考)如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A, B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
A.(2,3) B.(3,2)
C.(3,3) D.(4,3)
O
x
y
A
x = 2
B
答案:D
3.(汕头·中考)已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),
与y轴的交点坐标为(0,3).
(1)求出b,c的值,并写出此二次函数的解析式.
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
【解析】(1)由题意得
,解得
故所求解析式为
解得
∴由图象可知,函数值y为正数时,自变量x的取值范围
是-1<x<3.
(2)令
∴抛物线与x轴的另一个交点坐标为(3,0),
4.(株洲·中考)二次函数y=x2-mx+3的图象与x轴的交点如图所示,根据图中信息可得到m的值是_______.
答案:4
5.(咸宁·中考)已知二次函数y=x2+bx-c的图象与x轴两交点的坐标分别为(m,0),(-3m,0)(m≠0).
(1)证明:4c=3b2.
(2)若该函数图象的对称轴为直线x=1,试求二次函数的最小值.
由(1)得
∴二次函数的最小值为-4.
【解析】(1)依题意,m,-3m是一元二次方程
的两根.根据一元二次方程根与系数的
关系,得 ,
∴
,
,
(2)依题意,
,
,
,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
