2021-2022学年人教版初中数学七年级上册4.2 比较线段的长短 课件(共39张PPT)
文档属性
| 名称 | 2021-2022学年人教版初中数学七年级上册4.2 比较线段的长短 课件(共39张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 771.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-30 19:46:58 | ||
图片预览








文档简介
(共39张PPT)
比较线段的大小
学习目标
1.掌握线段的性质
2.能比较两条线段的大小
3.会用尺规作图
4.了解线段中点的定义及其运用
回顾思考:
直线的特点、表示方法?
线段的特点、表示方法?
射线的特点、表示方法?
如图从A村到B村,有三条路径可选择你愿意选第几条路径?说出你的理由。
A
B
想一想:
线段的性质:
两点之间的所有连线中,线段最短.
也可简述为:“两点之间线段最短。”
结论
注意:
两点之间的距离是一个实际的长度(非负数),一定要带单位。
两点间的距离:
两点之间线段的长度。
小狗、小猫为什么都选择直的路?
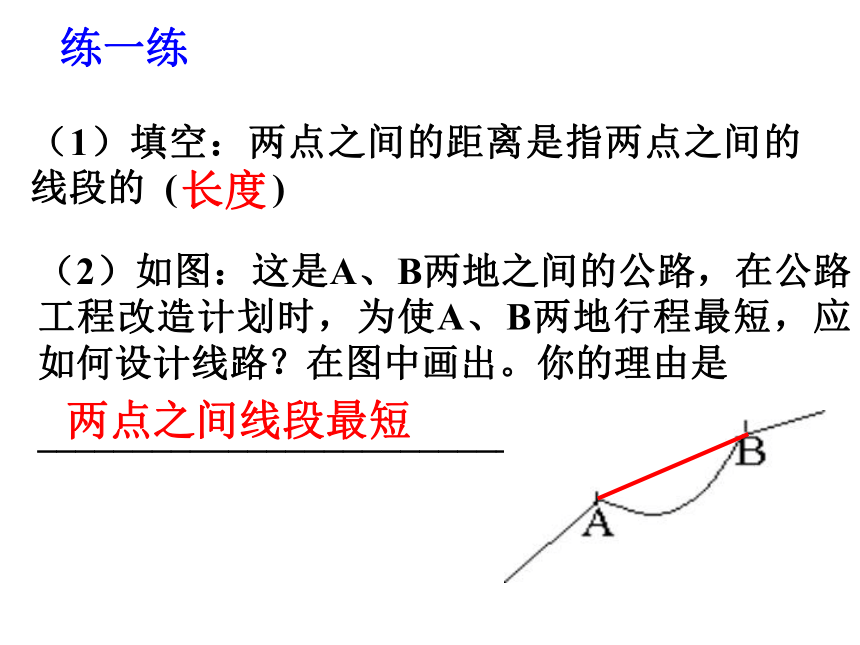
(2)如图:这是A、B两地之间的公路,在公路工程改造计划时,为使A、B两地行程最短,应如何设计线路?在图中画出。你的理由是
_______________________________
练一练
长度
两点之间线段最短
(1)填空:两点之间的距离是指两点之间的线段的 ( )
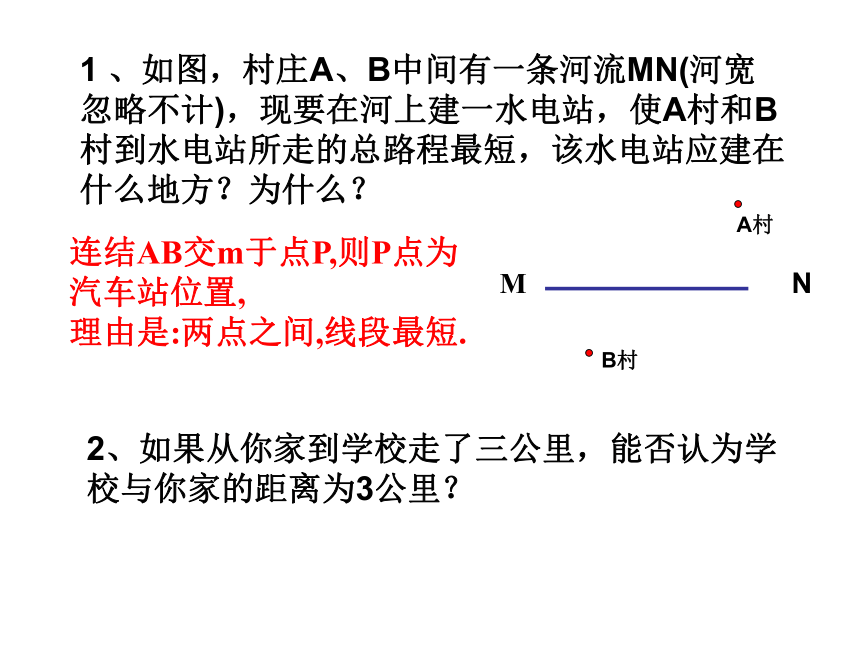
1 、如图,村庄A、B中间有一条河流MN(河宽忽略不计),现要在河上建一水电站,使A村和B村到水电站所走的总路程最短,该水电站应建在什么地方?为什么?
2、如果从你家到学校走了三公里,能否认为学校与你家的距离为3公里?
B村
M N
A村
连结AB交m于点P,则P点为汽车站位置,
理由是:两点之间,线段最短.
例1:在线段AB上有一点M,若AB=6cm,AM=2cm,则点M与点B之间的距离是多少?
解:∵AB=6cm,AM=2cm,
∴MB=AB-AM=6-2=4cm
即点M与点B之间的距离为4cm。
1、如果线段AB=5cm,线段BC=4cm,那么A,C两点之间的距离是( )
A. 9cm B.1cm
C.1cm或9cm D.以上答案都不对
C
拓展应用
B
问题(2) 你如何比较两根筷子的长短?
问题(3) 怎样比较两条线段的长短呢?
问题(1) 两名同学如何比个儿?
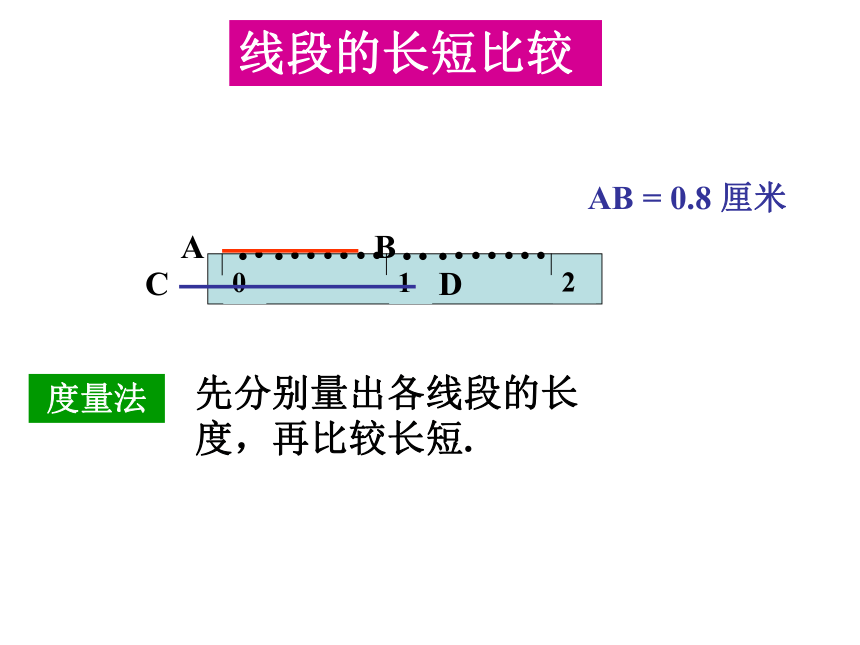
线段的长短比较
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
0
1
2
AB = 0.8 厘米
A
B
C
D
度量法
先分别量出各线段的长度,再比较长短.
线段的长短比较
A
B
C
D
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
0
1
2
AB = 0.8 厘米
CD = 1.4 厘米
度量法
先分别量出各线段的长度,再比较长短.
线段的长短比较
A
B
C
D
AB = 0.8 厘米
CD = 1.4 厘米
∴ AB<CD
或 CD>AB
度量法
先分别量出各线段的长度,再比较长短.
线段的大小比较
叠合法
将线段重叠在一起,使一个端点重合,再进行比较.
线段的长短比较
A
B
C
D
叠合法
将线段重叠在一起,使一个端点重合,再进行比较.
线段的长短比较
A
B
C
D
叠合法
将线段重叠在一起,使一个端点重合,再进行比较.
C
如何用直尺、圆规画一条线段等于已知线段?
第一步:先用直尺画一条射线AB.
第二步:用圆规量出已知线段的长度.
第三步:在射线AB上以A为圆心,已知线段的长度为半径画弧,交射线AB于点C,
则线段AC就是所求作的线段。
A
B
三步骤:
1、画射线
2、度量已知线段
3、在射线上画弧
已知线段a,b,请用圆规、直尺做一条线段AB ,
(1)使线段AB=a+b
(2)使线段AB=a-b
(3)使线段AB=2a
(4)使线段AB=2a-b
练习:
A
B
M
A
B
M
A
B
M
A
B
M
A
B
M
A
B
M
A
B
M
A
B
M
A
B
M
A
B
M
A
(B)
M
A
B
M
A
B
M
把一条线段分成两条相等线段的点,叫做这条线段的中点
几何语言:
∵点M是线段AB的中点
∴
或∴AB=2AM=2BM
判断:
若AM=BM,则M为线段AB的中点。
线段中点的条件:
1、在已知线段上。
2、把已知线段分成两条相等线段的点
A
B
M
练习
1.已知线段AB,点C是线段AB的中点,AB=6cm,求线段BC的长。
2.已知线段AB,点C是线段AB的中点,BC=8cm,求线段AB的长。
A
B
C
A
B
C
3、如图,AB=8㎝,CB=5㎝,D是AC的中点,求DC的长。
解:∵ AB=8㎝,CB=5㎝
∴ AC=____—____ (表示出线段和差)
=__________
∵ D是AC的中点
∴ DC=_______=_______
4、如图,AB = 6cm,点C是线段AB的中点,点D是线段BC的中点,求线段AD的长.
.
.
.
.
A
C
D
B
6厘米
?厘米
解:∵ 点C是线段AB的中点,AB=6cm
∴ AC = BC = AB
= 3cm
∵ 点D是线段BC的中点,
∴ CD = BC
= 1.5cm
∴ AD = AC + CD
= 3 + 1.5
= 4.5cm
5、己知,如图,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点,如果AB=10cm,AC=6cm,求CN、MN的长。
6、 在直线a上顺次截取A,B,C三点,使得 AB=4cm,BC=3cm.如果O是线段AC的中点,求线段OB的长。
※ 变式:如果将题中的“顺次”去掉,又会是怎样的结果呢?请思考。
这节课你学会了什么?
1.线段的基本性质:两点之间线段最短。
2.两点之间的距离:两点之间线段的长度。
3.线段的两种比较方法:叠合法和度量法。
4.线段的中点的概念及表示方法。
1、下列图形能比较大小的是( )
A、直线与线段
B、直线与射线
C、两条线段
D、射线与线段
练习:
c
(2)如图 AB=6cm,点C是AB的中点,点D是CB的中点,则AD=____cm
(3)如图,下列说法 ,不能判断点C是线段AB的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB= AB
C
4.5
5.有A、B、C三城市,已知A、B两市的距离为50千米,B、C两市的距离是30千米,那么A、C两市间的距离是( )
(A)80千米 (B)20千米
(C)40千米 (D)处于20千米~80千米之间
D
4. 如图,BC=4 cm,BD=7 cm , D是AC的中点,则AC= cm, AB= cm
6
10
如图,点C是线段AB上任意一点,点D是线段AC的中点,点E是线段BC的中点,则线段DE和线段AB有怎样的关系?说明理由.
.
.
A
B
.
C
.
.
D
E
DE = AB
解:
∵点D是线段AC的中点
∴ DC = AC
∵点E是线段BC的中点
∴ CE = BC
∴ DE
= DC + CE
= AC + BC
= (AC + BC)
= AB
理由如下:
已知:如图,B、C两点把线段AD分成2:4:3三部分,M是AD的中点,CD=6, 求线段MC的长.
比较线段的大小
学习目标
1.掌握线段的性质
2.能比较两条线段的大小
3.会用尺规作图
4.了解线段中点的定义及其运用
回顾思考:
直线的特点、表示方法?
线段的特点、表示方法?
射线的特点、表示方法?
如图从A村到B村,有三条路径可选择你愿意选第几条路径?说出你的理由。
A
B
想一想:
线段的性质:
两点之间的所有连线中,线段最短.
也可简述为:“两点之间线段最短。”
结论
注意:
两点之间的距离是一个实际的长度(非负数),一定要带单位。
两点间的距离:
两点之间线段的长度。
小狗、小猫为什么都选择直的路?
(2)如图:这是A、B两地之间的公路,在公路工程改造计划时,为使A、B两地行程最短,应如何设计线路?在图中画出。你的理由是
_______________________________
练一练
长度
两点之间线段最短
(1)填空:两点之间的距离是指两点之间的线段的 ( )
1 、如图,村庄A、B中间有一条河流MN(河宽忽略不计),现要在河上建一水电站,使A村和B村到水电站所走的总路程最短,该水电站应建在什么地方?为什么?
2、如果从你家到学校走了三公里,能否认为学校与你家的距离为3公里?
B村
M N
A村
连结AB交m于点P,则P点为汽车站位置,
理由是:两点之间,线段最短.
例1:在线段AB上有一点M,若AB=6cm,AM=2cm,则点M与点B之间的距离是多少?
解:∵AB=6cm,AM=2cm,
∴MB=AB-AM=6-2=4cm
即点M与点B之间的距离为4cm。
1、如果线段AB=5cm,线段BC=4cm,那么A,C两点之间的距离是( )
A. 9cm B.1cm
C.1cm或9cm D.以上答案都不对
C
拓展应用
B
问题(2) 你如何比较两根筷子的长短?
问题(3) 怎样比较两条线段的长短呢?
问题(1) 两名同学如何比个儿?
线段的长短比较
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
0
1
2
AB = 0.8 厘米
A
B
C
D
度量法
先分别量出各线段的长度,再比较长短.
线段的长短比较
A
B
C
D
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
0
1
2
AB = 0.8 厘米
CD = 1.4 厘米
度量法
先分别量出各线段的长度,再比较长短.
线段的长短比较
A
B
C
D
AB = 0.8 厘米
CD = 1.4 厘米
∴ AB<CD
或 CD>AB
度量法
先分别量出各线段的长度,再比较长短.
线段的大小比较
叠合法
将线段重叠在一起,使一个端点重合,再进行比较.
线段的长短比较
A
B
C
D
叠合法
将线段重叠在一起,使一个端点重合,再进行比较.
线段的长短比较
A
B
C
D
叠合法
将线段重叠在一起,使一个端点重合,再进行比较.
C
如何用直尺、圆规画一条线段等于已知线段?
第一步:先用直尺画一条射线AB.
第二步:用圆规量出已知线段的长度.
第三步:在射线AB上以A为圆心,已知线段的长度为半径画弧,交射线AB于点C,
则线段AC就是所求作的线段。
A
B
三步骤:
1、画射线
2、度量已知线段
3、在射线上画弧
已知线段a,b,请用圆规、直尺做一条线段AB ,
(1)使线段AB=a+b
(2)使线段AB=a-b
(3)使线段AB=2a
(4)使线段AB=2a-b
练习:
A
B
M
A
B
M
A
B
M
A
B
M
A
B
M
A
B
M
A
B
M
A
B
M
A
B
M
A
B
M
A
(B)
M
A
B
M
A
B
M
把一条线段分成两条相等线段的点,叫做这条线段的中点
几何语言:
∵点M是线段AB的中点
∴
或∴AB=2AM=2BM
判断:
若AM=BM,则M为线段AB的中点。
线段中点的条件:
1、在已知线段上。
2、把已知线段分成两条相等线段的点
A
B
M
练习
1.已知线段AB,点C是线段AB的中点,AB=6cm,求线段BC的长。
2.已知线段AB,点C是线段AB的中点,BC=8cm,求线段AB的长。
A
B
C
A
B
C
3、如图,AB=8㎝,CB=5㎝,D是AC的中点,求DC的长。
解:∵ AB=8㎝,CB=5㎝
∴ AC=____—____ (表示出线段和差)
=__________
∵ D是AC的中点
∴ DC=_______=_______
4、如图,AB = 6cm,点C是线段AB的中点,点D是线段BC的中点,求线段AD的长.
.
.
.
.
A
C
D
B
6厘米
?厘米
解:∵ 点C是线段AB的中点,AB=6cm
∴ AC = BC = AB
= 3cm
∵ 点D是线段BC的中点,
∴ CD = BC
= 1.5cm
∴ AD = AC + CD
= 3 + 1.5
= 4.5cm
5、己知,如图,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点,如果AB=10cm,AC=6cm,求CN、MN的长。
6、 在直线a上顺次截取A,B,C三点,使得 AB=4cm,BC=3cm.如果O是线段AC的中点,求线段OB的长。
※ 变式:如果将题中的“顺次”去掉,又会是怎样的结果呢?请思考。
这节课你学会了什么?
1.线段的基本性质:两点之间线段最短。
2.两点之间的距离:两点之间线段的长度。
3.线段的两种比较方法:叠合法和度量法。
4.线段的中点的概念及表示方法。
1、下列图形能比较大小的是( )
A、直线与线段
B、直线与射线
C、两条线段
D、射线与线段
练习:
c
(2)如图 AB=6cm,点C是AB的中点,点D是CB的中点,则AD=____cm
(3)如图,下列说法 ,不能判断点C是线段AB的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB= AB
C
4.5
5.有A、B、C三城市,已知A、B两市的距离为50千米,B、C两市的距离是30千米,那么A、C两市间的距离是( )
(A)80千米 (B)20千米
(C)40千米 (D)处于20千米~80千米之间
D
4. 如图,BC=4 cm,BD=7 cm , D是AC的中点,则AC= cm, AB= cm
6
10
如图,点C是线段AB上任意一点,点D是线段AC的中点,点E是线段BC的中点,则线段DE和线段AB有怎样的关系?说明理由.
.
.
A
B
.
C
.
.
D
E
DE = AB
解:
∵点D是线段AC的中点
∴ DC = AC
∵点E是线段BC的中点
∴ CE = BC
∴ DE
= DC + CE
= AC + BC
= (AC + BC)
= AB
理由如下:
已知:如图,B、C两点把线段AD分成2:4:3三部分,M是AD的中点,CD=6, 求线段MC的长.
