2022届高三数学选填专题练习-培优冲刺(Word含答案解析)
文档属性
| 名称 | 2022届高三数学选填专题练习-培优冲刺(Word含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 18:32:19 | ||
图片预览



文档简介
高三数学选填专题练习(33)
培优冲刺(3)
难度评估:困难 测试时间:60分钟
一、单选题(共60分)
1.(本题5分)已知集合,,定义集合,则中元素的个数为( )
A.77 B.49 C.45 D.30
2.(本题5分)设复数在复平面内的对应点关于虚轴对称,,则
A.-5 B.5 C. D.
3.(本题5分)设函数在区间上单调,且,当时,取到最大值2,若将函数的图像上各点的横坐标伸长为原来的2倍得到函数的图像,则不等式的解集为( )
A. B.
C. D.
4.(本题5分)如图,为的外接圆的直径,若,且,则( )
A.2 B. C.1 D.
5.(本题5分)现有4个人通过掷一枚质地均匀的骰子去参加篮球和乒乓球的体育活动,掷出点数为1或2的人去打篮球,擦出点数大于2的人去打乒乓球.用,分别表示这4个人中去打篮球和乒乓球的人数,记,求随机变量的数学期望为( )
A. B. C. D.
6.(本题5分)北宋数学家沈括博学多才、善于观察.据说有一天,他走进一家酒馆,看到一层层垒起来的酒坛(如图所示),不禁想到:“怎么求这些酒坛的总数呢?”“后来沈括提出了“隙积术”,相当于求数列的和.如图,最上层的小球数是20,其中,则这堆小球总数不可能是( )
A.1100 B.5200 C.8100 D.21300
7.(本题5分)已知函数的图象与函数的图象有且仅有两个不同的公共点,则实数的取值范围是( )
A. B. C. D.
8.(本题5分)若抛物线的焦点为F,点A、B在抛物线上,且,弦AB的中点M在准线l上的射影为,则的最大值为( )
A. B. C. D.
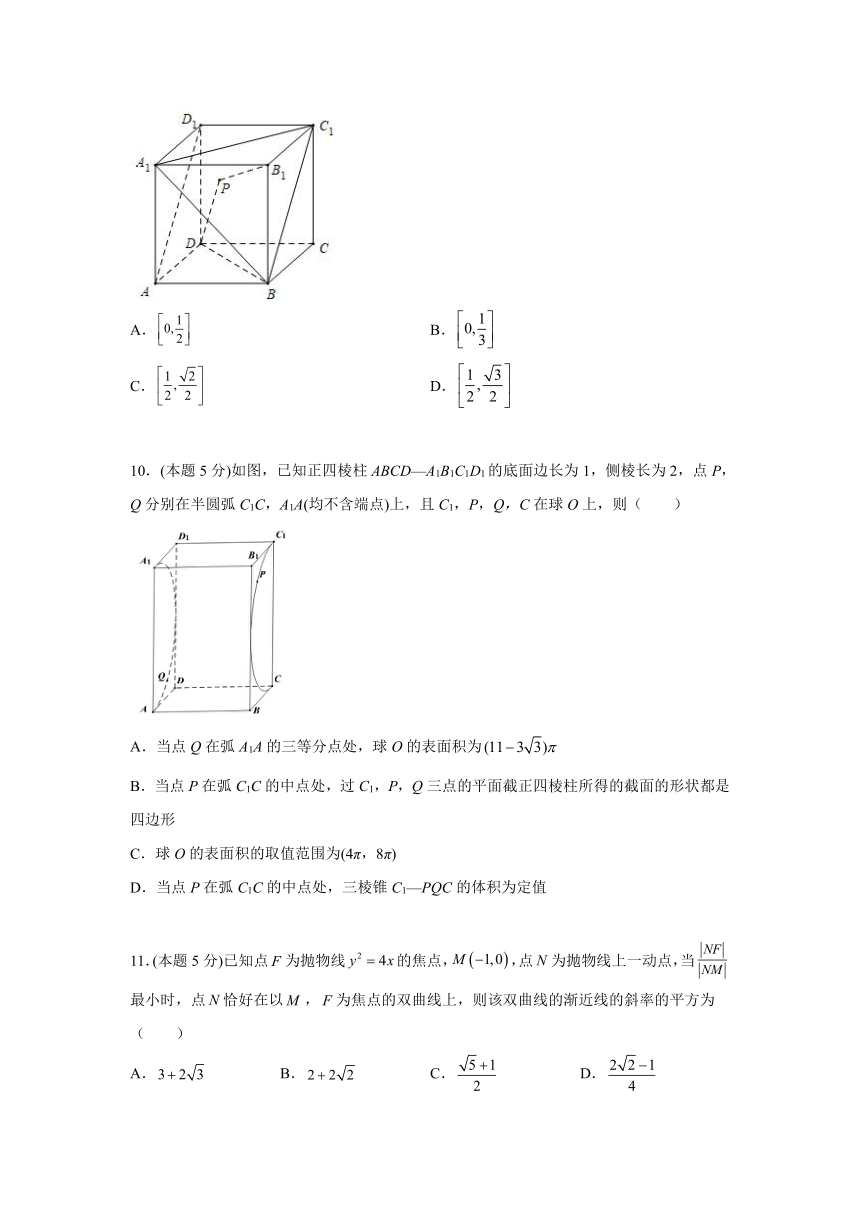
9.(本题5分)如图,在棱长为的正方体中,点是平面内一个动点,且满足,则直线与直线所成角的余弦值的取值范围为( )
A. B.
C. D.
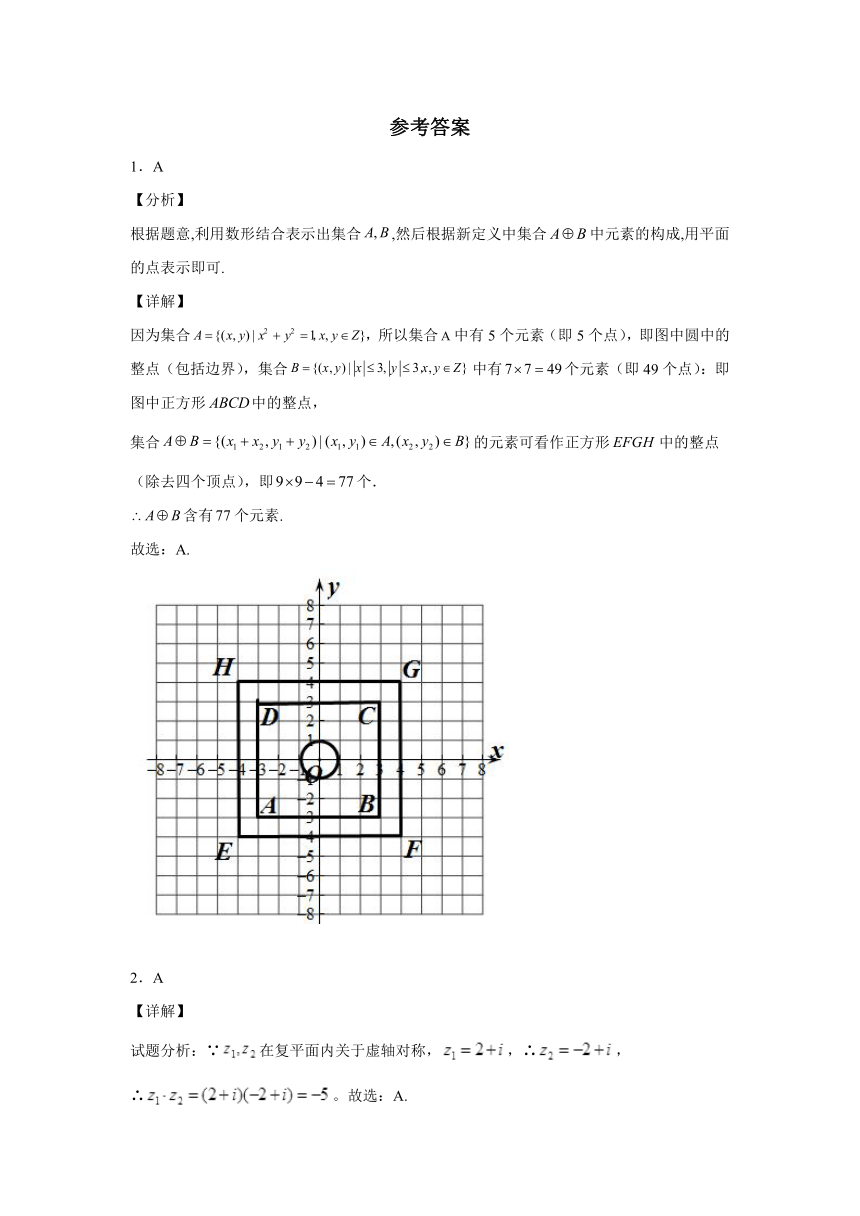
10.(本题5分)如图,已知正四棱柱ABCD—A1B1C1D1的底面边长为1,侧棱长为2,点P,Q分别在半圆弧C1C,A1A(均不含端点)上,且C1,P,Q,C在球O上,则( )
A.当点Q在弧A1A的三等分点处,球O的表面积为
B.当点P在弧C1C的中点处,过C1,P,Q三点的平面截正四棱柱所得的截面的形状都是四边形
C.球O的表面积的取值范围为(4π,8π)
D.当点P在弧C1C的中点处,三棱锥C1—PQC的体积为定值
11.(本题5分)已知点为抛物线的焦点,,点为抛物线上一动点,当最小时,点恰好在以,为焦点的双曲线上,则该双曲线的渐近线的斜率的平方为( )
A. B. C. D.
12.(本题5分)已知定义在上的函数的导函数为,满足.当时,.当时,,且,其中是自然对数的底数.则的取值范围为( )
A. B. C. D.
二、填空题(共20分)
13.(本题5分)正方形的边长为2,圆内切于正方形,为圆的一条动直径,点为正方形边界上任一点,则的取值范围是______.
14.(本题5分)在平面上,将两个半圆弧和、两条直线和围成的封闭图形记为,如图中阴影部分.记绕轴旋转一周而成的几何体为,过作的水平截面,所得截面面积为,试利用祖暅原理(祖暅原理:“幂势既同,则积不容异”,意思是:两等高的几何体在同高处被截得的两个截面面积均相等,那么这两个几何体的体积相等)、一个平放的圆柱和一个长方体,得出的体积值为__________.
(本题5分)设△AnBnCn的三边长分别为an,bn,cn,n=1,2,3…,若,,,,则的最大值是________________.
(本题5分)某校高二年级共有10个班级,5位教学教师,每位教师教两个班级,其中姜老师一定教1班,张老师一定教3班,王老师一定教8班,秋老师至少教9班和10班中的一个班,曲老师不教2班和6班,王老师不教5班,则不同的排课方法种数______.
参考答案
1.A
【分析】
根据题意,利用数形结合表示出集合,然后根据新定义中集合中元素的构成,用平面的点表示即可.
【详解】
因为集合,所以集合中有5个元素(即5个点),即图中圆中的整点(包括边界),集合中有个元素(即49个点):即图中正方形中的整点,
集合的元素可看作正方形中的整点(除去四个顶点),即个.
含有个元素.
故选:A.
2.A
【详解】
试题分析:∵在复平面内关于虚轴对称,,∴,∴。故选:A.
3.A
【分析】
首先设函数,由条件确定周期和的范围,再利用对称性求出对称中心和对称轴,求,代入求,利用伸缩变换求,最后解不等式.
【详解】
函数的最大值为2,,
在区间上单调,所以,即,
,即,
,是函数的对称轴,
,是函数的对称中心,
和是函数相邻的对称轴和对称中心,,得,
当时,取到最大值2,,,
当时,,
,根据题意可知,
,
,解得:,.
的解集是.
故选:A.
4.C
【分析】
作于点E,于点M,根据平面向量的定义,结合锐角三角函数的定义、垂径定理、平面向量的几何意义进行求解即可.
【详解】
作图如下:
由题意得:作于点E,于点M,因为,即:所以,又因为,
所以.即.
又因为,所以 ,所以.即 在上的投影为.
.
故选:C.
5.D
【分析】
分别求出每个人去打篮球、打乒乓球的概率,的所有可能取值为0,2,4,利用二项分布的概率公式求出的分布列即可求得的期望值.
【详解】
依题意,这4个人中,每个人去打篮球的概率为,去打乒乓球的概率为,
设“这4个人中恰有人去打篮球”为事件,
则﹐的所有可能取值为0,2,4.
由于与互斥﹐与互斥,故﹐
,
所以的分布列为
2 2 4
随机变量ξ的数学期望.
故选:D.
6.B
【分析】
先用组合数的性质求和得,再逐一验证即可
【详解】
因为,
令,,
令的前项和为,
则
,
对于A:,
则,解得,故A有可能;
对于B:,
则,
因为,
故无正整数解,故B不可能;
对于C:,
则,解得,故C有可能;
对于D:,
则,解得,故D有可能;
故选:B.
7.A
【分析】
令,根据条件可知有两个不同的零点,然后分三种情况,求出k的取值范围.
【详解】
解:令,则,
∵和图象有且仅有两个不同的公共点,∴有两个不同的零点,
又,
当时,在上单调递增,在上单调递减,且,
∴图象的左右两边向下无限延伸,故此时有两个零点,∴满足题意;
当时,只有一个零点,不滿足题意;
当时,,在上单调递增,在上单调递减,在上单调递增,且,
易知只有一个零点,不满足题意;
综上,的取值范围是.
故选:A.
8.C
【分析】
转化:,利用余弦定理:,即得解.
【详解】
如图所示,由题意得,
当且仅当:时,有最大值.
故选:C.
9.A
【分析】
求得点的轨迹是平面内以点为圆心,半径为的圆,可得,进而可得出题中所求角等于直线与直线的夹角,然后过点作平面于点,过点作于点,连接,找出使得最大和最小时的位置,进而可求得所求角的余弦值的取值范围.
【详解】
连接交平面于点,延长线段至点,使得,连接、、,如下图所示:
已知在正方体中,底面,平面,,
又四边形为正方形,所以,,
,平面,平面,,
同理,,平面,
三棱锥的体积为,
,,
可得,
所以,线段的长被平面与平面三等分,且与两平面分别垂直,
而正方体的棱长为,所以,,如下图所示:
其中,不妨设,由题意可,
所以,,可得,
所以,点在平面内以点为圆心,半径为的圆上.
因为,所以,直线与直线的夹角即为直线与直线所成角.
接下来要求出线段与的长,然后在中利用余弦定理求解.
如图,过点作平面于点,过点作于点,连接,
根据题意可知,,且,
所以,,.
如图所示,,当点在处时,最大,当点在处时,最小.
这两种情况下直线与直线夹角的余弦值最大,为;
当点在点处时,为直角,此时余弦值最小为.
综上所述,直线与直线所成角的余弦值的取值范围是.
故选:A.
10.D
【分析】
取中点,中点,中点,根据球的性质,容易知道球心O在线段EF上,设出OE的长度和∠FGQ,算出FQ的长度,利用OC1=OQ,即可判断A,B;
作出过C1,P,Q三点的截面即可判断C;
利用即可求出体积,进而判断D.
【详解】
如图1,取中点,中点,中点,由题意,球心在线段上,设,在中,由余项定理,设,
则,∴,
设外接球半径为R,∵,∴,
∴,∴,∴球的表面积,C错误;
当点Q在的三等分点处,,则,,∴∴球的表面积,A错误;
对B,如图2,取中点,当在上时,连接AF,在平面ADD1A1上过点Q作AF的平行线,与线段,AD分别交于M,N,延长C1P与BC交于R,连接RN交AB于S,此时截面为,B错误;
对D,当点P位于的中点处,三棱锥的体积为定值,D正确.
故选:D.
11.B
【分析】
作出图形,可知与抛物线相切时,取得最小值,求出点的坐标,利用双曲线定义求出2a,结合,可求得,再利用求得结果.
【详解】
由抛物线的对称性,设为抛物线第一象限内点,如图所示:
故点作垂直于抛物线的准线于点B,由抛物线的定义知,易知轴,可得
当取得最大值时,取得最小值,此时与抛物线相切,
设直线方程为:,
联立,整理得,
其中,解得:,由为抛物线第一象限内点,则
则,解得:,此时,即或
所以点的坐标且
由题意知,双曲线的左焦点为,右焦点为
设双曲线的实轴长为2a,则,,
又,则
故渐近线斜率的平方为
故选:B.
12.B
【分析】
根据题意,构造函数和,对于,由题意可得,利用导数分析可得在区间上单调递增,进而有,对其变形可得,同理分析的单调性可得,综合即可得答案.
【详解】
根据题意,设,(),,()
∵,∴,
即,∴
对于,其导数,
∵,,则有在区间上单调递增;
所以,即,变形可得;
对于,其导数,
∵时,,则在区间上单调递减;
则有,即,变形可得,
综合可得:,即的范围为.
故选:B.
13.
【分析】
根据向量关系表示,只需求出的取值范围即可得解.
【详解】
由题可得:,
故答案为:
14.
【分析】
由题目给出的的水平截面的面积,可猜想水平放置的圆柱和长方体的量,然后直接求出圆柱的体积与长方体的体积作和即可.
【详解】
因为几何体的水平截面的截面面积为,该截面的截面面积由两部分组成,一部分为定值,看作是截一个底面积为,高为2的长方体得到的,对于,看作是把一个半径为1,高为的圆柱得到的,如图所示:
这两个几何体和放在一起,根据祖暅原理,每个平行水平面的截面面积相等,故它们体积相等,即的体积为。故填:.
15.
【分析】
根据题干条件得到,进而利用余弦定理及基本不等式求出,从而求出的最大值是.
【详解】
由,得:,
又,所以,,所以,所以
,当且仅当时等号成立,此时三角形为等边三角形,所以的最大值是.
故答案为:.
16.236
【分析】
按照特殊元素优先处理原则,分类讨论秋老师教9班,秋老师教10班的排课方法种数,但这两种重复了秋老师同时教9班和10班的排课方法种数,减去即可得到答案.
【详解】
(1)秋老师教9班,曲老师可在4,5,7,10班中选两班,再分两小类:
①曲老师不教5班,则曲老师可选(种);王老师可选(种);剩余的3个班3个老师全排列安排有(种);按分步相乘计数原理有:(种);
②曲老师教5班,则曲老师可选(种);剩余的4个班4个老师全排列安排有(种);按分步相乘计数原理有:(种).
按分类相加计数原理,秋老师教9班有:(种);
(2)秋老师教10班,同理也有126(种);
(3)秋老师同时教9班和10班,曲老师可在4,5,7班中选两班,再分两小类:
①曲老师不教5班,则曲老师教4班和7班,王老师再从2,6班选一个,可选(种);剩余的2个班2个老师全排列安排有(种);按分步相乘计数原理有:(种);
②曲老师教5班,则曲老师可选(种);剩余的3个班3个老师全排列安排有(种);按分步相乘计数原理有:(种).
按分类相加计数原理,秋老师同时教9班和10班有:(种);
但秋老师同时教9班和10班在(1)和(2)两种分类里都涉及到,所以重复需减去,
故不同的排课方法种数有:(种).
故答案为:236.
培优冲刺(3)
难度评估:困难 测试时间:60分钟
一、单选题(共60分)
1.(本题5分)已知集合,,定义集合,则中元素的个数为( )
A.77 B.49 C.45 D.30
2.(本题5分)设复数在复平面内的对应点关于虚轴对称,,则
A.-5 B.5 C. D.
3.(本题5分)设函数在区间上单调,且,当时,取到最大值2,若将函数的图像上各点的横坐标伸长为原来的2倍得到函数的图像,则不等式的解集为( )
A. B.
C. D.
4.(本题5分)如图,为的外接圆的直径,若,且,则( )
A.2 B. C.1 D.
5.(本题5分)现有4个人通过掷一枚质地均匀的骰子去参加篮球和乒乓球的体育活动,掷出点数为1或2的人去打篮球,擦出点数大于2的人去打乒乓球.用,分别表示这4个人中去打篮球和乒乓球的人数,记,求随机变量的数学期望为( )
A. B. C. D.
6.(本题5分)北宋数学家沈括博学多才、善于观察.据说有一天,他走进一家酒馆,看到一层层垒起来的酒坛(如图所示),不禁想到:“怎么求这些酒坛的总数呢?”“后来沈括提出了“隙积术”,相当于求数列的和.如图,最上层的小球数是20,其中,则这堆小球总数不可能是( )
A.1100 B.5200 C.8100 D.21300
7.(本题5分)已知函数的图象与函数的图象有且仅有两个不同的公共点,则实数的取值范围是( )
A. B. C. D.
8.(本题5分)若抛物线的焦点为F,点A、B在抛物线上,且,弦AB的中点M在准线l上的射影为,则的最大值为( )
A. B. C. D.
9.(本题5分)如图,在棱长为的正方体中,点是平面内一个动点,且满足,则直线与直线所成角的余弦值的取值范围为( )
A. B.
C. D.
10.(本题5分)如图,已知正四棱柱ABCD—A1B1C1D1的底面边长为1,侧棱长为2,点P,Q分别在半圆弧C1C,A1A(均不含端点)上,且C1,P,Q,C在球O上,则( )
A.当点Q在弧A1A的三等分点处,球O的表面积为
B.当点P在弧C1C的中点处,过C1,P,Q三点的平面截正四棱柱所得的截面的形状都是四边形
C.球O的表面积的取值范围为(4π,8π)
D.当点P在弧C1C的中点处,三棱锥C1—PQC的体积为定值
11.(本题5分)已知点为抛物线的焦点,,点为抛物线上一动点,当最小时,点恰好在以,为焦点的双曲线上,则该双曲线的渐近线的斜率的平方为( )
A. B. C. D.
12.(本题5分)已知定义在上的函数的导函数为,满足.当时,.当时,,且,其中是自然对数的底数.则的取值范围为( )
A. B. C. D.
二、填空题(共20分)
13.(本题5分)正方形的边长为2,圆内切于正方形,为圆的一条动直径,点为正方形边界上任一点,则的取值范围是______.
14.(本题5分)在平面上,将两个半圆弧和、两条直线和围成的封闭图形记为,如图中阴影部分.记绕轴旋转一周而成的几何体为,过作的水平截面,所得截面面积为,试利用祖暅原理(祖暅原理:“幂势既同,则积不容异”,意思是:两等高的几何体在同高处被截得的两个截面面积均相等,那么这两个几何体的体积相等)、一个平放的圆柱和一个长方体,得出的体积值为__________.
(本题5分)设△AnBnCn的三边长分别为an,bn,cn,n=1,2,3…,若,,,,则的最大值是________________.
(本题5分)某校高二年级共有10个班级,5位教学教师,每位教师教两个班级,其中姜老师一定教1班,张老师一定教3班,王老师一定教8班,秋老师至少教9班和10班中的一个班,曲老师不教2班和6班,王老师不教5班,则不同的排课方法种数______.
参考答案
1.A
【分析】
根据题意,利用数形结合表示出集合,然后根据新定义中集合中元素的构成,用平面的点表示即可.
【详解】
因为集合,所以集合中有5个元素(即5个点),即图中圆中的整点(包括边界),集合中有个元素(即49个点):即图中正方形中的整点,
集合的元素可看作正方形中的整点(除去四个顶点),即个.
含有个元素.
故选:A.
2.A
【详解】
试题分析:∵在复平面内关于虚轴对称,,∴,∴。故选:A.
3.A
【分析】
首先设函数,由条件确定周期和的范围,再利用对称性求出对称中心和对称轴,求,代入求,利用伸缩变换求,最后解不等式.
【详解】
函数的最大值为2,,
在区间上单调,所以,即,
,即,
,是函数的对称轴,
,是函数的对称中心,
和是函数相邻的对称轴和对称中心,,得,
当时,取到最大值2,,,
当时,,
,根据题意可知,
,
,解得:,.
的解集是.
故选:A.
4.C
【分析】
作于点E,于点M,根据平面向量的定义,结合锐角三角函数的定义、垂径定理、平面向量的几何意义进行求解即可.
【详解】
作图如下:
由题意得:作于点E,于点M,因为,即:所以,又因为,
所以.即.
又因为,所以 ,所以.即 在上的投影为.
.
故选:C.
5.D
【分析】
分别求出每个人去打篮球、打乒乓球的概率,的所有可能取值为0,2,4,利用二项分布的概率公式求出的分布列即可求得的期望值.
【详解】
依题意,这4个人中,每个人去打篮球的概率为,去打乒乓球的概率为,
设“这4个人中恰有人去打篮球”为事件,
则﹐的所有可能取值为0,2,4.
由于与互斥﹐与互斥,故﹐
,
所以的分布列为
2 2 4
随机变量ξ的数学期望.
故选:D.
6.B
【分析】
先用组合数的性质求和得,再逐一验证即可
【详解】
因为,
令,,
令的前项和为,
则
,
对于A:,
则,解得,故A有可能;
对于B:,
则,
因为,
故无正整数解,故B不可能;
对于C:,
则,解得,故C有可能;
对于D:,
则,解得,故D有可能;
故选:B.
7.A
【分析】
令,根据条件可知有两个不同的零点,然后分三种情况,求出k的取值范围.
【详解】
解:令,则,
∵和图象有且仅有两个不同的公共点,∴有两个不同的零点,
又,
当时,在上单调递增,在上单调递减,且,
∴图象的左右两边向下无限延伸,故此时有两个零点,∴满足题意;
当时,只有一个零点,不滿足题意;
当时,,在上单调递增,在上单调递减,在上单调递增,且,
易知只有一个零点,不满足题意;
综上,的取值范围是.
故选:A.
8.C
【分析】
转化:,利用余弦定理:,即得解.
【详解】
如图所示,由题意得,
当且仅当:时,有最大值.
故选:C.
9.A
【分析】
求得点的轨迹是平面内以点为圆心,半径为的圆,可得,进而可得出题中所求角等于直线与直线的夹角,然后过点作平面于点,过点作于点,连接,找出使得最大和最小时的位置,进而可求得所求角的余弦值的取值范围.
【详解】
连接交平面于点,延长线段至点,使得,连接、、,如下图所示:
已知在正方体中,底面,平面,,
又四边形为正方形,所以,,
,平面,平面,,
同理,,平面,
三棱锥的体积为,
,,
可得,
所以,线段的长被平面与平面三等分,且与两平面分别垂直,
而正方体的棱长为,所以,,如下图所示:
其中,不妨设,由题意可,
所以,,可得,
所以,点在平面内以点为圆心,半径为的圆上.
因为,所以,直线与直线的夹角即为直线与直线所成角.
接下来要求出线段与的长,然后在中利用余弦定理求解.
如图,过点作平面于点,过点作于点,连接,
根据题意可知,,且,
所以,,.
如图所示,,当点在处时,最大,当点在处时,最小.
这两种情况下直线与直线夹角的余弦值最大,为;
当点在点处时,为直角,此时余弦值最小为.
综上所述,直线与直线所成角的余弦值的取值范围是.
故选:A.
10.D
【分析】
取中点,中点,中点,根据球的性质,容易知道球心O在线段EF上,设出OE的长度和∠FGQ,算出FQ的长度,利用OC1=OQ,即可判断A,B;
作出过C1,P,Q三点的截面即可判断C;
利用即可求出体积,进而判断D.
【详解】
如图1,取中点,中点,中点,由题意,球心在线段上,设,在中,由余项定理,设,
则,∴,
设外接球半径为R,∵,∴,
∴,∴,∴球的表面积,C错误;
当点Q在的三等分点处,,则,,∴∴球的表面积,A错误;
对B,如图2,取中点,当在上时,连接AF,在平面ADD1A1上过点Q作AF的平行线,与线段,AD分别交于M,N,延长C1P与BC交于R,连接RN交AB于S,此时截面为,B错误;
对D,当点P位于的中点处,三棱锥的体积为定值,D正确.
故选:D.
11.B
【分析】
作出图形,可知与抛物线相切时,取得最小值,求出点的坐标,利用双曲线定义求出2a,结合,可求得,再利用求得结果.
【详解】
由抛物线的对称性,设为抛物线第一象限内点,如图所示:
故点作垂直于抛物线的准线于点B,由抛物线的定义知,易知轴,可得
当取得最大值时,取得最小值,此时与抛物线相切,
设直线方程为:,
联立,整理得,
其中,解得:,由为抛物线第一象限内点,则
则,解得:,此时,即或
所以点的坐标且
由题意知,双曲线的左焦点为,右焦点为
设双曲线的实轴长为2a,则,,
又,则
故渐近线斜率的平方为
故选:B.
12.B
【分析】
根据题意,构造函数和,对于,由题意可得,利用导数分析可得在区间上单调递增,进而有,对其变形可得,同理分析的单调性可得,综合即可得答案.
【详解】
根据题意,设,(),,()
∵,∴,
即,∴
对于,其导数,
∵,,则有在区间上单调递增;
所以,即,变形可得;
对于,其导数,
∵时,,则在区间上单调递减;
则有,即,变形可得,
综合可得:,即的范围为.
故选:B.
13.
【分析】
根据向量关系表示,只需求出的取值范围即可得解.
【详解】
由题可得:,
故答案为:
14.
【分析】
由题目给出的的水平截面的面积,可猜想水平放置的圆柱和长方体的量,然后直接求出圆柱的体积与长方体的体积作和即可.
【详解】
因为几何体的水平截面的截面面积为,该截面的截面面积由两部分组成,一部分为定值,看作是截一个底面积为,高为2的长方体得到的,对于,看作是把一个半径为1,高为的圆柱得到的,如图所示:
这两个几何体和放在一起,根据祖暅原理,每个平行水平面的截面面积相等,故它们体积相等,即的体积为。故填:.
15.
【分析】
根据题干条件得到,进而利用余弦定理及基本不等式求出,从而求出的最大值是.
【详解】
由,得:,
又,所以,,所以,所以
,当且仅当时等号成立,此时三角形为等边三角形,所以的最大值是.
故答案为:.
16.236
【分析】
按照特殊元素优先处理原则,分类讨论秋老师教9班,秋老师教10班的排课方法种数,但这两种重复了秋老师同时教9班和10班的排课方法种数,减去即可得到答案.
【详解】
(1)秋老师教9班,曲老师可在4,5,7,10班中选两班,再分两小类:
①曲老师不教5班,则曲老师可选(种);王老师可选(种);剩余的3个班3个老师全排列安排有(种);按分步相乘计数原理有:(种);
②曲老师教5班,则曲老师可选(种);剩余的4个班4个老师全排列安排有(种);按分步相乘计数原理有:(种).
按分类相加计数原理,秋老师教9班有:(种);
(2)秋老师教10班,同理也有126(种);
(3)秋老师同时教9班和10班,曲老师可在4,5,7班中选两班,再分两小类:
①曲老师不教5班,则曲老师教4班和7班,王老师再从2,6班选一个,可选(种);剩余的2个班2个老师全排列安排有(种);按分步相乘计数原理有:(种);
②曲老师教5班,则曲老师可选(种);剩余的3个班3个老师全排列安排有(种);按分步相乘计数原理有:(种).
按分类相加计数原理,秋老师同时教9班和10班有:(种);
但秋老师同时教9班和10班在(1)和(2)两种分类里都涉及到,所以重复需减去,
故不同的排课方法种数有:(种).
故答案为:236.
同课章节目录
