人教版2021-2022学年数学七年级下册5.2.2平行线的判定同步课堂练习(word版、含解析)
文档属性
| 名称 | 人教版2021-2022学年数学七年级下册5.2.2平行线的判定同步课堂练习(word版、含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 323.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-30 00:00:00 | ||
图片预览


文档简介
2021-2022年初中数学七年级下册同步(人教版)
5.2.2平行线的判定-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在同一平面内,有8条互不重合的直线:,,,…,,若,,,…,依次类推,则和的位置关系是( )
A.平行 B.垂直 C.平行或垂直 D.无法确定
2.如图,直线、都与直线相交,有下列条件:①;②;③;④.其中,能够判断的是( )
A.①②③④ B.①③ C.②③④ D.①②
3.如图,能判定的条件是( )
A. B.
C. D.
4.如图,在下列给出的条件中,不能判定的是( )
A. B. C. D.
5.如图,下列能判定的条件有( )个.
(1);(2);(3);(4).
A.1 B.2 C.3 D.4
6.如图所示,点E在的延长线上,下列条件中能判断的是( )
A. B. C. D.
二、填空题
7.在同一平面内有三条直线l1、l2、l3,若l1⊥l2,l2⊥l3,则l1与l3的位置关系是__.
8.如图所示,在下列条件中,不能判断的有___________.
①. ②. ③. ④.
9.如图所示,若,则_______________,根据是_____________________.
10.如图所示,请你填写一个适当的条件:_____,使AD∥BC.
11.如图,∠EFB=∠GHD=53°,∠IGA=127°,由这些条件,能找到_____对平行线.
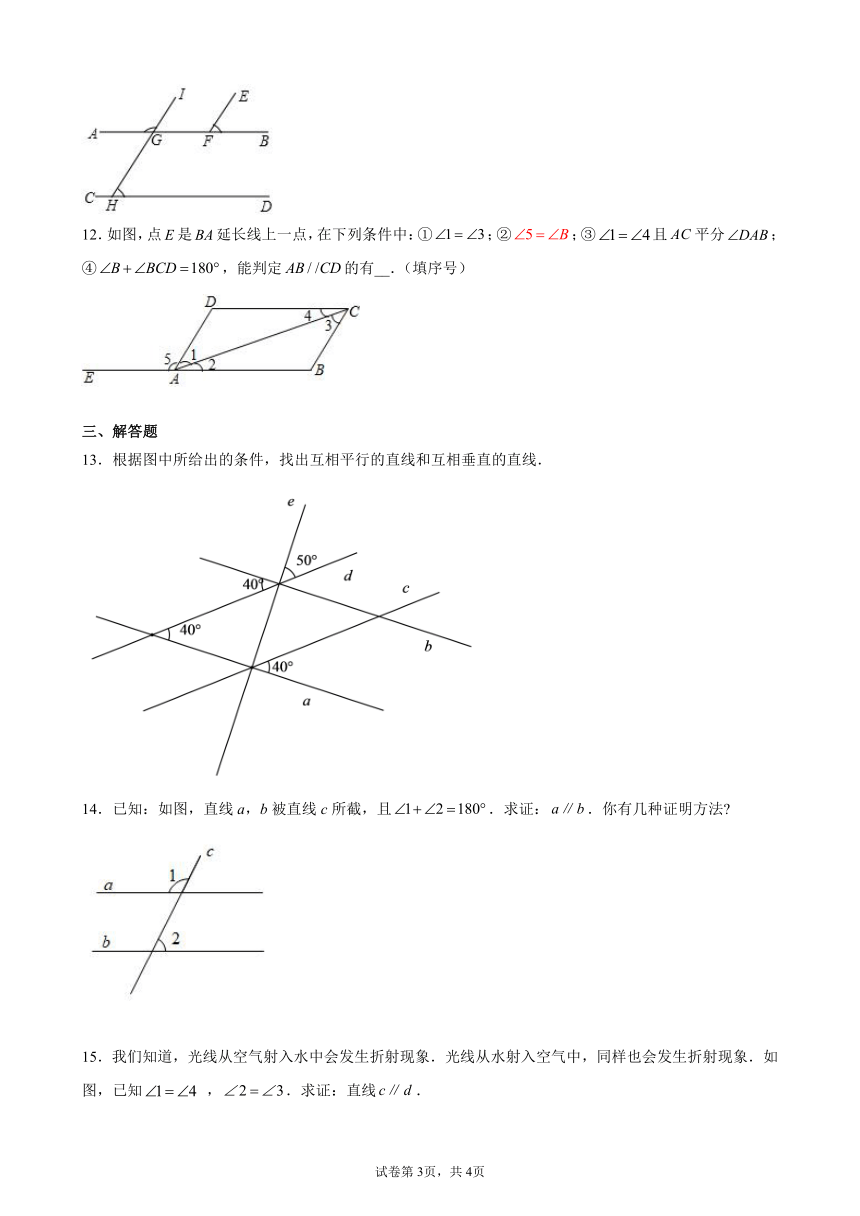
12.如图,点是延长线上一点,在下列条件中:①;②;③且平分;④,能判定的有__.(填序号)
三、解答题
13.根据图中所给出的条件,找出互相平行的直线和互相垂直的直线.
14.已知:如图,直线a,b被直线c所截,且.求证:.你有几种证明方法
15.我们知道,光线从空气射入水中会发生折射现象.光线从水射入空气中,同样也会发生折射现象.如图,已知 ,.求证:直线.
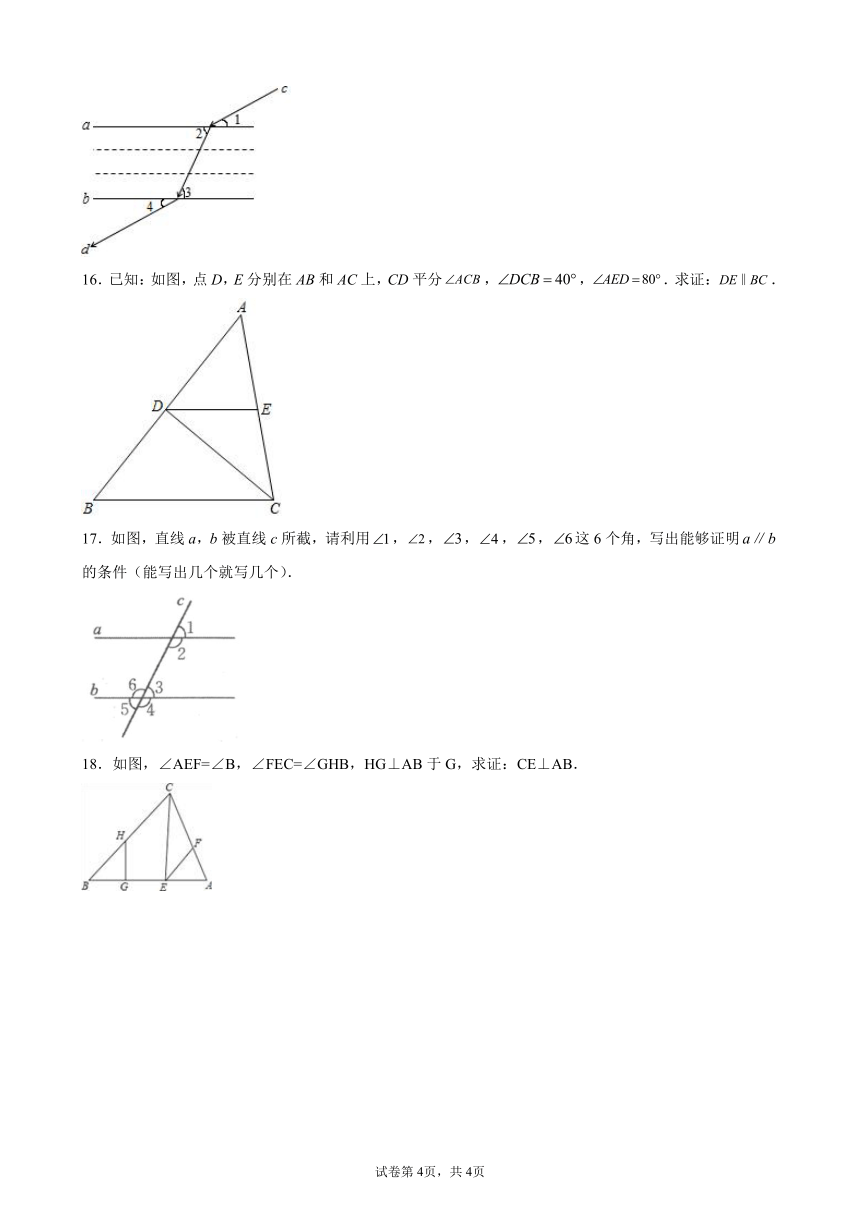
16.已知:如图,点D,E分别在AB和AC上,CD平分,,.求证:.
17.如图,直线a,b被直线c所截,请利用,,,,,这6个角,写出能够证明的条件(能写出几个就写几个).
18.如图,∠AEF=∠B,∠FEC=∠GHB,HG⊥AB于G,求证:CE⊥AB.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【解析】解:如图,图中8条直线满足条件,
由图可知:,,
可推出,
∵,
∴,
∵,
∴,
以此类推:.
故选A.
2.A
【解析】解:①,,故本小题正确;
②,,故本小题正确;
③,,,,故本小题正确;
④,,,,故本小题正确.
答案:A.
3.D
【解析】根据∠B=∠ACB,不能得到EC//AB,故A错误;
根据∠A=∠ECD,不能得到EC//AB故B错误;
根据∠B=∠ACE,不能得到EC//AB,故C错误;
根据∠A=∠ACE,能判定EC//AB,,故D正确;
故选:D.
4.B
【解析】解:A、∵∠B=∠3,∴AB∥EF(同位角相等,两直线平行),不符合题意;
B、∵∠1=∠B,∴BC∥DF(同位角相等,两直线平行),不能证出AB∥EF,符合题意;
C、∵∠1=∠4,∴AB∥EF(内错角相等,两直线平行),不符合题意;
D、∵∠B+∠2=180,∴AB∥EF(同旁内角互补,两直线平行),不符合题意;
故选:B.
5.C
【解析】解:当∠B+∠BCD=180°,AB∥CD,符合题意;
当∠1=∠2时,AD∥BC,不符合题意;
当∠3=∠4时,AB∥CD,符合题意;
当∠B=∠5时,AB∥CD,符合题意.
综上,符合题意的有3个,
故选:C.
6.B
【解析】当时,,故A不符合题意;
当时,,故B符合题意;
当时,,故C不符合题意;
当时,,故D不符合题意;
故答案选B.
7.平行.
【解析】∵l1⊥l2,l2⊥l3,∴l1∥l2.
8.②
【解析】解:①∵,
∴(内错角相等,两直线平行),说法正确,不符合题意;
②∵和既不是同位角,也不是内错角,
∴不能根据判定,说法错误,符合题意;
③∵,,
∴,
∴(同旁内角互补,两直线平行),说法正确,不符合题意;
④∵,
∴(同旁内角互补,两直线平行),说法正确,不符合题意;
故答案为:②.
9.AD BC 同旁内角互补,两直线平行
【解析】解:∵,
∴,
∴(同旁内角互补,两直线平行),
故答案为:AD;BC;同旁内角互补,两直线平行.
10.∠FAD=∠FBC(答案不唯一)
【解析】根据同位角相等,两直线平行,可填∠FAD=∠FBC;
根据内错角相等,两直线平行,可填∠ADB=∠DBC;
根据同旁内角互补,两直线平行,可填∠DAB+∠ABC=180°.
故答案为:∠FAD=∠FBC;或∠ADB=∠DBC;或∠DAB+∠ABC=180°.
11.2
【解析】解:∵∠GHD=53°,
∵∠GHC=127°,
∵∠IGA=127°,
∴∠GHC=∠IGA,∠IGB=53°,
∴AB∥CD,
∵∠EFB=53°,
∴∠IGB=∠EFB,
∴IH∥EF.
故答案为:2.
12.③④
【解析】①中,,(内错角相等,两直线平行),不合题意;
②中,,(同位角相等,两直线平行),不合题意;
③中,且平分,,,故此选项符合题意;
④中,, (同旁内角互补,两直线平行),故此选项符合题意;
答案:③④.
13.,,,.
【解析】解:根据内错角相等可判断a∥b;根据同位角相等可判断c∥d;
∵40°+50°=90°,
∴根据垂直的定义可判断b⊥e,则a⊥e.
14.证明见解析.
【解析】解:①∵∠1+∠2=180°,∠1=∠5,
∴∠5+∠2=180°,
∴a∥b(同旁内角互补,两直线平行);
②∵∠1+∠2=180°,∠1+∠3=180°,
∴∠3=∠2,
∴a∥b(同位角相等,两直线平行);
③∵∠1+∠2=180°,∠1+∠4=180°,
∴∠4=∠2,
∴a∥b(内错角相等,两直线平行).
15.见解析
【解析】证:如图所示,
∵,
∴,
∵,
∴,
即:,
∵是直线被直线所截形成的内错角,
∴直线.
16.证明见解析.
【解析】证明:∵CD平分(已知),
∴(角平分线的定义).
∵(已知),
∴(等量代换).
∴(同位角相等,两直线平行).
17.见解析
【解析】符合要求的条件很多,如下列任何一个条件都符合要求:,,,,,,,
18.证明见解析.
【解析】证明:∵∠AEF=∠B,
∴EF∥BC,
∴∠FEC=∠BCE=∠GHB,
∴GH∥CE,
∴∠CEB=∠BGH,
∵HG⊥AB,
∴∠CEB=∠BGH,
∴CE⊥AB 答案第1页,共2页
答案第1页,共2页
5.2.2平行线的判定-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在同一平面内,有8条互不重合的直线:,,,…,,若,,,…,依次类推,则和的位置关系是( )
A.平行 B.垂直 C.平行或垂直 D.无法确定
2.如图,直线、都与直线相交,有下列条件:①;②;③;④.其中,能够判断的是( )
A.①②③④ B.①③ C.②③④ D.①②
3.如图,能判定的条件是( )
A. B.
C. D.
4.如图,在下列给出的条件中,不能判定的是( )
A. B. C. D.
5.如图,下列能判定的条件有( )个.
(1);(2);(3);(4).
A.1 B.2 C.3 D.4
6.如图所示,点E在的延长线上,下列条件中能判断的是( )
A. B. C. D.
二、填空题
7.在同一平面内有三条直线l1、l2、l3,若l1⊥l2,l2⊥l3,则l1与l3的位置关系是__.
8.如图所示,在下列条件中,不能判断的有___________.
①. ②. ③. ④.
9.如图所示,若,则_______________,根据是_____________________.
10.如图所示,请你填写一个适当的条件:_____,使AD∥BC.
11.如图,∠EFB=∠GHD=53°,∠IGA=127°,由这些条件,能找到_____对平行线.
12.如图,点是延长线上一点,在下列条件中:①;②;③且平分;④,能判定的有__.(填序号)
三、解答题
13.根据图中所给出的条件,找出互相平行的直线和互相垂直的直线.
14.已知:如图,直线a,b被直线c所截,且.求证:.你有几种证明方法
15.我们知道,光线从空气射入水中会发生折射现象.光线从水射入空气中,同样也会发生折射现象.如图,已知 ,.求证:直线.
16.已知:如图,点D,E分别在AB和AC上,CD平分,,.求证:.
17.如图,直线a,b被直线c所截,请利用,,,,,这6个角,写出能够证明的条件(能写出几个就写几个).
18.如图,∠AEF=∠B,∠FEC=∠GHB,HG⊥AB于G,求证:CE⊥AB.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【解析】解:如图,图中8条直线满足条件,
由图可知:,,
可推出,
∵,
∴,
∵,
∴,
以此类推:.
故选A.
2.A
【解析】解:①,,故本小题正确;
②,,故本小题正确;
③,,,,故本小题正确;
④,,,,故本小题正确.
答案:A.
3.D
【解析】根据∠B=∠ACB,不能得到EC//AB,故A错误;
根据∠A=∠ECD,不能得到EC//AB故B错误;
根据∠B=∠ACE,不能得到EC//AB,故C错误;
根据∠A=∠ACE,能判定EC//AB,,故D正确;
故选:D.
4.B
【解析】解:A、∵∠B=∠3,∴AB∥EF(同位角相等,两直线平行),不符合题意;
B、∵∠1=∠B,∴BC∥DF(同位角相等,两直线平行),不能证出AB∥EF,符合题意;
C、∵∠1=∠4,∴AB∥EF(内错角相等,两直线平行),不符合题意;
D、∵∠B+∠2=180,∴AB∥EF(同旁内角互补,两直线平行),不符合题意;
故选:B.
5.C
【解析】解:当∠B+∠BCD=180°,AB∥CD,符合题意;
当∠1=∠2时,AD∥BC,不符合题意;
当∠3=∠4时,AB∥CD,符合题意;
当∠B=∠5时,AB∥CD,符合题意.
综上,符合题意的有3个,
故选:C.
6.B
【解析】当时,,故A不符合题意;
当时,,故B符合题意;
当时,,故C不符合题意;
当时,,故D不符合题意;
故答案选B.
7.平行.
【解析】∵l1⊥l2,l2⊥l3,∴l1∥l2.
8.②
【解析】解:①∵,
∴(内错角相等,两直线平行),说法正确,不符合题意;
②∵和既不是同位角,也不是内错角,
∴不能根据判定,说法错误,符合题意;
③∵,,
∴,
∴(同旁内角互补,两直线平行),说法正确,不符合题意;
④∵,
∴(同旁内角互补,两直线平行),说法正确,不符合题意;
故答案为:②.
9.AD BC 同旁内角互补,两直线平行
【解析】解:∵,
∴,
∴(同旁内角互补,两直线平行),
故答案为:AD;BC;同旁内角互补,两直线平行.
10.∠FAD=∠FBC(答案不唯一)
【解析】根据同位角相等,两直线平行,可填∠FAD=∠FBC;
根据内错角相等,两直线平行,可填∠ADB=∠DBC;
根据同旁内角互补,两直线平行,可填∠DAB+∠ABC=180°.
故答案为:∠FAD=∠FBC;或∠ADB=∠DBC;或∠DAB+∠ABC=180°.
11.2
【解析】解:∵∠GHD=53°,
∵∠GHC=127°,
∵∠IGA=127°,
∴∠GHC=∠IGA,∠IGB=53°,
∴AB∥CD,
∵∠EFB=53°,
∴∠IGB=∠EFB,
∴IH∥EF.
故答案为:2.
12.③④
【解析】①中,,(内错角相等,两直线平行),不合题意;
②中,,(同位角相等,两直线平行),不合题意;
③中,且平分,,,故此选项符合题意;
④中,, (同旁内角互补,两直线平行),故此选项符合题意;
答案:③④.
13.,,,.
【解析】解:根据内错角相等可判断a∥b;根据同位角相等可判断c∥d;
∵40°+50°=90°,
∴根据垂直的定义可判断b⊥e,则a⊥e.
14.证明见解析.
【解析】解:①∵∠1+∠2=180°,∠1=∠5,
∴∠5+∠2=180°,
∴a∥b(同旁内角互补,两直线平行);
②∵∠1+∠2=180°,∠1+∠3=180°,
∴∠3=∠2,
∴a∥b(同位角相等,两直线平行);
③∵∠1+∠2=180°,∠1+∠4=180°,
∴∠4=∠2,
∴a∥b(内错角相等,两直线平行).
15.见解析
【解析】证:如图所示,
∵,
∴,
∵,
∴,
即:,
∵是直线被直线所截形成的内错角,
∴直线.
16.证明见解析.
【解析】证明:∵CD平分(已知),
∴(角平分线的定义).
∵(已知),
∴(等量代换).
∴(同位角相等,两直线平行).
17.见解析
【解析】符合要求的条件很多,如下列任何一个条件都符合要求:,,,,,,,
18.证明见解析.
【解析】证明:∵∠AEF=∠B,
∴EF∥BC,
∴∠FEC=∠BCE=∠GHB,
∴GH∥CE,
∴∠CEB=∠BGH,
∵HG⊥AB,
∴∠CEB=∠BGH,
∴CE⊥AB 答案第1页,共2页
答案第1页,共2页
