2021—2022学年人教版数学七年级下册5.3.1平行线的性质-课堂练习(word版、含解析)
文档属性
| 名称 | 2021—2022学年人教版数学七年级下册5.3.1平行线的性质-课堂练习(word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 406.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-30 20:01:06 | ||
图片预览




文档简介
2021-2022年初中数学七年级下册同步(人教版)
5.3.1平行线的性质-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.和是同旁内角,,那么等于( ).
A. B. C.或 D.大小不定
2.如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的,第二次拐的,第三次拐的,这时的道路恰好和第一次拐弯之前的道路平行,则是( )
A. B. C. D.
3.如图,,则满足的数量关系是( )
A. B.
C. D.
4.如图,则下面结论中正确的是( )
A. B. C. D.
5.如图所示, ,下列结论正确的个数为( ).
①;②﹔③﹔④.
A.1个 B.2个 C.3个 D.4个
6.如图,已知直线、被直线所截,,E是直线右边任意一点(点E不在直线,上),设,.下列各式:①,②,③,④,的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题
7.如图,,且CF平分∠AFE,若,则∠A的度数是__.
8.如图,AB∥CD,AD不平行于BC,AC与BD相交于点O,写出三对面积相等的三角形是___________________.
9.如图,点、分别在、上,,,,则___.
10.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为________.
11.如图,若,则____根据是__;若,则____,根据是__;若,则____,根据是__.
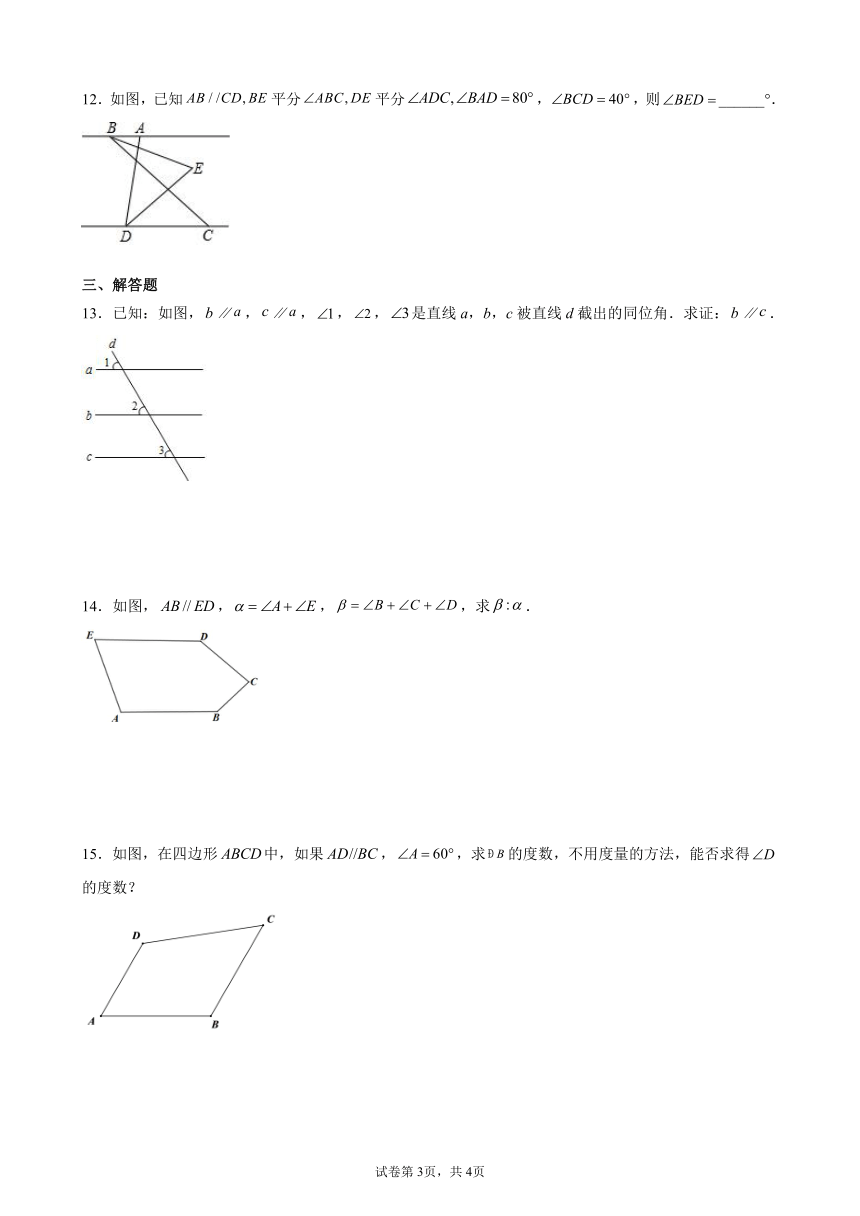
12.如图,已知平分平分,,则______°.
三、解答题
13.已知:如图,∥,∥,,,是直线a,b,c被直线d截出的同位角.求证:∥.
14.如图,,,,求.
15.如图,在四边形中,如果,,求的度数,不用度量的方法,能否求得的度数?
16.如图,点D,E分别在AB和AC上,,,,求的度数.
17.如图,在△ABC中,∠ABC与∠ACB的平分线相交于O.过点O作EF∥BC分别交AB、AC于E、F.若∠BOC=130°,∠ABC:∠ACB=3:2,求∠AEF和∠EFC.
18.(1)已知:如图(a),直线.求证:;
(2)如图(b),如果点C在AB与ED之外,其他条件不变,那么会有什么结果?你还能就本题作出什么新的猜想?
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【解析】解:∵题目并未告诉,∠1和∠2是属于两条平行线被截的同旁内角,
∴∠2的度数大小不能确定,
故选D.
2.D
【解析】解:过点B作直线BD与第一次拐弯的道路平行,如图所示:
∵第三次拐的,这时的道路恰好和第一次拐弯之前的道路平行,
∴直线BD与第三次拐弯的道路也平行,
∵,
∴,,
∵,
∴,
∴;
故选D.
3.A
【解析】解:如图,过点C作CG∥AB,过点D作DH∥EF,
则∠A=∠ACG,∠EDH=180°-∠E,
∵AB∥EF,
∴CG∥DH,
∴∠CDH=∠DCG,
∴∠ACD=∠ACG+∠CDH=∠A+∠CDE-(180°-∠E),
∴∠A-∠ACD +∠CDE +∠E=180°.
即
故选:A.
4.B
【解析】解:,
∴,
故选:B.
5.D
【解析】解:,
,,
,
,,
故选:D.
6.A
【解析】解:(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β-α.
(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.
(3)当点E在CD的下方时,同理可得,∠AEC=α-β.
综上所述,∠AEC的度数可能为β-α,α+β,α-β.
即①α+β,②α-β,③β-α,都成立.
故选A.
7.
【解析】解:∵,,
∴.
又∵CF平分∠AFE,
∴.
∵,
∴.
故答案为:.
8.△ADC和△BDC;△ADO和△BCO;△DAB和△CAB
【解析】根据AB∥CD可得:△ABC和△ABD的面积相等,△ACD和△BCD的面积相等,则△ACD的面积减去△OCD的面积等于△BCD的面积减去△OCD的面积,即△AOD和△BOC的面积相等.
9.60
【解析】,
,
,
,
,
,
.
故答案为:60.
10.2cm或8cm
【解析】当M在b下方时,距离为5-3=2cm;
当M在a、b之间时,距离为5+3=8cm.
故答案为2cm或8cm.
11. 同位角相等,两直线平行 内错角相等,两直线平行 同旁内角互补,两直线平行
【解析】若,则根据是同位角相等,两直线平行;
若,则,根据是内错角相等,两直线平行;
若,则,根据是同旁内角互补,两直线平行.
故答案为:,,同位角相等,两直线平行;,,内错角相等,两直线平行;,,同旁内角互补,两直线平行.
12.60°
【解析】解:∵AB∥CD,
∴∠ABC=∠BCD=40°,∠ADC=∠BAD=80°.
∵BE平分∠ABC,DE平分∠ADC,
∴,
过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,EF∥CD,
∴,
∴,
故答案为:60°.
13.证明见解析.
【解析】证明:∵(已知),
∴(两直线平行,同位角相等).
∵(已知),
∴ (两直线平行,同位角相等).
∴ (等量代换).
∴(同位角相等,两直线平行).
14.2:1
【解析】解:过C点作CF∥AB,
∵AB∥ED,
∴CF∥DE,
∴∠B+∠2=∠D+∠1=180°,
∴β=∠B+∠BCD+∠D=∠B+∠2+∠D+∠1=360°,
∵AB∥DE,
∴∠A+∠E=α=180°,
∴β:α=360°:180°=2:1,
15.,不能求得的度数.
【解析】解:由,,根据“两直线平行,同旁内角互补”
∴,
由于和不平行,
∴不用度量的方法,仅根据平行线的性质,不能求得的度数.
16.
【解析】解:∵,,
∴∠ABC=∠DBE+∠EBC=55°,
∵DE∥BC,
∴∠BDE+∠ABC=180°,
∴∠BDE=180°-∠ABC=125°.
17.∠AEF=60°,∠EFC=140°.
【解析】∵∠ABC: ∠ACB=3:2,
∴设∠ABC=3x, ∠ACB=2x,
∵BO、CO分别平分 ∠ ABC、 ∠ ACB,
∴∠ABO=∠CBO=x,∠ACO=∠BCO=x,
又∵∠BOC=130°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∴130°+x+x=180°,
解得:x=20°,
∴∠ABC=3x=60°, ∠ACB=2x=40°,
∵EF∥BC,
∴∠AEF=∠ABC=60°,
∠EFC+∠ACB=180°,
∴∠EFC=140°.
18.(1)见解析;(2)当点C在AB与ED之外时,,见解析
【解析】解:(1)证明:过点C 作CF∥AB,
∵AB∥ED,
∴AB∥ED∥CF,
∴∠BCF=∠ABC,∠DCF=∠EDC,
∴∠ABC+∠CDE=∠BCD;
(2)结论:∠ABC-∠CDE=∠BCD,
证明:如图:
∵AB∥ED,
∴∠ABC=∠BFD,
在△DFC中,∠BFD=∠BCD+∠CDE,
∴∠ABC=∠BCD+∠CDE,
∴∠ABC-∠CDE=∠BCD.
若点C在直线AB与DE之间,猜想,
∵AB∥ED∥CF,
∴
∴.
答案第1页,共2页
答案第1页,共2页
5.3.1平行线的性质-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.和是同旁内角,,那么等于( ).
A. B. C.或 D.大小不定
2.如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的,第二次拐的,第三次拐的,这时的道路恰好和第一次拐弯之前的道路平行,则是( )
A. B. C. D.
3.如图,,则满足的数量关系是( )
A. B.
C. D.
4.如图,则下面结论中正确的是( )
A. B. C. D.
5.如图所示, ,下列结论正确的个数为( ).
①;②﹔③﹔④.
A.1个 B.2个 C.3个 D.4个
6.如图,已知直线、被直线所截,,E是直线右边任意一点(点E不在直线,上),设,.下列各式:①,②,③,④,的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题
7.如图,,且CF平分∠AFE,若,则∠A的度数是__.
8.如图,AB∥CD,AD不平行于BC,AC与BD相交于点O,写出三对面积相等的三角形是___________________.
9.如图,点、分别在、上,,,,则___.
10.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为________.
11.如图,若,则____根据是__;若,则____,根据是__;若,则____,根据是__.
12.如图,已知平分平分,,则______°.
三、解答题
13.已知:如图,∥,∥,,,是直线a,b,c被直线d截出的同位角.求证:∥.
14.如图,,,,求.
15.如图,在四边形中,如果,,求的度数,不用度量的方法,能否求得的度数?
16.如图,点D,E分别在AB和AC上,,,,求的度数.
17.如图,在△ABC中,∠ABC与∠ACB的平分线相交于O.过点O作EF∥BC分别交AB、AC于E、F.若∠BOC=130°,∠ABC:∠ACB=3:2,求∠AEF和∠EFC.
18.(1)已知:如图(a),直线.求证:;
(2)如图(b),如果点C在AB与ED之外,其他条件不变,那么会有什么结果?你还能就本题作出什么新的猜想?
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【解析】解:∵题目并未告诉,∠1和∠2是属于两条平行线被截的同旁内角,
∴∠2的度数大小不能确定,
故选D.
2.D
【解析】解:过点B作直线BD与第一次拐弯的道路平行,如图所示:
∵第三次拐的,这时的道路恰好和第一次拐弯之前的道路平行,
∴直线BD与第三次拐弯的道路也平行,
∵,
∴,,
∵,
∴,
∴;
故选D.
3.A
【解析】解:如图,过点C作CG∥AB,过点D作DH∥EF,
则∠A=∠ACG,∠EDH=180°-∠E,
∵AB∥EF,
∴CG∥DH,
∴∠CDH=∠DCG,
∴∠ACD=∠ACG+∠CDH=∠A+∠CDE-(180°-∠E),
∴∠A-∠ACD +∠CDE +∠E=180°.
即
故选:A.
4.B
【解析】解:,
∴,
故选:B.
5.D
【解析】解:,
,,
,
,,
故选:D.
6.A
【解析】解:(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β-α.
(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.
(3)当点E在CD的下方时,同理可得,∠AEC=α-β.
综上所述,∠AEC的度数可能为β-α,α+β,α-β.
即①α+β,②α-β,③β-α,都成立.
故选A.
7.
【解析】解:∵,,
∴.
又∵CF平分∠AFE,
∴.
∵,
∴.
故答案为:.
8.△ADC和△BDC;△ADO和△BCO;△DAB和△CAB
【解析】根据AB∥CD可得:△ABC和△ABD的面积相等,△ACD和△BCD的面积相等,则△ACD的面积减去△OCD的面积等于△BCD的面积减去△OCD的面积,即△AOD和△BOC的面积相等.
9.60
【解析】,
,
,
,
,
,
.
故答案为:60.
10.2cm或8cm
【解析】当M在b下方时,距离为5-3=2cm;
当M在a、b之间时,距离为5+3=8cm.
故答案为2cm或8cm.
11. 同位角相等,两直线平行 内错角相等,两直线平行 同旁内角互补,两直线平行
【解析】若,则根据是同位角相等,两直线平行;
若,则,根据是内错角相等,两直线平行;
若,则,根据是同旁内角互补,两直线平行.
故答案为:,,同位角相等,两直线平行;,,内错角相等,两直线平行;,,同旁内角互补,两直线平行.
12.60°
【解析】解:∵AB∥CD,
∴∠ABC=∠BCD=40°,∠ADC=∠BAD=80°.
∵BE平分∠ABC,DE平分∠ADC,
∴,
过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,EF∥CD,
∴,
∴,
故答案为:60°.
13.证明见解析.
【解析】证明:∵(已知),
∴(两直线平行,同位角相等).
∵(已知),
∴ (两直线平行,同位角相等).
∴ (等量代换).
∴(同位角相等,两直线平行).
14.2:1
【解析】解:过C点作CF∥AB,
∵AB∥ED,
∴CF∥DE,
∴∠B+∠2=∠D+∠1=180°,
∴β=∠B+∠BCD+∠D=∠B+∠2+∠D+∠1=360°,
∵AB∥DE,
∴∠A+∠E=α=180°,
∴β:α=360°:180°=2:1,
15.,不能求得的度数.
【解析】解:由,,根据“两直线平行,同旁内角互补”
∴,
由于和不平行,
∴不用度量的方法,仅根据平行线的性质,不能求得的度数.
16.
【解析】解:∵,,
∴∠ABC=∠DBE+∠EBC=55°,
∵DE∥BC,
∴∠BDE+∠ABC=180°,
∴∠BDE=180°-∠ABC=125°.
17.∠AEF=60°,∠EFC=140°.
【解析】∵∠ABC: ∠ACB=3:2,
∴设∠ABC=3x, ∠ACB=2x,
∵BO、CO分别平分 ∠ ABC、 ∠ ACB,
∴∠ABO=∠CBO=x,∠ACO=∠BCO=x,
又∵∠BOC=130°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∴130°+x+x=180°,
解得:x=20°,
∴∠ABC=3x=60°, ∠ACB=2x=40°,
∵EF∥BC,
∴∠AEF=∠ABC=60°,
∠EFC+∠ACB=180°,
∴∠EFC=140°.
18.(1)见解析;(2)当点C在AB与ED之外时,,见解析
【解析】解:(1)证明:过点C 作CF∥AB,
∵AB∥ED,
∴AB∥ED∥CF,
∴∠BCF=∠ABC,∠DCF=∠EDC,
∴∠ABC+∠CDE=∠BCD;
(2)结论:∠ABC-∠CDE=∠BCD,
证明:如图:
∵AB∥ED,
∴∠ABC=∠BFD,
在△DFC中,∠BFD=∠BCD+∠CDE,
∴∠ABC=∠BCD+∠CDE,
∴∠ABC-∠CDE=∠BCD.
若点C在直线AB与DE之间,猜想,
∵AB∥ED∥CF,
∴
∴.
答案第1页,共2页
答案第1页,共2页
