6-2矩形的性质与判定 知识点分类训练 2021-2022学年鲁教版(五四制)八年级数学下册(word版含答案)
文档属性
| 名称 | 6-2矩形的性质与判定 知识点分类训练 2021-2022学年鲁教版(五四制)八年级数学下册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 206.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-30 17:37:57 | ||
图片预览


文档简介
2021-2022学年鲁教版八年级数学下册《6-2矩形的性质与判定》知识点分类训练(附答案)
一.矩形的性质
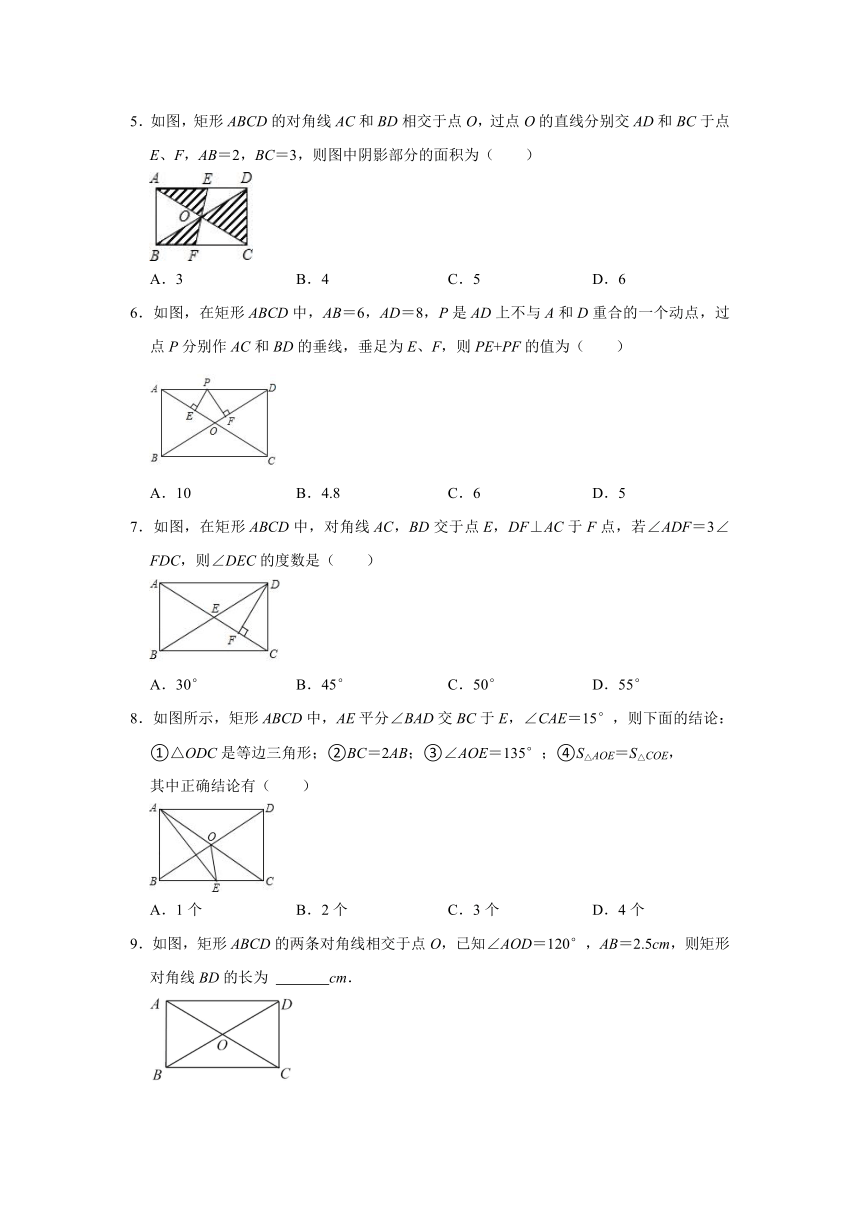
1.如图、在平面直角坐标系xOy中,矩形OABC的顶点A,C的坐标分别是(4,﹣2),(1,2),点B在x轴上,则点B的横坐标是( )
A.4 B.2 C.5 D.4
2.如图,矩形ABCD中,对角线AC,BD交于点O,若∠AOB=60°,BD=8,则DC长为( )
A.4 B.4 C.3 D.5
3.如图,矩形ABCD中,对角线AC,BD相交于点O,若∠OAD=40°,则∠COD=( )
A.20° B.40° C.80° D.100°
4.如图,在矩形ABCD中,有以下结论:
①△AOB是等腰三角形;②S△ABO=S△ADO;③AC=BD;④AC⊥BD;⑤当∠ABD=45°时,矩形ABCD会变成正方形.
正确结论的个数是( )
A.2 B.3 C.4 D.5
5.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为( )
A.3 B.4 C.5 D.6
6.如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E、F,则PE+PF的值为( )
A.10 B.4.8 C.6 D.5
7.如图,在矩形ABCD中,对角线AC,BD交于点E,DF⊥AC于F点,若∠ADF=3∠FDC,则∠DEC的度数是( )
A.30° B.45° C.50° D.55°
8.如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:
①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,
其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
9.如图,矩形ABCD的两条对角线相交于点O,已知∠AOD=120°,AB=2.5cm,则矩形对角线BD的长为 cm.
10.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=6,BC=2.在运动过程中:
(1)Rt△AOB斜边中线的长度是否发生变化 (填“是”或“否”);
(2)点D到点O的最大距离是 .
11.在平面直角坐标系中,一个长方形的三个顶点的坐标分别为(﹣2,﹣1)、(2,3)、(2,﹣1),则其第四个顶点的坐标为 .
12.如图,E是矩形ABCD的边AD上一点,BE=ED,P是对角线BD上任意一点,PF⊥BE,PG⊥AD,垂足分别为F和G,则PF+PG一定与图中哪条线段的长度相等: .
13.如图,在矩形ABCD中,AB=6,对角线AC、BD相交于点O,AE垂直平分BO于点E,则AD的长为 .
14.矩形的两条对角线的夹角是60°,矩形短边长为3,那么矩形对角线的长为 .
15.如图,矩形ABCD中,AB=3,两条对角线AC、BD所夹的钝角为120°,则对角线BD的长为 .
二.矩形的判定
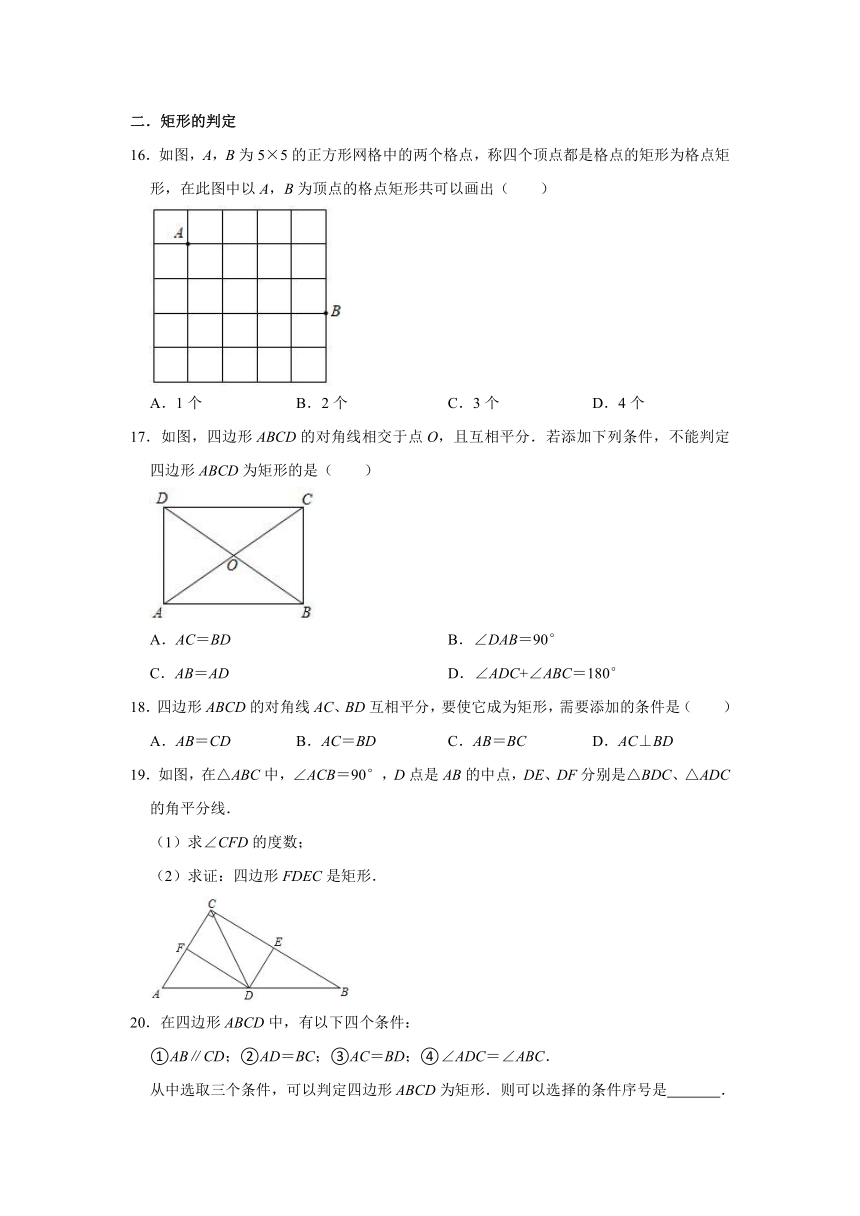
16.如图,A,B为5×5的正方形网格中的两个格点,称四个顶点都是格点的矩形为格点矩形,在此图中以A,B为顶点的格点矩形共可以画出( )
A.1个 B.2个 C.3个 D.4个
17.如图,四边形ABCD的对角线相交于点O,且互相平分.若添加下列条件,不能判定四边形ABCD为矩形的是( )
A.AC=BD B.∠DAB=90°
C.AB=AD D.∠ADC+∠ABC=180°
18.四边形ABCD的对角线AC、BD互相平分,要使它成为矩形,需要添加的条件是( )
A.AB=CD B.AC=BD C.AB=BC D.AC⊥BD
19.如图,在△ABC中,∠ACB=90°,D点是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.
(1)求∠CFD的度数;
(2)求证:四边形FDEC是矩形.
20.在四边形ABCD中,有以下四个条件:
①AB∥CD;②AD=BC;③AC=BD;④∠ADC=∠ABC.
从中选取三个条件,可以判定四边形ABCD为矩形.则可以选择的条件序号是 .
21.如图,在△ABC中,BD是AC的垂直平分线.过点D作AB的平行线交BC于点F,过点B作AC的平行线,两平行线相交于点E,连接CE.求证:四边形BECD是矩形.
三.矩形的判定与性质
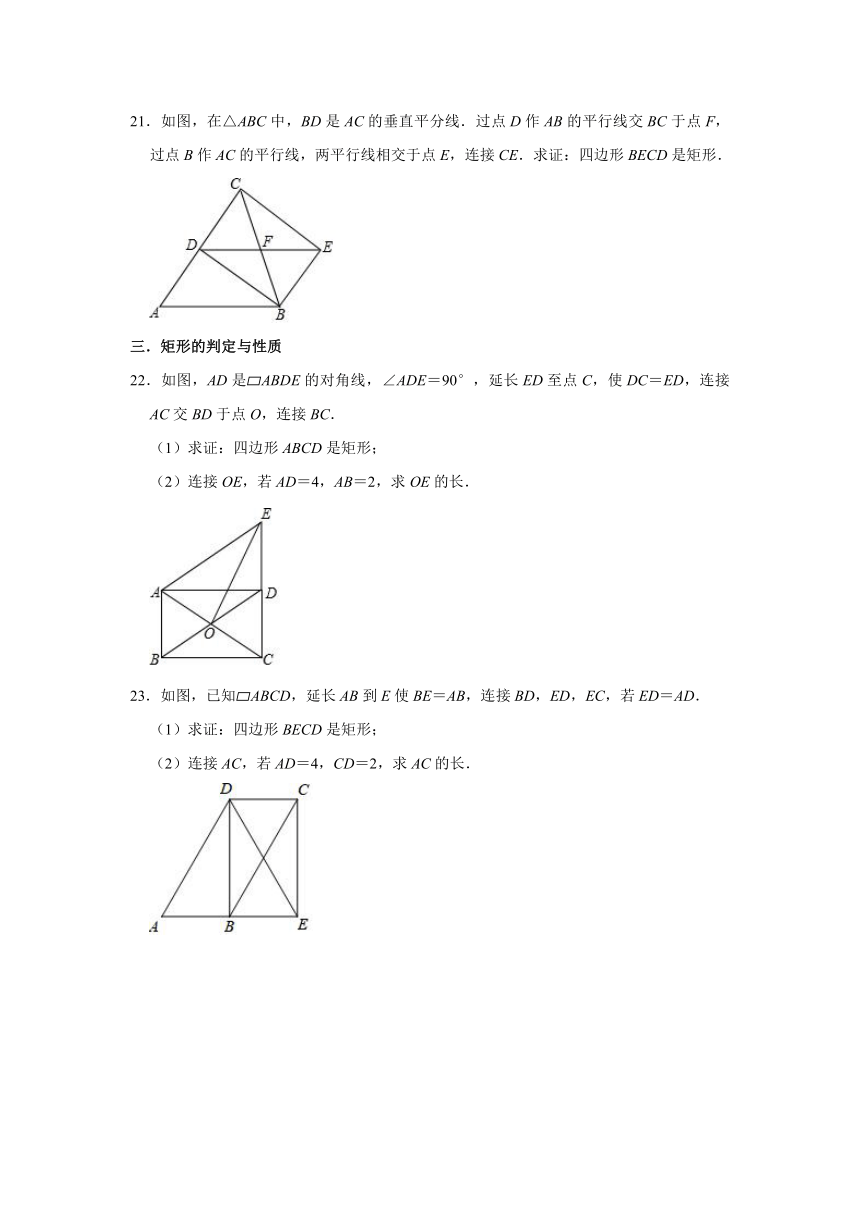
22.如图,AD是 ABDE的对角线,∠ADE=90°,延长ED至点C,使DC=ED,连接AC交BD于点O,连接BC.
(1)求证:四边形ABCD是矩形;
(2)连接OE,若AD=4,AB=2,求OE的长.
23.如图,已知 ABCD,延长AB到E使BE=AB,连接BD,ED,EC,若ED=AD.
(1)求证:四边形BECD是矩形;
(2)连接AC,若AD=4,CD=2,求AC的长.
参考答案
一.矩形的性质
1.解:连接AC,
∵点A(4,﹣2),点C(1,2),
∴AC==5,
∵四边形ABCO是矩形,
∴OB=AC=5,
∴点B的横坐标为5,
故选:C.
2.解:由矩形对角线相等且互相平分可得AO=BO==4,
即△OAB为等腰三角形,
又∠AOB=60°,
∴△OAB为等边三角形.
故AB=BO=4,
∴DC=AB=4.
故选:B.
3.解:∵矩形ABCD中,对角线AC,BD相交于点O,
∴OD=OB=OA=OC,
∵∠OAD=40°,
∴∠ODA=∠OAD=40°,
∴∠COD=∠ODA+∠OAD=40°+40°=80°,
故选:C.
4.解:∵四边形ABCD是矩形,
∴AO=BO=DO=CO,AC=BD,故①③正确;
∵BO=DO,
∴S△ABO=S△ADO,故②正确;
当∠ABD=45°时,
则∠AOD=90°,
∴AC⊥BD,
∴矩形ABCD变成正方形,故⑤正确,
而④不一定正确,矩形的对角线只是相等,
∴正确结论的个数是4个.
故选:C.
5.解:∵矩形ABCD的对角线AC和BD相交于点O,
∴四边形ABFE里面的空白三角形的面积和四边形EDCF中阴影三角形的面积相等.
∴求阴影部分的面积可看成求四边形ABFE的面积.
∴阴影部分的面积为:(2×3)÷2=3.
故选:A.
6.解:如图,连接OP,
∵AB=6,AD=8,
∴BD===10,
∵四边形ABCD是矩形,
∴OA=OD=×10=5,
∵S△AOD=S△AOP+S△DOP,
∴××6×8=×5 PE+×5 PF,
解得PE+PF=4.8.
故选:B.
7.解:设∠ADF=3x°,∠FDC=x°,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴x+3x=90,
x=22.5°,
即∠FDC=x°=22.5°,
∵DF⊥AC,
∴∠DFC=90°,
∴∠DCE=90°﹣22.5°=67.5°,
∵四边形ABCD是矩形,
∴AC=2EC,BD=2ED,AC=BD,
∴ED=EC,
∴∠BDC=∠DCE=67.5°,
∴∠BDF=∠BDC﹣∠CDF=67.5°﹣22.5°=45°,
∴∠DEC=90°﹣45°=45°
故选:B.
8.解:∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OC,OD=OB,AC=BD,
∴OA=OD=OC=OB,
∵AE平分∠BAD,
∴∠DAE=45°,
∵∠CAE=15°,
∴∠DAC=30°,
∵OA=OD,
∴∠ODA=∠DAC=30°,
∴∠DOC=60°,
∵OD=OC,
∴△ODC是等边三角形,∴①正确;
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°
∴∠DAC=∠ACB=30°,
∴AC=2AB,
∵AC>BC,
∴2AB>BC,∴②错误;
∵AD∥BC,
∴∠DBC=∠ADB=30°,
∵AE平分∠DAB,∠DAB=90°,
∴∠DAE=∠BAE=45°,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠AEB=∠BAE,
∴AB=BE,
∵四边形ABCD是矩形,
∴∠DOC=60°,DC=AB,
∵△DOC是等边三角形,
∴DC=OD,
∴BE=BO,
∴∠BOE=∠BEO=(180°﹣∠OBE)=75°,
∵∠AOB=∠DOC=60°,
∴∠AOE=60°+75°=135°,∴③正确;
∵OA=OC,
∴根据等底等高的三角形面积相等得出S△AOE=S△COE,∴④正确;
故选:C.
9.解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,BO=DO=BD,∠BAD=90°,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,∠ADB=30°,
∴AC=BD=2AB=5(cm).
故答案为:5.
10.解:(1)如图,设斜边中点为Q,在运动过程中,斜边中线OQ==3.
∵AB长度不变,故OQ不变,
故答案为:否;
(2)在矩形的运动过程当中,有DQ+OQ≥OD,
当D、Q、O三点共线时,则有DQ+OQ=OD,此时,OD取得最大值,如图所示,
∵Q为AB中点,
∴AQ==3,
又AD=BC=2,
∴DQ==,
∴OD=DQ+OQ=.
故答案为:.
11.解:如图,A(﹣2,﹣1),B(2,﹣1),C(2,3),
∵四边形ABCD为长方形,
∴D(﹣2,3).
故答案为:(﹣2,3).
12.证明:连接PE,如图
∵BE=ED,PF⊥BE,PG⊥AD,
∴S△BDE=S△BEP+S△DEP
=
=,
又∵四边形ABCD是矩形,
∴BA⊥AD,AB=CD,
∴S△BED=,
∴,
∴PF+PG=AB=CD.
故答案为:AB或CD.
13.解:∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵AE垂直平分OB,
∴AB=AO,
∴OA=AB=OB=6,
∴BD=2OB=12,
∴AD==6,
故答案为:6.
14.解:如图,∵四边形ABCD是矩形,
∴OA=AC,OB=BD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=3,
∴AC=2OA=6.
即矩形对角线的长为6.
故答案为:6.
15.解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,OD=OB=BD,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB=3,
∵OB=BD,
∴BD=6.
故答案为:6.
二.矩形的判定
16.解:如图所示:
以AB为对角线的格点矩形有3个,
以AB为边的格点矩形有1个,
∴以A,B为顶点的格点矩形共可以画出4个,
故选:D.
17.解:∵四边形ABCD的对角线相交于点O,且互相平分,
∴四边形ABCD是平行四边形,
若AC=BD,则四边形ABCD是矩形,
故选项A不符合题意;
若∠DAB=90°,则四边形ABCD是矩形,
故选项B不符合题意;
若AB=AD,则四边形ABCD是菱形,
故选项C符合题意;
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,
若∠ADC+∠ABC=180°,
∴∠ADC=∠ABC=90°,
则四边形ABCD是矩形,
故选项D不符合题意;
故选:C.
18.解:需要添加的条件是AC=BD;理由如下:
∵四边形ABCD的对角线AC、BD互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形);
故选:B.
19.解:(1)∵∠ACB=90°,D是AB的中点,
∴AD=CD,
∵DF是∠ADC的角平分线,
∴DF⊥AC.
∴∠CFD=90°;
(2)证明:如图,
∵∠ACB=90°,D是AB的中点,
∴BD=CD,
∵DE是∠BDC的角平分线,
∴DE⊥BC.
∴∠DEC=90°,
∵∠CFD=90°,
∵∠ACB=90°,
∴四边形DECF是矩形.
20.解:当具备①③④这三个条件,能得到四边形ABCD是矩形.理由如下:
∵AB∥CD,
∴∠BAC=∠DCA,
∵∠ABC=∠ADC,AC=CA,
∴△ABC≌△CDA(AAS),
∴∠ACB=∠DCA,
∴AD∥BC,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD是矩形;
故答案为:①③④.
21.证明:∵BD是AC的垂直平分线
∴AD=DC,BD⊥CA,
∴∠BDC=90°,
∵由题意知:AB∥DE,AD∥BE
∴四边形ABED是平行四边形,
∴AD=BE,
∴DC=BE,
又AC∥BE
即DC∥BE
∴四边形BECD是平行四边形,
∴四边形BECD是矩形.
三.矩形的判定与性质
22.(1)证明:∵四边形ABDE是平行四边形,
∴AB∥DE,AB=ED,
∵DC=ED,
∴DC=AB,DC∥AB,
∴四边形ABCD是平行四边形,
∵DE⊥AD,
∴∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:过O作OF⊥CD于F,
∵四边形ABCD是矩形,AD=4,AB=2
∴DE=CD=AB=2,AD=BC=4,AC=BD,AO=OC,BO=DO,
∴OD=OC,
∵OF⊥CD,
∴DF=CF=CD==1,
∴OF=BC==2,EF=DE+DF=2+1=3,
∴OE===.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵BE=AB,
∴BE=CD,
∴四边形BECD是平行四边形,
∵AD=BC,AD=DE,
∴BC=DE,
∴ BECD是矩形;
(2)解:∵CD=2,
∴AB=BE=2.
∵AD=4,∠ABD=90°,
∴BD==2
∴CE=2
∴AC==2.
一.矩形的性质
1.如图、在平面直角坐标系xOy中,矩形OABC的顶点A,C的坐标分别是(4,﹣2),(1,2),点B在x轴上,则点B的横坐标是( )
A.4 B.2 C.5 D.4
2.如图,矩形ABCD中,对角线AC,BD交于点O,若∠AOB=60°,BD=8,则DC长为( )
A.4 B.4 C.3 D.5
3.如图,矩形ABCD中,对角线AC,BD相交于点O,若∠OAD=40°,则∠COD=( )
A.20° B.40° C.80° D.100°
4.如图,在矩形ABCD中,有以下结论:
①△AOB是等腰三角形;②S△ABO=S△ADO;③AC=BD;④AC⊥BD;⑤当∠ABD=45°时,矩形ABCD会变成正方形.
正确结论的个数是( )
A.2 B.3 C.4 D.5
5.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为( )
A.3 B.4 C.5 D.6
6.如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E、F,则PE+PF的值为( )
A.10 B.4.8 C.6 D.5
7.如图,在矩形ABCD中,对角线AC,BD交于点E,DF⊥AC于F点,若∠ADF=3∠FDC,则∠DEC的度数是( )
A.30° B.45° C.50° D.55°
8.如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:
①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,
其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
9.如图,矩形ABCD的两条对角线相交于点O,已知∠AOD=120°,AB=2.5cm,则矩形对角线BD的长为 cm.
10.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=6,BC=2.在运动过程中:
(1)Rt△AOB斜边中线的长度是否发生变化 (填“是”或“否”);
(2)点D到点O的最大距离是 .
11.在平面直角坐标系中,一个长方形的三个顶点的坐标分别为(﹣2,﹣1)、(2,3)、(2,﹣1),则其第四个顶点的坐标为 .
12.如图,E是矩形ABCD的边AD上一点,BE=ED,P是对角线BD上任意一点,PF⊥BE,PG⊥AD,垂足分别为F和G,则PF+PG一定与图中哪条线段的长度相等: .
13.如图,在矩形ABCD中,AB=6,对角线AC、BD相交于点O,AE垂直平分BO于点E,则AD的长为 .
14.矩形的两条对角线的夹角是60°,矩形短边长为3,那么矩形对角线的长为 .
15.如图,矩形ABCD中,AB=3,两条对角线AC、BD所夹的钝角为120°,则对角线BD的长为 .
二.矩形的判定
16.如图,A,B为5×5的正方形网格中的两个格点,称四个顶点都是格点的矩形为格点矩形,在此图中以A,B为顶点的格点矩形共可以画出( )
A.1个 B.2个 C.3个 D.4个
17.如图,四边形ABCD的对角线相交于点O,且互相平分.若添加下列条件,不能判定四边形ABCD为矩形的是( )
A.AC=BD B.∠DAB=90°
C.AB=AD D.∠ADC+∠ABC=180°
18.四边形ABCD的对角线AC、BD互相平分,要使它成为矩形,需要添加的条件是( )
A.AB=CD B.AC=BD C.AB=BC D.AC⊥BD
19.如图,在△ABC中,∠ACB=90°,D点是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.
(1)求∠CFD的度数;
(2)求证:四边形FDEC是矩形.
20.在四边形ABCD中,有以下四个条件:
①AB∥CD;②AD=BC;③AC=BD;④∠ADC=∠ABC.
从中选取三个条件,可以判定四边形ABCD为矩形.则可以选择的条件序号是 .
21.如图,在△ABC中,BD是AC的垂直平分线.过点D作AB的平行线交BC于点F,过点B作AC的平行线,两平行线相交于点E,连接CE.求证:四边形BECD是矩形.
三.矩形的判定与性质
22.如图,AD是 ABDE的对角线,∠ADE=90°,延长ED至点C,使DC=ED,连接AC交BD于点O,连接BC.
(1)求证:四边形ABCD是矩形;
(2)连接OE,若AD=4,AB=2,求OE的长.
23.如图,已知 ABCD,延长AB到E使BE=AB,连接BD,ED,EC,若ED=AD.
(1)求证:四边形BECD是矩形;
(2)连接AC,若AD=4,CD=2,求AC的长.
参考答案
一.矩形的性质
1.解:连接AC,
∵点A(4,﹣2),点C(1,2),
∴AC==5,
∵四边形ABCO是矩形,
∴OB=AC=5,
∴点B的横坐标为5,
故选:C.
2.解:由矩形对角线相等且互相平分可得AO=BO==4,
即△OAB为等腰三角形,
又∠AOB=60°,
∴△OAB为等边三角形.
故AB=BO=4,
∴DC=AB=4.
故选:B.
3.解:∵矩形ABCD中,对角线AC,BD相交于点O,
∴OD=OB=OA=OC,
∵∠OAD=40°,
∴∠ODA=∠OAD=40°,
∴∠COD=∠ODA+∠OAD=40°+40°=80°,
故选:C.
4.解:∵四边形ABCD是矩形,
∴AO=BO=DO=CO,AC=BD,故①③正确;
∵BO=DO,
∴S△ABO=S△ADO,故②正确;
当∠ABD=45°时,
则∠AOD=90°,
∴AC⊥BD,
∴矩形ABCD变成正方形,故⑤正确,
而④不一定正确,矩形的对角线只是相等,
∴正确结论的个数是4个.
故选:C.
5.解:∵矩形ABCD的对角线AC和BD相交于点O,
∴四边形ABFE里面的空白三角形的面积和四边形EDCF中阴影三角形的面积相等.
∴求阴影部分的面积可看成求四边形ABFE的面积.
∴阴影部分的面积为:(2×3)÷2=3.
故选:A.
6.解:如图,连接OP,
∵AB=6,AD=8,
∴BD===10,
∵四边形ABCD是矩形,
∴OA=OD=×10=5,
∵S△AOD=S△AOP+S△DOP,
∴××6×8=×5 PE+×5 PF,
解得PE+PF=4.8.
故选:B.
7.解:设∠ADF=3x°,∠FDC=x°,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴x+3x=90,
x=22.5°,
即∠FDC=x°=22.5°,
∵DF⊥AC,
∴∠DFC=90°,
∴∠DCE=90°﹣22.5°=67.5°,
∵四边形ABCD是矩形,
∴AC=2EC,BD=2ED,AC=BD,
∴ED=EC,
∴∠BDC=∠DCE=67.5°,
∴∠BDF=∠BDC﹣∠CDF=67.5°﹣22.5°=45°,
∴∠DEC=90°﹣45°=45°
故选:B.
8.解:∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OC,OD=OB,AC=BD,
∴OA=OD=OC=OB,
∵AE平分∠BAD,
∴∠DAE=45°,
∵∠CAE=15°,
∴∠DAC=30°,
∵OA=OD,
∴∠ODA=∠DAC=30°,
∴∠DOC=60°,
∵OD=OC,
∴△ODC是等边三角形,∴①正确;
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°
∴∠DAC=∠ACB=30°,
∴AC=2AB,
∵AC>BC,
∴2AB>BC,∴②错误;
∵AD∥BC,
∴∠DBC=∠ADB=30°,
∵AE平分∠DAB,∠DAB=90°,
∴∠DAE=∠BAE=45°,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠AEB=∠BAE,
∴AB=BE,
∵四边形ABCD是矩形,
∴∠DOC=60°,DC=AB,
∵△DOC是等边三角形,
∴DC=OD,
∴BE=BO,
∴∠BOE=∠BEO=(180°﹣∠OBE)=75°,
∵∠AOB=∠DOC=60°,
∴∠AOE=60°+75°=135°,∴③正确;
∵OA=OC,
∴根据等底等高的三角形面积相等得出S△AOE=S△COE,∴④正确;
故选:C.
9.解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,BO=DO=BD,∠BAD=90°,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,∠ADB=30°,
∴AC=BD=2AB=5(cm).
故答案为:5.
10.解:(1)如图,设斜边中点为Q,在运动过程中,斜边中线OQ==3.
∵AB长度不变,故OQ不变,
故答案为:否;
(2)在矩形的运动过程当中,有DQ+OQ≥OD,
当D、Q、O三点共线时,则有DQ+OQ=OD,此时,OD取得最大值,如图所示,
∵Q为AB中点,
∴AQ==3,
又AD=BC=2,
∴DQ==,
∴OD=DQ+OQ=.
故答案为:.
11.解:如图,A(﹣2,﹣1),B(2,﹣1),C(2,3),
∵四边形ABCD为长方形,
∴D(﹣2,3).
故答案为:(﹣2,3).
12.证明:连接PE,如图
∵BE=ED,PF⊥BE,PG⊥AD,
∴S△BDE=S△BEP+S△DEP
=
=,
又∵四边形ABCD是矩形,
∴BA⊥AD,AB=CD,
∴S△BED=,
∴,
∴PF+PG=AB=CD.
故答案为:AB或CD.
13.解:∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵AE垂直平分OB,
∴AB=AO,
∴OA=AB=OB=6,
∴BD=2OB=12,
∴AD==6,
故答案为:6.
14.解:如图,∵四边形ABCD是矩形,
∴OA=AC,OB=BD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=3,
∴AC=2OA=6.
即矩形对角线的长为6.
故答案为:6.
15.解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,OD=OB=BD,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB=3,
∵OB=BD,
∴BD=6.
故答案为:6.
二.矩形的判定
16.解:如图所示:
以AB为对角线的格点矩形有3个,
以AB为边的格点矩形有1个,
∴以A,B为顶点的格点矩形共可以画出4个,
故选:D.
17.解:∵四边形ABCD的对角线相交于点O,且互相平分,
∴四边形ABCD是平行四边形,
若AC=BD,则四边形ABCD是矩形,
故选项A不符合题意;
若∠DAB=90°,则四边形ABCD是矩形,
故选项B不符合题意;
若AB=AD,则四边形ABCD是菱形,
故选项C符合题意;
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,
若∠ADC+∠ABC=180°,
∴∠ADC=∠ABC=90°,
则四边形ABCD是矩形,
故选项D不符合题意;
故选:C.
18.解:需要添加的条件是AC=BD;理由如下:
∵四边形ABCD的对角线AC、BD互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形);
故选:B.
19.解:(1)∵∠ACB=90°,D是AB的中点,
∴AD=CD,
∵DF是∠ADC的角平分线,
∴DF⊥AC.
∴∠CFD=90°;
(2)证明:如图,
∵∠ACB=90°,D是AB的中点,
∴BD=CD,
∵DE是∠BDC的角平分线,
∴DE⊥BC.
∴∠DEC=90°,
∵∠CFD=90°,
∵∠ACB=90°,
∴四边形DECF是矩形.
20.解:当具备①③④这三个条件,能得到四边形ABCD是矩形.理由如下:
∵AB∥CD,
∴∠BAC=∠DCA,
∵∠ABC=∠ADC,AC=CA,
∴△ABC≌△CDA(AAS),
∴∠ACB=∠DCA,
∴AD∥BC,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD是矩形;
故答案为:①③④.
21.证明:∵BD是AC的垂直平分线
∴AD=DC,BD⊥CA,
∴∠BDC=90°,
∵由题意知:AB∥DE,AD∥BE
∴四边形ABED是平行四边形,
∴AD=BE,
∴DC=BE,
又AC∥BE
即DC∥BE
∴四边形BECD是平行四边形,
∴四边形BECD是矩形.
三.矩形的判定与性质
22.(1)证明:∵四边形ABDE是平行四边形,
∴AB∥DE,AB=ED,
∵DC=ED,
∴DC=AB,DC∥AB,
∴四边形ABCD是平行四边形,
∵DE⊥AD,
∴∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:过O作OF⊥CD于F,
∵四边形ABCD是矩形,AD=4,AB=2
∴DE=CD=AB=2,AD=BC=4,AC=BD,AO=OC,BO=DO,
∴OD=OC,
∵OF⊥CD,
∴DF=CF=CD==1,
∴OF=BC==2,EF=DE+DF=2+1=3,
∴OE===.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵BE=AB,
∴BE=CD,
∴四边形BECD是平行四边形,
∵AD=BC,AD=DE,
∴BC=DE,
∴ BECD是矩形;
(2)解:∵CD=2,
∴AB=BE=2.
∵AD=4,∠ABD=90°,
∴BD==2
∴CE=2
∴AC==2.
