2021-2022学年人教版九年级数学下册26.1.2 反比例函数的图象和性质 同步练习 (word版、含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册26.1.2 反比例函数的图象和性质 同步练习 (word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 295.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-30 20:07:57 | ||
图片预览

文档简介
26.1.2 反比例函数的图象和性质
一、选择题
1.反比例函数y=的图象在 ( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
2.如图,在同一平面直角坐标系中,反比例函数与一次函数y=kx 1(k为常数,且k≠0)的图象可能是( )
A.B.C. D.
3.如图,正比例函数的图象与反比例函数的图象交于,两点,,两边分别交轴,轴于点,,四边形的面积为,轴于点.有下列结论:①;②三角形的面积为;③线段的长为;④不等式的解集是或.其中正确结论的个数是( ).
A. B. C. D.
4.某数学小组在研究了函数y1=x与y2=性质的基础上,进一步探究函数y=y1+y2的性质,经过讨论得到以下几个结论:①函数y=y1+y2的图象与直线y=3没有交点;②函数y=y1+y2的图象与直线y=a只有一个交点,则a=±4;③点(a,b)在函数y=y1+y2的图象上,则点(-a,-b)也在函数y=y1+y2的图象上.以上结论正确的是( )
A.①② B.①②③ C.②③ D.①③
5.下列给出的函数中,其图象是中心对称图形的是 ( )
①y=x; ②y=x2; ③y=.
A.①② B.②③ C.①③ D.都不是
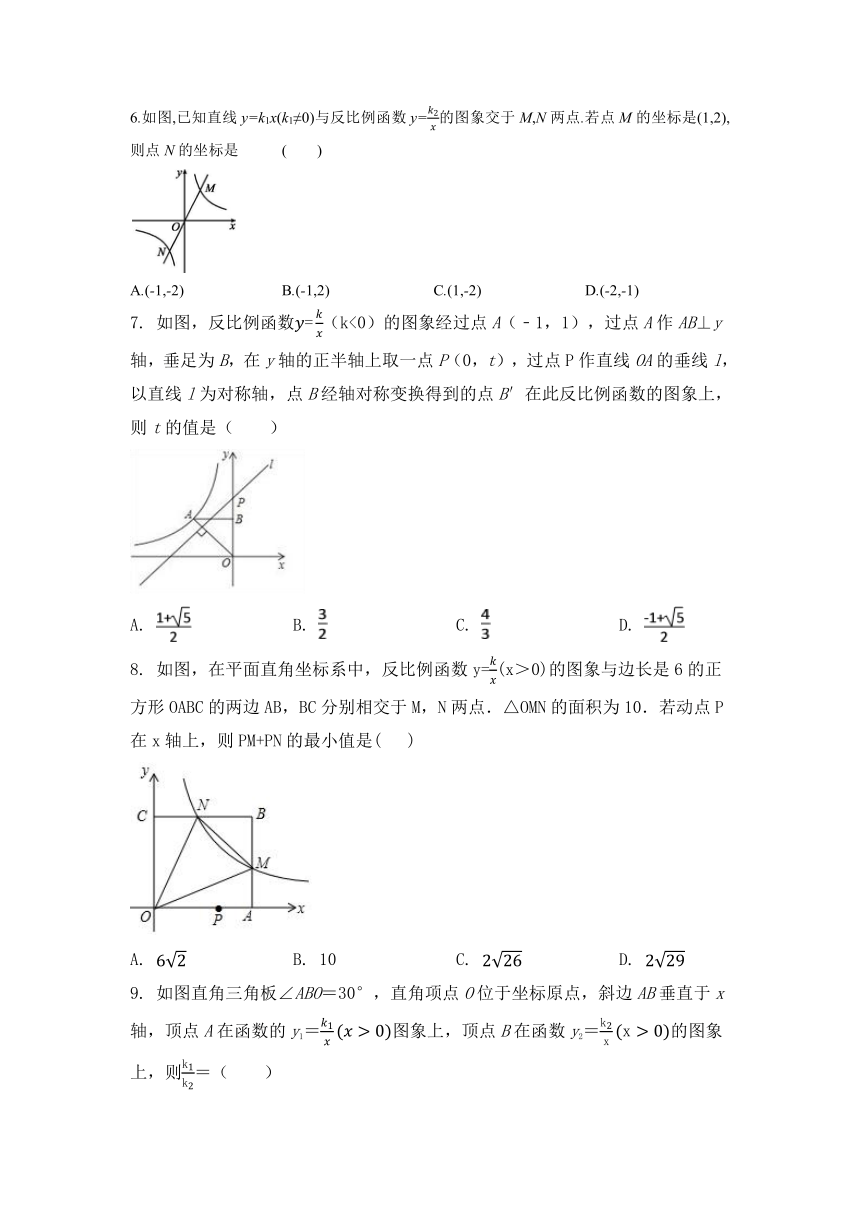
6.如图,已知直线y=k1x(k1≠0)与反比例函数y=的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是 ( )
A.(-1,-2) B.(-1,2) C.(1,-2) D.(-2,-1)
7. 如图,反比例函数(k<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A. B. C. D.
8. 如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A. B. 10 C. D.
9. 如图直角三角板∠ABO=30°,直角项点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数的y1=图象上,顶点B在函数y2=的图象上,则=( )
A. B. C. D.
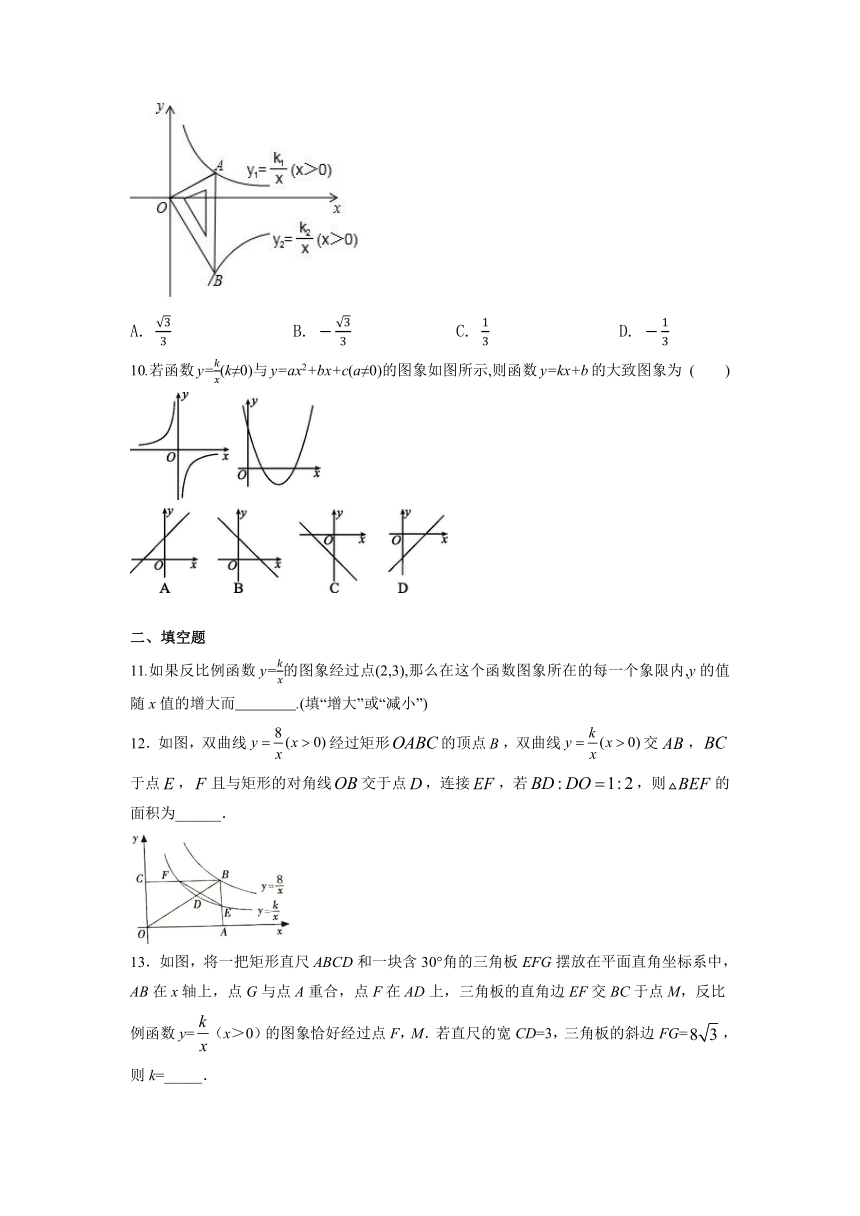
10.若函数y=(k≠0)与y=ax2+bx+c(a≠0)的图象如图所示,则函数y=kx+b的大致图象为 ( )
二、填空题
11.如果反比例函数y=的图象经过点(2,3),那么在这个函数图象所在的每一个象限内,y的值随x值的增大而 .(填“增大”或“减小”)
12.如图,双曲线经过矩形的顶点,双曲线交,于点,且与矩形的对角线交于点,连接,若,则的面积为______.
13.如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数y=(x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=,则k=_____.
14.如图,函数,,,的图象围成阴影部分的面积是___________.
15.如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y=的解析式为_____.
三、解答题
16作出反比例函数 的图象,并结合图象回答:
(1) 当 时, 的值;
(2) 当 时, 的取值范围;
(3) 当 时, 的取值范围.
17已知反比例函数 的图象的一支位于第一象限.
(1) 判断该函数图象的另一支所在的象限,并求 的取值范围;
(2) 如图, 为坐标原点,点 在该反比例函数位于第一象限的图象上,点 与点 关于 轴对称,若 的面积为 ,求 的值.
18如图,在平面直角坐标系中,菱形 的顶点 与原点 重合,点 在 轴的正半轴上,点 在函数 的图象上,点 的坐标为 .
(1) 求 的值;
(2) 若将菱形 沿 轴正方向平移,当菱形的顶点 落在函数 的图象上时,求菱形 沿 轴正方向平移的距离.
答案
1.B 2.B 3.B 4.B 5.C 6.B 7.D 8.C 9.C 10.C
11.减小 [解析]因为反比例函数y=的图象经过点(2,3),所以k=2×3=6>0,
所以在这个函数图象所在的每一个象限内,y的值随x值的增大而减小.
故答案为减小.
12.
13.
14.
15.y=
16 【答案】
(1) .
(2) .
(3) .
17 【答案】
(1) 根据反比例函数的图象关于原点对称知,该函数图象的另一支在第三象限,且 ,则 .
(2) 点 与点 关于 轴对称,若 的面积为 ,
的面积为 .
设 ,则 ,
解得 .
18. 【答案】
(1) 如图,过点 作 轴的垂线,垂足为 .
因为点 的坐标为 ,
所以 ,.
所以 .
所以 .
所以点 的坐标为 .
所以 .
(2) 如图,将菱形 沿 轴正方向平移,使得点 落在函数 的图象上的 处,过点 作 轴的垂线,垂足为 .
因为 ,
所以 .
所以点 的纵坐标为 .
因为点 在 的图象上,
所以 ,解得 ,即 .
所以 .
所以菱形 沿 轴正方向平移的距离为 .
一、选择题
1.反比例函数y=的图象在 ( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
2.如图,在同一平面直角坐标系中,反比例函数与一次函数y=kx 1(k为常数,且k≠0)的图象可能是( )
A.B.C. D.
3.如图,正比例函数的图象与反比例函数的图象交于,两点,,两边分别交轴,轴于点,,四边形的面积为,轴于点.有下列结论:①;②三角形的面积为;③线段的长为;④不等式的解集是或.其中正确结论的个数是( ).
A. B. C. D.
4.某数学小组在研究了函数y1=x与y2=性质的基础上,进一步探究函数y=y1+y2的性质,经过讨论得到以下几个结论:①函数y=y1+y2的图象与直线y=3没有交点;②函数y=y1+y2的图象与直线y=a只有一个交点,则a=±4;③点(a,b)在函数y=y1+y2的图象上,则点(-a,-b)也在函数y=y1+y2的图象上.以上结论正确的是( )
A.①② B.①②③ C.②③ D.①③
5.下列给出的函数中,其图象是中心对称图形的是 ( )
①y=x; ②y=x2; ③y=.
A.①② B.②③ C.①③ D.都不是
6.如图,已知直线y=k1x(k1≠0)与反比例函数y=的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是 ( )
A.(-1,-2) B.(-1,2) C.(1,-2) D.(-2,-1)
7. 如图,反比例函数(k<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A. B. C. D.
8. 如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A. B. 10 C. D.
9. 如图直角三角板∠ABO=30°,直角项点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数的y1=图象上,顶点B在函数y2=的图象上,则=( )
A. B. C. D.
10.若函数y=(k≠0)与y=ax2+bx+c(a≠0)的图象如图所示,则函数y=kx+b的大致图象为 ( )
二、填空题
11.如果反比例函数y=的图象经过点(2,3),那么在这个函数图象所在的每一个象限内,y的值随x值的增大而 .(填“增大”或“减小”)
12.如图,双曲线经过矩形的顶点,双曲线交,于点,且与矩形的对角线交于点,连接,若,则的面积为______.
13.如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数y=(x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=,则k=_____.
14.如图,函数,,,的图象围成阴影部分的面积是___________.
15.如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y=的解析式为_____.
三、解答题
16作出反比例函数 的图象,并结合图象回答:
(1) 当 时, 的值;
(2) 当 时, 的取值范围;
(3) 当 时, 的取值范围.
17已知反比例函数 的图象的一支位于第一象限.
(1) 判断该函数图象的另一支所在的象限,并求 的取值范围;
(2) 如图, 为坐标原点,点 在该反比例函数位于第一象限的图象上,点 与点 关于 轴对称,若 的面积为 ,求 的值.
18如图,在平面直角坐标系中,菱形 的顶点 与原点 重合,点 在 轴的正半轴上,点 在函数 的图象上,点 的坐标为 .
(1) 求 的值;
(2) 若将菱形 沿 轴正方向平移,当菱形的顶点 落在函数 的图象上时,求菱形 沿 轴正方向平移的距离.
答案
1.B 2.B 3.B 4.B 5.C 6.B 7.D 8.C 9.C 10.C
11.减小 [解析]因为反比例函数y=的图象经过点(2,3),所以k=2×3=6>0,
所以在这个函数图象所在的每一个象限内,y的值随x值的增大而减小.
故答案为减小.
12.
13.
14.
15.y=
16 【答案】
(1) .
(2) .
(3) .
17 【答案】
(1) 根据反比例函数的图象关于原点对称知,该函数图象的另一支在第三象限,且 ,则 .
(2) 点 与点 关于 轴对称,若 的面积为 ,
的面积为 .
设 ,则 ,
解得 .
18. 【答案】
(1) 如图,过点 作 轴的垂线,垂足为 .
因为点 的坐标为 ,
所以 ,.
所以 .
所以 .
所以点 的坐标为 .
所以 .
(2) 如图,将菱形 沿 轴正方向平移,使得点 落在函数 的图象上的 处,过点 作 轴的垂线,垂足为 .
因为 ,
所以 .
所以点 的纵坐标为 .
因为点 在 的图象上,
所以 ,解得 ,即 .
所以 .
所以菱形 沿 轴正方向平移的距离为 .
