2021-2022学年人教版九年级数学下册26.1.2反比例函数图像和性质课后练习(word版、含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册26.1.2反比例函数图像和性质课后练习(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 269.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-30 20:34:27 | ||
图片预览

文档简介
26.1.2反比例函数图像和性质课后练习
一、选择题
1.关于反比例函数y=﹣,下列叙述正确的是( )
A.函数图象经过点(﹣2,﹣3) B.函数图象在第一、三象限
C.当x>﹣2时,y>3 D.当x<0时,y随x的增大而增大
2在反比例函数 的图象的每一条曲线上, 都随 的增大而减小,则 的取值范围是
A. B. C. D.
3下列反比例函数的图象一定在第一,三象限的是
A. B. C. D.
4已知函数 的图象经过点 ,下列说法正确的是
A. 随 的增大而增大
B.函数的图象只在第一象限
C.当 时,必有
D.点 不在此函数图象上
5.已知点A(﹣1,y1),B(1,y2),C(2,y3)是函数y=图象上的三点,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.无法确定
6.如图,在平面直角坐标系中,点的坐标为,轴于点,点是线段上的点,连接.点在线段上,且,函数的图象经过点.当点在线段上运动时,的取值范围是( )
A. B. C. D.
7.一次函数y=ax+b与反比例函数y=,其中ab<0,a,b为常数,它们在同一坐标系中的图象可以是( )
8.a,b是实数,点A(2,a),B(3,b)在反比例函数y=-的图象上,则( )
A.a<b<0 B.b<a<0 C.a<0<b D.b<0<a
9.已知正比例函数y=k1x和反比例函数y=,在同一直角坐标系下的图象如图所示,其中符合k1·k2>0的是( )
A.①② B.①④ C.②③ D.③④
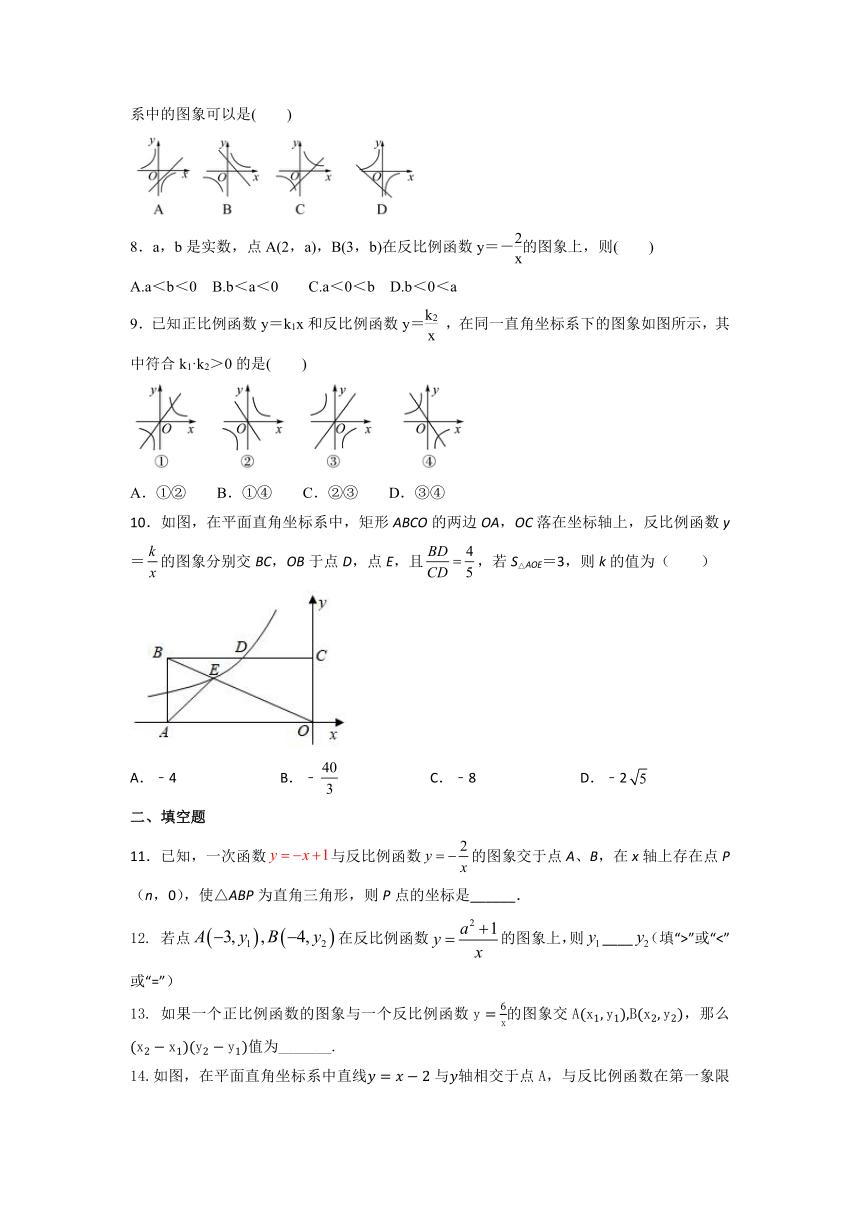
10.如图,在平面直角坐标系中,矩形ABCO的两边OA,OC落在坐标轴上,反比例函数y=的图象分别交BC,OB于点D,点E,且,若S△AOE=3,则k的值为( )
A.﹣4 B.﹣ C.﹣8 D.﹣2
二、填空题
11.已知,一次函数与反比例函数的图象交于点A、B,在x轴上存在点P(n,0),使△ABP为直角三角形,则P点的坐标是______.
12. 若点在反比例函数的图象上,则____(填“>”或“<”或“=”)
13. 如果一个正比例函数的图象与一个反比例函数的图象交,那么值为_______.
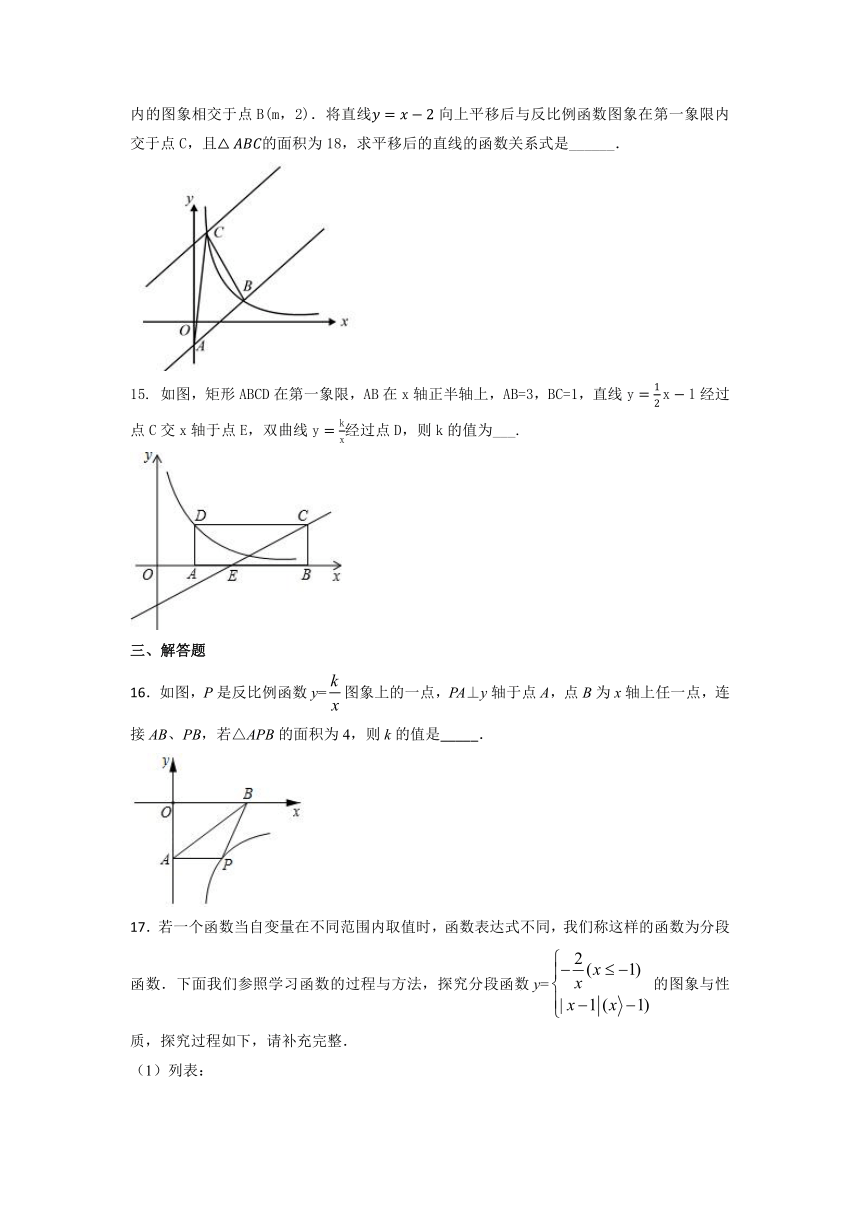
14.如图,在平面直角坐标系中直线与轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线向上平移后与反比例函数图象在第一象限内交于点C,且的面积为18,求平移后的直线的函数关系式是______.
15. 如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线经过点C交x轴于点E,双曲线经过点D,则k的值为___.
三、解答题
16.如图,P是反比例函数y=图象上的一点,PA⊥y轴于点A,点B为x轴上任一点,连接AB、PB,若△APB的面积为4,则k的值是_____.
17.若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数y=的图象与性质,探究过程如下,请补充完整.
(1)列表:
x … ﹣3 ﹣ 12 ﹣ ﹣1 ﹣ 0 1 2 3 …
y … m 1 2 1 0 1 n …
其中,m= ,n= .
(2)描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示,请画出函数的图象.
(3)研究函数并结合图象与表格,回答下列问题:
①点A(﹣6,y1),B(﹣,y2),C(x1,),D(x2,6)在函数图象上,则y y2,x1 x2;(填“>”,“=”或“<”)
②当函数值y=1时,求自变量x的值;
(4)若直线y=x+b与函数图象有且只有一个交点,请直接写出b的取值范围.
18.当值相同时,我们把正比例函数与反比例函数叫做“关联函数",可以通过图象研究“关联函数”的性质.小明根据学习函数的经验,先以与为例对“关联函数”进行了探究.下面是小明的探究过程,请你将它补充完整;
(1)如图,在同一坐标系中画出这两个函数的图象.设这两个函数图象的交点分别为A,B,则点A的坐标为(-2,-1),点B的坐标为_______.
(2)点是函数在第一象限内的图象上一个动点(点不与点重合),设点的坐标为,其中且.
①结论1:作直线分别与轴交于点,则在点运动的过程中,总有.
证明:设直线的解析式为,将点和点的坐标代入,得,解得
则直线的解析式为,令,可得,则点的坐标为,同理可求,直线的解析式为,点的坐标为_________.
请你继续完成证明的后续过程:
②结论2:设的面积为,则是的函数.请你直接写出与的函数表达式.
19.如图,在平面直角坐标系中,的顶点,在函数的图象上,过点作轴交于点.
(1)求的值和直线的解析式;
(2)若点的横坐标为2,求的面积.
20.如图,已知一次函数与反比例函数的图象交于和两点,与x轴交于点M.
(1)求反比例函数的解析式;
(2)求的面积;
(3)根据图象直接写出反比例函数值大于一次函数值吋x的取值范围.
21.如图,在平面直角坐标系内,双曲线上有A,B两点,且与直线交于第一象限内的点A,点A的坐标为,点B的坐标为,过点B作y轴的平行线,交x轴于点C,交直线与点D.
(1)求:点D的坐标;
(2)求:的面积;
(3)在x轴正半轴上是否存在点P,使是以OA为腰的等腰三角形?若不存在,请说明理由;若存在,请直接写出P的坐标.
【参考答案】
1.D 2.A 3.C 4.C 5.B 6.D 7.C 8.A B 9.C 10.D
11.(3,0)或(-3,0)或或
12. 答案:
13. 答案:.
14.答案:y=x+7.
15. 答案:1.
16.﹣8.
17.(1),2;(2)略;(3)①<,<;②x=0或x=2或x=﹣2;(4)﹣1<b<2或b>3.
18.(1);(2)①,;证明略;②.
19.(1),;(2)
20.(1)(2)4(3)-2<x<0或x>4
21.(1)点D坐标为;(2);(3)存在,,.
一、选择题
1.关于反比例函数y=﹣,下列叙述正确的是( )
A.函数图象经过点(﹣2,﹣3) B.函数图象在第一、三象限
C.当x>﹣2时,y>3 D.当x<0时,y随x的增大而增大
2在反比例函数 的图象的每一条曲线上, 都随 的增大而减小,则 的取值范围是
A. B. C. D.
3下列反比例函数的图象一定在第一,三象限的是
A. B. C. D.
4已知函数 的图象经过点 ,下列说法正确的是
A. 随 的增大而增大
B.函数的图象只在第一象限
C.当 时,必有
D.点 不在此函数图象上
5.已知点A(﹣1,y1),B(1,y2),C(2,y3)是函数y=图象上的三点,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.无法确定
6.如图,在平面直角坐标系中,点的坐标为,轴于点,点是线段上的点,连接.点在线段上,且,函数的图象经过点.当点在线段上运动时,的取值范围是( )
A. B. C. D.
7.一次函数y=ax+b与反比例函数y=,其中ab<0,a,b为常数,它们在同一坐标系中的图象可以是( )
8.a,b是实数,点A(2,a),B(3,b)在反比例函数y=-的图象上,则( )
A.a<b<0 B.b<a<0 C.a<0<b D.b<0<a
9.已知正比例函数y=k1x和反比例函数y=,在同一直角坐标系下的图象如图所示,其中符合k1·k2>0的是( )
A.①② B.①④ C.②③ D.③④
10.如图,在平面直角坐标系中,矩形ABCO的两边OA,OC落在坐标轴上,反比例函数y=的图象分别交BC,OB于点D,点E,且,若S△AOE=3,则k的值为( )
A.﹣4 B.﹣ C.﹣8 D.﹣2
二、填空题
11.已知,一次函数与反比例函数的图象交于点A、B,在x轴上存在点P(n,0),使△ABP为直角三角形,则P点的坐标是______.
12. 若点在反比例函数的图象上,则____(填“>”或“<”或“=”)
13. 如果一个正比例函数的图象与一个反比例函数的图象交,那么值为_______.
14.如图,在平面直角坐标系中直线与轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线向上平移后与反比例函数图象在第一象限内交于点C,且的面积为18,求平移后的直线的函数关系式是______.
15. 如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线经过点C交x轴于点E,双曲线经过点D,则k的值为___.
三、解答题
16.如图,P是反比例函数y=图象上的一点,PA⊥y轴于点A,点B为x轴上任一点,连接AB、PB,若△APB的面积为4,则k的值是_____.
17.若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数y=的图象与性质,探究过程如下,请补充完整.
(1)列表:
x … ﹣3 ﹣ 12 ﹣ ﹣1 ﹣ 0 1 2 3 …
y … m 1 2 1 0 1 n …
其中,m= ,n= .
(2)描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示,请画出函数的图象.
(3)研究函数并结合图象与表格,回答下列问题:
①点A(﹣6,y1),B(﹣,y2),C(x1,),D(x2,6)在函数图象上,则y y2,x1 x2;(填“>”,“=”或“<”)
②当函数值y=1时,求自变量x的值;
(4)若直线y=x+b与函数图象有且只有一个交点,请直接写出b的取值范围.
18.当值相同时,我们把正比例函数与反比例函数叫做“关联函数",可以通过图象研究“关联函数”的性质.小明根据学习函数的经验,先以与为例对“关联函数”进行了探究.下面是小明的探究过程,请你将它补充完整;
(1)如图,在同一坐标系中画出这两个函数的图象.设这两个函数图象的交点分别为A,B,则点A的坐标为(-2,-1),点B的坐标为_______.
(2)点是函数在第一象限内的图象上一个动点(点不与点重合),设点的坐标为,其中且.
①结论1:作直线分别与轴交于点,则在点运动的过程中,总有.
证明:设直线的解析式为,将点和点的坐标代入,得,解得
则直线的解析式为,令,可得,则点的坐标为,同理可求,直线的解析式为,点的坐标为_________.
请你继续完成证明的后续过程:
②结论2:设的面积为,则是的函数.请你直接写出与的函数表达式.
19.如图,在平面直角坐标系中,的顶点,在函数的图象上,过点作轴交于点.
(1)求的值和直线的解析式;
(2)若点的横坐标为2,求的面积.
20.如图,已知一次函数与反比例函数的图象交于和两点,与x轴交于点M.
(1)求反比例函数的解析式;
(2)求的面积;
(3)根据图象直接写出反比例函数值大于一次函数值吋x的取值范围.
21.如图,在平面直角坐标系内,双曲线上有A,B两点,且与直线交于第一象限内的点A,点A的坐标为,点B的坐标为,过点B作y轴的平行线,交x轴于点C,交直线与点D.
(1)求:点D的坐标;
(2)求:的面积;
(3)在x轴正半轴上是否存在点P,使是以OA为腰的等腰三角形?若不存在,请说明理由;若存在,请直接写出P的坐标.
【参考答案】
1.D 2.A 3.C 4.C 5.B 6.D 7.C 8.A B 9.C 10.D
11.(3,0)或(-3,0)或或
12. 答案:
13. 答案:.
14.答案:y=x+7.
15. 答案:1.
16.﹣8.
17.(1),2;(2)略;(3)①<,<;②x=0或x=2或x=﹣2;(4)﹣1<b<2或b>3.
18.(1);(2)①,;证明略;②.
19.(1),;(2)
20.(1)(2)4(3)-2<x<0或x>4
21.(1)点D坐标为;(2);(3)存在,,.
