小学数学北师大新版下学期四年级同步作业2.认识三角形和四边形(带答案和解析)
文档属性
| 名称 | 小学数学北师大新版下学期四年级同步作业2.认识三角形和四边形(带答案和解析) |  | |
| 格式 | docx | ||
| 文件大小 | 81.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 11:06:58 | ||
图片预览


文档简介
2021-2022学年下学期小学数学北师大新版四年级同步作业
2.认识三角形和四边形
一.选择题(共4小题)
1.下面图形不是四边形的是( )
A. B. C.
2.等边三角形一定是( )三角形.
A.锐角 B.直角 C.钝角
3.将一根长20厘米的细铁丝,剪成3段,拼成一个三角形,以下( )剪法是可以的。
A.8厘米,7厘米,5厘米 B.6厘米,13厘米,5厘米
C.2厘米,9厘米,6厘米 D.10厘米,3厘米,7厘米
4.被遮住的三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
二.填空题(共5小题)
5.学校大门做成的伸缩门,这是应用了平行四边形的 的特性.
6.一个平行四边形的三条边分别长3cm,5cm,3cm,那么第四条边长 。
7.小红用一根1米长的铁丝,围成一个三角形,量得三角形一边长0.27米,另一边长0.46米,第三边长 米,这是一个 三角形。
8.把一个三角形分成两个小三角形,每个小三角形的内角和是 °
9.如图,∠C= 。
三.操作题
四.解答题(共2小题)
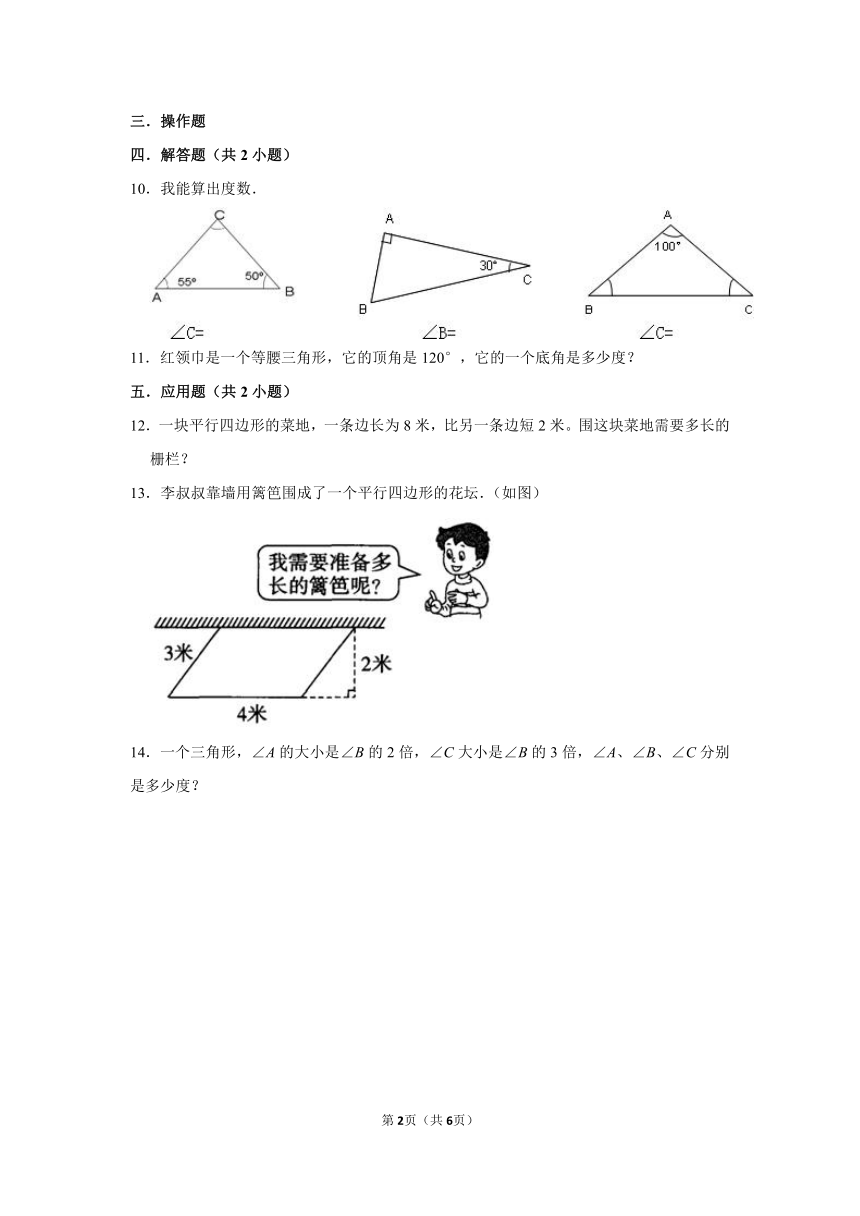
10.我能算出度数.
11.红领巾是一个等腰三角形,它的顶角是120°,它的一个底角是多少度?
五.应用题(共2小题)
12.一块平行四边形的菜地,一条边长为8米,比另一条边短2米。围这块菜地需要多长的栅栏?
13.李叔叔靠墙用篱笆围成了一个平行四边形的花坛.(如图)
14.一个三角形,∠A的大小是∠B的2倍,∠C大小是∠B的3倍,∠A、∠B、∠C分别是多少度?
2021-2022学年下学期小学数学北师大新版四年级同步作业
2.认识三角形和四边形
参考答案与试题解析
一.选择题(共4小题)
1.【分析】四边形的特点:四边形就是四条线段围成的图形,有四条边,四个角,且内角和是360°;据此解答即可.
【解答】解:选项AC都是四边形,选项B是五边形不是四边形;
故选:B.
【点评】解答此题应根据四边形的含义和特征进行解答.
2.【分析】等边三角形的三个角都相等,都是60°,由此根据三角形按角分类的方法即可进行选择.
【解答】解:等边三角形的三个角都是60°,都是锐角,所以等边三角形是锐角三角形.
故选:A。
【点评】抓住等边三角形的三个角都相等的性质和锐角三角形的定义即可解决问题.
3.【分析】三角形的任意两边的和必须大于第三边,据此计算出两条短边的和与最长边作比较即可。
【解答】解:7+5=12,12>8,可以拼成一个三角形;
6+5=11,11<13,不可以拼成三角形;
2+6=8,8<9,所以不可以拼成三角形;
3+7=10,10=10,因此不能拼成三角形。
故选:A。
【点评】本题考查了三角形的三边关系,两边之和必须大于第三边。
4.【分析】根据三角形按照角的大小分类:三个角都是锐角的三角形叫做锐角三角形;有一个角是直角的三角形叫做直角三角形;有一个角是钝角的三角形叫做钝角三角形.只要确定被遮挡的角是什么角,就可以确定这个三角形属于哪一种三角形.
【解答】解:显然被遮挡的角是钝角,所以这个三角形是钝角三角形.
故选:C.
【点评】此题考查的目的是理解掌握三角形按照角的大小分类的情况及应用.
二.填空题(共5小题)
5.【分析】学校大门做成的伸缩门,这是应用了平行四边形不稳定性进行制作的,便于伸缩.
【解答】解:根据生活的需要,学校大门做成的伸缩门,
这是应用了平行四边形不稳定性制作的.
故答案为:不稳定.
【点评】学校大门做成的伸缩门,这是应用了平行四边形不稳定性制作的,考查了四边形的特征.
6.【分析】根据平行四边形的对边相等,解答此题即可。
【解答】解:一个平行四边形的三条边分别长3cm,5cm,3cm,那么第四条边长5cm。
故答案为:5cm。
【点评】熟练掌握平行四边形的性质,是解答此题的关键。
7.【分析】用铁丝总长度减去两边的长度即可求出第三边长;进而根据边的长度关系判断三角形分类即可。
【解答】解:1﹣0.27﹣0.46
=0.73﹣0.46
=0.27(米)
第三边长0.27米,这是一个等腰三角形。
故答案为:0.27,等腰。
【点评】此题主要考查了三角形的分类方法,要熟练掌握。
8.【分析】根据任何三角形的内角和都等于180°,解答此题即可。
【解答】解:把一个三角形分成两个小三角形,每个小三角形的内角和是180°。
故答案为:180。
【点评】熟练掌握三角形的内角和的知识,是解答此题的关键。
9.【分析】根据三角形的内角和等于180度,解答此题即可。
【解答】解:180°﹣90°﹣35°=55°
答:∠C=55°。
故答案为:55°。
【点评】熟练掌握三角形的内角和知识,是解答此题的关键。
三.操作题
四.解答题(共2小题)
10.【分析】因为三角形的内角和是180度,所以用180度,减去已知的两个角的度数,即可求出三角形的第三个角的度数,据此即可解答问题.
【解答】解:(1)180°﹣55°﹣50°=75°
(2)180°﹣90°﹣30°=60°
(3)(180°﹣100°)÷2
=80°÷2
=40°
故答案为:
【点评】此题考查了三角形内角和定理的实际应用.
11.【分析】因为三角形的内角和是180度,又因为等腰三角形的两个底角相等,用“180°﹣120°=60°”求出两个底角的度数,再用“60°÷2=30°”求出一个底角的度数.
【解答】解:(180°﹣120°)÷2
=60°÷2
=30°
答:它的一个底角是30度.
【点评】本题考查了三角形的内角和是180°和等腰三角形2个底角是相等的,运用内角和求角即可.
五.应用题(共2小题)
12.【分析】平行四边形的两组对边分别相等,据此求出相邻的两条边的和,再乘2即可得出平行四边形的周长,即围这块菜地需要的栅栏长。
【解答】解:(8+8+2)×2
=18×2
=36(米)
答:围这块菜地需要36米长栅栏。
【点评】此题主要考查平行四边形的周长的计算应用。
13.【分析】观察图可知,这个平行四边形的一条边靠墙,只要求出另外三边的和,就是需要准备篱笆的长度.
【解答】解:4+3+3=10(米)
答:李叔叔需要准备10米长的篱笆.
【点评】本题根据平行四边形的特点求解,注意给出的高2米没有用处,不要被迷惑.
14.【分析】根据题意,设∠B是x度,则∠A的度数是2x度,∠C是3x度,然后根据三角形的内角和是180°,列出方程解答即可.
【解答】解:设∠B是x度,则∠A的度数是2x度,∠C是3x度,
x+2x+3x=180°
6x=180°
x=30°
30°×2=60°
30°×3=90°
答:∠A=60°,∠B=30°,∠C=90°.
【点评】此题考查根据三角形三个角的关系和三角形的内角和是180°,求其中的一个角的度数.
第2页(共2页)
2.认识三角形和四边形
一.选择题(共4小题)
1.下面图形不是四边形的是( )
A. B. C.
2.等边三角形一定是( )三角形.
A.锐角 B.直角 C.钝角
3.将一根长20厘米的细铁丝,剪成3段,拼成一个三角形,以下( )剪法是可以的。
A.8厘米,7厘米,5厘米 B.6厘米,13厘米,5厘米
C.2厘米,9厘米,6厘米 D.10厘米,3厘米,7厘米
4.被遮住的三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
二.填空题(共5小题)
5.学校大门做成的伸缩门,这是应用了平行四边形的 的特性.
6.一个平行四边形的三条边分别长3cm,5cm,3cm,那么第四条边长 。
7.小红用一根1米长的铁丝,围成一个三角形,量得三角形一边长0.27米,另一边长0.46米,第三边长 米,这是一个 三角形。
8.把一个三角形分成两个小三角形,每个小三角形的内角和是 °
9.如图,∠C= 。
三.操作题
四.解答题(共2小题)
10.我能算出度数.
11.红领巾是一个等腰三角形,它的顶角是120°,它的一个底角是多少度?
五.应用题(共2小题)
12.一块平行四边形的菜地,一条边长为8米,比另一条边短2米。围这块菜地需要多长的栅栏?
13.李叔叔靠墙用篱笆围成了一个平行四边形的花坛.(如图)
14.一个三角形,∠A的大小是∠B的2倍,∠C大小是∠B的3倍,∠A、∠B、∠C分别是多少度?
2021-2022学年下学期小学数学北师大新版四年级同步作业
2.认识三角形和四边形
参考答案与试题解析
一.选择题(共4小题)
1.【分析】四边形的特点:四边形就是四条线段围成的图形,有四条边,四个角,且内角和是360°;据此解答即可.
【解答】解:选项AC都是四边形,选项B是五边形不是四边形;
故选:B.
【点评】解答此题应根据四边形的含义和特征进行解答.
2.【分析】等边三角形的三个角都相等,都是60°,由此根据三角形按角分类的方法即可进行选择.
【解答】解:等边三角形的三个角都是60°,都是锐角,所以等边三角形是锐角三角形.
故选:A。
【点评】抓住等边三角形的三个角都相等的性质和锐角三角形的定义即可解决问题.
3.【分析】三角形的任意两边的和必须大于第三边,据此计算出两条短边的和与最长边作比较即可。
【解答】解:7+5=12,12>8,可以拼成一个三角形;
6+5=11,11<13,不可以拼成三角形;
2+6=8,8<9,所以不可以拼成三角形;
3+7=10,10=10,因此不能拼成三角形。
故选:A。
【点评】本题考查了三角形的三边关系,两边之和必须大于第三边。
4.【分析】根据三角形按照角的大小分类:三个角都是锐角的三角形叫做锐角三角形;有一个角是直角的三角形叫做直角三角形;有一个角是钝角的三角形叫做钝角三角形.只要确定被遮挡的角是什么角,就可以确定这个三角形属于哪一种三角形.
【解答】解:显然被遮挡的角是钝角,所以这个三角形是钝角三角形.
故选:C.
【点评】此题考查的目的是理解掌握三角形按照角的大小分类的情况及应用.
二.填空题(共5小题)
5.【分析】学校大门做成的伸缩门,这是应用了平行四边形不稳定性进行制作的,便于伸缩.
【解答】解:根据生活的需要,学校大门做成的伸缩门,
这是应用了平行四边形不稳定性制作的.
故答案为:不稳定.
【点评】学校大门做成的伸缩门,这是应用了平行四边形不稳定性制作的,考查了四边形的特征.
6.【分析】根据平行四边形的对边相等,解答此题即可。
【解答】解:一个平行四边形的三条边分别长3cm,5cm,3cm,那么第四条边长5cm。
故答案为:5cm。
【点评】熟练掌握平行四边形的性质,是解答此题的关键。
7.【分析】用铁丝总长度减去两边的长度即可求出第三边长;进而根据边的长度关系判断三角形分类即可。
【解答】解:1﹣0.27﹣0.46
=0.73﹣0.46
=0.27(米)
第三边长0.27米,这是一个等腰三角形。
故答案为:0.27,等腰。
【点评】此题主要考查了三角形的分类方法,要熟练掌握。
8.【分析】根据任何三角形的内角和都等于180°,解答此题即可。
【解答】解:把一个三角形分成两个小三角形,每个小三角形的内角和是180°。
故答案为:180。
【点评】熟练掌握三角形的内角和的知识,是解答此题的关键。
9.【分析】根据三角形的内角和等于180度,解答此题即可。
【解答】解:180°﹣90°﹣35°=55°
答:∠C=55°。
故答案为:55°。
【点评】熟练掌握三角形的内角和知识,是解答此题的关键。
三.操作题
四.解答题(共2小题)
10.【分析】因为三角形的内角和是180度,所以用180度,减去已知的两个角的度数,即可求出三角形的第三个角的度数,据此即可解答问题.
【解答】解:(1)180°﹣55°﹣50°=75°
(2)180°﹣90°﹣30°=60°
(3)(180°﹣100°)÷2
=80°÷2
=40°
故答案为:
【点评】此题考查了三角形内角和定理的实际应用.
11.【分析】因为三角形的内角和是180度,又因为等腰三角形的两个底角相等,用“180°﹣120°=60°”求出两个底角的度数,再用“60°÷2=30°”求出一个底角的度数.
【解答】解:(180°﹣120°)÷2
=60°÷2
=30°
答:它的一个底角是30度.
【点评】本题考查了三角形的内角和是180°和等腰三角形2个底角是相等的,运用内角和求角即可.
五.应用题(共2小题)
12.【分析】平行四边形的两组对边分别相等,据此求出相邻的两条边的和,再乘2即可得出平行四边形的周长,即围这块菜地需要的栅栏长。
【解答】解:(8+8+2)×2
=18×2
=36(米)
答:围这块菜地需要36米长栅栏。
【点评】此题主要考查平行四边形的周长的计算应用。
13.【分析】观察图可知,这个平行四边形的一条边靠墙,只要求出另外三边的和,就是需要准备篱笆的长度.
【解答】解:4+3+3=10(米)
答:李叔叔需要准备10米长的篱笆.
【点评】本题根据平行四边形的特点求解,注意给出的高2米没有用处,不要被迷惑.
14.【分析】根据题意,设∠B是x度,则∠A的度数是2x度,∠C是3x度,然后根据三角形的内角和是180°,列出方程解答即可.
【解答】解:设∠B是x度,则∠A的度数是2x度,∠C是3x度,
x+2x+3x=180°
6x=180°
x=30°
30°×2=60°
30°×3=90°
答:∠A=60°,∠B=30°,∠C=90°.
【点评】此题考查根据三角形三个角的关系和三角形的内角和是180°,求其中的一个角的度数.
第2页(共2页)
