小学数学冀教版五年级下册数学课件-四 分数乘法 倒数的认识 (26张ppt)
文档属性
| 名称 | 小学数学冀教版五年级下册数学课件-四 分数乘法 倒数的认识 (26张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 12:00:13 | ||
图片预览






文档简介
(共26张PPT)
倒数的认识
学习目标
2.学习求一个数的倒数的方法,能正确地求一个数的倒数。
1.能够理解和掌握倒数的意义。
3.体会事物之间相互依存的关系。
口算下面各题。
×
3
8
8
3
=
1
×
7
15
15
7
=
1
5×
5
1
=
1
×12
12
1
=
1
1
×
6
13
13
6
=
1
×
2
9
9
2
=
绿色圃中小学教育网http://www.lspjy.com
绿色圃中小学教育网http://www.lspjy.com
复习导入
观察每一对数字,你发现了什么?
乘积是1的两个数互为倒数。
3
1
8
1
60
1
2
3
3
2
4
5
5
4
7
9
9
7
1和
8和
60和
和
和
和
1
探索新知
像这样乘积是1的数字
有多少对呢?
“0”有没有这样的数呢?
探索新知
2
3
3
2
4
5
5
4
7
9
9
7
和
和
和
两个数的分子和分母交换了位置。
像这样的每组数都有什么特点呢?
探索新知
7
2
5
3
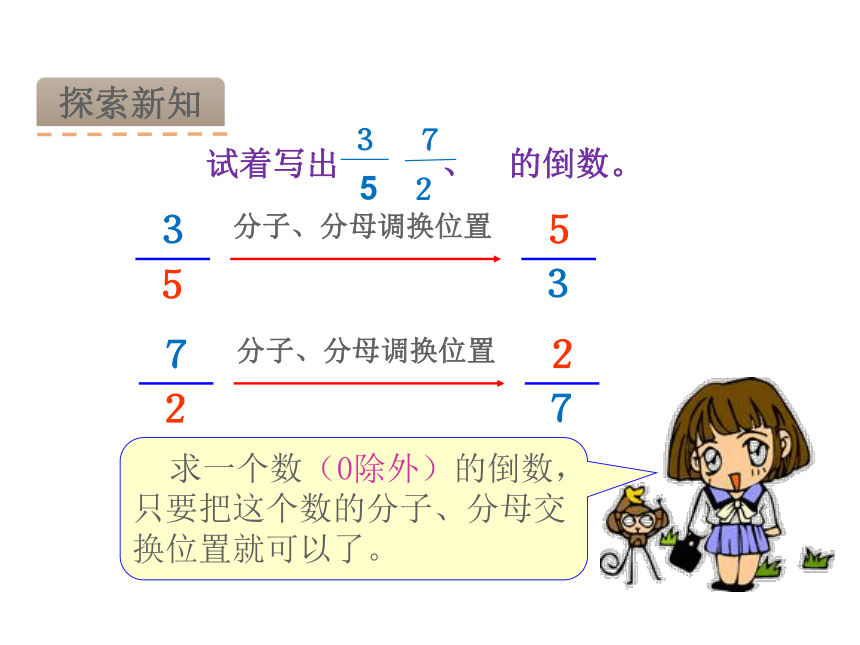
试着写出 、 的倒数。
3
5
5
3
分子、分母调换位置
7
2
2
7
分子、分母调换位置
求一个数(0除外)的倒数,只要把这个数的分子、分母交换位置就可以了。
探索新知
⑴
真分数的倒数一定大于 1 。
4
3
5
1
9
7
先找出每组数中各数的倒数,再看看能发现什么
5
探索新知
假分数的倒数等于或小于 1 。
⑵
2
7
5
9
6
6
先找出每组数中各数的倒数,再看看能发现什么
1
探索新知
整数(0除外)的倒数的分子一定是 1 。
(3)
1
4
1
9
1
15
先找出每组数中各数的倒数,再看看能发现什么
探索新知
典题精讲
如果x是非0自然数,下面说法对的画“√”,错的画“ ”。
(1)x是倒数。 ( )
(2)x和都是倒数。 ( )
(3)x和互为倒数。 ( )
典题精讲
解题思路:
根据倒数的概念来判断。理解倒数的概念需注意两点:一是倒数表示两个数之间的关系,单独一个数不能称为倒数;二是两个数的乘积是1。
典题精讲
正确解答:
如果x是非0自然数,下面说法对的画“√”,错的画“ ”。
(1)x是倒数。 (×)
(2)x和都是倒数。(×)
(3)x和互为倒数。(√)
典题精讲
如果a×=b×=1,那么7a+11b等于多少
典题精讲
解题思路:
因为a×=1,根据“乘积是1的两个数互为倒数”,所以a和互为倒数,这样可以得到a的值。同理也可以得到b的值。将a和b的值代入7a+11b中,算出结果即可。
典题精讲
正确解答:
因为a×=b×=1,所以a=,b=。7a+11b=7×+11×=12+6=18
判断:1的倒数是1,0的倒数是0。 ( )
易错提醒
错误解答
√
错解分析:
易错提醒
错误解答错在“0的倒数是0”。因为“乘积是1的两个数互为倒数”,而0和任何数相乘都得0,不等于1,所以0没有倒数。
易错提醒
正确解答
错误解答
判断:1的倒数是1,0的倒数是0。 ( )
√
判断:1的倒数是1,0的倒数是0。 ( )
×
填一填
4
7
×
( )
( )
=
1
×
( )
( )
=
1
9
3
5
×
( )
( )
=
1
1
4
7
9
1
8
5
学以致用
3
8
8
3
5
2
11
3
3
11
1
6
2
5
6
0
学以致用
连一连
写出上面各数的倒数。
3
12
1
6
7
20
14
3
1
9
9
10
1
3
学以致用
因为 ,
所以 是倒数。
× =1
4
5
5
4
5
4
因为 ,
所以 是倒数。
× =1
4
5
5
4
5
4
×
因为 ,
所以 和 互为倒数。
× =1
3
5
5
3
3
5
5
3
因为 ,
所以 和 互为倒数。
× =1
3
5
5
3
3
5
5
3
√
1的倒数是1,
0的倒数是0。
1的倒数是1,
0的倒数是0。
×
学以致用
这些数怎样求倒数呢?
1
2
2
3
1
0.4
1
1
=
1
2
=
3
7
=
5
2
=
整数、带分数、小数都化成
真分数或假分数形式,再把分子、
分母调换位置。
学以致用
课堂小结
2.找一个数的倒数的方法:
①找真分数、假分数的倒数:交换分子、分母的位置。②找整数的倒数:先把整数看作分母是1的分数,再交换分子、分母的位置。③找小数的倒数:可以先把它化成分数,再调换分子、分母的位置;也可以直接用1除以这个数,并写成分数的形式。④1的倒数是1,0没有倒数。
你学会了哪些知识?
真分数的倒数都大于它本身,假分数的倒数等于或小于它本身。
1.乘积是1的两个数互为倒数。
谢谢
倒数的认识
学习目标
2.学习求一个数的倒数的方法,能正确地求一个数的倒数。
1.能够理解和掌握倒数的意义。
3.体会事物之间相互依存的关系。
口算下面各题。
×
3
8
8
3
=
1
×
7
15
15
7
=
1
5×
5
1
=
1
×12
12
1
=
1
1
×
6
13
13
6
=
1
×
2
9
9
2
=
绿色圃中小学教育网http://www.lspjy.com
绿色圃中小学教育网http://www.lspjy.com
复习导入
观察每一对数字,你发现了什么?
乘积是1的两个数互为倒数。
3
1
8
1
60
1
2
3
3
2
4
5
5
4
7
9
9
7
1和
8和
60和
和
和
和
1
探索新知
像这样乘积是1的数字
有多少对呢?
“0”有没有这样的数呢?
探索新知
2
3
3
2
4
5
5
4
7
9
9
7
和
和
和
两个数的分子和分母交换了位置。
像这样的每组数都有什么特点呢?
探索新知
7
2
5
3
试着写出 、 的倒数。
3
5
5
3
分子、分母调换位置
7
2
2
7
分子、分母调换位置
求一个数(0除外)的倒数,只要把这个数的分子、分母交换位置就可以了。
探索新知
⑴
真分数的倒数一定大于 1 。
4
3
5
1
9
7
先找出每组数中各数的倒数,再看看能发现什么
5
探索新知
假分数的倒数等于或小于 1 。
⑵
2
7
5
9
6
6
先找出每组数中各数的倒数,再看看能发现什么
1
探索新知
整数(0除外)的倒数的分子一定是 1 。
(3)
1
4
1
9
1
15
先找出每组数中各数的倒数,再看看能发现什么
探索新知
典题精讲
如果x是非0自然数,下面说法对的画“√”,错的画“ ”。
(1)x是倒数。 ( )
(2)x和都是倒数。 ( )
(3)x和互为倒数。 ( )
典题精讲
解题思路:
根据倒数的概念来判断。理解倒数的概念需注意两点:一是倒数表示两个数之间的关系,单独一个数不能称为倒数;二是两个数的乘积是1。
典题精讲
正确解答:
如果x是非0自然数,下面说法对的画“√”,错的画“ ”。
(1)x是倒数。 (×)
(2)x和都是倒数。(×)
(3)x和互为倒数。(√)
典题精讲
如果a×=b×=1,那么7a+11b等于多少
典题精讲
解题思路:
因为a×=1,根据“乘积是1的两个数互为倒数”,所以a和互为倒数,这样可以得到a的值。同理也可以得到b的值。将a和b的值代入7a+11b中,算出结果即可。
典题精讲
正确解答:
因为a×=b×=1,所以a=,b=。7a+11b=7×+11×=12+6=18
判断:1的倒数是1,0的倒数是0。 ( )
易错提醒
错误解答
√
错解分析:
易错提醒
错误解答错在“0的倒数是0”。因为“乘积是1的两个数互为倒数”,而0和任何数相乘都得0,不等于1,所以0没有倒数。
易错提醒
正确解答
错误解答
判断:1的倒数是1,0的倒数是0。 ( )
√
判断:1的倒数是1,0的倒数是0。 ( )
×
填一填
4
7
×
( )
( )
=
1
×
( )
( )
=
1
9
3
5
×
( )
( )
=
1
1
4
7
9
1
8
5
学以致用
3
8
8
3
5
2
11
3
3
11
1
6
2
5
6
0
学以致用
连一连
写出上面各数的倒数。
3
12
1
6
7
20
14
3
1
9
9
10
1
3
学以致用
因为 ,
所以 是倒数。
× =1
4
5
5
4
5
4
因为 ,
所以 是倒数。
× =1
4
5
5
4
5
4
×
因为 ,
所以 和 互为倒数。
× =1
3
5
5
3
3
5
5
3
因为 ,
所以 和 互为倒数。
× =1
3
5
5
3
3
5
5
3
√
1的倒数是1,
0的倒数是0。
1的倒数是1,
0的倒数是0。
×
学以致用
这些数怎样求倒数呢?
1
2
2
3
1
0.4
1
1
=
1
2
=
3
7
=
5
2
=
整数、带分数、小数都化成
真分数或假分数形式,再把分子、
分母调换位置。
学以致用
课堂小结
2.找一个数的倒数的方法:
①找真分数、假分数的倒数:交换分子、分母的位置。②找整数的倒数:先把整数看作分母是1的分数,再交换分子、分母的位置。③找小数的倒数:可以先把它化成分数,再调换分子、分母的位置;也可以直接用1除以这个数,并写成分数的形式。④1的倒数是1,0没有倒数。
你学会了哪些知识?
真分数的倒数都大于它本身,假分数的倒数等于或小于它本身。
1.乘积是1的两个数互为倒数。
谢谢
