2021-2022学年人教版九年级数学下册第二十七章 相似 单元测试训练卷(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十七章 相似 单元测试训练卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 133.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-31 10:25:58 | ||
图片预览



文档简介
人教版九年级数学下册
第二十七章 相似
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 在下列各组线段中,不成比例的是( )
A.a=3,b=6,c=2,d=4
B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=5,d=10
D.a=1,b=,c=,d=
2. 如图,在△ABC中,DE∥BC,=,则下列结论正确的是( )
A.= B.= C.= D.=
3. 如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,点O为位似中心,若OD=OD′,则A′B′∶AB为( )
A.2∶3 B.3∶2 C.1∶2 D.2∶1
4. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20 m,EC=10 m,CD=20 m,则河的宽度AB等于( )
A.60 m B.40 m C.30 m D.20 m
5. 如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E.若线段DE=5,则线段BC的长为( )
A.7.5 B.10 C.15 D.20
6. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5 cm,6 cm和9 cm,另一个三角形的最短边长为2.5 cm,则它的最长边为( )
A.3 cm B.4 cm C.4.5 cm D.5 cm
7. 如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
A.= B.= C.= D.=
8. 如图,在△ABC中,AB=7 cm,AC=4 cm,点D从B点以每秒2 cm的速度向点A移动,点E从A点以每秒1 cm的速度向点C移动,若D、E同时出发,同时停止且停止时△ADE与△ABC相似,则经过的时间是( )
A. s B. s C. s或 s D. s或 s
9.为了测量校园水平地面上一棵不可攀登的树的高度,学校数学兴趣小组做了如下探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子水平放置在离树8.4 m远的点E处,然后沿着直线BE走到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2 m,观察者眼高CD=1.6 m,则树AB的高度为( )
A.4.2 m B.4.8 m C.6.4 m D.16.8 m
10. 如图,AB是半圆O的直径,点C是的中点,点D是的中点,连接AC,BD交于点E,则等于( )
A. B. C.1- D.
二.填空题(共6小题,4*6=24)
11. 已知线段a,b,c,d成比例,且线段a=6,c=18,d=24,则b=__ __.
12. 如图,直线AD∥BE∥CF,BC=AC,DE=4,那么EF的值是________.
13. 如图,身高为1.7m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A、E、C′在一条线上.已知河BD的宽度为12m,BE=3m,则树CD的高为 .
14. 如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,CA′与AB的延长线相交于点D,则线段BD的长为__ __.
15.如图,有一个广告牌OE,小明站在距广告牌OE 10米远的A处恰好可以看到广告牌顶端,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则广告牌OE的高度为 米.
16.如图,四边形ABCD中,AD∥BC,CM是∠BCD的平分线,且CM⊥AB,M为垂足,AM=13AB.若四边形ABCD的面积为157,则四边形AMCD的面积是 .’
三.解答题(共5小题, 56分)
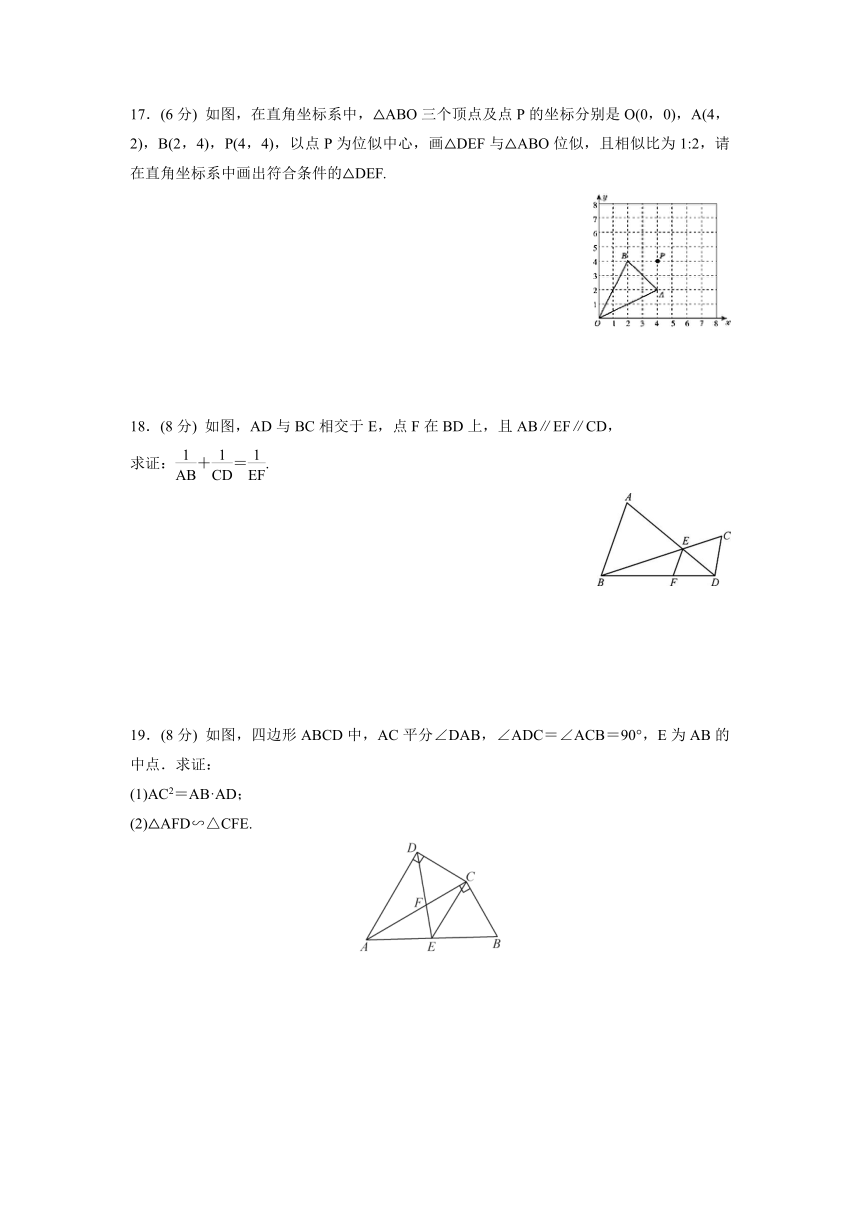
17.(6分) 如图,在直角坐标系中,△ABO三个顶点及点P的坐标分别是O(0,0),A(4,2),B(2,4),P(4,4),以点P为位似中心,画△DEF与△ABO位似,且相似比为1:2,请在直角坐标系中画出符合条件的△DEF.
18.(8分) 如图,AD与BC相交于E,点F在BD上,且AB∥EF∥CD,
求证:+=.
19.(8分) 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.求证:
(1)AC2=AB·AD;
(2)△AFD∽△CFE.
20.(10分) 如图,小明想测量河对岸建筑物AB的高度,在地面上C处放置了一块平面镜,然后从C点向后退了2.4米至D处,小明的眼睛E恰好看到了镜中建筑物A的像,在D处做好标记,将平面镜移至D处,小明再次从D点后退2.52米至F处,眼睛G恰好又看到了建筑物顶端A的像,已知小明眼睛距地面的高度ED,GF均为1.6米,求建筑物AB的高度.(注:图中的左侧α,β为入射角,右侧的α,β为反射角)
21.(12分) 如图,在矩形ABCD中,AB=4,BC=3,AF平分∠DAC,分别交DC,BC的延长线于点E,F;连接DF,过点A作AH∥DF,分别交BD,BF于点G,H.
(1)求DE的长;
(2)求证:∠1=∠DFC.
22.(12分) 如图①,P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫作△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证: △ABP∽△BCP;
②若PA=3,PC=4,求PB的长;
(2)如图②,已知锐角△ABC,分别以AB,AC为边向外作正△ABE和正△ACD,CE和BD相交于点P,连接AP.
①求∠CPD的度数;
②求证:点P为△ABC的费马点.
参考答案
1-5CCDBC 6-10CCCAD
11.8
12.2
13.5.1m
14.6
15.2.5
16.1
17. 解:如图.
18.证明:∵AB∥EF,∴△DEF∽△DAB.∴=.又∵EF∥CD,∴△BEF∽△BCD.∴=.∴+=+==1.∴+=.
19.证明:(1)∵AC平分∠DAB,∴∠DAC=∠CAB,∵∠ADC=∠ACB=90°,∴△ADC∽△ACB,∴=,∴AC2=AB·AD.(2)∵E为AB的中点,∠ACB=90°,∴CE=BE=AE,∴∠EAC=∠ECA,∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE∥AD,∴△AFD∽△CFE.
20.解:设AB为x m,BC为y m,根据题意知,△ABC∽△DEC,有=①.△ABD∽△GFD,有=②.联立①②,得x=32.答:建筑物AB的高度为32 m
21.解:(1)∵矩形ABCD中,AD∥CF,∴∠DAF=∠AFC,∵AF平分∠DAC,∴∠DAF=∠CAF,∴∠FAC=∠AFC,∴AC=CF,∵AB=4,BC=3,∴AC===5,∴CF=5,∵AD∥CF,∴△ADE∽△FCE,∴=,设DE=x,则=,解得x=,∴DE=
(2)∵AD∥FH,AH∥DF,∴四边形ADFH是平行四边形,∴AD=FH=3,∴CH=2,BH=5,∵AD∥BH,∴△ADG∽△HBG,∴=,∴=,∴DG=,∵DE=,∴==,∴EG∥BC,∴∠1=∠AHC,又∵DF∥AH,∴∠AHC=∠DFC,∠1=∠DFC
22.(1)①证明:∵∠PAB+∠PBA=180°-∠APB=60°,∠PBC+∠PBA=∠ABC=60°,∴∠PAB=∠PBC.又∵∠APB=∠BPC=120°,∴△ABP∽△BCP.
②解:由①可知△ABP∽△BCP,∴=,∴PB2=PA·PC=12,∴PB=2.
(2)①解:如图,∵△ABE和△ACD是正三角形,∴AE=AB,AC=AD,∠EAB=∠5=60°.∵∠EAC=∠EAB+∠BAC,∠BAD=∠BAC+∠5,∴∠EAC=∠BAD,∴△ACE≌△ADB,∴∠1=∠2.∵∠3=∠4,∴∠CPD=∠5=60°.
②证明:由①可知∠1=∠2,∠3=∠4,∴△ADF∽△PCF,∴AF∶PF=DF∶CF,∴AF∶DF=PF∶CF.∵∠AFP=∠CFD,∴△AFP∽△DFC,∴∠APF=∠ACD=60°.由①可知∠CPD=60°,∴∠APC=∠CPD+∠APF=120°,∠BPC=180°-∠CPD=120°,∴∠APB=360°-∠BPC-∠APC=120°,∴点P为△ABC的费马点.
第二十七章 相似
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 在下列各组线段中,不成比例的是( )
A.a=3,b=6,c=2,d=4
B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=5,d=10
D.a=1,b=,c=,d=
2. 如图,在△ABC中,DE∥BC,=,则下列结论正确的是( )
A.= B.= C.= D.=
3. 如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,点O为位似中心,若OD=OD′,则A′B′∶AB为( )
A.2∶3 B.3∶2 C.1∶2 D.2∶1
4. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20 m,EC=10 m,CD=20 m,则河的宽度AB等于( )
A.60 m B.40 m C.30 m D.20 m
5. 如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E.若线段DE=5,则线段BC的长为( )
A.7.5 B.10 C.15 D.20
6. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5 cm,6 cm和9 cm,另一个三角形的最短边长为2.5 cm,则它的最长边为( )
A.3 cm B.4 cm C.4.5 cm D.5 cm
7. 如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
A.= B.= C.= D.=
8. 如图,在△ABC中,AB=7 cm,AC=4 cm,点D从B点以每秒2 cm的速度向点A移动,点E从A点以每秒1 cm的速度向点C移动,若D、E同时出发,同时停止且停止时△ADE与△ABC相似,则经过的时间是( )
A. s B. s C. s或 s D. s或 s
9.为了测量校园水平地面上一棵不可攀登的树的高度,学校数学兴趣小组做了如下探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子水平放置在离树8.4 m远的点E处,然后沿着直线BE走到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2 m,观察者眼高CD=1.6 m,则树AB的高度为( )
A.4.2 m B.4.8 m C.6.4 m D.16.8 m
10. 如图,AB是半圆O的直径,点C是的中点,点D是的中点,连接AC,BD交于点E,则等于( )
A. B. C.1- D.
二.填空题(共6小题,4*6=24)
11. 已知线段a,b,c,d成比例,且线段a=6,c=18,d=24,则b=__ __.
12. 如图,直线AD∥BE∥CF,BC=AC,DE=4,那么EF的值是________.
13. 如图,身高为1.7m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A、E、C′在一条线上.已知河BD的宽度为12m,BE=3m,则树CD的高为 .
14. 如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,CA′与AB的延长线相交于点D,则线段BD的长为__ __.
15.如图,有一个广告牌OE,小明站在距广告牌OE 10米远的A处恰好可以看到广告牌顶端,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则广告牌OE的高度为 米.
16.如图,四边形ABCD中,AD∥BC,CM是∠BCD的平分线,且CM⊥AB,M为垂足,AM=13AB.若四边形ABCD的面积为157,则四边形AMCD的面积是 .’
三.解答题(共5小题, 56分)
17.(6分) 如图,在直角坐标系中,△ABO三个顶点及点P的坐标分别是O(0,0),A(4,2),B(2,4),P(4,4),以点P为位似中心,画△DEF与△ABO位似,且相似比为1:2,请在直角坐标系中画出符合条件的△DEF.
18.(8分) 如图,AD与BC相交于E,点F在BD上,且AB∥EF∥CD,
求证:+=.
19.(8分) 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.求证:
(1)AC2=AB·AD;
(2)△AFD∽△CFE.
20.(10分) 如图,小明想测量河对岸建筑物AB的高度,在地面上C处放置了一块平面镜,然后从C点向后退了2.4米至D处,小明的眼睛E恰好看到了镜中建筑物A的像,在D处做好标记,将平面镜移至D处,小明再次从D点后退2.52米至F处,眼睛G恰好又看到了建筑物顶端A的像,已知小明眼睛距地面的高度ED,GF均为1.6米,求建筑物AB的高度.(注:图中的左侧α,β为入射角,右侧的α,β为反射角)
21.(12分) 如图,在矩形ABCD中,AB=4,BC=3,AF平分∠DAC,分别交DC,BC的延长线于点E,F;连接DF,过点A作AH∥DF,分别交BD,BF于点G,H.
(1)求DE的长;
(2)求证:∠1=∠DFC.
22.(12分) 如图①,P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫作△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证: △ABP∽△BCP;
②若PA=3,PC=4,求PB的长;
(2)如图②,已知锐角△ABC,分别以AB,AC为边向外作正△ABE和正△ACD,CE和BD相交于点P,连接AP.
①求∠CPD的度数;
②求证:点P为△ABC的费马点.
参考答案
1-5CCDBC 6-10CCCAD
11.8
12.2
13.5.1m
14.6
15.2.5
16.1
17. 解:如图.
18.证明:∵AB∥EF,∴△DEF∽△DAB.∴=.又∵EF∥CD,∴△BEF∽△BCD.∴=.∴+=+==1.∴+=.
19.证明:(1)∵AC平分∠DAB,∴∠DAC=∠CAB,∵∠ADC=∠ACB=90°,∴△ADC∽△ACB,∴=,∴AC2=AB·AD.(2)∵E为AB的中点,∠ACB=90°,∴CE=BE=AE,∴∠EAC=∠ECA,∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE∥AD,∴△AFD∽△CFE.
20.解:设AB为x m,BC为y m,根据题意知,△ABC∽△DEC,有=①.△ABD∽△GFD,有=②.联立①②,得x=32.答:建筑物AB的高度为32 m
21.解:(1)∵矩形ABCD中,AD∥CF,∴∠DAF=∠AFC,∵AF平分∠DAC,∴∠DAF=∠CAF,∴∠FAC=∠AFC,∴AC=CF,∵AB=4,BC=3,∴AC===5,∴CF=5,∵AD∥CF,∴△ADE∽△FCE,∴=,设DE=x,则=,解得x=,∴DE=
(2)∵AD∥FH,AH∥DF,∴四边形ADFH是平行四边形,∴AD=FH=3,∴CH=2,BH=5,∵AD∥BH,∴△ADG∽△HBG,∴=,∴=,∴DG=,∵DE=,∴==,∴EG∥BC,∴∠1=∠AHC,又∵DF∥AH,∴∠AHC=∠DFC,∠1=∠DFC
22.(1)①证明:∵∠PAB+∠PBA=180°-∠APB=60°,∠PBC+∠PBA=∠ABC=60°,∴∠PAB=∠PBC.又∵∠APB=∠BPC=120°,∴△ABP∽△BCP.
②解:由①可知△ABP∽△BCP,∴=,∴PB2=PA·PC=12,∴PB=2.
(2)①解:如图,∵△ABE和△ACD是正三角形,∴AE=AB,AC=AD,∠EAB=∠5=60°.∵∠EAC=∠EAB+∠BAC,∠BAD=∠BAC+∠5,∴∠EAC=∠BAD,∴△ACE≌△ADB,∴∠1=∠2.∵∠3=∠4,∴∠CPD=∠5=60°.
②证明:由①可知∠1=∠2,∠3=∠4,∴△ADF∽△PCF,∴AF∶PF=DF∶CF,∴AF∶DF=PF∶CF.∵∠AFP=∠CFD,∴△AFP∽△DFC,∴∠APF=∠ACD=60°.由①可知∠CPD=60°,∴∠APC=∠CPD+∠APF=120°,∠BPC=180°-∠CPD=120°,∴∠APB=360°-∠BPC-∠APC=120°,∴点P为△ABC的费马点.
