2022年人教版七年级数学下册5.1.2 垂线(第二课时)课件(26张)
文档属性
| 名称 | 2022年人教版七年级数学下册5.1.2 垂线(第二课时)课件(26张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 612.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
第五章 相交线与平行线
5.1.2 垂线
第二课时
【学习目标】
1.理解垂线段的概念、“垂线段最短”的性质;
2.理解点到直线的距离的意义并会度量点到直线的距离。
【课前预习】
1.已知A、B为平面上的2个定点,且AB=5.若点A、B到直线l的距离分别等于2、3,则满足条件的直线共有( )条.
A.2 B.3 C.4 D.5
2.点A、B、C为直线l上三点,点P为直线l外一点,且PA=3cm,PB=4cm,PC=5cm,则点P到直线l的距离为( )
A.2cm B.3cm C.小于3cm D.不大于3cm
3.下列说法:
①两点之间,直线最短;②若AC=BC,且A,B,C三点共线,则点C是线段AB的中点;③经过一点有且只有一条直线与已知直线垂直;④经过一点有且只有一条直线与已知直线平行.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法正确的是( )
A.两条直线被第三条直线所截,内错角相等B.垂直于同一条直线的两条直线互相垂直C.在平面内过一点有且只有一条直线与已知直线垂直D.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
5.下列说法中,正确的是( )
A.如果两个角相等,那么这两个角是对顶角B.连接直线外一点与直线上各点的所有线段中,垂线段最短C.如果两条直线被第三条直线所截,那么内错角相等D.经过一点有且只有一条直线与已知直线平行
【课前预习】答案
1.B
2.D
3.A
4.C
5.B
1、同一平面内,两条直线的位置关系:______.
2、怎样的两条直线我们称它们互相垂直?
3、一条直线仅有一条垂线.对吗?
复习回顾
过一点有且只有一条直线与已知直线垂直.
注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
垂线的性质(1):
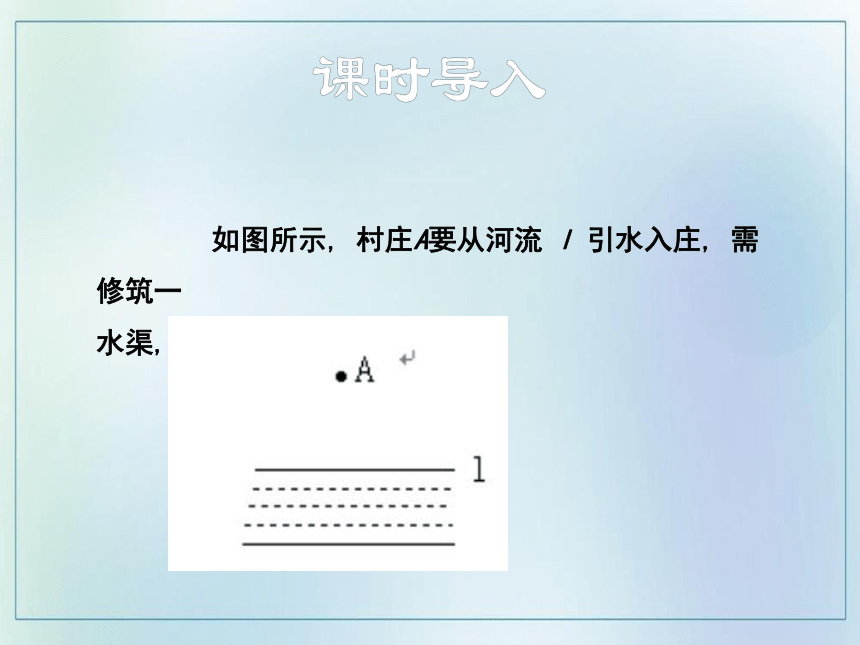
如图所示, 村庄A要从河流 l 引水入庄, 需修筑一
水渠, 如何修水渠最短呢?
上学期我们曾经学过什么最短的知识?
两点之间,线段最短。
一、垂线段的定义
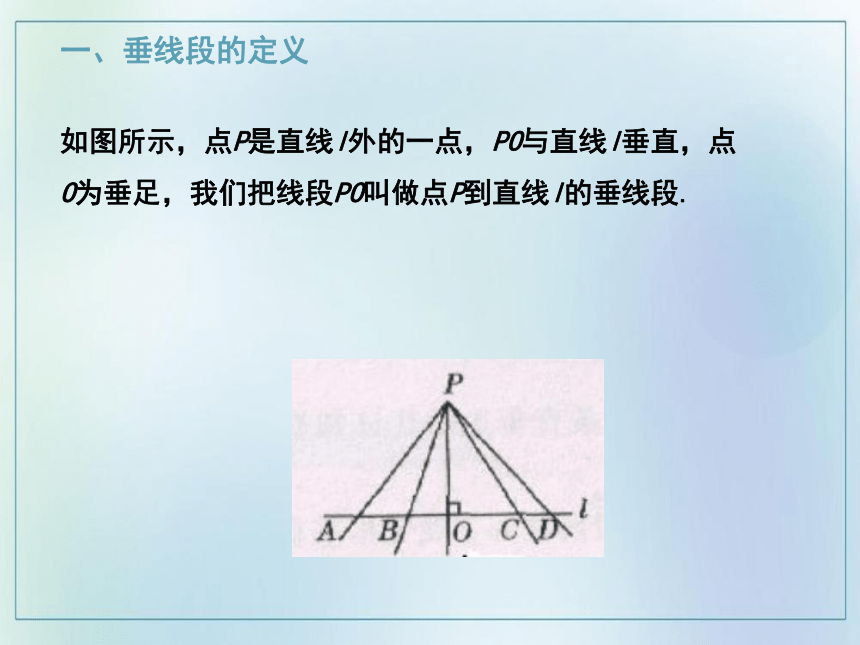
如图所示,点P是直线l外的一点,PO与直线l垂直,点O为垂足,我们把线段PO叫做点P到直线l的垂线段.
总 结
过直线外一点画已知直线的垂线,连接这点与垂足之间的线段,叫做这点到已知直线的垂线段.
如图所示,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中,正确的个数为( )
①AB与AC互相垂直;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AB;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到BC的距离.
A.2 B.3
C.4 D.5
例1
A
根据垂直定义,可知①正确,②错误;点C到AB
的垂线段应是线段AC,故③错误;点到直线的距
离是线段的长度而不是线段,故④⑥错误;⑤符
合定义,正确.
分析:
总 结
解答概念、性质辨析题,首先要熟记概念和性质,然后根据垂线的定义与性质、垂线段与点到直线
距离的概念作出正确的判断即可.所以记忆与理解相
结合是学好数学的前提.
二:垂线段的性质
连接直线外一点与直线上各点的所有线段中,垂线段最短。
垂线段最短
P
A
B
C
m
D
简单说成:垂线段最短.
垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足.
A
B
P
D
特别强调:
如图所示,AB是一条河流,要铺设管道将河水引
到C、D两个用水点,现有两种铺设管道的方案:
方案一:分别过点C,D作AB的垂线,垂足分别为点E,F,沿CE,DF铺设管道;
方案二:连接CD交AB于点P,
沿PC,PD铺设管道.
这两种铺设管道的方案哪一种
更节省材料?为什么?
(忽略河流的宽度)
例2
要尽可能节省材料,也就是让管道的总长度最
短.方案一中CE,DF是垂线段,而方案二中PC,
PD不是垂线段,所以CE<PC,DF<PD,所以
CE+DF<PC+PD,所以方案一更节省材料.
解:
导引:
按方案一铺设管道更节省材料,理由如下:
因为CE⊥AB,DF⊥AB,CD不垂直于AB,
根据“垂线段最短”可知,CE<PC,DF<DP,
所以CE+DF<PC+DP.
所以沿CE,DF铺设管道更节省材料.
总 结
本题主要利用“垂线段最短”来解决实际问题,解这类求最短距离问题时,要注意“垂线段最短”与“两点之间,线段最短”的区别,辨明这两条性质的应用条件:点到直线的距离,两点间的距离;正确运用解题方法.
三:点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
P
l
A
例如:如图,PA⊥l于点A ,垂线段PA的长度叫做点P到直线l的距离.
例:如图,是一个同学跳远的位置跳远成绩怎么表示
l
P
A
解:过P点作PA⊥l于点A ,垂线段PA的长度就是该同学的跳远成绩.
例4 如图,在三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=4 cm,BC=3 cm,AB=5 cm,则点A到直线BC的距离为______cm,点B到直线AC的距离为______cm,点C到直线AB的距离为______cm.
4
3
2.4
导引:根据点到直线的距离的定义可知,点A到直线BC
的距离是线段AC的长,点B到直线AC的距离是线段BC的长,点C到直线AB的距离是线段CD的长.
因为三角形ABC的面积S=
所以AC·BC=AB·CD,进而可得CD=2.4 cm.
总 结
正确理解点到直线的距离及两点间的距离是解决此类问题的关键.解决此类问题应注意:(1)点到直线的距离是点到直线的垂线段的长度,而不是垂线,也不是垂线段;(2)距离表示线段的长度,是一个数量,与线段不能等同;(3)用垂线段的长度表示点到直线的距离,其实质是点与垂足两点间的距离,体现了数形结合思想.
垂线段是一条与已知直线垂直的线段. 垂线段所
在的直线是已知直线的垂线;垂线段所在的直线与已知直线垂直.
点到直线的距离:直线外一点到这条直线的垂线
段的长度,叫做点到直线的距离.
课堂小结
【课后练习】
1.下列说法不正确的是( )
A.对顶角相等 B.两点确定一条直线C.一个角的补角一定大于这个角D.垂线段最短
2.下列说法中,正确的是( )
A.在同一平面内,过一点有无数条直线与已知直线垂直B.两直线相交,对顶角互补C.垂线段最短D.直线外一点到这条直线的垂线段叫做点到直线的距离
3.下列四个说法:①两点之间,线段最短;②连接两点之间的线段叫做这两点间的距离;③经过直线外一点,有且只有一条直线与这条直线平行;④直线外一点与这条直线上各点连接的所有线段中,垂线段最短.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
4.下列选项中,不是运用“垂线段最短”这一性质的是( )
A.立定跳远时测量落点后端到起跳线的距离 B.从一个村庄向一条河引一条最短的水渠
C.把弯曲的公路改成直道可以缩短路程 D.直角三角形中任意一条直角边的长度都比斜边短
5.已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离为( )
A.4 cm B.5 cm C.小于2 cm D.不大于2 cm
6.A是直线a外一点,B是直线a上一点,A到a的距离为3 cm,那么AB__________3 cm.
7.定点P在直线AB外,动点O在直线AB上移动,当PO最短时,∠POA=_______;这时线段PO所在的直线是直线AB的________,线段PO叫做直线AB的__________.
8.已知△ABC的面积是12平方厘米,BC的长是8厘米,那么点A到线段BC的距离是_______厘米.
9.直线l1与l2相交于点O,对于平面内任意一点M,若点M到直线l1的距离为1,且到直线l2的距离为2,则符合条件的点M的个数是______ .
10.直线外一点到这条直线的垂线段的长度,叫做__________.
【课后练习】答案
1.C 2.C 3.C 4.C 5.D
6.≥
7.90° 垂线 垂线段
8.3
9.4
10.点到直线的距离
第五章 相交线与平行线
5.1.2 垂线
第二课时
【学习目标】
1.理解垂线段的概念、“垂线段最短”的性质;
2.理解点到直线的距离的意义并会度量点到直线的距离。
【课前预习】
1.已知A、B为平面上的2个定点,且AB=5.若点A、B到直线l的距离分别等于2、3,则满足条件的直线共有( )条.
A.2 B.3 C.4 D.5
2.点A、B、C为直线l上三点,点P为直线l外一点,且PA=3cm,PB=4cm,PC=5cm,则点P到直线l的距离为( )
A.2cm B.3cm C.小于3cm D.不大于3cm
3.下列说法:
①两点之间,直线最短;②若AC=BC,且A,B,C三点共线,则点C是线段AB的中点;③经过一点有且只有一条直线与已知直线垂直;④经过一点有且只有一条直线与已知直线平行.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法正确的是( )
A.两条直线被第三条直线所截,内错角相等B.垂直于同一条直线的两条直线互相垂直C.在平面内过一点有且只有一条直线与已知直线垂直D.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
5.下列说法中,正确的是( )
A.如果两个角相等,那么这两个角是对顶角B.连接直线外一点与直线上各点的所有线段中,垂线段最短C.如果两条直线被第三条直线所截,那么内错角相等D.经过一点有且只有一条直线与已知直线平行
【课前预习】答案
1.B
2.D
3.A
4.C
5.B
1、同一平面内,两条直线的位置关系:______.
2、怎样的两条直线我们称它们互相垂直?
3、一条直线仅有一条垂线.对吗?
复习回顾
过一点有且只有一条直线与已知直线垂直.
注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
垂线的性质(1):
如图所示, 村庄A要从河流 l 引水入庄, 需修筑一
水渠, 如何修水渠最短呢?
上学期我们曾经学过什么最短的知识?
两点之间,线段最短。
一、垂线段的定义
如图所示,点P是直线l外的一点,PO与直线l垂直,点O为垂足,我们把线段PO叫做点P到直线l的垂线段.
总 结
过直线外一点画已知直线的垂线,连接这点与垂足之间的线段,叫做这点到已知直线的垂线段.
如图所示,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中,正确的个数为( )
①AB与AC互相垂直;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AB;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到BC的距离.
A.2 B.3
C.4 D.5
例1
A
根据垂直定义,可知①正确,②错误;点C到AB
的垂线段应是线段AC,故③错误;点到直线的距
离是线段的长度而不是线段,故④⑥错误;⑤符
合定义,正确.
分析:
总 结
解答概念、性质辨析题,首先要熟记概念和性质,然后根据垂线的定义与性质、垂线段与点到直线
距离的概念作出正确的判断即可.所以记忆与理解相
结合是学好数学的前提.
二:垂线段的性质
连接直线外一点与直线上各点的所有线段中,垂线段最短。
垂线段最短
P
A
B
C
m
D
简单说成:垂线段最短.
垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足.
A
B
P
D
特别强调:
如图所示,AB是一条河流,要铺设管道将河水引
到C、D两个用水点,现有两种铺设管道的方案:
方案一:分别过点C,D作AB的垂线,垂足分别为点E,F,沿CE,DF铺设管道;
方案二:连接CD交AB于点P,
沿PC,PD铺设管道.
这两种铺设管道的方案哪一种
更节省材料?为什么?
(忽略河流的宽度)
例2
要尽可能节省材料,也就是让管道的总长度最
短.方案一中CE,DF是垂线段,而方案二中PC,
PD不是垂线段,所以CE<PC,DF<PD,所以
CE+DF<PC+PD,所以方案一更节省材料.
解:
导引:
按方案一铺设管道更节省材料,理由如下:
因为CE⊥AB,DF⊥AB,CD不垂直于AB,
根据“垂线段最短”可知,CE<PC,DF<DP,
所以CE+DF<PC+DP.
所以沿CE,DF铺设管道更节省材料.
总 结
本题主要利用“垂线段最短”来解决实际问题,解这类求最短距离问题时,要注意“垂线段最短”与“两点之间,线段最短”的区别,辨明这两条性质的应用条件:点到直线的距离,两点间的距离;正确运用解题方法.
三:点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
P
l
A
例如:如图,PA⊥l于点A ,垂线段PA的长度叫做点P到直线l的距离.
例:如图,是一个同学跳远的位置跳远成绩怎么表示
l
P
A
解:过P点作PA⊥l于点A ,垂线段PA的长度就是该同学的跳远成绩.
例4 如图,在三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=4 cm,BC=3 cm,AB=5 cm,则点A到直线BC的距离为______cm,点B到直线AC的距离为______cm,点C到直线AB的距离为______cm.
4
3
2.4
导引:根据点到直线的距离的定义可知,点A到直线BC
的距离是线段AC的长,点B到直线AC的距离是线段BC的长,点C到直线AB的距离是线段CD的长.
因为三角形ABC的面积S=
所以AC·BC=AB·CD,进而可得CD=2.4 cm.
总 结
正确理解点到直线的距离及两点间的距离是解决此类问题的关键.解决此类问题应注意:(1)点到直线的距离是点到直线的垂线段的长度,而不是垂线,也不是垂线段;(2)距离表示线段的长度,是一个数量,与线段不能等同;(3)用垂线段的长度表示点到直线的距离,其实质是点与垂足两点间的距离,体现了数形结合思想.
垂线段是一条与已知直线垂直的线段. 垂线段所
在的直线是已知直线的垂线;垂线段所在的直线与已知直线垂直.
点到直线的距离:直线外一点到这条直线的垂线
段的长度,叫做点到直线的距离.
课堂小结
【课后练习】
1.下列说法不正确的是( )
A.对顶角相等 B.两点确定一条直线C.一个角的补角一定大于这个角D.垂线段最短
2.下列说法中,正确的是( )
A.在同一平面内,过一点有无数条直线与已知直线垂直B.两直线相交,对顶角互补C.垂线段最短D.直线外一点到这条直线的垂线段叫做点到直线的距离
3.下列四个说法:①两点之间,线段最短;②连接两点之间的线段叫做这两点间的距离;③经过直线外一点,有且只有一条直线与这条直线平行;④直线外一点与这条直线上各点连接的所有线段中,垂线段最短.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
4.下列选项中,不是运用“垂线段最短”这一性质的是( )
A.立定跳远时测量落点后端到起跳线的距离 B.从一个村庄向一条河引一条最短的水渠
C.把弯曲的公路改成直道可以缩短路程 D.直角三角形中任意一条直角边的长度都比斜边短
5.已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离为( )
A.4 cm B.5 cm C.小于2 cm D.不大于2 cm
6.A是直线a外一点,B是直线a上一点,A到a的距离为3 cm,那么AB__________3 cm.
7.定点P在直线AB外,动点O在直线AB上移动,当PO最短时,∠POA=_______;这时线段PO所在的直线是直线AB的________,线段PO叫做直线AB的__________.
8.已知△ABC的面积是12平方厘米,BC的长是8厘米,那么点A到线段BC的距离是_______厘米.
9.直线l1与l2相交于点O,对于平面内任意一点M,若点M到直线l1的距离为1,且到直线l2的距离为2,则符合条件的点M的个数是______ .
10.直线外一点到这条直线的垂线段的长度,叫做__________.
【课后练习】答案
1.C 2.C 3.C 4.C 5.D
6.≥
7.90° 垂线 垂线段
8.3
9.4
10.点到直线的距离
