5.4 平移 课件(共24张PPT)
图片预览



文档简介
(共24张PPT)
人教版数学 七年级下册
第五章 相交线与平行线
5.4 平移
课堂小结
例题讲解
随堂演练
获取新知
情景导入
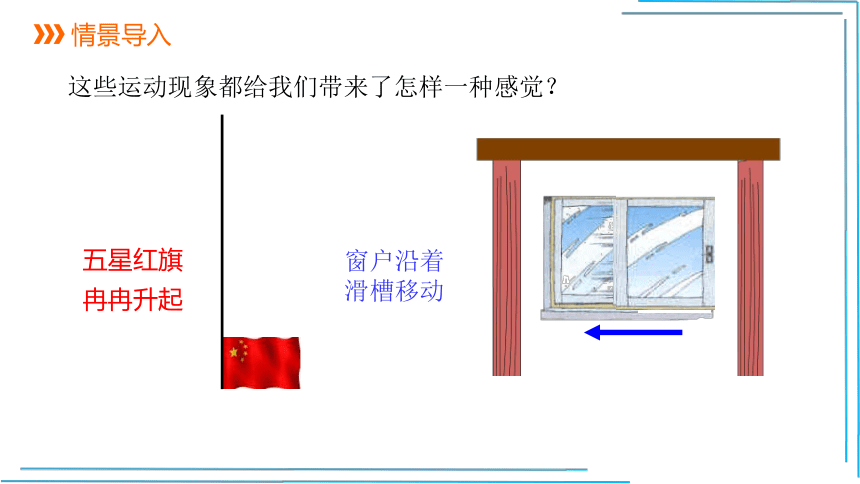
情景导入
五星红旗冉冉升起
这些运动现象都给我们带来了怎样一种感觉?
窗户沿着滑槽移动
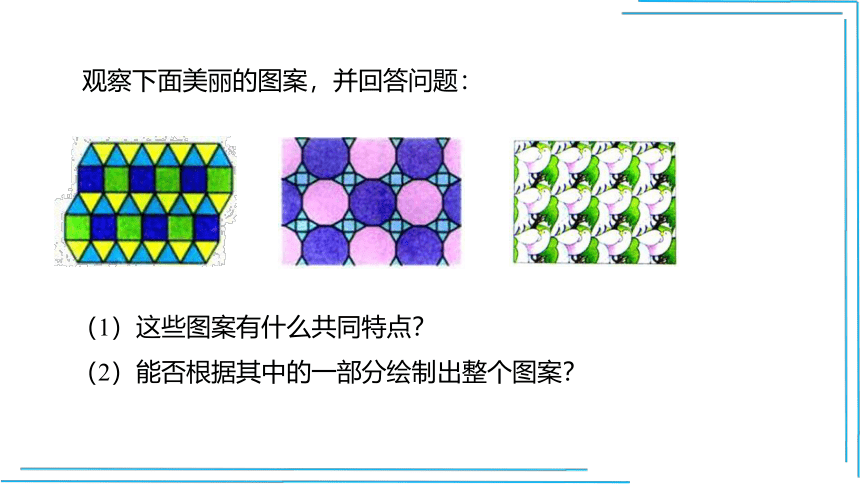
观察下面美丽的图案,并回答问题:
(1)这些图案有什么共同特点?
(2)能否根据其中的一部分绘制出整个图案?
探究:如何在一张半透明的纸上,画出一排形状和大小如图所示的雪人呢
获取新知
知识点一:平移的概念
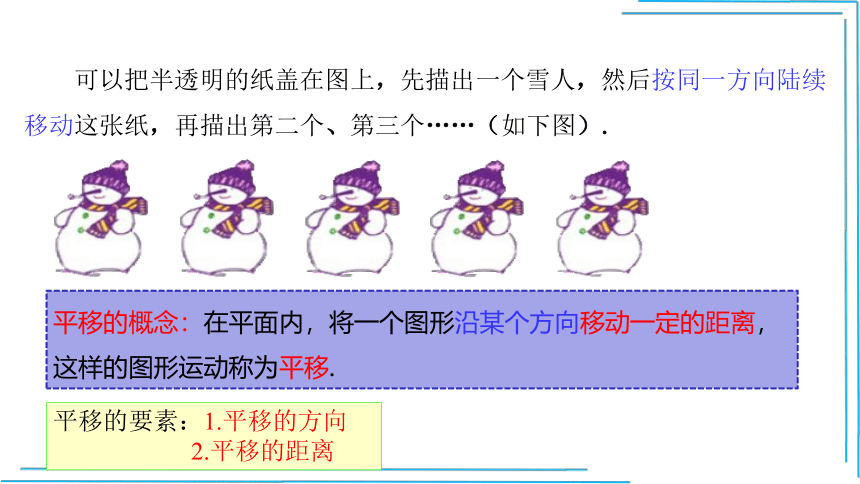
可以把半透明的纸盖在图上,先描出一个雪人,然后按同一方向陆续
移动这张纸,再描出第二个、第三个……(如下图).
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
平移的要素:1.平移的方向
2.平移的距离
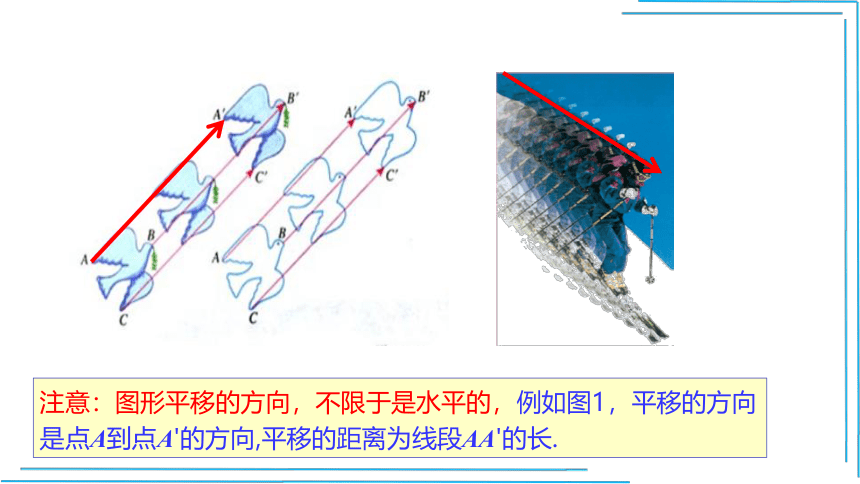
注意:图形平移的方向,不限于是水平的,例如图1,平移的方向是点A到点A'的方向,平移的距离为线段AA'的长.
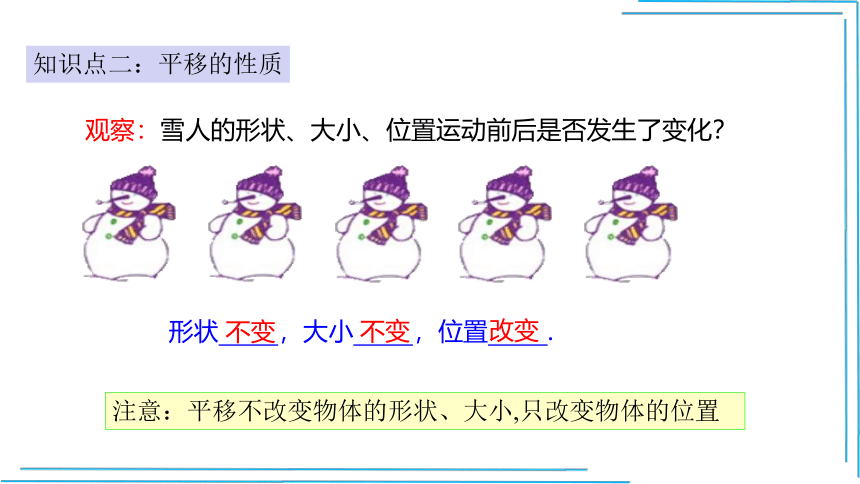
知识点二:平移的性质
观察:雪人的形状、大小、位置运动前后是否发生了变化?
形状 ,大小 ,位置 .
不变
不变
改变
注意:平移不改变物体的形状、大小,只改变物体的位置
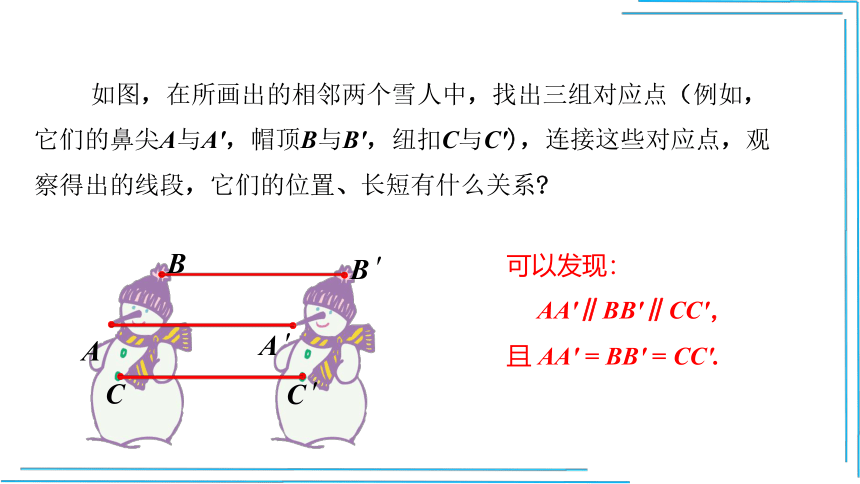
如图,在所画出的相邻两个雪人中,找出三组对应点(例如,它们的鼻尖A与A',帽顶B与B',纽扣C与C'),连接这些对应点,观察得出的线段,它们的位置、长短有什么关系
A
A
'
C
C
'
B
B
'
可以发现:
AA′∥BB′∥CC′,
且 AA′ = BB′ = CC′.
平移的性质:
1.把一个图形整体沿着某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
2. 新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行(或在同一条直线上)且相等.
如图,平移三角形ABC,使点A移动到点A',
画出平移后的三角形A'B'C'.
A
B
C
A
知识点三:平移作图
分析:图形平移后的对应点有什么特征 作出点B和点C的对应点B',C',能确定△A'B'C'吗?
过点C作AA'的平行线l1,在l1上截取CC'=AA',
则点C'就是点C 的对应点.
顺次连接A’,B’,C',得到平移后的三角形A'B'C' .
解:如图,连接AA',
过点B作AA'的平行线l,在l上截取BB'=AA',
则点B'就是点B的对应点.
A
B
C
A
B
l
C
平移作图的一般步骤:
应分四步——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图顺次连接对应点.
例题讲解
例1 以下现象:
①打开教室的门时,门的移动;
②打气筒打气时,活塞的运动;
③钟摆的摆动;
④传送带上,瓶装饮料的移动,其中属于平移的是( )
A.①② B.①③
C.②③ D.②④
D
例2 如图,图形中有两个梯形ABCD和EFGH,其中梯形EFGH是由梯形ABCD向右平移2 cm后得到的,问:
(1)线段AE,BF,CG,DH之间有什么数量关系?
(2)AB与EF,BC与FG,CD与GH,AD与EH之间有什么关系?
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE之间有什么数量关系?
解:(1)线段AE,BF,CG,DH的长度相等,都为2 cm.
(2)AB与EF,BC与FG,CD与GH,AD与EH分别平行且相等.
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE对应相等.
随堂演练
1.下列生活中的物体的运动情况可以看成平移的是( )
A.篮球运动员投篮时篮球的运动
B.飞机在跑道上滑行到停止的运动
C.空中放飞的风筝的运动
D.冷水加热过程中小气泡上升变为大气泡
B
2. 将如图所示的图案平移后,可以得到的图案是( )
A
4. 如图,将三角形ABC 沿直线AB向右平移后到达三角形BDE的位置.若∠CAB=50°, 则∠EBD的度数为 .
50°
4.下列图案可以由什么图形平移形成?
解:如图
5.如图,经过平移,四边形ABCD的顶点A移动到点A′,
作出平移后的四边形.
A
B
C
D
A′
D′
C′
B′
解:如图所示,
四边形A′B′C′D′
为所求.
课堂小结
定--找--移--连
平移前后图形的形状和大小,完全相同
对应线段平行(或在同一直线上)且相等,
对应角相等
各对应点所连线段平行(或在同一直线上)且相等
平移
平移的要素
平移的性质
平移作图
平移的方向和距离
https://www.21cnjy.com/help/help_extract.php
人教版数学 七年级下册
第五章 相交线与平行线
5.4 平移
课堂小结
例题讲解
随堂演练
获取新知
情景导入
情景导入
五星红旗冉冉升起
这些运动现象都给我们带来了怎样一种感觉?
窗户沿着滑槽移动
观察下面美丽的图案,并回答问题:
(1)这些图案有什么共同特点?
(2)能否根据其中的一部分绘制出整个图案?
探究:如何在一张半透明的纸上,画出一排形状和大小如图所示的雪人呢
获取新知
知识点一:平移的概念
可以把半透明的纸盖在图上,先描出一个雪人,然后按同一方向陆续
移动这张纸,再描出第二个、第三个……(如下图).
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
平移的要素:1.平移的方向
2.平移的距离
注意:图形平移的方向,不限于是水平的,例如图1,平移的方向是点A到点A'的方向,平移的距离为线段AA'的长.
知识点二:平移的性质
观察:雪人的形状、大小、位置运动前后是否发生了变化?
形状 ,大小 ,位置 .
不变
不变
改变
注意:平移不改变物体的形状、大小,只改变物体的位置
如图,在所画出的相邻两个雪人中,找出三组对应点(例如,它们的鼻尖A与A',帽顶B与B',纽扣C与C'),连接这些对应点,观察得出的线段,它们的位置、长短有什么关系
A
A
'
C
C
'
B
B
'
可以发现:
AA′∥BB′∥CC′,
且 AA′ = BB′ = CC′.
平移的性质:
1.把一个图形整体沿着某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
2. 新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行(或在同一条直线上)且相等.
如图,平移三角形ABC,使点A移动到点A',
画出平移后的三角形A'B'C'.
A
B
C
A
知识点三:平移作图
分析:图形平移后的对应点有什么特征 作出点B和点C的对应点B',C',能确定△A'B'C'吗?
过点C作AA'的平行线l1,在l1上截取CC'=AA',
则点C'就是点C 的对应点.
顺次连接A’,B’,C',得到平移后的三角形A'B'C' .
解:如图,连接AA',
过点B作AA'的平行线l,在l上截取BB'=AA',
则点B'就是点B的对应点.
A
B
C
A
B
l
C
平移作图的一般步骤:
应分四步——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图顺次连接对应点.
例题讲解
例1 以下现象:
①打开教室的门时,门的移动;
②打气筒打气时,活塞的运动;
③钟摆的摆动;
④传送带上,瓶装饮料的移动,其中属于平移的是( )
A.①② B.①③
C.②③ D.②④
D
例2 如图,图形中有两个梯形ABCD和EFGH,其中梯形EFGH是由梯形ABCD向右平移2 cm后得到的,问:
(1)线段AE,BF,CG,DH之间有什么数量关系?
(2)AB与EF,BC与FG,CD与GH,AD与EH之间有什么关系?
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE之间有什么数量关系?
解:(1)线段AE,BF,CG,DH的长度相等,都为2 cm.
(2)AB与EF,BC与FG,CD与GH,AD与EH分别平行且相等.
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE对应相等.
随堂演练
1.下列生活中的物体的运动情况可以看成平移的是( )
A.篮球运动员投篮时篮球的运动
B.飞机在跑道上滑行到停止的运动
C.空中放飞的风筝的运动
D.冷水加热过程中小气泡上升变为大气泡
B
2. 将如图所示的图案平移后,可以得到的图案是( )
A
4. 如图,将三角形ABC 沿直线AB向右平移后到达三角形BDE的位置.若∠CAB=50°, 则∠EBD的度数为 .
50°
4.下列图案可以由什么图形平移形成?
解:如图
5.如图,经过平移,四边形ABCD的顶点A移动到点A′,
作出平移后的四边形.
A
B
C
D
A′
D′
C′
B′
解:如图所示,
四边形A′B′C′D′
为所求.
课堂小结
定--找--移--连
平移前后图形的形状和大小,完全相同
对应线段平行(或在同一直线上)且相等,
对应角相等
各对应点所连线段平行(或在同一直线上)且相等
平移
平移的要素
平移的性质
平移作图
平移的方向和距离
https://www.21cnjy.com/help/help_extract.php
