3.3垂径定理(课件)(共28张PPT)
文档属性
| 名称 | 3.3垂径定理(课件)(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 20:20:21 | ||
图片预览





文档简介
(共28张PPT)
北师大版九年级下册数学
第三章 圆
3.3 垂径定理
问题:左图中 AB 为圆 O 的直径,CD为圆 O 的弦,相交于点 E,当弦 CD 在圆上运动的过程中有没有特殊情况?
直径 AB 和弦 CD 互相垂直.
观察讨论
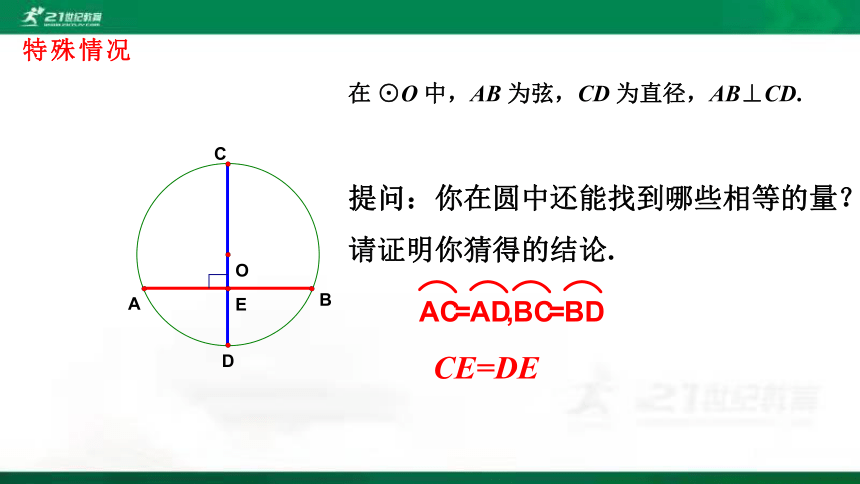
特殊情况
在 ⊙O 中,AB 为弦,CD 为直径,AB⊥CD.
提问:你在圆中还能找到哪些相等的量?请证明你猜得的结论.
CE=DE
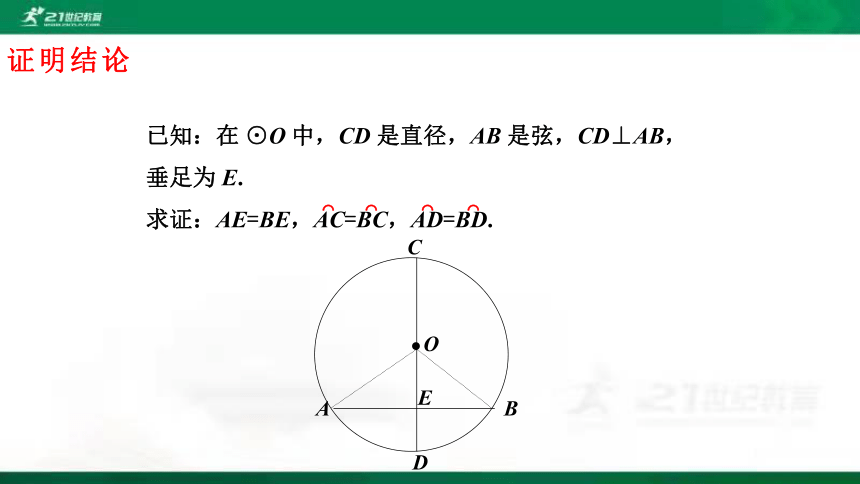
证明结论
已知:在 ⊙O 中,CD 是直径,AB 是弦,CD⊥AB,垂足为 E.
求证:AE=BE,AC=BC,AD=BD.
⌒
⌒
⌒
⌒
C
.
O
A
E
B
D
证明:连接 OA,OB,则 OA=OB.
因为垂直于弦 AB 的直径 CD 所在的直线既是等腰三角形 OAB 的对称轴,又是 ⊙O 的对称轴,
所以当把圆沿着直径 CD 折叠时,CD 两侧的两个半圆重合,点 A 与点 B 重合,AE 与 BE 重合,AC,AD 分别与 BC,BD 重合.
因此,AE=BE,AC=BC,AD=BD.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
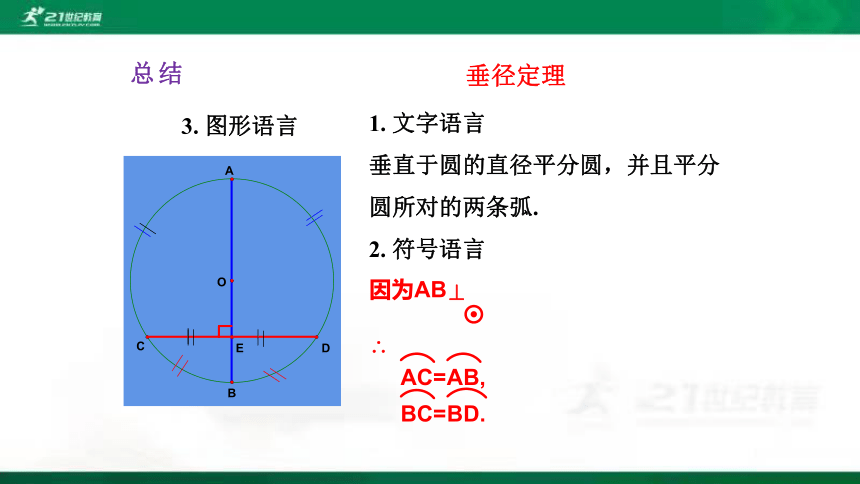
垂径定理
1. 文字语言
垂直于圆的直径平分圆,并且平分 圆所对的两条弧.
2. 符号语言
总结
3. 图形语言
2. 请画图说明垂径定理的条件和结论.
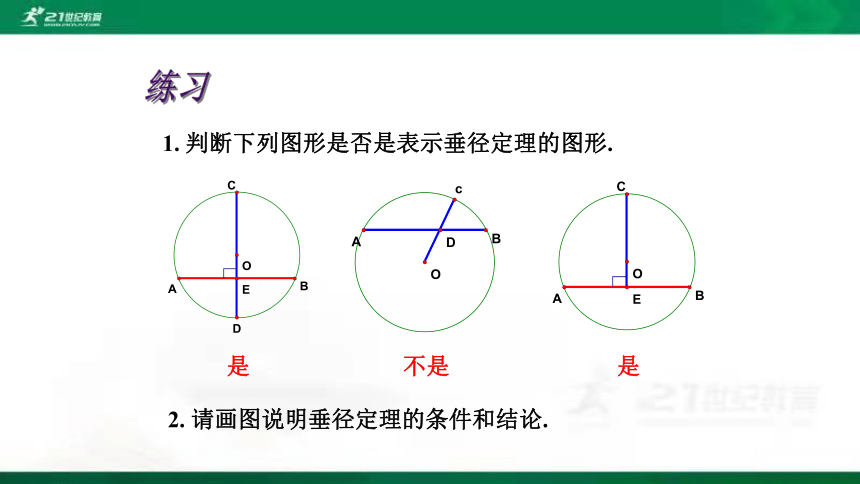
1. 判断下列图形是否是表示垂径定理的图形.
是
不是
是
练习
条件
结论
(1)过圆心;
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
分析
CD为直径,
CD⊥AB
}
{
点 C 平分弧 ACB
点 D 平分弧 ADB
CD 平分弦 AB
例 1 如图,已知在 ⊙O 中,弦 AB 的长为 8 cm,圆心 O 到 AB 的距离为 3 cm,求 ⊙O 的半径.
.
A
E
B
O
例题
解:连接 OA,过点 O 作 OE⊥AB,垂足为 E,
则 OE=3 cm,AE=BE.
∵AB=8 cm,∴AE=4 cm.
在 Rt△AOE 中,根据勾股定理,
得 OA=5 cm.
∴⊙O 的半径为 5 cm.
例 2 已知:如图,在以 O 为圆心的两个同心圆中,大圆的弦 AB 交小圆于 C,D 两点.
求证:AC=BD.
E
.
A
C
D
B
O
┐
证明:过点 O 作 OE⊥AB,垂足为 E,
则 AE=BE,CE=DE,
所以AE-CE=BE-DE,
即 AC=BD.
例 3 已知:⊙O 中弦 AB∥CD.
求证:AC=BD.
.
M
C
D
A
B
O
N
⌒
⌒
证明:作直径 MN⊥AB.
∵AB∥CD,∴MN⊥CD.
∴AM=BM,CM=DM(垂直平分弦的直径平分弦所对的弧),
∴ AM-CM=BM-DM,
即 AC=BD.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
垂径定理的几个基本图形
例1.如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上.你认为AC与BD的大小有什么关系?为什么?
G
└
解:作OG⊥AB,
∵AG=BG,CG=DG,
∴AC=BD.
例2.如图,一条公路的转弯处是一段圆弧(即图中 ,点
O是 所在圆的圆心),其中CD=600m,E是 上一点,且
OE⊥CD,垂足为F,EF=90m,求这段弯路的半径.
└
解:连接OC.
1.判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两
条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对
的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦. ( )
(4)弦的垂直平分线一定平分这条弦所对的弧( )
对
错
错
对
【跟踪训练】
●O
●M
2.如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
解:连接OM,过M作AB⊥OM,
交⊙O于A,B两点.
A
B
1.(上海·中考)如图,AB,AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,如果MN=3,那么BC=________.
【解析】由垂径定理得AN=CN,AM=BM,所以BC=2MN=6.
答案:6
2.(芜湖·中考)如图所示,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
A.19 B.16 C.18 D.20
答案:D
3.(烟台·中考)如图,△ ABC内接于⊙O,D为线段AB的
中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论
①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤
正确结论的个数是( )
A.2个 B.3个 C.4个 D.5个
答案:B
4.(湖州·中考)如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )
A.AE=OE B.CE=DE
C.OE= CE D.∠AOC=60°
.
答案:B
5.(襄阳·中考)如图,AB是⊙O的弦,半径OC⊥AB于D点,且AB=6cm,OD=4cm,则DC的长为( )
A.5cm B.2.5cm C.2cm D.1cm
答案:D
6.(襄阳·中考)已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
A.17cm B.7 cm
C.12 cm D.17 cm或7 cm
图(1) 图(2)
答案:D
【规律方法】运用垂径定理及其推论解决一些数学问题.最常见的辅助线是连接圆上的点与圆心构成半径,及过圆心作弦的垂线,构造直角三角形,利用勾股定理解决问题.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版九年级下册数学
第三章 圆
3.3 垂径定理
问题:左图中 AB 为圆 O 的直径,CD为圆 O 的弦,相交于点 E,当弦 CD 在圆上运动的过程中有没有特殊情况?
直径 AB 和弦 CD 互相垂直.
观察讨论
特殊情况
在 ⊙O 中,AB 为弦,CD 为直径,AB⊥CD.
提问:你在圆中还能找到哪些相等的量?请证明你猜得的结论.
CE=DE
证明结论
已知:在 ⊙O 中,CD 是直径,AB 是弦,CD⊥AB,垂足为 E.
求证:AE=BE,AC=BC,AD=BD.
⌒
⌒
⌒
⌒
C
.
O
A
E
B
D
证明:连接 OA,OB,则 OA=OB.
因为垂直于弦 AB 的直径 CD 所在的直线既是等腰三角形 OAB 的对称轴,又是 ⊙O 的对称轴,
所以当把圆沿着直径 CD 折叠时,CD 两侧的两个半圆重合,点 A 与点 B 重合,AE 与 BE 重合,AC,AD 分别与 BC,BD 重合.
因此,AE=BE,AC=BC,AD=BD.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
垂径定理
1. 文字语言
垂直于圆的直径平分圆,并且平分 圆所对的两条弧.
2. 符号语言
总结
3. 图形语言
2. 请画图说明垂径定理的条件和结论.
1. 判断下列图形是否是表示垂径定理的图形.
是
不是
是
练习
条件
结论
(1)过圆心;
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
分析
CD为直径,
CD⊥AB
}
{
点 C 平分弧 ACB
点 D 平分弧 ADB
CD 平分弦 AB
例 1 如图,已知在 ⊙O 中,弦 AB 的长为 8 cm,圆心 O 到 AB 的距离为 3 cm,求 ⊙O 的半径.
.
A
E
B
O
例题
解:连接 OA,过点 O 作 OE⊥AB,垂足为 E,
则 OE=3 cm,AE=BE.
∵AB=8 cm,∴AE=4 cm.
在 Rt△AOE 中,根据勾股定理,
得 OA=5 cm.
∴⊙O 的半径为 5 cm.
例 2 已知:如图,在以 O 为圆心的两个同心圆中,大圆的弦 AB 交小圆于 C,D 两点.
求证:AC=BD.
E
.
A
C
D
B
O
┐
证明:过点 O 作 OE⊥AB,垂足为 E,
则 AE=BE,CE=DE,
所以AE-CE=BE-DE,
即 AC=BD.
例 3 已知:⊙O 中弦 AB∥CD.
求证:AC=BD.
.
M
C
D
A
B
O
N
⌒
⌒
证明:作直径 MN⊥AB.
∵AB∥CD,∴MN⊥CD.
∴AM=BM,CM=DM(垂直平分弦的直径平分弦所对的弧),
∴ AM-CM=BM-DM,
即 AC=BD.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
垂径定理的几个基本图形
例1.如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上.你认为AC与BD的大小有什么关系?为什么?
G
└
解:作OG⊥AB,
∵AG=BG,CG=DG,
∴AC=BD.
例2.如图,一条公路的转弯处是一段圆弧(即图中 ,点
O是 所在圆的圆心),其中CD=600m,E是 上一点,且
OE⊥CD,垂足为F,EF=90m,求这段弯路的半径.
└
解:连接OC.
1.判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两
条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对
的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦. ( )
(4)弦的垂直平分线一定平分这条弦所对的弧( )
对
错
错
对
【跟踪训练】
●O
●M
2.如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
解:连接OM,过M作AB⊥OM,
交⊙O于A,B两点.
A
B
1.(上海·中考)如图,AB,AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,如果MN=3,那么BC=________.
【解析】由垂径定理得AN=CN,AM=BM,所以BC=2MN=6.
答案:6
2.(芜湖·中考)如图所示,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
A.19 B.16 C.18 D.20
答案:D
3.(烟台·中考)如图,△ ABC内接于⊙O,D为线段AB的
中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论
①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤
正确结论的个数是( )
A.2个 B.3个 C.4个 D.5个
答案:B
4.(湖州·中考)如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )
A.AE=OE B.CE=DE
C.OE= CE D.∠AOC=60°
.
答案:B
5.(襄阳·中考)如图,AB是⊙O的弦,半径OC⊥AB于D点,且AB=6cm,OD=4cm,则DC的长为( )
A.5cm B.2.5cm C.2cm D.1cm
答案:D
6.(襄阳·中考)已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
A.17cm B.7 cm
C.12 cm D.17 cm或7 cm
图(1) 图(2)
答案:D
【规律方法】运用垂径定理及其推论解决一些数学问题.最常见的辅助线是连接圆上的点与圆心构成半径,及过圆心作弦的垂线,构造直角三角形,利用勾股定理解决问题.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
