3.2圆的对称性 课件(共23张PPT)
文档属性
| 名称 | 3.2圆的对称性 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 675.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 20:22:42 | ||
图片预览






文档简介
(共23张PPT)
北师大版九年级下册数学
第三章 圆
3.2圆的对称性
情景导入
基础回顾
1. 什么是轴对称图形?我们以前学过哪些轴对称图形?
如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形.例如,线段、角、等腰三角形、矩形、菱形、等腰梯形、正方形.
2.我们所学的圆是不是轴对称图形呢?
.
圆是轴对称图形吗?如果是,它的对称轴是什么?你
能找到多少条对称轴?
你是用什么方法解决上述问题的
圆是中心对称图形吗?如果是,它的对称中心是什么?你能找到多少个对称中心?
你又是用什么方法解决这个问题的
圆是轴对称图形. 圆的对称轴是任意一条经过圆心的
直线,它有无数条对称轴.
●O
利用折叠的方法即可解决上述问题.
圆也是中心对称图形. 它的对称中
心就是圆心.
用旋转的方法即可解决这个问题.
这是圆特有的一个性质:圆的旋转不变性.
圆的对称性及特性
讲授新课
圆心角:顶点在圆心的角.
弦心距:过圆心作弦的垂线,圆心与垂足之间
的距离.
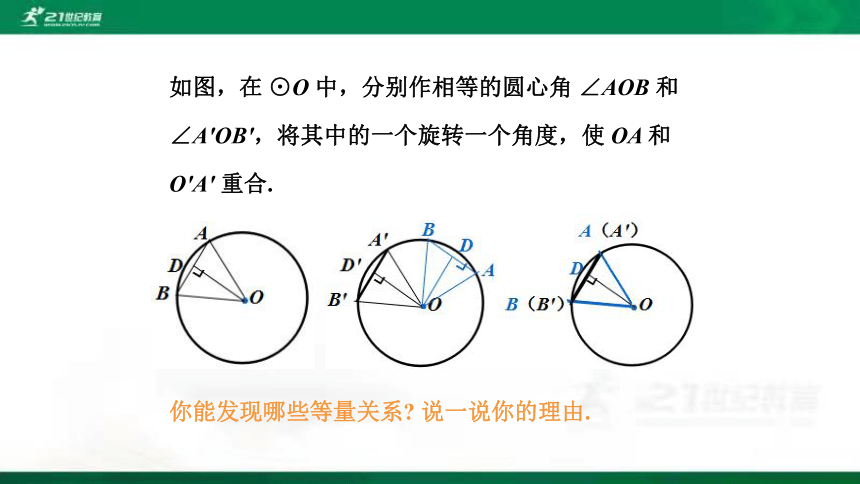
如图,在 ⊙O 中,分别作相等的圆心角 ∠AOB 和
∠A′OB′,将其中的一个旋转一个角度,使 OA 和
O′A′ 重合.
你能发现哪些等量关系 说一说你的理由.
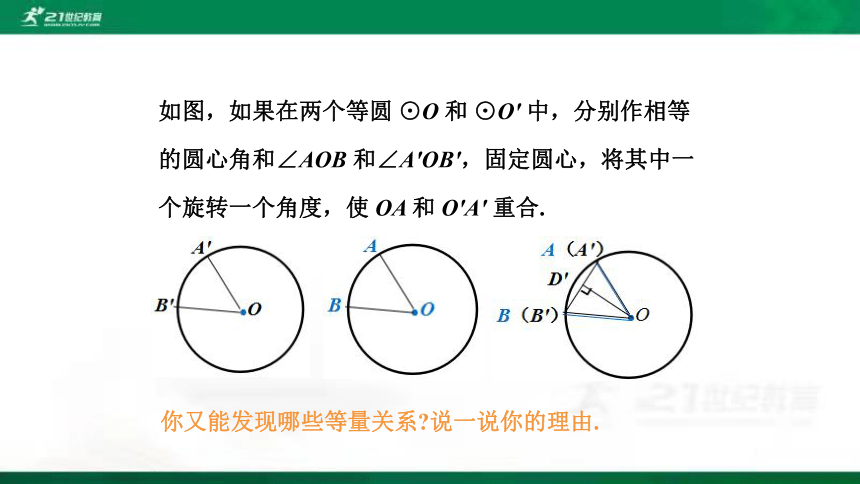
如图,如果在两个等圆 ⊙O 和 ⊙O′ 中,分别作相等
的圆心角和∠AOB 和∠A′OB′,固定圆心,将其中一
个旋转一个角度,使 OA 和 O′A′ 重合.
你又能发现哪些等量关系 说一说你的理由.
圆心角、弧、弦、弦心距之间的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
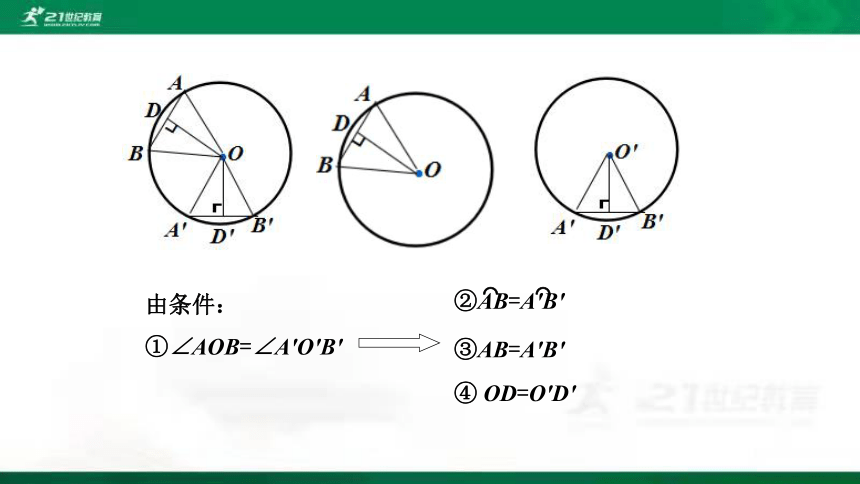
由条件:
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
在同圆或等圆中,如果交换下列条件:
① 两个圆心角;
② 两条弧;
③ 两条弦;
④ 两条弦心距.
你能得出什么结论?与同伴交流你的想法和理由.
用心想一想
如由条件:
②AB=A′B′
⌒ ⌒
①∠AOB=∠A′O′B′
③AB=A′B′
④ OD=O′D′
讲授新课
在同圆或等圆中,如果
①两个圆心角;
②两条弧;
③两条弦;
④两条弦心距中,有一组量相等,那么它们
所对应的其余各组量都分别相等.
如由条件:
①∠AOB=∠A′O′B′
④ OD=O′D′
③AB=A′B′
②AB=A′B′
⌒ ⌒
【例1】如图,点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点 A,B和C,D,求证:AB=CD.
M
证明:作OM⊥AB,ON⊥CD,M,N为垂足.
O
【例题】
N
1.已知:如图,AB,CD是⊙O的两条弦,OE,OF为AB,CD的弦心距,根据本节定理及推论填空:
(1)如果AB=CD,那么 ___________,________, _________.
(2)如果OE=OF,那么 ___________,________,__________.
∠AOB=∠COD OE=OF AB=CD
⌒
⌒
∠AOB=∠COD AB=CD AB=CD
⌒
⌒
【跟踪训练】
(3)如果 那么
____________,__________,_________.
(4)如果∠AOB=∠COD,那么
_________,________,_________.
OE=OF AB=CD
⌒
⌒
AB=CD
∠AOB=∠COD OE=OF
AB=CD
【例2】A,B分别为CD和EF的中点,AB分别交CD,EF于点M,N,且AM=BN.求证:CD=EF.
证明:连接OA,OB,设分别与CD,EF交于点F,G
∵A为 中点,B为 中点
∴OA⊥CD,OB⊥EF.
F
G
⌒
⌒
【例题】
故∠AFC=∠BGE=90°
又由OA=OB,
∴∠OAB=∠OBA,
且AM=BN,
∴△AFM≌△BGN,
∴AF=BG,
∴OF=OG,
∴DC=EF.
证明:分别作O1C1⊥A1B1,
O2C2 ⊥ A2B2,垂足分别
为C1 ,C2,
∵A1B2∥O102,
∴ O1C1= O2C2.
如图:⊙ 和⊙ 是两个等圆,直线 平行于 . 分别交⊙ 于点 , ,交⊙ 于点 , .求证:
【跟踪训练】
证明:
∴ AB=AC,
又∠ACB=60°,
∴△ABC是等边三角形, AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
·
A
B
C
O
∵
如图,在⊙O中, ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
△ABC是等腰三角形.
2.如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
【解析】
∵
,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版九年级下册数学
第三章 圆
3.2圆的对称性
情景导入
基础回顾
1. 什么是轴对称图形?我们以前学过哪些轴对称图形?
如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形.例如,线段、角、等腰三角形、矩形、菱形、等腰梯形、正方形.
2.我们所学的圆是不是轴对称图形呢?
.
圆是轴对称图形吗?如果是,它的对称轴是什么?你
能找到多少条对称轴?
你是用什么方法解决上述问题的
圆是中心对称图形吗?如果是,它的对称中心是什么?你能找到多少个对称中心?
你又是用什么方法解决这个问题的
圆是轴对称图形. 圆的对称轴是任意一条经过圆心的
直线,它有无数条对称轴.
●O
利用折叠的方法即可解决上述问题.
圆也是中心对称图形. 它的对称中
心就是圆心.
用旋转的方法即可解决这个问题.
这是圆特有的一个性质:圆的旋转不变性.
圆的对称性及特性
讲授新课
圆心角:顶点在圆心的角.
弦心距:过圆心作弦的垂线,圆心与垂足之间
的距离.
如图,在 ⊙O 中,分别作相等的圆心角 ∠AOB 和
∠A′OB′,将其中的一个旋转一个角度,使 OA 和
O′A′ 重合.
你能发现哪些等量关系 说一说你的理由.
如图,如果在两个等圆 ⊙O 和 ⊙O′ 中,分别作相等
的圆心角和∠AOB 和∠A′OB′,固定圆心,将其中一
个旋转一个角度,使 OA 和 O′A′ 重合.
你又能发现哪些等量关系 说一说你的理由.
圆心角、弧、弦、弦心距之间的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
由条件:
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
在同圆或等圆中,如果交换下列条件:
① 两个圆心角;
② 两条弧;
③ 两条弦;
④ 两条弦心距.
你能得出什么结论?与同伴交流你的想法和理由.
用心想一想
如由条件:
②AB=A′B′
⌒ ⌒
①∠AOB=∠A′O′B′
③AB=A′B′
④ OD=O′D′
讲授新课
在同圆或等圆中,如果
①两个圆心角;
②两条弧;
③两条弦;
④两条弦心距中,有一组量相等,那么它们
所对应的其余各组量都分别相等.
如由条件:
①∠AOB=∠A′O′B′
④ OD=O′D′
③AB=A′B′
②AB=A′B′
⌒ ⌒
【例1】如图,点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点 A,B和C,D,求证:AB=CD.
M
证明:作OM⊥AB,ON⊥CD,M,N为垂足.
O
【例题】
N
1.已知:如图,AB,CD是⊙O的两条弦,OE,OF为AB,CD的弦心距,根据本节定理及推论填空:
(1)如果AB=CD,那么 ___________,________, _________.
(2)如果OE=OF,那么 ___________,________,__________.
∠AOB=∠COD OE=OF AB=CD
⌒
⌒
∠AOB=∠COD AB=CD AB=CD
⌒
⌒
【跟踪训练】
(3)如果 那么
____________,__________,_________.
(4)如果∠AOB=∠COD,那么
_________,________,_________.
OE=OF AB=CD
⌒
⌒
AB=CD
∠AOB=∠COD OE=OF
AB=CD
【例2】A,B分别为CD和EF的中点,AB分别交CD,EF于点M,N,且AM=BN.求证:CD=EF.
证明:连接OA,OB,设分别与CD,EF交于点F,G
∵A为 中点,B为 中点
∴OA⊥CD,OB⊥EF.
F
G
⌒
⌒
【例题】
故∠AFC=∠BGE=90°
又由OA=OB,
∴∠OAB=∠OBA,
且AM=BN,
∴△AFM≌△BGN,
∴AF=BG,
∴OF=OG,
∴DC=EF.
证明:分别作O1C1⊥A1B1,
O2C2 ⊥ A2B2,垂足分别
为C1 ,C2,
∵A1B2∥O102,
∴ O1C1= O2C2.
如图:⊙ 和⊙ 是两个等圆,直线 平行于 . 分别交⊙ 于点 , ,交⊙ 于点 , .求证:
【跟踪训练】
证明:
∴ AB=AC,
又∠ACB=60°,
∴△ABC是等边三角形, AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
·
A
B
C
O
∵
如图,在⊙O中, ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
△ABC是等腰三角形.
2.如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
【解析】
∵
,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
