3.6.2 直线和圆的位置关系 课件(共35张PPT)
文档属性
| 名称 | 3.6.2 直线和圆的位置关系 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 574.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 20:24:32 | ||
图片预览







文档简介
(共35张PPT)
北师大版九年级下册数学
第三章 圆
3.6.2 直线和圆的位置关系
回顾旧知
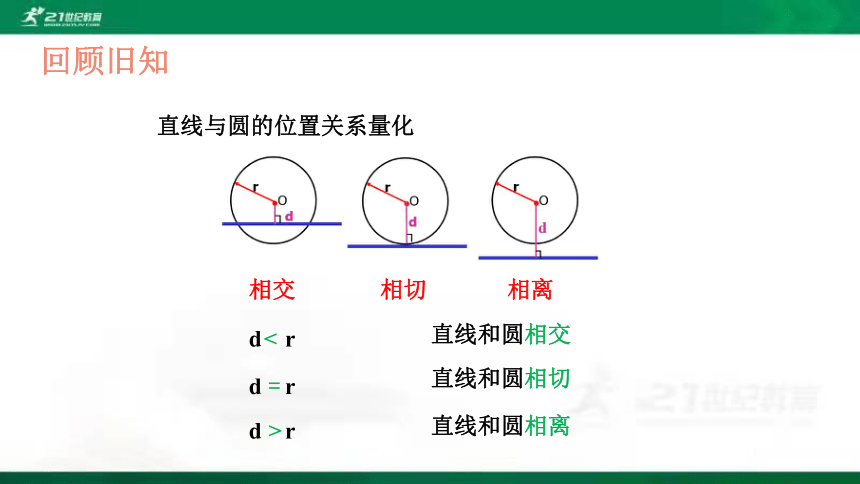
直线与圆的位置关系量化
直线和圆相交
d r
d r
直线和圆相切
直线和圆相离
d r
<
=
>
相离
相切
相交
情境引入
动手操作:在 ⊙O 中任取一点 A,连接 OA,过点 A 作直线 l⊥OA .
思 考:(可与同伴交流)
(1)圆心 O 到直线 l 的距离和圆的半径由什么关系?
(2)直线 l 与 ⊙O 的位置有什么关系?根据什么?
(3)由此你发现了什么?
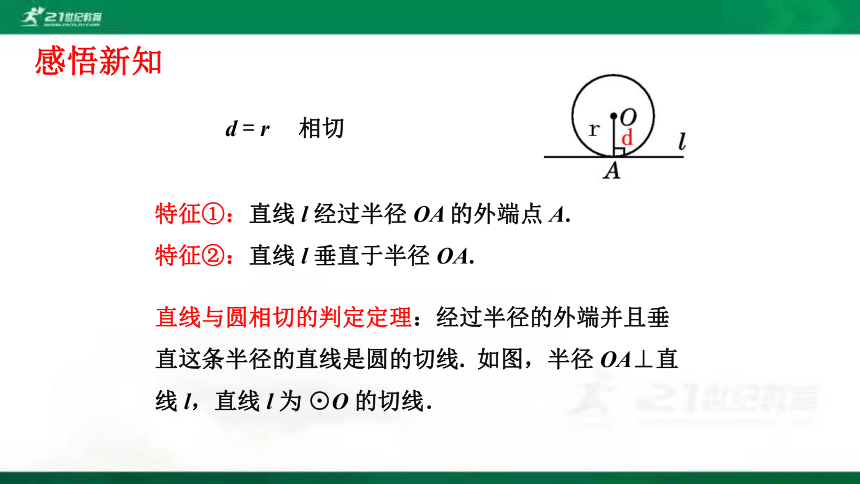
直线与圆相切的判定定理:经过半径的外端并且垂
直这条半径的直线是圆的切线. 如图,半径 OA⊥直
线 l,直线 l 为 ⊙O 的切线.
特征①:直线 l 经过半径 OA 的外端点 A.
特征②:直线 l 垂直于半径 OA.
d = r
相切
感悟新知
圆的切线的判定方法:
(1)概念:与圆有唯一公共点的直线是圆的切线.
(2)数量关系:到圆心的距离等于半径的直线是圆
的切线.
(3)判定定理:经过半径的外端并且垂直这条半径
的直线是圆的切线.
总结归纳
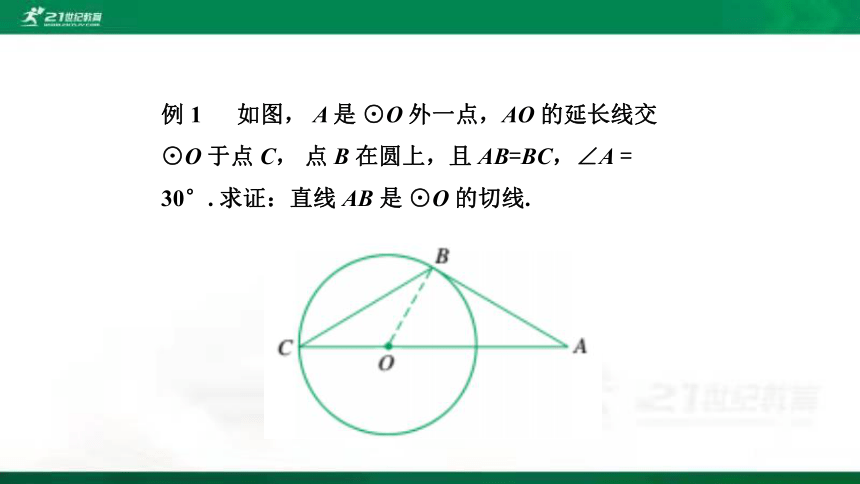
例 1 如图, A 是 ⊙O 外一点,AO 的延长线交
⊙O 于点 C, 点 B 在圆上,且 AB=BC,∠A =
30°. 求证:直线 AB 是 ⊙O 的切线.
证明:连接 OB.
∵OB=OC,AB=BC,∠A=30°,
∴∠OBC=∠C=∠A=30°,
∴∠AOB=∠C+∠OBC=60°.
∵∠ABO=180°-(∠AOB+∠A)=180°-
( 60°+30°)=90°,
∴AB⊥OB,
∴AB 为 ⊙O 的切线(经过半径的外端并且
垂直这条半径的直线是圆的切线).
练习
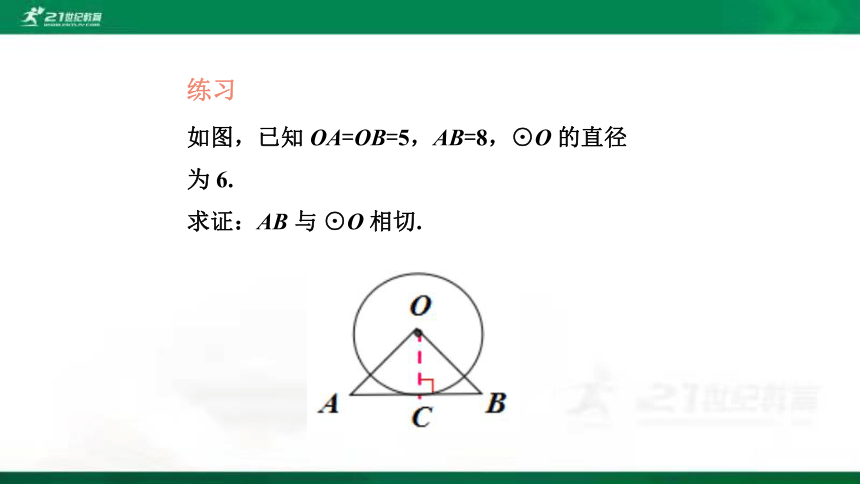
如图,已知 OA=OB=5,AB=8,⊙O 的直径为 6.
求证:AB 与 ⊙O 相切.
证明:过点 O 作 OC⊥AB.
∵OA=OB=5,AB=8,∴AC=BC=4.
∴在 Rt△AOC 中,OC=3.
又∵⊙O 的直径为 6,
∴OC=半径 r,
∴直线 AB 是⊙O 的切线.
有交点,连半径,证垂直;
无交点,作垂直,证 d=r.
实际应用
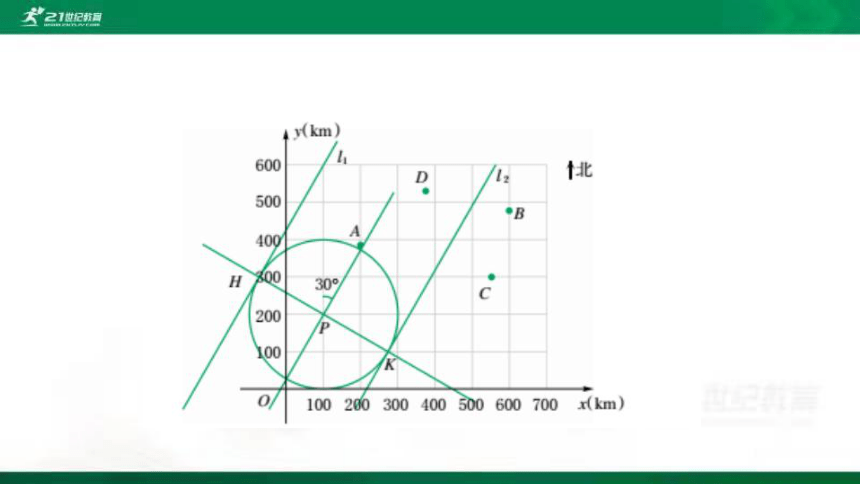
例 2 如图,台风中心 P(100,200)沿北偏东 30°方向移动,受台风影响区域的半径为 200 km,那么下列城市 A(200,380),B(600,480),C(550,300),D(370,540),哪些受到这次台风的影响,哪些不受到这次台风的影响?
合作学习
已知直线 AT 切 ⊙O 于点 A(切点),连接 OA,
则 OA 是半径. 问:
① OA 与 AT 垂直吗?
②过点 A 作 AT 的垂线,垂线过点 O 吗?
解:①经过切点的半径垂直于圆的切线.
②经过切点垂直于切线的直线必经过圆心.
圆的切线的性质:
经过切点的半径垂直于圆的切线.
拓展:
(1)切线和圆只有一个公共点.
(2)圆心到切线的距离等于半径.
(3)经过圆心垂直于切线的直线必经过切点.
(4)经过切点垂直于切线的直线必经过圆心.
总结归纳
例 3 木工师傅可以用角尺测量并计算出圆的半径. 如图, 用角尺的较短边紧靠 ⊙O 于点 A,并使较长边与 ⊙O 相切于点 C,记角尺的直角顶点为 B,量得 AB=8 cm,BC=16 cm. 求 ⊙O 的半径.
连接过切点的半径是常用的辅助线.
O
A
B
C
D
解:连接 OA,OC,过点 A 作 AD⊥OC 于点 D.
∵⊙O 与 BC 相切于点 C,∴OC⊥BC.
∵AB⊥BC,AD⊥OC,
∴四边形 ABCD 是矩形,
∴AD=BC,OD=OC-CD=OC-AB.
在 Rt△ADO 中,OA2 =AD2 +OD2,
即 r2 =(r-8)2 +162,解得 r=20.
∴ ⊙O 的半径为 20 cm.
例 4 如图,直线 AB 与 ⊙O 相切于点 C,AO 交⊙O 于点 D,连接 CD,OC.
求证:∠ACD = ∠COD.
证明:如图,作 OE丄CD 于点 E,
则∠COE+ ∠OCE= 90°.
∵⊙O 与 AB 相切于点 C,
∴OC丄AB(经过切点的半径垂直于圆的切线),
即∠ACD+ ∠OCE= 90°.
∴∠ACD= ∠COE.
∵△ODC 是等腰三角形,OE⊥CD,
∴ ∠COE= ∠COD, ∴∠ACD= ∠COD.
1. 切线的判定定理.
2. 判定一条直线是圆的切线的方法:
(1)定义:直线和圆有唯一公共点.
(2)数量关系:直线到圆心的距离等于半径.
(3)判定定理:经过半径的外端且与这条半径垂直的直线是圆的切线.
课堂小结
3. 辅助线作法:
(1)有公共点:作半径证垂直.
(2)无公共点:作垂直证半径.
4. 切线的性质:
(1)经过切点的半径垂直于圆的切线.
(2)经过切点垂直于切线的直线必经过圆心.
5. 切线性质的运用:
常用的辅助线是连接半径.
综合性较强,要联系许多其他图形的性质.
1.(青岛·中考)如图,在Rt△ABC中,∠C = 90°,∠B = 30°,BC = 4 cm,以点C为圆心,以2 cm的长为半径作圆,则⊙C与AB的位置关系是( )
A.相离 B.相切 C.相交 D.相切或相交
B
C
A
答案:B
2.(娄底·中考)在平面直角坐标系中,以点(3,2)为圆心、3为半径的圆,一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切 D.与x轴相交,与y轴相交
答案:C
3.(赤峰·中考)如图,⊙O的圆心到直线l的距离为3cm,⊙O的半径为1cm,将直线l向右(垂直于l的方向)平移,使l与⊙O相切,则平移的距离是( )
A.1cm B.2cm C.4cm D.2cm或4cm
答案:D
·O
l
【规律方法】直线与圆位置关系的判定可以从数的角度和形的角度进行判定,数的角度是圆心到直线的距离;形的角度是直线与圆的交点的个数.
4.(兰州·中考)如图,等边三角形的内切圆半径为1,那么这个等边三角形的边长为( )
答案:D
C.
D.
A.2 B.3
5.(黄冈·中考)如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=AB·AE,求证:DE是⊙O的切线.
证明:连接DC,DO,并延长DO交⊙O于F,连接AF.
∵AD2=AB·AE,∠BAD=∠DAE,
∴△BAD∽△DAE,∴∠ADB=∠E.
又∵∠ADB=∠ACB,
∴∠ACB=∠E,BC∥DE,
∴∠CDE=∠BCD=∠BAD=∠DAC,
又∵∠CAF=∠CDF,
∴∠FDE=∠CDE+∠CDF=∠DAC+∠CAF=∠DAF=90°,
故DE是⊙O的切线.
6.(德化·中考)如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD,AC分别交于点E,F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,
并证明你的结论.
(2)若tan∠ACB= ,BC=2,
求⊙O的半径.
【解析】(1)直线CE与⊙O相切.
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC ,
又 ∵∠ACB=∠DCE,
∴∠DAC=∠DCE,连接OE,则∠DAC=∠AEO=∠DCE,
∵∠DCE+∠DEC=90°,
∴∠AE0+∠DEC=90°,
∴∠OEC=90 °,
∴直线CE与⊙O相切.
BC=2 ∴AB=BCtan∠ACB=
AC= .
又∵∠ACB=∠DCE ∴tan∠DCE= ,
设⊙O的半径为r,则在Rt△COE中,
解得:r= .
(2)∵tan∠ACB=
∴DE=DC tan∠DCE=1,
在Rt△CDE中,CE=
得
,
,
7.(临沂·中考)如图,AB是半圆的直径,O为圆心,AD,BD是半圆的弦,且∠PDA=∠PBD.
(1)判断直线PD是否为⊙O的切线,并说明理由.
(2)如果∠BDE=60°, ,求PA的长.
【解析】(1)PD是⊙O的切线.
连接OD,∵OB=OD,
∴∠ODB=∠PBD.
又∵∠PDA=∠PBD.∴∠ODB=∠PDA.
又∵AB是半圆的直径,∴∠ADB=90°.
即∠ODB+∠ODA=90°. ∴∠ODA+∠PDA=90°,
即OD⊥PD.∴PD是⊙O的切线.
(2)∵∠BDE=60°,∠ODE=90°,∠ADB=90°,
∴∠ODB=30°,∠ODA=60°.
∵OA=OD,
∴△AOD是等边三角形.
∴∠POD=60°.
∴∠P=∠PDA=30°.
在直角△PDO中,设OD=x,
∴
∴x1=1,x2=-1(不合题意,舍去)
∴PA=1.
【规律方法】证明直线是否是圆的切线有两种辅助线的作法:(1)过圆心作已知直线的垂线,判定距离等于半径;(2)连接圆心与圆上的点,证垂直.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版九年级下册数学
第三章 圆
3.6.2 直线和圆的位置关系
回顾旧知
直线与圆的位置关系量化
直线和圆相交
d r
d r
直线和圆相切
直线和圆相离
d r
<
=
>
相离
相切
相交
情境引入
动手操作:在 ⊙O 中任取一点 A,连接 OA,过点 A 作直线 l⊥OA .
思 考:(可与同伴交流)
(1)圆心 O 到直线 l 的距离和圆的半径由什么关系?
(2)直线 l 与 ⊙O 的位置有什么关系?根据什么?
(3)由此你发现了什么?
直线与圆相切的判定定理:经过半径的外端并且垂
直这条半径的直线是圆的切线. 如图,半径 OA⊥直
线 l,直线 l 为 ⊙O 的切线.
特征①:直线 l 经过半径 OA 的外端点 A.
特征②:直线 l 垂直于半径 OA.
d = r
相切
感悟新知
圆的切线的判定方法:
(1)概念:与圆有唯一公共点的直线是圆的切线.
(2)数量关系:到圆心的距离等于半径的直线是圆
的切线.
(3)判定定理:经过半径的外端并且垂直这条半径
的直线是圆的切线.
总结归纳
例 1 如图, A 是 ⊙O 外一点,AO 的延长线交
⊙O 于点 C, 点 B 在圆上,且 AB=BC,∠A =
30°. 求证:直线 AB 是 ⊙O 的切线.
证明:连接 OB.
∵OB=OC,AB=BC,∠A=30°,
∴∠OBC=∠C=∠A=30°,
∴∠AOB=∠C+∠OBC=60°.
∵∠ABO=180°-(∠AOB+∠A)=180°-
( 60°+30°)=90°,
∴AB⊥OB,
∴AB 为 ⊙O 的切线(经过半径的外端并且
垂直这条半径的直线是圆的切线).
练习
如图,已知 OA=OB=5,AB=8,⊙O 的直径为 6.
求证:AB 与 ⊙O 相切.
证明:过点 O 作 OC⊥AB.
∵OA=OB=5,AB=8,∴AC=BC=4.
∴在 Rt△AOC 中,OC=3.
又∵⊙O 的直径为 6,
∴OC=半径 r,
∴直线 AB 是⊙O 的切线.
有交点,连半径,证垂直;
无交点,作垂直,证 d=r.
实际应用
例 2 如图,台风中心 P(100,200)沿北偏东 30°方向移动,受台风影响区域的半径为 200 km,那么下列城市 A(200,380),B(600,480),C(550,300),D(370,540),哪些受到这次台风的影响,哪些不受到这次台风的影响?
合作学习
已知直线 AT 切 ⊙O 于点 A(切点),连接 OA,
则 OA 是半径. 问:
① OA 与 AT 垂直吗?
②过点 A 作 AT 的垂线,垂线过点 O 吗?
解:①经过切点的半径垂直于圆的切线.
②经过切点垂直于切线的直线必经过圆心.
圆的切线的性质:
经过切点的半径垂直于圆的切线.
拓展:
(1)切线和圆只有一个公共点.
(2)圆心到切线的距离等于半径.
(3)经过圆心垂直于切线的直线必经过切点.
(4)经过切点垂直于切线的直线必经过圆心.
总结归纳
例 3 木工师傅可以用角尺测量并计算出圆的半径. 如图, 用角尺的较短边紧靠 ⊙O 于点 A,并使较长边与 ⊙O 相切于点 C,记角尺的直角顶点为 B,量得 AB=8 cm,BC=16 cm. 求 ⊙O 的半径.
连接过切点的半径是常用的辅助线.
O
A
B
C
D
解:连接 OA,OC,过点 A 作 AD⊥OC 于点 D.
∵⊙O 与 BC 相切于点 C,∴OC⊥BC.
∵AB⊥BC,AD⊥OC,
∴四边形 ABCD 是矩形,
∴AD=BC,OD=OC-CD=OC-AB.
在 Rt△ADO 中,OA2 =AD2 +OD2,
即 r2 =(r-8)2 +162,解得 r=20.
∴ ⊙O 的半径为 20 cm.
例 4 如图,直线 AB 与 ⊙O 相切于点 C,AO 交⊙O 于点 D,连接 CD,OC.
求证:∠ACD = ∠COD.
证明:如图,作 OE丄CD 于点 E,
则∠COE+ ∠OCE= 90°.
∵⊙O 与 AB 相切于点 C,
∴OC丄AB(经过切点的半径垂直于圆的切线),
即∠ACD+ ∠OCE= 90°.
∴∠ACD= ∠COE.
∵△ODC 是等腰三角形,OE⊥CD,
∴ ∠COE= ∠COD, ∴∠ACD= ∠COD.
1. 切线的判定定理.
2. 判定一条直线是圆的切线的方法:
(1)定义:直线和圆有唯一公共点.
(2)数量关系:直线到圆心的距离等于半径.
(3)判定定理:经过半径的外端且与这条半径垂直的直线是圆的切线.
课堂小结
3. 辅助线作法:
(1)有公共点:作半径证垂直.
(2)无公共点:作垂直证半径.
4. 切线的性质:
(1)经过切点的半径垂直于圆的切线.
(2)经过切点垂直于切线的直线必经过圆心.
5. 切线性质的运用:
常用的辅助线是连接半径.
综合性较强,要联系许多其他图形的性质.
1.(青岛·中考)如图,在Rt△ABC中,∠C = 90°,∠B = 30°,BC = 4 cm,以点C为圆心,以2 cm的长为半径作圆,则⊙C与AB的位置关系是( )
A.相离 B.相切 C.相交 D.相切或相交
B
C
A
答案:B
2.(娄底·中考)在平面直角坐标系中,以点(3,2)为圆心、3为半径的圆,一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切 D.与x轴相交,与y轴相交
答案:C
3.(赤峰·中考)如图,⊙O的圆心到直线l的距离为3cm,⊙O的半径为1cm,将直线l向右(垂直于l的方向)平移,使l与⊙O相切,则平移的距离是( )
A.1cm B.2cm C.4cm D.2cm或4cm
答案:D
·O
l
【规律方法】直线与圆位置关系的判定可以从数的角度和形的角度进行判定,数的角度是圆心到直线的距离;形的角度是直线与圆的交点的个数.
4.(兰州·中考)如图,等边三角形的内切圆半径为1,那么这个等边三角形的边长为( )
答案:D
C.
D.
A.2 B.3
5.(黄冈·中考)如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=AB·AE,求证:DE是⊙O的切线.
证明:连接DC,DO,并延长DO交⊙O于F,连接AF.
∵AD2=AB·AE,∠BAD=∠DAE,
∴△BAD∽△DAE,∴∠ADB=∠E.
又∵∠ADB=∠ACB,
∴∠ACB=∠E,BC∥DE,
∴∠CDE=∠BCD=∠BAD=∠DAC,
又∵∠CAF=∠CDF,
∴∠FDE=∠CDE+∠CDF=∠DAC+∠CAF=∠DAF=90°,
故DE是⊙O的切线.
6.(德化·中考)如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD,AC分别交于点E,F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,
并证明你的结论.
(2)若tan∠ACB= ,BC=2,
求⊙O的半径.
【解析】(1)直线CE与⊙O相切.
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC ,
又 ∵∠ACB=∠DCE,
∴∠DAC=∠DCE,连接OE,则∠DAC=∠AEO=∠DCE,
∵∠DCE+∠DEC=90°,
∴∠AE0+∠DEC=90°,
∴∠OEC=90 °,
∴直线CE与⊙O相切.
BC=2 ∴AB=BCtan∠ACB=
AC= .
又∵∠ACB=∠DCE ∴tan∠DCE= ,
设⊙O的半径为r,则在Rt△COE中,
解得:r= .
(2)∵tan∠ACB=
∴DE=DC tan∠DCE=1,
在Rt△CDE中,CE=
得
,
,
7.(临沂·中考)如图,AB是半圆的直径,O为圆心,AD,BD是半圆的弦,且∠PDA=∠PBD.
(1)判断直线PD是否为⊙O的切线,并说明理由.
(2)如果∠BDE=60°, ,求PA的长.
【解析】(1)PD是⊙O的切线.
连接OD,∵OB=OD,
∴∠ODB=∠PBD.
又∵∠PDA=∠PBD.∴∠ODB=∠PDA.
又∵AB是半圆的直径,∴∠ADB=90°.
即∠ODB+∠ODA=90°. ∴∠ODA+∠PDA=90°,
即OD⊥PD.∴PD是⊙O的切线.
(2)∵∠BDE=60°,∠ODE=90°,∠ADB=90°,
∴∠ODB=30°,∠ODA=60°.
∵OA=OD,
∴△AOD是等边三角形.
∴∠POD=60°.
∴∠P=∠PDA=30°.
在直角△PDO中,设OD=x,
∴
∴x1=1,x2=-1(不合题意,舍去)
∴PA=1.
【规律方法】证明直线是否是圆的切线有两种辅助线的作法:(1)过圆心作已知直线的垂线,判定距离等于半径;(2)连接圆心与圆上的点,证垂直.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
