上海市第三女子中学2021-2022学年高一上学期数学期末考试试题(word版含答案解析)
文档属性
| 名称 | 上海市第三女子中学2021-2022学年高一上学期数学期末考试试题(word版含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 111.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 14:13:26 | ||
图片预览



文档简介
上海市第三女子中学2021-2022学年高一上学期期末考试
数学试题
一、填空题(每小题3分,共36分)
1.函数y=log3(x﹣1)的定义域为 .
2.函数y=2x﹣3的零点是 .
3.已知cosα=,﹣<α<0,则sinα= .
4.已知函数,则f(1)的值等于 .
5.函数y=的值域是 .
6.函数f(x)=4x3+k +1(k∈R),若f(2)=8,则f(﹣2)的值为 .
7.已知实数a>0且a≠1,不论a取何值,函数y=ax﹣4+2的图像恒过一个定点,这个定点的坐标为 .
8.已知f(x)是定义在R上的奇函数,当x<0时,f(x)=2x+x,则当x>0时,f(x)= .
9.已知tanα=2,则的值为 .
10.若函数f(x)=(a>0,a≠1)是R上的严格减函数,则实数a的取值范围是 .
11.已知函数f(x)=x2﹣2ax+5(a>1)的定义域和值域均是[1,a],则实数a= .
12.已知M是满足下列性质的所有函数y=f(x)组成的集合:对任意x1,x2∈Df(其中Df为函数f(x)的定义域),均有|f(x1)﹣f(x2)|≤|x1﹣x2|成立.若函数,x∈
[﹣1,+∞)属于集合M,则实数a的取值范围为 .
二、选择题(每小题3分,共12分)
13.“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分也非必要条件
14.下列四组函数中,表示同一函数的是( )
A.f(x)=,g(x)=x﹣1
B.f(x)=x﹣1,g(t)=t﹣1
C.f(x)=log3x2,g(x)=2log3x
D.f(x)=x,g(x)=
15.函数f(x)=log2的图象( )
A.关于原点对称 B.关于直线y=﹣x对称
C.关于y轴对称 D.关于直线y=x对称
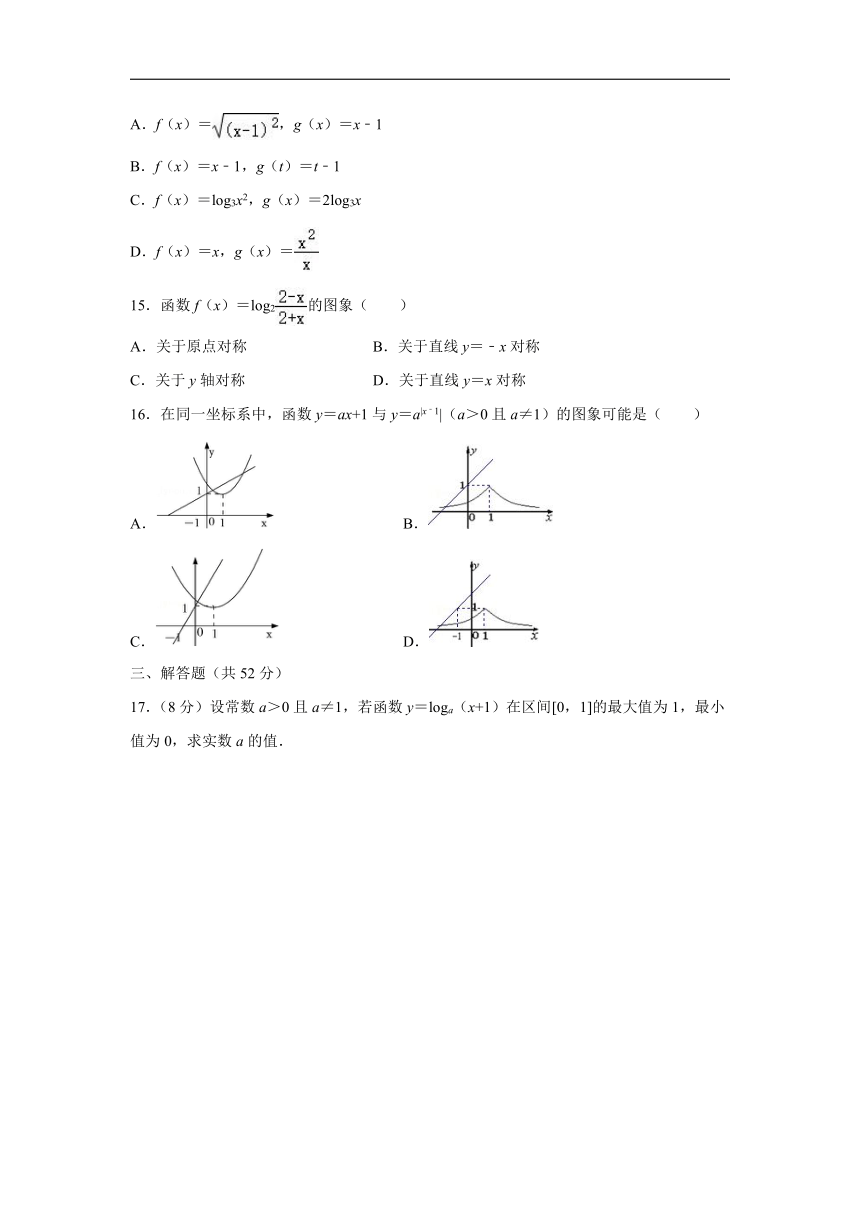
16.在同一坐标系中,函数y=ax+1与y=a|x﹣1|(a>0且a≠1)的图象可能是( )
A. B.
C. D.
三、解答题(共52分)
17.(8分)设常数a>0且a≠1,若函数y=loga(x+1)在区间[0,1]的最大值为1,最小值为0,求实数a的值.
18.(10分)已知幂函数f(x)=(m∈Z)的图像关于y轴对称,且在区间(0,+∞)上是严格增函数.
(1)求m的值;
(2)求满足不等式f(2a﹣1)<f(a+1)的实数a的取值范围.
19.(10分)已知函数f(x)=a﹣是R上的奇函数,a∈R.
(1)求a的值.
(2)用定义证明:函数f(x)是R上的严格增函数.
20.(10分)某辆汽车以x公里/小时速度在高速公路上匀速行驶(考虑到高速公路行车安全要求60≤x≤120)时,每小时的油耗(所需要的汽油量)为升.
(1)欲使每小时的油耗不超过9升,求x的取值范围;
(2)求该汽车行驶100公里的油耗y关于汽车行驶速度x的函数,并求y的最小值.
21.(14分)已知函数f(x)=ax2+bx+1(a,b为实数),x∈R.
(1)若函数f(x)的最小值是f(﹣1)=0,求a,b的值;
(2)在(1)的条件下,关于x的不等式f(x)+3≥kx在区间[﹣3,﹣1]上恒成立,求实数k的取值范围;
(3)若a>0,f(x)为偶函数,实数m,n满足m n<0,m+n>0,定义函数F(x)=,试判断F(m)+F(n)值的正负,并说明理由.
【参考答案】
一、填空题(每小题3分,共36分)
1.(1,+∞)
【解析】要使函数有意义,则x﹣1>0,得x>1,
即函数的定义域(1,+∞),
故答案为:(1,+∞).
2.log23
【解析】令2x﹣3=0,即2x=3,所以x=log23,
故函数的零点是:log23.故答案为:log23.
3.﹣
【解析】因为cosα=,﹣<α<0,
所以sinα=﹣=﹣=﹣.故答案为:﹣.
4.2
【解析】∵函数,∴f(1)=f(4)=log24=2,
故答案为:2.
5.(0,1]
【解析】因为x2+1≥1,所以,函数的值域为:(0,1].
6.﹣6
【解析】∵f(x)=4x3+k +1,
∴f(x)﹣1=4x3+k ,则f(x)﹣1为奇函数,
∴f(﹣2)﹣1=﹣[f(2)﹣1],
即f(﹣2)=﹣f(2)+1+1=﹣8+2=﹣6,故答案为:﹣6.
7.(4,3)
【解析】∵常数a>0且a≠1,无论a取何值,对于函数y=ax﹣4+2,
令x﹣4=0,求得x=4且y=3,故函数的图像恒过定点(4,3),
故答案为:(4,3).
8.x﹣()x
【解析】设x>0,则﹣x<0,
因为x<0时,f(x)=2x+x,且f(x)为奇函数,
所以f(﹣x)=2﹣x﹣x=﹣f(x),所以f(x)=x﹣()x.
故答案为:x﹣()x.
9.﹣
【解析】因为tanα=2,
所以====﹣.
故答案为:﹣.
10.[)
【解析】因为f(x)=(a>0,a≠1)是R上的严格减函数,
所以,解得,.故答案为:[).
11.2
【解析】∵二次函数f(x)=x2﹣2ax+5的图象是抛物线,开口向上,对称轴是x=﹣=a>1,∴f(x)=x2﹣2ax+5在[1,a]上是减函数,
又f(x)在[1,a]上的值域也是[1,a],
∴,即,解得a=2;故答案为:2.
12.[﹣1,1]
【解析】因为对任意x1,x2∈Df,均有|f(x1)﹣f(x2)|≤|x1﹣x2|成立,
若函数,x∈[﹣1,+∞)属于集合M,
则|﹣|≤|x1﹣x2|,x∈[﹣1,+∞)
化简得,|a|≤|(2+x1)(2+x2)|恒成立,
因为|(2+x1)≥1,(2+x2)|≥1,
所以|(2+x1)(2+x2)|≥1,故|a|≤1,解得﹣1≤a≤1.
故答案为:[﹣1,1].
二、选择题(每小题3分,共12分)
13.A
【解析】当时,则,
当时,α=或,k∈Z,
故“” “”,
“”不能推出“”,
所以“”是“”的充分不必要条件,故选:A.
14.B
【解析】A.∵f(x)==|x﹣1|,与g(x)的对应关系不同,∴不是同一函数;
B.f(x)与g(x)的定义域、对应关系和值域都相同,所以是同一函数;
C.∵f(x)的定义域为{x|x≠0},g(x)的定义域为{x|x>0},∴不是同一函数;
D..∵f(x)的定义域为R,g(x)的定义域为{x|x≠0},∴不是同一函数;故选:B.
15.A
【解析】∵函数f(x)=log2,∴>0,求得﹣2<x<2,可得函数的定义域为(﹣2,2),关于原点对称.
再根据 f(﹣x)=log=﹣f(x),可得函数f(x)为奇函数,故函数的图象关于原点对称,故选:A.
16.C
【解析】当a>1时,直线y=ax+1的斜率大于1,函数y=a|x﹣1|(a>0且a≠1)在(1,
+∞)上是增函数,选项C满足条件.
当1>a>0时,直线y=ax+1的斜率大于0且小于1,函数y=a|x﹣1|(a>0且a≠1)在(1,+∞)上是减函数,没有选项满足条件.
故选:C.
三、解答题(共52分)
17.解:y=loga(x+1)(a>0,且a≠1)在区间[0,1]上为单调函数,
当a>1时,有loga2=1,且loga1=0,解得a=2,
当0<a<1时,有loga2=0,且loga1=1,此时a不存在,
故答案为:2.
18.解:(1)由于f(x)的图象关于y轴对称,则f(x)是偶函数,
即﹣m2+4m是偶数,
由于f(x)在(0,+∞)内单调递增,所以﹣m2+4m>0,即0<m<4,
又m∈Z,故m可取1,2,3,
分别代入﹣m2+4m得3,4,3,
故取m=2,所以f(x)=x4,
(2)由(1)可得:不等式f(2a﹣1)<f(a+1) f(|2a﹣1|)<f(|a+1|) |2a﹣1|<|a+1| 0<a<2,
故实数a的取值范围是(0,2).
19.解:(1)由奇函数性质可得,f(0)=a﹣1=0,
所以a=1,此时f(x)=1﹣=,f(﹣x)===﹣f(x)满足题意,
故a=1;
(2)证明:设x1<x2,则<0,
f(x1)﹣f(x2)==<0,
所以f(x1)<f(x2),
所以f(x)在R上是增函数.
20.解:(1)由题意,令×(x﹣100+)≤9,
化简得x2﹣145x+4500≤0,解得45≤x≤100;
又因为60≤x≤120,
所以欲使每小时的油耗不超过9升,x的取值范围是[60,100];
(2)设该汽车行驶100公里的油耗为y;
则y= (x﹣100+)=90000+,(其中60≤x≤120);
由60≤x≤120,知∈[,],
所以x=90时,汽车行驶100公里的油耗取得最小值为升.
21.解:(1)由题意得,,解得a=1,b=2;
(2)由(1)得,f(x)=x2+2x+1,
由f(x)+3≥kx在区间[﹣3,﹣1]上恒成立,得x2+2x+4≥kx在区间[﹣3,﹣1]上恒成立,
即k≥x+在[﹣3,﹣1]上恒成立,则k≥(x+)max,
结合对勾函数的单调性可知,y=x+在[﹣3,﹣1]上先增后减,
当x=﹣2时,函数取得最大值﹣2,所以k≥﹣2,
所以k的范围为[﹣2,+∞);
(3)F(m)+F(n)>0.证明如下:
因为f(x)为偶函数,所以b=0,f(x)=ax2+1,
所以F(x)=,
因为m n<0,m+n>0,则m,n异号,不妨设m>0,n<0,
则m>﹣n>0,
F(m)+F(n)=f(m)﹣f(n)=am2+1﹣2﹣1=a(m﹣n)(m+n)>0,
所以F(m)+F(n)>0.
数学试题
一、填空题(每小题3分,共36分)
1.函数y=log3(x﹣1)的定义域为 .
2.函数y=2x﹣3的零点是 .
3.已知cosα=,﹣<α<0,则sinα= .
4.已知函数,则f(1)的值等于 .
5.函数y=的值域是 .
6.函数f(x)=4x3+k +1(k∈R),若f(2)=8,则f(﹣2)的值为 .
7.已知实数a>0且a≠1,不论a取何值,函数y=ax﹣4+2的图像恒过一个定点,这个定点的坐标为 .
8.已知f(x)是定义在R上的奇函数,当x<0时,f(x)=2x+x,则当x>0时,f(x)= .
9.已知tanα=2,则的值为 .
10.若函数f(x)=(a>0,a≠1)是R上的严格减函数,则实数a的取值范围是 .
11.已知函数f(x)=x2﹣2ax+5(a>1)的定义域和值域均是[1,a],则实数a= .
12.已知M是满足下列性质的所有函数y=f(x)组成的集合:对任意x1,x2∈Df(其中Df为函数f(x)的定义域),均有|f(x1)﹣f(x2)|≤|x1﹣x2|成立.若函数,x∈
[﹣1,+∞)属于集合M,则实数a的取值范围为 .
二、选择题(每小题3分,共12分)
13.“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分也非必要条件
14.下列四组函数中,表示同一函数的是( )
A.f(x)=,g(x)=x﹣1
B.f(x)=x﹣1,g(t)=t﹣1
C.f(x)=log3x2,g(x)=2log3x
D.f(x)=x,g(x)=
15.函数f(x)=log2的图象( )
A.关于原点对称 B.关于直线y=﹣x对称
C.关于y轴对称 D.关于直线y=x对称
16.在同一坐标系中,函数y=ax+1与y=a|x﹣1|(a>0且a≠1)的图象可能是( )
A. B.
C. D.
三、解答题(共52分)
17.(8分)设常数a>0且a≠1,若函数y=loga(x+1)在区间[0,1]的最大值为1,最小值为0,求实数a的值.
18.(10分)已知幂函数f(x)=(m∈Z)的图像关于y轴对称,且在区间(0,+∞)上是严格增函数.
(1)求m的值;
(2)求满足不等式f(2a﹣1)<f(a+1)的实数a的取值范围.
19.(10分)已知函数f(x)=a﹣是R上的奇函数,a∈R.
(1)求a的值.
(2)用定义证明:函数f(x)是R上的严格增函数.
20.(10分)某辆汽车以x公里/小时速度在高速公路上匀速行驶(考虑到高速公路行车安全要求60≤x≤120)时,每小时的油耗(所需要的汽油量)为升.
(1)欲使每小时的油耗不超过9升,求x的取值范围;
(2)求该汽车行驶100公里的油耗y关于汽车行驶速度x的函数,并求y的最小值.
21.(14分)已知函数f(x)=ax2+bx+1(a,b为实数),x∈R.
(1)若函数f(x)的最小值是f(﹣1)=0,求a,b的值;
(2)在(1)的条件下,关于x的不等式f(x)+3≥kx在区间[﹣3,﹣1]上恒成立,求实数k的取值范围;
(3)若a>0,f(x)为偶函数,实数m,n满足m n<0,m+n>0,定义函数F(x)=,试判断F(m)+F(n)值的正负,并说明理由.
【参考答案】
一、填空题(每小题3分,共36分)
1.(1,+∞)
【解析】要使函数有意义,则x﹣1>0,得x>1,
即函数的定义域(1,+∞),
故答案为:(1,+∞).
2.log23
【解析】令2x﹣3=0,即2x=3,所以x=log23,
故函数的零点是:log23.故答案为:log23.
3.﹣
【解析】因为cosα=,﹣<α<0,
所以sinα=﹣=﹣=﹣.故答案为:﹣.
4.2
【解析】∵函数,∴f(1)=f(4)=log24=2,
故答案为:2.
5.(0,1]
【解析】因为x2+1≥1,所以,函数的值域为:(0,1].
6.﹣6
【解析】∵f(x)=4x3+k +1,
∴f(x)﹣1=4x3+k ,则f(x)﹣1为奇函数,
∴f(﹣2)﹣1=﹣[f(2)﹣1],
即f(﹣2)=﹣f(2)+1+1=﹣8+2=﹣6,故答案为:﹣6.
7.(4,3)
【解析】∵常数a>0且a≠1,无论a取何值,对于函数y=ax﹣4+2,
令x﹣4=0,求得x=4且y=3,故函数的图像恒过定点(4,3),
故答案为:(4,3).
8.x﹣()x
【解析】设x>0,则﹣x<0,
因为x<0时,f(x)=2x+x,且f(x)为奇函数,
所以f(﹣x)=2﹣x﹣x=﹣f(x),所以f(x)=x﹣()x.
故答案为:x﹣()x.
9.﹣
【解析】因为tanα=2,
所以====﹣.
故答案为:﹣.
10.[)
【解析】因为f(x)=(a>0,a≠1)是R上的严格减函数,
所以,解得,.故答案为:[).
11.2
【解析】∵二次函数f(x)=x2﹣2ax+5的图象是抛物线,开口向上,对称轴是x=﹣=a>1,∴f(x)=x2﹣2ax+5在[1,a]上是减函数,
又f(x)在[1,a]上的值域也是[1,a],
∴,即,解得a=2;故答案为:2.
12.[﹣1,1]
【解析】因为对任意x1,x2∈Df,均有|f(x1)﹣f(x2)|≤|x1﹣x2|成立,
若函数,x∈[﹣1,+∞)属于集合M,
则|﹣|≤|x1﹣x2|,x∈[﹣1,+∞)
化简得,|a|≤|(2+x1)(2+x2)|恒成立,
因为|(2+x1)≥1,(2+x2)|≥1,
所以|(2+x1)(2+x2)|≥1,故|a|≤1,解得﹣1≤a≤1.
故答案为:[﹣1,1].
二、选择题(每小题3分,共12分)
13.A
【解析】当时,则,
当时,α=或,k∈Z,
故“” “”,
“”不能推出“”,
所以“”是“”的充分不必要条件,故选:A.
14.B
【解析】A.∵f(x)==|x﹣1|,与g(x)的对应关系不同,∴不是同一函数;
B.f(x)与g(x)的定义域、对应关系和值域都相同,所以是同一函数;
C.∵f(x)的定义域为{x|x≠0},g(x)的定义域为{x|x>0},∴不是同一函数;
D..∵f(x)的定义域为R,g(x)的定义域为{x|x≠0},∴不是同一函数;故选:B.
15.A
【解析】∵函数f(x)=log2,∴>0,求得﹣2<x<2,可得函数的定义域为(﹣2,2),关于原点对称.
再根据 f(﹣x)=log=﹣f(x),可得函数f(x)为奇函数,故函数的图象关于原点对称,故选:A.
16.C
【解析】当a>1时,直线y=ax+1的斜率大于1,函数y=a|x﹣1|(a>0且a≠1)在(1,
+∞)上是增函数,选项C满足条件.
当1>a>0时,直线y=ax+1的斜率大于0且小于1,函数y=a|x﹣1|(a>0且a≠1)在(1,+∞)上是减函数,没有选项满足条件.
故选:C.
三、解答题(共52分)
17.解:y=loga(x+1)(a>0,且a≠1)在区间[0,1]上为单调函数,
当a>1时,有loga2=1,且loga1=0,解得a=2,
当0<a<1时,有loga2=0,且loga1=1,此时a不存在,
故答案为:2.
18.解:(1)由于f(x)的图象关于y轴对称,则f(x)是偶函数,
即﹣m2+4m是偶数,
由于f(x)在(0,+∞)内单调递增,所以﹣m2+4m>0,即0<m<4,
又m∈Z,故m可取1,2,3,
分别代入﹣m2+4m得3,4,3,
故取m=2,所以f(x)=x4,
(2)由(1)可得:不等式f(2a﹣1)<f(a+1) f(|2a﹣1|)<f(|a+1|) |2a﹣1|<|a+1| 0<a<2,
故实数a的取值范围是(0,2).
19.解:(1)由奇函数性质可得,f(0)=a﹣1=0,
所以a=1,此时f(x)=1﹣=,f(﹣x)===﹣f(x)满足题意,
故a=1;
(2)证明:设x1<x2,则<0,
f(x1)﹣f(x2)==<0,
所以f(x1)<f(x2),
所以f(x)在R上是增函数.
20.解:(1)由题意,令×(x﹣100+)≤9,
化简得x2﹣145x+4500≤0,解得45≤x≤100;
又因为60≤x≤120,
所以欲使每小时的油耗不超过9升,x的取值范围是[60,100];
(2)设该汽车行驶100公里的油耗为y;
则y= (x﹣100+)=90000+,(其中60≤x≤120);
由60≤x≤120,知∈[,],
所以x=90时,汽车行驶100公里的油耗取得最小值为升.
21.解:(1)由题意得,,解得a=1,b=2;
(2)由(1)得,f(x)=x2+2x+1,
由f(x)+3≥kx在区间[﹣3,﹣1]上恒成立,得x2+2x+4≥kx在区间[﹣3,﹣1]上恒成立,
即k≥x+在[﹣3,﹣1]上恒成立,则k≥(x+)max,
结合对勾函数的单调性可知,y=x+在[﹣3,﹣1]上先增后减,
当x=﹣2时,函数取得最大值﹣2,所以k≥﹣2,
所以k的范围为[﹣2,+∞);
(3)F(m)+F(n)>0.证明如下:
因为f(x)为偶函数,所以b=0,f(x)=ax2+1,
所以F(x)=,
因为m n<0,m+n>0,则m,n异号,不妨设m>0,n<0,
则m>﹣n>0,
F(m)+F(n)=f(m)﹣f(n)=am2+1﹣2﹣1=a(m﹣n)(m+n)>0,
所以F(m)+F(n)>0.
同课章节目录
