3.7切线长定理 课件(共25张PPT)
文档属性
| 名称 | 3.7切线长定理 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 506.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 20:27:45 | ||
图片预览

文档简介
(共25张PPT)
北师大版九年级下册数学
第三章 圆
*3.7切线长定理
O
A
B
P
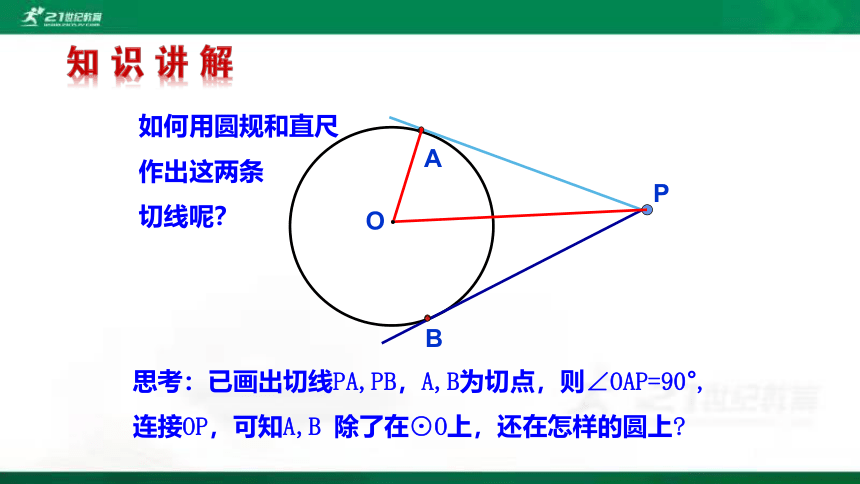
如何用圆规和直尺
作出这两条
切线呢?
.
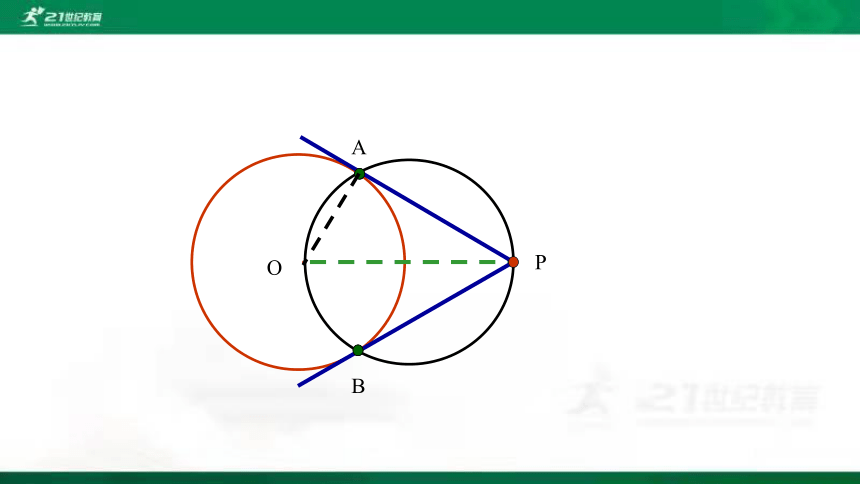
思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°,
连接OP,可知A,B 除了在⊙O上,还在怎样的圆上
O
·
P
A
B
O
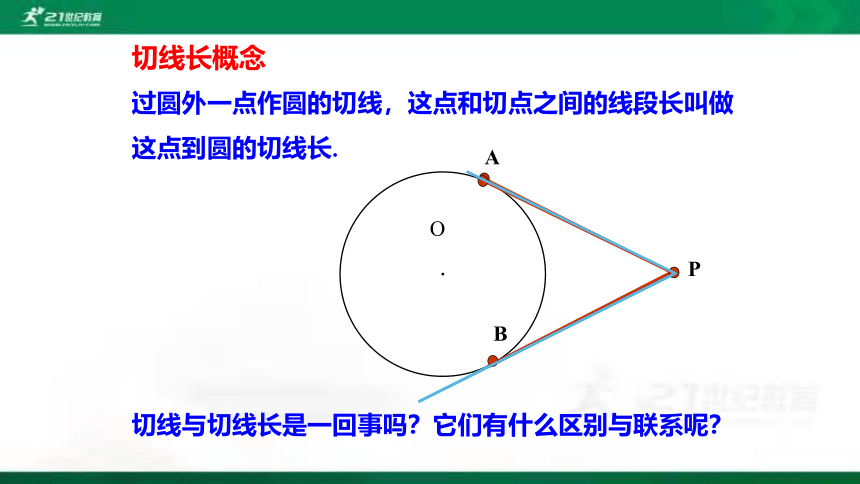
过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
·
O
P
A
B
切线与切线长是一回事吗?它们有什么区别与联系呢?
切线长概念
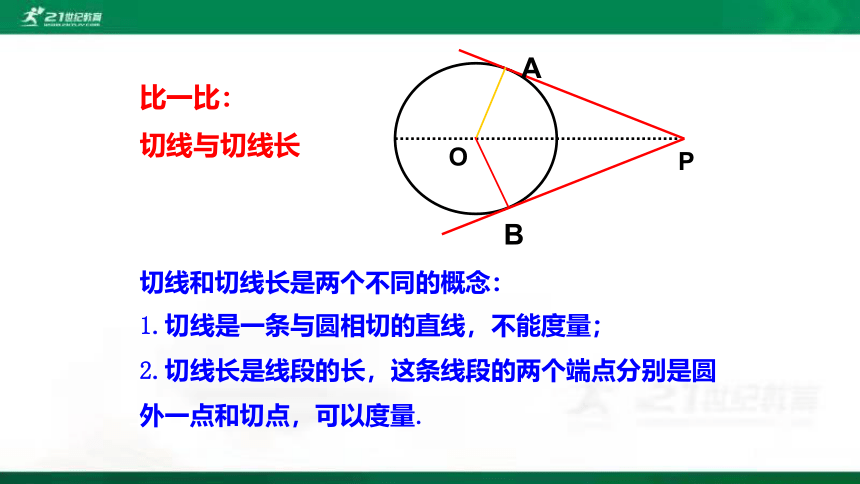
切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
O
P
A
B
比一比:
切线与切线长
O
A
B
P
1
2
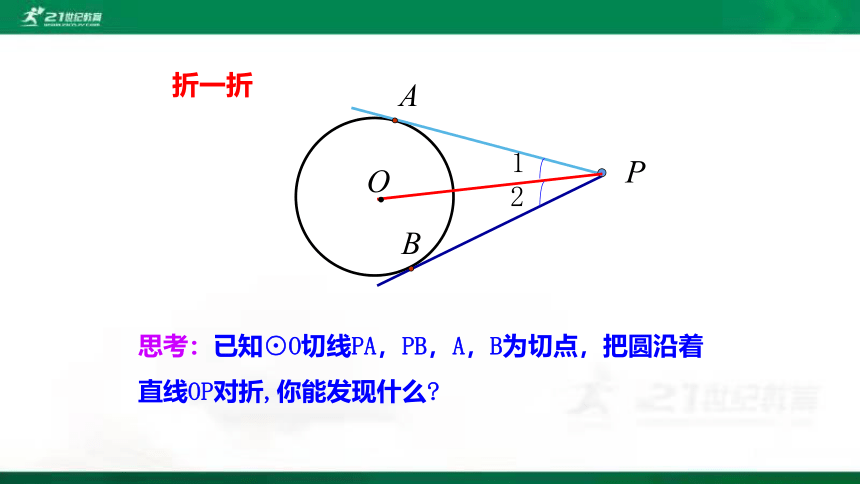
思考:已知⊙O切线PA,PB,A,B为切点,把圆沿着直线OP对折,你能发现什么
折一折
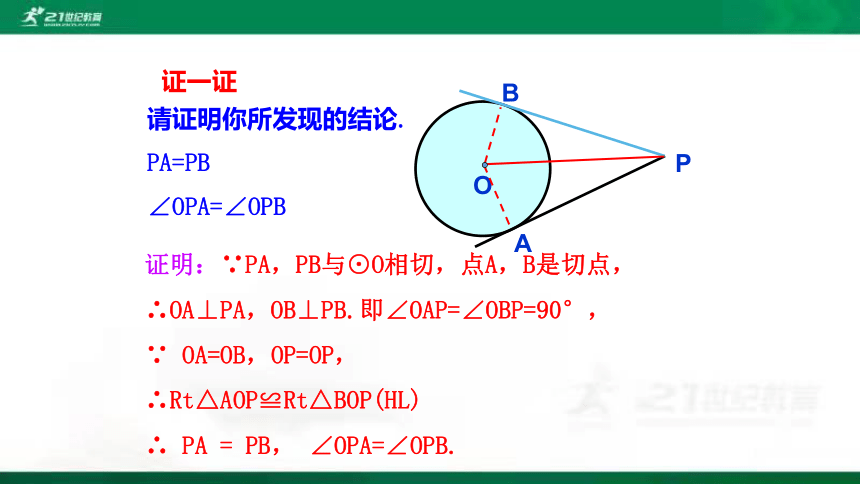
请证明你所发现的结论.
A
P
O
B
PA=PB
∠OPA=∠OPB
证明:∵PA,PB与⊙O相切,点A,B是切点,
∴OA⊥PA,OB⊥PB.即∠OAP=∠OBP=90°,
∵ OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB, ∠OPA=∠OPB.
证一证
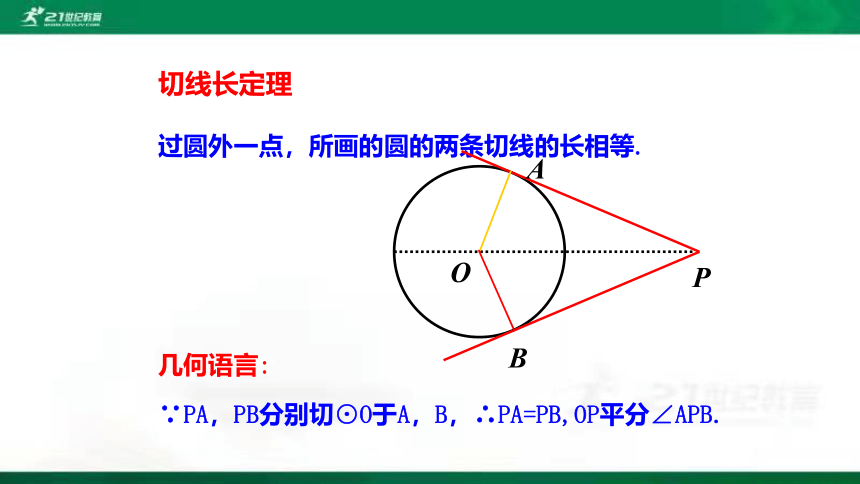
切线长定理
∵PA,PB分别切⊙O于A,B,∴PA=PB,OP平分∠APB.
过圆外一点,所画的圆的两条切线的长相等.
几何语言:
O
P
A
B
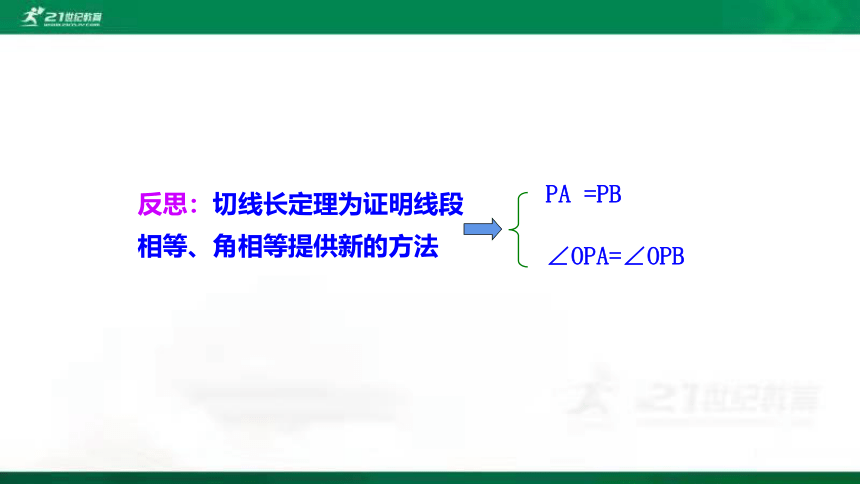
反思:切线长定理为证明线段相等、角相等提供新的方法
PA =PB
∠OPA=∠OPB
切线长问题辅助线添加方法
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
方法归纳
例 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=(9-x)cm,
BF=BD=AB-AF=(13-x)cm.
想一想:图中你能找出哪些相等的线段?理由是什么?
A
C
B
E
D
F
O
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
∴ AF=4cm,BD=9cm,CE=5cm.
方法小结:关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
解得 x=4.
A
C
B
E
D
F
O
例 如图,Rt△ABC中,∠C=90°,BC=a,AC=b, AB=c,⊙O为Rt△ABC的内切圆. 求:Rt△ABC的内切圆的半径 r.
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
解:设Rt△ABC的内切圆与三边相切
于D、E、F,连接OD、OE、OF,则
OD⊥AC,OE⊥BC,OF⊥AB.
B
·
A
C
E
D
F
O
设AD= x , BE= y ,CE= r
则有
x+r=b
y+r=a
x+y=c
解得
r=
a+b-c
2
B
·
A
C
E
D
F
O
设Rt△ABC的直角边为a、b,斜边为c,则Rt△ABC的内切圆的半径 r= 或r= (前面课时已证明).
a+b-c
2
ab
a+b+c
知识拓展
1、如图,直尺、三角尺均和圆O相切,AB=8 cm,
求圆O的直径.
练一练
导引:
连接OE,OA,OB,根据切线长定理和切线性质可
得∠OBA=90°,∠OAE=∠OAB= ∠BAC,求
∠BAC即可求出∠OAB和∠BOA,进而求出OA,
再根据勾股定理求出OB即可.
解:
如图,连接OE,OA,OB.
∵AC,AB都是⊙O的切线,切点分别是E,B,
∴∠OBA=90°,∠OAE=∠OAB= ∠BAC.
∵∠CAD=60°,∴∠BAC=120°,
∴∠OAB= ×120°=60°,
∴∠BOA=30°,∴OA=2AB=16 cm,
由勾股定理得OB= (cm),
即⊙O的半径是 cm,∴⊙O的直径是 cm.
2、如图,PA,PB是⊙O的切线,A,B是切点,点C是 上一点,过点C作⊙O的切线分别交PA,PB于点D,E.已知∠APB=60°,⊙O的半径为 ,则△PDE的周长为________,∠DOE的度数为________.
60°
6
A
P
B
D
C
E
导引:
如图,连接PO,CO,AO,BO,DO,EO,由切线长
定理知PA=PB,DC=DA,EC=EB,因而△PDE的
周长可转化为PA+PB,即2PA.又由切线长定理易得
∠DOC= ∠AOC,∠EOC= ∠BOC,∴∠DOE=
(∠AOC+∠BOC)= ∠AOB.由∠APB=60°得
∠APO=30°.又∵AO= ,
由切线的性质得∠PAO=90°,∠PBO=90°,
∴PO= ,∠AOB=180°-∠APB=120°.
∴PA= =3,∠DOE= ∠AOB=60°.
1 下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆
的半径
课堂练习
C
如图,PA,PB是⊙O的切线,且∠APB=40°,
下列结论不正确的是( )
A.PA=PB
B.∠APO=20°
C.∠OBP=70°
D.∠AOP=70°
C
如图,PA和PB是⊙O的切线,点A和B
是切点,AC是⊙O的直径,已知∠P=40°,则
∠ACB的大小是( )
A.60°
B.65°
C.70°
D.75°
C
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版九年级下册数学
第三章 圆
*3.7切线长定理
O
A
B
P
如何用圆规和直尺
作出这两条
切线呢?
.
思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°,
连接OP,可知A,B 除了在⊙O上,还在怎样的圆上
O
·
P
A
B
O
过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
·
O
P
A
B
切线与切线长是一回事吗?它们有什么区别与联系呢?
切线长概念
切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
O
P
A
B
比一比:
切线与切线长
O
A
B
P
1
2
思考:已知⊙O切线PA,PB,A,B为切点,把圆沿着直线OP对折,你能发现什么
折一折
请证明你所发现的结论.
A
P
O
B
PA=PB
∠OPA=∠OPB
证明:∵PA,PB与⊙O相切,点A,B是切点,
∴OA⊥PA,OB⊥PB.即∠OAP=∠OBP=90°,
∵ OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB, ∠OPA=∠OPB.
证一证
切线长定理
∵PA,PB分别切⊙O于A,B,∴PA=PB,OP平分∠APB.
过圆外一点,所画的圆的两条切线的长相等.
几何语言:
O
P
A
B
反思:切线长定理为证明线段相等、角相等提供新的方法
PA =PB
∠OPA=∠OPB
切线长问题辅助线添加方法
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
方法归纳
例 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=(9-x)cm,
BF=BD=AB-AF=(13-x)cm.
想一想:图中你能找出哪些相等的线段?理由是什么?
A
C
B
E
D
F
O
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
∴ AF=4cm,BD=9cm,CE=5cm.
方法小结:关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
解得 x=4.
A
C
B
E
D
F
O
例 如图,Rt△ABC中,∠C=90°,BC=a,AC=b, AB=c,⊙O为Rt△ABC的内切圆. 求:Rt△ABC的内切圆的半径 r.
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
解:设Rt△ABC的内切圆与三边相切
于D、E、F,连接OD、OE、OF,则
OD⊥AC,OE⊥BC,OF⊥AB.
B
·
A
C
E
D
F
O
设AD= x , BE= y ,CE= r
则有
x+r=b
y+r=a
x+y=c
解得
r=
a+b-c
2
B
·
A
C
E
D
F
O
设Rt△ABC的直角边为a、b,斜边为c,则Rt△ABC的内切圆的半径 r= 或r= (前面课时已证明).
a+b-c
2
ab
a+b+c
知识拓展
1、如图,直尺、三角尺均和圆O相切,AB=8 cm,
求圆O的直径.
练一练
导引:
连接OE,OA,OB,根据切线长定理和切线性质可
得∠OBA=90°,∠OAE=∠OAB= ∠BAC,求
∠BAC即可求出∠OAB和∠BOA,进而求出OA,
再根据勾股定理求出OB即可.
解:
如图,连接OE,OA,OB.
∵AC,AB都是⊙O的切线,切点分别是E,B,
∴∠OBA=90°,∠OAE=∠OAB= ∠BAC.
∵∠CAD=60°,∴∠BAC=120°,
∴∠OAB= ×120°=60°,
∴∠BOA=30°,∴OA=2AB=16 cm,
由勾股定理得OB= (cm),
即⊙O的半径是 cm,∴⊙O的直径是 cm.
2、如图,PA,PB是⊙O的切线,A,B是切点,点C是 上一点,过点C作⊙O的切线分别交PA,PB于点D,E.已知∠APB=60°,⊙O的半径为 ,则△PDE的周长为________,∠DOE的度数为________.
60°
6
A
P
B
D
C
E
导引:
如图,连接PO,CO,AO,BO,DO,EO,由切线长
定理知PA=PB,DC=DA,EC=EB,因而△PDE的
周长可转化为PA+PB,即2PA.又由切线长定理易得
∠DOC= ∠AOC,∠EOC= ∠BOC,∴∠DOE=
(∠AOC+∠BOC)= ∠AOB.由∠APB=60°得
∠APO=30°.又∵AO= ,
由切线的性质得∠PAO=90°,∠PBO=90°,
∴PO= ,∠AOB=180°-∠APB=120°.
∴PA= =3,∠DOE= ∠AOB=60°.
1 下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆
的半径
课堂练习
C
如图,PA,PB是⊙O的切线,且∠APB=40°,
下列结论不正确的是( )
A.PA=PB
B.∠APO=20°
C.∠OBP=70°
D.∠AOP=70°
C
如图,PA和PB是⊙O的切线,点A和B
是切点,AC是⊙O的直径,已知∠P=40°,则
∠ACB的大小是( )
A.60°
B.65°
C.70°
D.75°
C
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
