2.1两条直线的位置关系 课件(共44张PPT)
文档属性
| 名称 | 2.1两条直线的位置关系 课件(共44张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 13:24:27 | ||
图片预览




文档简介
(共44张PPT)
第二章 平行线与相交线
2.1 两条直线的位置关系
北师大版 七年级下册数学
观察下列图片,说一说直线与直线的位置关系.
情景引入
生活中处处可见道路、房屋、山川、桥梁.在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线.
在同一平面内,两条直线的位置关系有相交和平行两种.若两条直线只有一个公共点,我们称这两条直线为相交线.在同一平面内,不相交的两条直线叫作平行线.
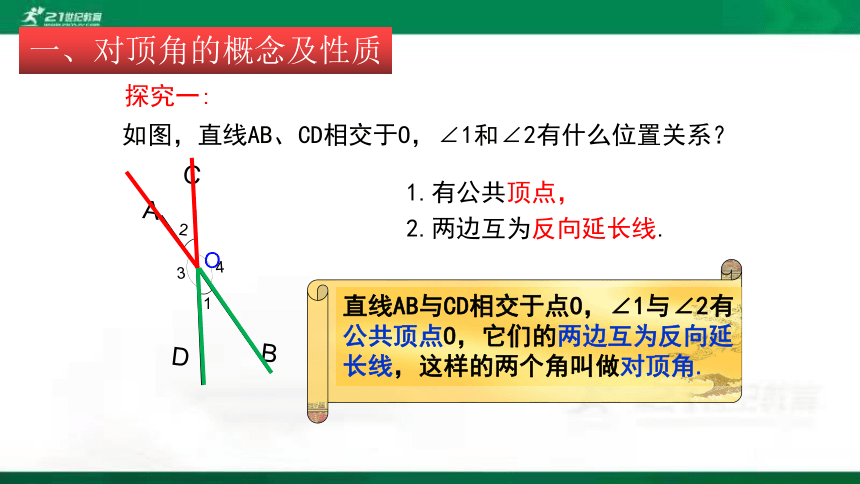
如图,直线AB、CD相交于O,∠1和∠2有什么位置关系?
2
1
A
B
C
D
O
3
4
探究一:
1.有公共顶点,
2.两边互为反向延长线.
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角.
一、对顶角的概念及性质
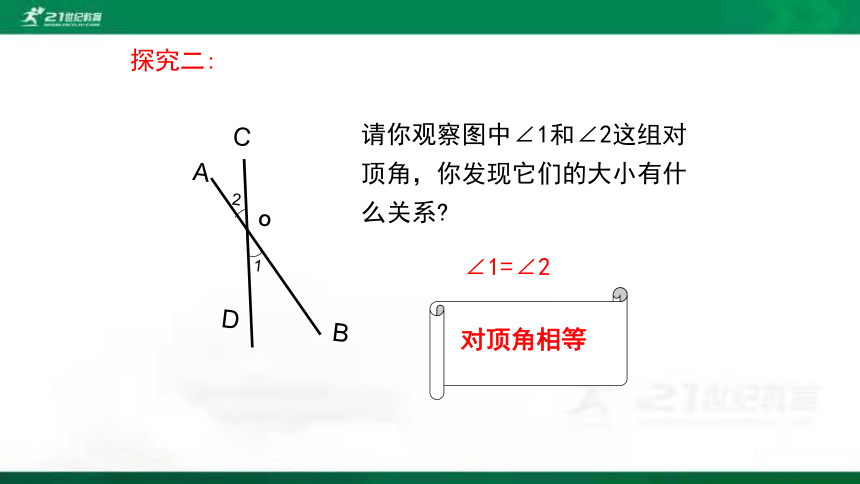
请你观察图中∠1和∠2这组对顶角,你发现它们的大小有什么关系
2
1
A
B
C
D
O
探究二:
∠1=∠2
对顶角相等
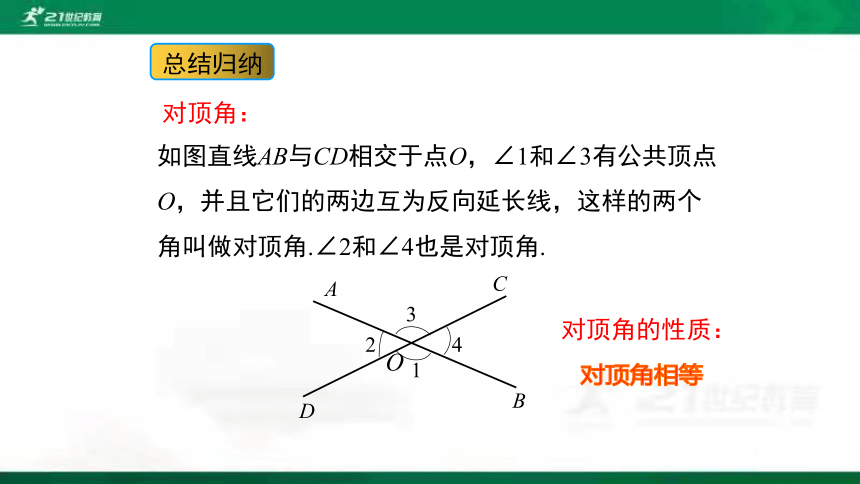
如图直线AB与CD相交于点O,∠1和∠3有公共顶点O,并且它们的两边互为反向延长线,这样的两个角叫做对顶角.∠2和∠4也是对顶角.
对顶角:
A
O
C
B
D
1
3
2
4
总结归纳
对顶角相等
对顶角的性质:
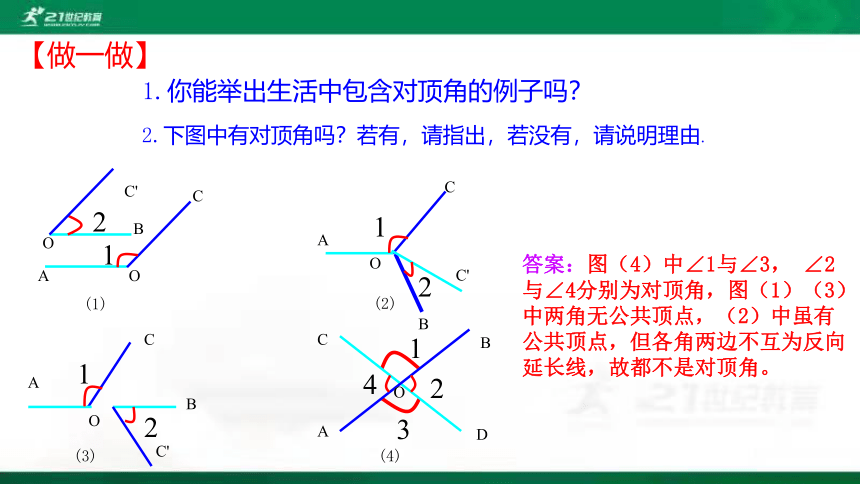
1.你能举出生活中包含对顶角的例子吗?
2.下图中有对顶角吗?若有,请指出,若没有,请说明理由.
B
O
A
O
C
1
2
C'
B
A
C
1
2
C'
A
O
C
1
2
C'
O
(1)
(2)
(3)
B
A
1
3
2
4
B
D
C
O
(4)
【做一做】
答案:图(4)中∠1与∠3, ∠2 与∠4分别为对顶角,图(1)(3)中两角无公共顶点,(2)中虽有公共顶点,但各角两边不互为反向延长线,故都不是对顶角。
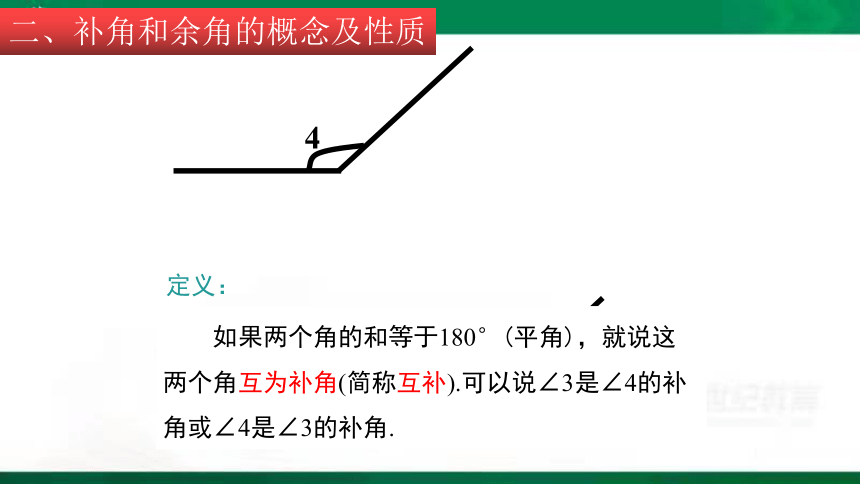
3
4
如果两个角的和等于180°(平角),就说这两个角互为补角(简称互补).可以说∠3是∠4的补角或∠4是∠3的补角.
定义:
二、补角和余角的概念及性质
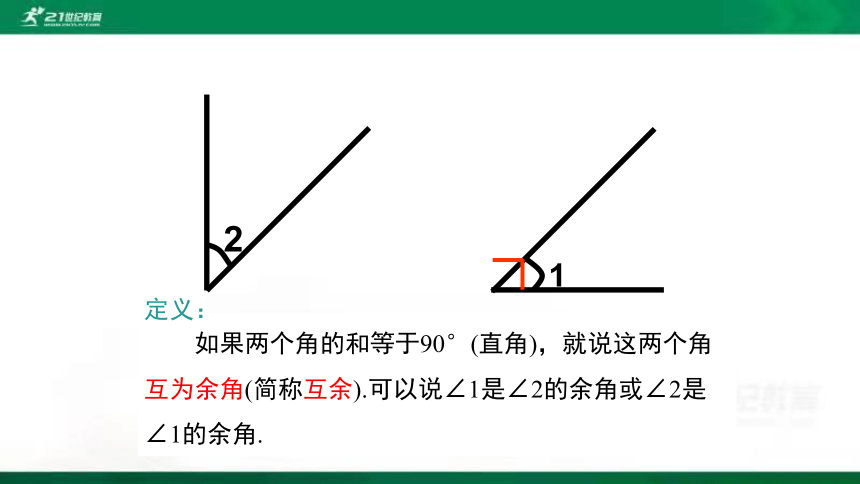
2
1
如果两个角的和等于90°(直角),就说这两个角互为余角(简称互余).可以说∠1是∠2的余角或∠2是∠1的余角.
定义:
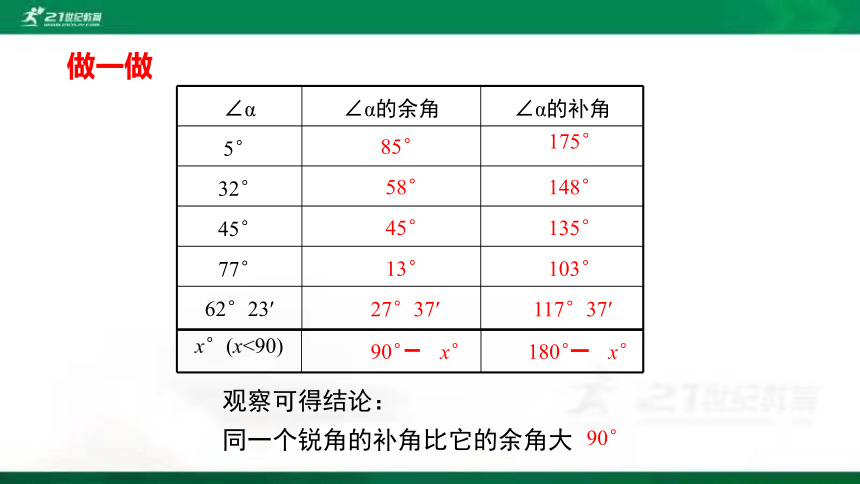
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
x°(x<90)
90° x°
180° x°
观察可得结论:
同一个锐角的补角比它的余角大________.
做一做
90°
图1
N
2
D
C
O
1
3
4
A
B
图2
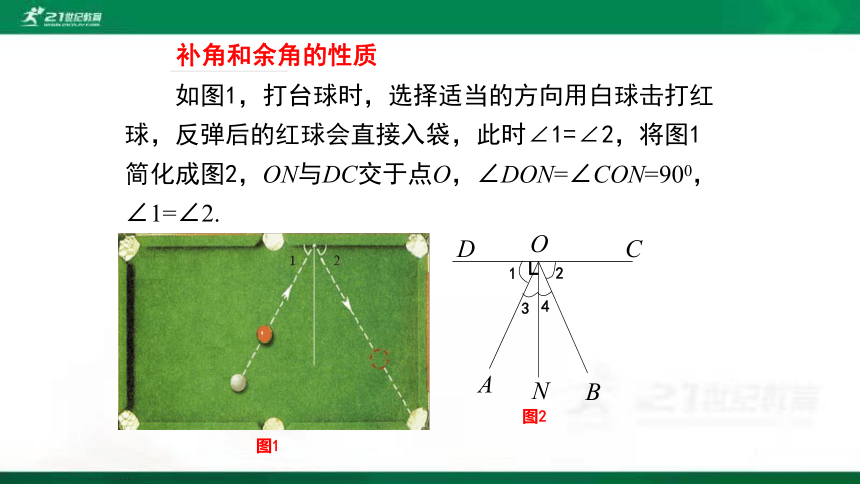
如图1,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图1简化成图2,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2.
补角和余角的性质
小组合作交流,解决下列问题:在图2中
问题1:哪些角互为补角?哪些角互为余角?
问题2:∠3与∠4有什么关系?为什么?
问题3:∠AOC与∠BOD有什么关系?为什么?
因为∠1= ∠2,
∠1+∠AOC=180°,
∠ 2+∠BOD=180°,
所以∠AOC=∠BOD.
同角(等角)的补角相等
N
2
D
C
O
1
3
4
A
B
图2
因为∠1= ∠2,
∠ 1+∠3=90° ,
∠ 2+∠4=90°,
所以 ∠ 3=∠4.
同角(等角)的余角相等
归纳总结:同角(等角)的补角相等,同角(等角)的余角相等.
N
2
D
C
O
1
3
4
A
B
图2
1、一个角的余角等于这个角的补角的 ,求这个角.
分析 用方程解决这个问题要好理解一些,我们可以设这个角为α,列方
程求解.
解析 设这个角为α,依题意得90°-α= ×(180°-α),解得α=67.5°.答:这个角为67.5°.
【做一做】
2、如图2-1-2,点A、O、B在同一直线上,∠AOC=∠EOD=90°.若∠1=35°,则∠2= ,∠3= ,和∠1互余的角是 .
图2-1-2
答案 55°;35°;∠2与∠4
解析 ∵∠AOC=90°,∴∠BOC=180°-∠AOC=90°,
∵∠1=35°,∴∠2=90°-∠1=55°,∵∠EOD=90°,
∴∠3=90°-∠2=90°-55°=35°,∴∠1=∠3.
∵∠3+∠4=90°,∴∠1+∠4=90°,
∴和∠1互余的角为∠2和∠4.
3、一个角的补角是它的余角的10倍,求这个角.
解析 设这个角的大小是x,则180°-x=10(90°-x),解得x=80°.所以这个角为80°.
在相交线的模型中,固定木条a,转动木条b,当b的
位置变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
b
b
)
α
三、垂线及画法
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.
注意:两条线段互相垂直是指这两条线段所在的直线互相垂直.
垂直定义:
知识要点
如果直线AB与直线CD垂直,那么可记作:AB⊥CD(或CD⊥AB).
如果用l、m表示这两条直线,那么直线l与直线m垂直,可记作:l⊥m(或m ⊥ l).
把互相垂直的两条直线的交点叫作垂足(如图中的O点).
A
B
C
D
O
l
m
垂直的表示法
问题:
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能
画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能
画几条
垂线的画法及基本事实
A
.B
l
.
问题:这样画l的垂线可以画几条?
1.放
2.靠
3.画
l
O
如图,已知直线 l,作l的垂线.
A
无数条
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l上的一点A ,作l的垂线.
问题:这样画l的垂线可以画几条?
一条
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点A ,作l的垂线.
根据以上操作,你能得出什么结论
垂线的性质:平面内,过一点有且只有一条直线与已知直线垂直.
注意:
1.“过一点”中的点,可以在已知直线上,也可
以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指
唯一性.
总结归纳
C
D
E
l
1.线段AB, AC, AD , AE谁最短?
2.你能用一句话表示这个结论吗?
说一说:
如图,从A点向已知直线 l 画一条垂直的线段和几条不垂直的线段.
B
A
四、点到直线的距离
连接直线外一点与直线上各点的所有线段中垂线段最短.简单说成:垂线段最短
线段AD的长度叫做点A到直线l的距离.
总结归纳
特别规定:
D
l
A
1.如图2-1-3,OA⊥AB于点A,点O到
直线AB的距离是 ( )
A.线段OA
B.线段OA的长度
C.线段OB的长度
D.线段AB的长度
图2-1-3
答案 B ∵OA⊥AB,∴线段OA即为点O到直线AB的垂线段,根据点到直线的距离的定义可知选B.
【做一做】
2.点P为直线l外的一点,点A,B,C是直线l上的三个点,且PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线l的距离是 ( )
A.2 cm B.小于2 cm
C.不大于2 cm D.4 cm
答案 C 点P到直线l的距离为点P到直线l的垂线段的长度,由垂线段最短,知点P到l的距离小于或等于2 cm,故选C.
3.如图2-1-4,立定跳远比赛时,小明从点A起跳落在沙坑内B处,这次小明
的跳远成绩是4.6米,则小明从起跳点到落脚点之间的距离是 ( )
图2-1-4
A.大于4.6米 B.等于4.6米
C.小于4.6米 D.不能确定
答案 A 跳远的成绩是点B到起跳线的距离,即垂线段的长度为4.6米.结合题图知AB的长大于4.6米.
在同一平面内,两条不重合的直线的位置关系只有两种:相交和平行.
若两条直线只有一个公共点,我们称这两条直线为相交线.在同一平面
内,不相交的两条直线叫做平行线.
如图2-1-1,直线a与直线b平行,记作:a∥b.
如图2-1-2,直线AB与直线CD相交于点O.
图2-1-1 图2-1-2
五、知识点补充:相交线与平行线
1.已知直线AB及一点P,若过点P作一直线与AB平行,则这样的直线 ( )
A.有且只有一条 B.有两条
C.不存在 D.不存在或者只有一条
答案 D 如果P是直线AB外的一点,则只可以作一条;如果P是直线AB上的一点,则不存在.
【做一做】
2.a、b、c是平面内任意三条直线,交点可以有 ( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.都不对
答案 B 分情况讨论:①三条直线平行,此时有0个交点;②只有两条直线平行,此时有2个交点;③三条直线都不平行,此时有1个交点或3个交点.
1.如图,直线AB与直线CD相交于点O,E是∠AOD内一
点,已知OE⊥AB,∠BOD=45°,则∠COE的度数是( )
A.125° B.135° C.145° D.155°
【解析】选B.∠AOC=∠BOD=45°,∠COE=∠AOC+∠AOE=
135°.
课堂练习
2.如图,直线l1与l2相交于点O,
,若 ,则∠β等于( )
A.56° B.46° C.45° D.44°
【解析】选B. 因为∠β的对顶角与∠α互余,所以∠β=90°-∠α=90°-44°=46°.
M
3.如图,点O在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB的大小为( )
A.36° B.54° C.64° D.72°
【解析】选B.因为OC⊥OD,所以∠COD=90°,又因为∠AOB=180°,
所以∠DOB=∠AOB-∠COD-∠COA=180°-90°-36°=54°.
4.点P是直线l外一点,点A,B,C是直线l上三点,且PA=10,PB=8,PC=6,那么点P到直线l的距离为( ).
A.6 B.8
C.大于6的数 D.不大于6的数
【解析】选D.根据“垂线段最短”,垂线段的长度一定小于或等于6,即为不大于6的数.
5.在同一平面内,不重合的两条直线的位置关系可能是 .
6.在同一平面内,两条相交直线公共点的个数是______;两条平行直线的公共点的个数是_____;两条直线重合,公共点有_________个.
相交或平行
1个
0个
无数
7.如图,O为直线AB上一点,∠BOC=26°30′则∠1= .
【解析】由图得∠1与∠BOC互为补角,所以∠1=180°-∠BOC=180°-26°30′=153°30′. 答案:153°30′
8.如图,直线AB,CD相交于点O,OE平分∠AOD,若∠BOD=100°,则∠AOE=_____.
【解析】因为∠AOD+∠BOD=180°,所以∠AOD=180°-100°=80°.因为OE平分∠AOD,所以∠AOE= ∠AOD=40°
答案:40°
一、余角、补角、对顶角的概念:
1. 和为90°的两个角称互为余角;
2. 和为180°的两个角称互为补角;
3. 有公共顶点,且两边互为反向延长线的两个角称为对顶角
1. 同角或等角的余角相等;
2. 同角或等角的补角相等;
3. 对顶角相等.
课堂小结
二、余角、补角、对顶角的性质:
1.垂直定义;
2.垂直的画法;
3.垂直的记法;
4.垂直的一个结论;
5.点到直线的距离.
三、垂直的相关知识:
四、两条直线的位置关系
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第二章 平行线与相交线
2.1 两条直线的位置关系
北师大版 七年级下册数学
观察下列图片,说一说直线与直线的位置关系.
情景引入
生活中处处可见道路、房屋、山川、桥梁.在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线.
在同一平面内,两条直线的位置关系有相交和平行两种.若两条直线只有一个公共点,我们称这两条直线为相交线.在同一平面内,不相交的两条直线叫作平行线.
如图,直线AB、CD相交于O,∠1和∠2有什么位置关系?
2
1
A
B
C
D
O
3
4
探究一:
1.有公共顶点,
2.两边互为反向延长线.
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角.
一、对顶角的概念及性质
请你观察图中∠1和∠2这组对顶角,你发现它们的大小有什么关系
2
1
A
B
C
D
O
探究二:
∠1=∠2
对顶角相等
如图直线AB与CD相交于点O,∠1和∠3有公共顶点O,并且它们的两边互为反向延长线,这样的两个角叫做对顶角.∠2和∠4也是对顶角.
对顶角:
A
O
C
B
D
1
3
2
4
总结归纳
对顶角相等
对顶角的性质:
1.你能举出生活中包含对顶角的例子吗?
2.下图中有对顶角吗?若有,请指出,若没有,请说明理由.
B
O
A
O
C
1
2
C'
B
A
C
1
2
C'
A
O
C
1
2
C'
O
(1)
(2)
(3)
B
A
1
3
2
4
B
D
C
O
(4)
【做一做】
答案:图(4)中∠1与∠3, ∠2 与∠4分别为对顶角,图(1)(3)中两角无公共顶点,(2)中虽有公共顶点,但各角两边不互为反向延长线,故都不是对顶角。
3
4
如果两个角的和等于180°(平角),就说这两个角互为补角(简称互补).可以说∠3是∠4的补角或∠4是∠3的补角.
定义:
二、补角和余角的概念及性质
2
1
如果两个角的和等于90°(直角),就说这两个角互为余角(简称互余).可以说∠1是∠2的余角或∠2是∠1的余角.
定义:
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
x°(x<90)
90° x°
180° x°
观察可得结论:
同一个锐角的补角比它的余角大________.
做一做
90°
图1
N
2
D
C
O
1
3
4
A
B
图2
如图1,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图1简化成图2,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2.
补角和余角的性质
小组合作交流,解决下列问题:在图2中
问题1:哪些角互为补角?哪些角互为余角?
问题2:∠3与∠4有什么关系?为什么?
问题3:∠AOC与∠BOD有什么关系?为什么?
因为∠1= ∠2,
∠1+∠AOC=180°,
∠ 2+∠BOD=180°,
所以∠AOC=∠BOD.
同角(等角)的补角相等
N
2
D
C
O
1
3
4
A
B
图2
因为∠1= ∠2,
∠ 1+∠3=90° ,
∠ 2+∠4=90°,
所以 ∠ 3=∠4.
同角(等角)的余角相等
归纳总结:同角(等角)的补角相等,同角(等角)的余角相等.
N
2
D
C
O
1
3
4
A
B
图2
1、一个角的余角等于这个角的补角的 ,求这个角.
分析 用方程解决这个问题要好理解一些,我们可以设这个角为α,列方
程求解.
解析 设这个角为α,依题意得90°-α= ×(180°-α),解得α=67.5°.答:这个角为67.5°.
【做一做】
2、如图2-1-2,点A、O、B在同一直线上,∠AOC=∠EOD=90°.若∠1=35°,则∠2= ,∠3= ,和∠1互余的角是 .
图2-1-2
答案 55°;35°;∠2与∠4
解析 ∵∠AOC=90°,∴∠BOC=180°-∠AOC=90°,
∵∠1=35°,∴∠2=90°-∠1=55°,∵∠EOD=90°,
∴∠3=90°-∠2=90°-55°=35°,∴∠1=∠3.
∵∠3+∠4=90°,∴∠1+∠4=90°,
∴和∠1互余的角为∠2和∠4.
3、一个角的补角是它的余角的10倍,求这个角.
解析 设这个角的大小是x,则180°-x=10(90°-x),解得x=80°.所以这个角为80°.
在相交线的模型中,固定木条a,转动木条b,当b的
位置变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
b
b
)
α
三、垂线及画法
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.
注意:两条线段互相垂直是指这两条线段所在的直线互相垂直.
垂直定义:
知识要点
如果直线AB与直线CD垂直,那么可记作:AB⊥CD(或CD⊥AB).
如果用l、m表示这两条直线,那么直线l与直线m垂直,可记作:l⊥m(或m ⊥ l).
把互相垂直的两条直线的交点叫作垂足(如图中的O点).
A
B
C
D
O
l
m
垂直的表示法
问题:
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能
画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能
画几条
垂线的画法及基本事实
A
.B
l
.
问题:这样画l的垂线可以画几条?
1.放
2.靠
3.画
l
O
如图,已知直线 l,作l的垂线.
A
无数条
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l上的一点A ,作l的垂线.
问题:这样画l的垂线可以画几条?
一条
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点A ,作l的垂线.
根据以上操作,你能得出什么结论
垂线的性质:平面内,过一点有且只有一条直线与已知直线垂直.
注意:
1.“过一点”中的点,可以在已知直线上,也可
以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指
唯一性.
总结归纳
C
D
E
l
1.线段AB, AC, AD , AE谁最短?
2.你能用一句话表示这个结论吗?
说一说:
如图,从A点向已知直线 l 画一条垂直的线段和几条不垂直的线段.
B
A
四、点到直线的距离
连接直线外一点与直线上各点的所有线段中垂线段最短.简单说成:垂线段最短
线段AD的长度叫做点A到直线l的距离.
总结归纳
特别规定:
D
l
A
1.如图2-1-3,OA⊥AB于点A,点O到
直线AB的距离是 ( )
A.线段OA
B.线段OA的长度
C.线段OB的长度
D.线段AB的长度
图2-1-3
答案 B ∵OA⊥AB,∴线段OA即为点O到直线AB的垂线段,根据点到直线的距离的定义可知选B.
【做一做】
2.点P为直线l外的一点,点A,B,C是直线l上的三个点,且PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线l的距离是 ( )
A.2 cm B.小于2 cm
C.不大于2 cm D.4 cm
答案 C 点P到直线l的距离为点P到直线l的垂线段的长度,由垂线段最短,知点P到l的距离小于或等于2 cm,故选C.
3.如图2-1-4,立定跳远比赛时,小明从点A起跳落在沙坑内B处,这次小明
的跳远成绩是4.6米,则小明从起跳点到落脚点之间的距离是 ( )
图2-1-4
A.大于4.6米 B.等于4.6米
C.小于4.6米 D.不能确定
答案 A 跳远的成绩是点B到起跳线的距离,即垂线段的长度为4.6米.结合题图知AB的长大于4.6米.
在同一平面内,两条不重合的直线的位置关系只有两种:相交和平行.
若两条直线只有一个公共点,我们称这两条直线为相交线.在同一平面
内,不相交的两条直线叫做平行线.
如图2-1-1,直线a与直线b平行,记作:a∥b.
如图2-1-2,直线AB与直线CD相交于点O.
图2-1-1 图2-1-2
五、知识点补充:相交线与平行线
1.已知直线AB及一点P,若过点P作一直线与AB平行,则这样的直线 ( )
A.有且只有一条 B.有两条
C.不存在 D.不存在或者只有一条
答案 D 如果P是直线AB外的一点,则只可以作一条;如果P是直线AB上的一点,则不存在.
【做一做】
2.a、b、c是平面内任意三条直线,交点可以有 ( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.都不对
答案 B 分情况讨论:①三条直线平行,此时有0个交点;②只有两条直线平行,此时有2个交点;③三条直线都不平行,此时有1个交点或3个交点.
1.如图,直线AB与直线CD相交于点O,E是∠AOD内一
点,已知OE⊥AB,∠BOD=45°,则∠COE的度数是( )
A.125° B.135° C.145° D.155°
【解析】选B.∠AOC=∠BOD=45°,∠COE=∠AOC+∠AOE=
135°.
课堂练习
2.如图,直线l1与l2相交于点O,
,若 ,则∠β等于( )
A.56° B.46° C.45° D.44°
【解析】选B. 因为∠β的对顶角与∠α互余,所以∠β=90°-∠α=90°-44°=46°.
M
3.如图,点O在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB的大小为( )
A.36° B.54° C.64° D.72°
【解析】选B.因为OC⊥OD,所以∠COD=90°,又因为∠AOB=180°,
所以∠DOB=∠AOB-∠COD-∠COA=180°-90°-36°=54°.
4.点P是直线l外一点,点A,B,C是直线l上三点,且PA=10,PB=8,PC=6,那么点P到直线l的距离为( ).
A.6 B.8
C.大于6的数 D.不大于6的数
【解析】选D.根据“垂线段最短”,垂线段的长度一定小于或等于6,即为不大于6的数.
5.在同一平面内,不重合的两条直线的位置关系可能是 .
6.在同一平面内,两条相交直线公共点的个数是______;两条平行直线的公共点的个数是_____;两条直线重合,公共点有_________个.
相交或平行
1个
0个
无数
7.如图,O为直线AB上一点,∠BOC=26°30′则∠1= .
【解析】由图得∠1与∠BOC互为补角,所以∠1=180°-∠BOC=180°-26°30′=153°30′. 答案:153°30′
8.如图,直线AB,CD相交于点O,OE平分∠AOD,若∠BOD=100°,则∠AOE=_____.
【解析】因为∠AOD+∠BOD=180°,所以∠AOD=180°-100°=80°.因为OE平分∠AOD,所以∠AOE= ∠AOD=40°
答案:40°
一、余角、补角、对顶角的概念:
1. 和为90°的两个角称互为余角;
2. 和为180°的两个角称互为补角;
3. 有公共顶点,且两边互为反向延长线的两个角称为对顶角
1. 同角或等角的余角相等;
2. 同角或等角的补角相等;
3. 对顶角相等.
课堂小结
二、余角、补角、对顶角的性质:
1.垂直定义;
2.垂直的画法;
3.垂直的记法;
4.垂直的一个结论;
5.点到直线的距离.
三、垂直的相关知识:
四、两条直线的位置关系
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
