2021-2022学年七年级数学苏科版下册7.3图形的平移 同步习题(word版含解析)
文档属性
| 名称 | 2021-2022学年七年级数学苏科版下册7.3图形的平移 同步习题(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 315.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-31 20:01:56 | ||
图片预览




文档简介
7.3图形的平移
一、选择题
1.如图,将周长为的三角形沿边向右平移个单位长度,得到三角形,则四边形的周长为
A. B. C. D.
第1题 第2题
2.如图,是经过平移得到的,则平移的方向是
A. 射线的方向 B. 射线的方向
C. 射线的方向 D. 无法确定
3.如图是一块长方形的场地,长,宽,、两处入口的路宽为,两小路汇合处路宽为,其余部分种植草坪,则草坪面积为
A. B. C. D.
第3 题 第4题 第5题
4.如图,将三角形沿直线平移得到三角形,其中,点和点是对应点,点和点是对应点,点和点是对应点.如果,,那么线段的长是
A. B. . D.
5.如图,沿方向向右平移后到达的位置,与相交于点,若的度数为,则的度数为
A. B. C. D.
二、填空题
6.如图,将面积为的三角形沿方向平移至三角形的位置,平移的距离是边长的倍,那么图中线段与的关系是 ,四边形的面积为 .
第6 题 第7题 第8题
7.如图,将直角沿着点到点的方向平移到的位置,平移距离为,若,,则阴影部分面积为______________.
8.如图,将沿方向平移得到,若的周长为,则四边形的周长为______.
9.如图,,,、在上,且满足,平分,若平行移动,当的度数为______时,可以使.
第9题 第10题 第11题
10.大正方形的边长为厘米,小正方形的边长为厘米,起始状态如图所示.大正方形固定不动,把小正方形以厘米秒的速度向右沿直线平移,设平移的时间为秒,两个正方形重叠部分的面积为平方厘米.当时,小正方形平移的时间_________秒.
11.如图,在中,,将沿着射线方向平移到,连结若和这两个角中,有一个角是另一个角的倍,则_________度
三、解答题
12.以下现象属于平移的是 .
足球在草地上滚动钟摆的摆动
传送带上,瓶装饮料的移动.
13.画图并填空:
如图,画出中边上的高标出点的位置;
画出把沿射线方向平移后得到的;
根据“图形平移”的性质,得______,线段与线段的关系是:______.
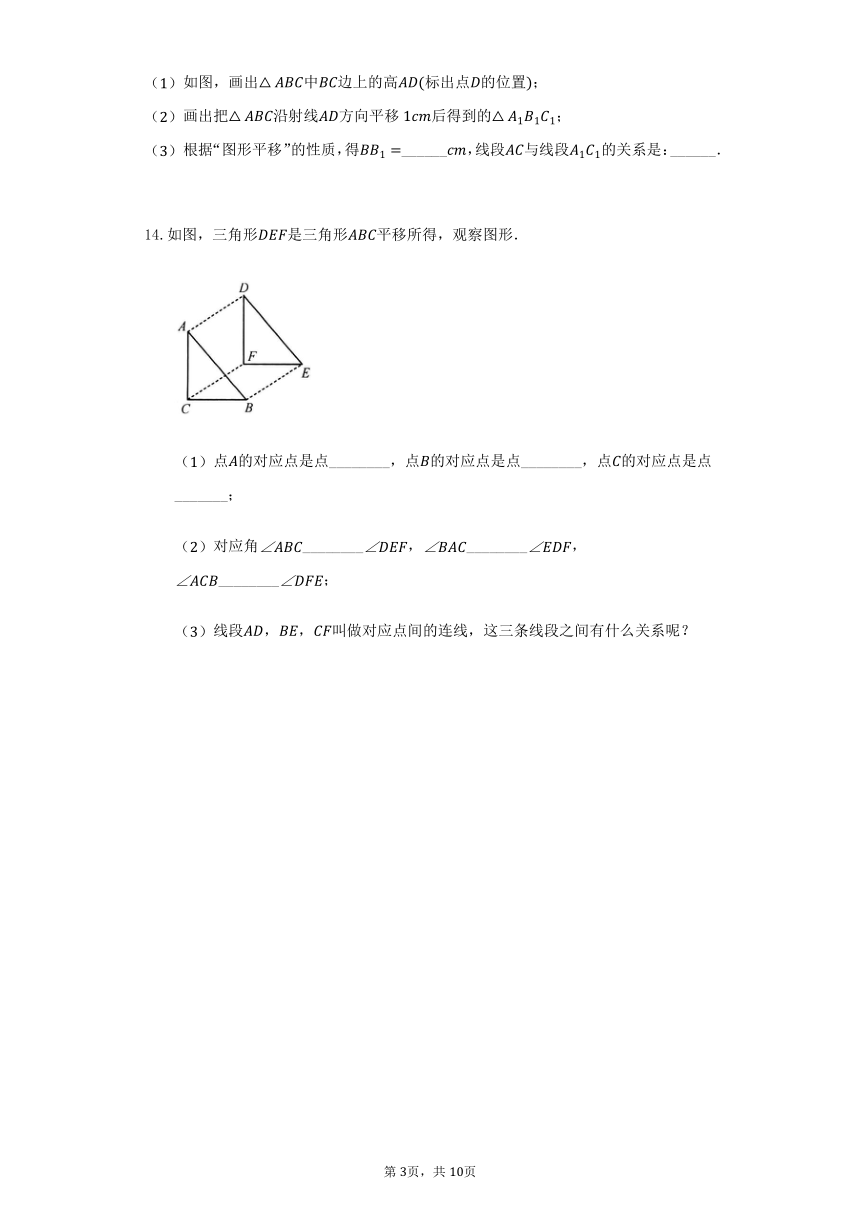
14.如图,三角形是三角形平移所得,观察图形.
点的对应点是点________,点的对应点是点________,点的对应点是点_______;
对应角________,________,________;
线段,,叫做对应点间的连线,这三条线段之间有什么关系呢?
1.【答案】
【解析】解:根据平移变换的性质,选项C符合题意.
故选:.
根据平移变换的性质作出图形即可.
本题考查作图平移变换,解题的关键是掌握平移变换的性质,属于中考常考题型.
2.【答案】
【解析】解:沿边向右平移个单位,得到,
,,
的周长为,
,
,
四边形的周长.
故答案为.
3.【答案】
【解析】
【分析】
本题主要考查了平移的方向问题.注意平移是沿某一直线移动的,其移动的方向是沿对应点连接的射线的方向移动.图形平移的方向是连接对应点的射线的方向.
【解答】
解:是经过平移得到的,且点和点是对应点,
平移的方向是射线的方向.
故选B.
4.【答案】
【解析】
【分析】
此题考查了生活中的平移,根据图形得出草坪正好可以拼成一个长方形是解题关键.根据已知将道路平移,再利用矩形的性质求出长和宽,再进行解答.
【解答】
解:由图可知:矩形中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:米,宽为米.
所以草坪的面积应该是长宽米
故选A.
5.【答案】
【解析】解:由平移的性质可知,,
,,
,
,
故选:.
由平移的性质可知,,求出即可解决问题.
本题考查平移的性质,线段的和差定义等知识,解题的关键是掌握平移变换的性质,属于中考常考题型.
6.【答案】
【解析】解:沿方向向右平移后到达的位置,与相交于点,
,,
,
,
故选:.
根据平移的性质得出,,
本题考查了平移的性质,熟记平移的性质:平移变换只改变图形的位置不改变图形的形状是解题的关键.
7.【答案】平行且相等
【解析】解:设点到的距离为,
则三角形的面积为.
因为平移的距离是边长的倍,
所以,.
所以四边形的面积为.
8.【答案】
【解析】
【分析】
本题主要考查了平移的性质及梯形的面积公式,得出阴影部分和梯形的面积相等是解题的关键.根据平移的性质得出,,则,则阴影部分面积,根据梯形的面积公式即可求解.
【解答】
解:由平移的性质知,,,
,
.
故答案为.
9.【答案】
【解析】解:沿方向平移得到,
,,
四边形的周长,
的周长,
,
四边形的周长.
故答案为:.
据平移的性质可得,,然后根据四边形的周长的定义列式计算即可得解.
本题考查了平移的性质,熟记性质得到相等的线段是解题的关键.
10.【答案】
【解析】解:,
,
,
,平分,
;
在平行移动的过程中,存在,
设,,
,
,
,,
,
,.
即:当度时.可以使.
故答案为:.
由于,,易求,而、都是角平分线,从而可求;设,,根据三角形的外角性质、三角形的内角和定理、平行线的性质可得,,,解即可.
本题考查了平行线的性质、角平分线的定义及平移的性质,两直线平行时,应该想到它们的性质,由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.
11.【答案】或
【解析】
【分析】
本题考查了平移的性质,主要利用了长方形的面积,难点在于分两种情况解答.
先求出重叠部分长方形的宽,再分重叠部分在大正方形的左边和右边两种情况讨论求解.
【解答】
解:当时,重叠部分长方形的宽,
重叠部分在大正方形的左边时,秒,
重叠部分在大正方形的右边时,秒,
综上所述,小正方形平移的时间为或秒.
故答案为或.
12.【答案】或或
【解析】
【分析】
本题主要考查了平行线的性质、平移的性质、分类讨论思想的知识点,解题关键点是熟练掌握平行线的性质分点在之间和点在延长线上两种情况进行分别讨论,即可解答.
【解答】
解:如图,当点在之间时,
将沿着射线方向平移得到,
,,,
,
,
,
当时,,解得:,
当时,,解得:,
即;
如图,当点在延长线上时,
将沿着射线方向平移得到,
,,
,
,
,
当时,,
解得:,
当时,,无解,
综上所述,的度数为或或.
故答案为或或.
13.【答案】略
【解析】略
14.【答案】 平行且相等
【解析】解:
;
;
,平行且相等.分
从点向的延长线作垂线段即可;
过、分别做的平行线,并且在平行线上截取,连接,,,得到的即为平移后的新图形;
利用平移的性质:对应线段平行且相等,对应点的连线平行且相等即可求解.
解答此题的关键是掌握平移的性质,平移作图的步骤,三角形高线的作法.
15.【答案】解:
,.
【解析】略
第2页,共2页
第1页,共1页
一、选择题
1.如图,将周长为的三角形沿边向右平移个单位长度,得到三角形,则四边形的周长为
A. B. C. D.
第1题 第2题
2.如图,是经过平移得到的,则平移的方向是
A. 射线的方向 B. 射线的方向
C. 射线的方向 D. 无法确定
3.如图是一块长方形的场地,长,宽,、两处入口的路宽为,两小路汇合处路宽为,其余部分种植草坪,则草坪面积为
A. B. C. D.
第3 题 第4题 第5题
4.如图,将三角形沿直线平移得到三角形,其中,点和点是对应点,点和点是对应点,点和点是对应点.如果,,那么线段的长是
A. B. . D.
5.如图,沿方向向右平移后到达的位置,与相交于点,若的度数为,则的度数为
A. B. C. D.
二、填空题
6.如图,将面积为的三角形沿方向平移至三角形的位置,平移的距离是边长的倍,那么图中线段与的关系是 ,四边形的面积为 .
第6 题 第7题 第8题
7.如图,将直角沿着点到点的方向平移到的位置,平移距离为,若,,则阴影部分面积为______________.
8.如图,将沿方向平移得到,若的周长为,则四边形的周长为______.
9.如图,,,、在上,且满足,平分,若平行移动,当的度数为______时,可以使.
第9题 第10题 第11题
10.大正方形的边长为厘米,小正方形的边长为厘米,起始状态如图所示.大正方形固定不动,把小正方形以厘米秒的速度向右沿直线平移,设平移的时间为秒,两个正方形重叠部分的面积为平方厘米.当时,小正方形平移的时间_________秒.
11.如图,在中,,将沿着射线方向平移到,连结若和这两个角中,有一个角是另一个角的倍,则_________度
三、解答题
12.以下现象属于平移的是 .
足球在草地上滚动钟摆的摆动
传送带上,瓶装饮料的移动.
13.画图并填空:
如图,画出中边上的高标出点的位置;
画出把沿射线方向平移后得到的;
根据“图形平移”的性质,得______,线段与线段的关系是:______.
14.如图,三角形是三角形平移所得,观察图形.
点的对应点是点________,点的对应点是点________,点的对应点是点_______;
对应角________,________,________;
线段,,叫做对应点间的连线,这三条线段之间有什么关系呢?
1.【答案】
【解析】解:根据平移变换的性质,选项C符合题意.
故选:.
根据平移变换的性质作出图形即可.
本题考查作图平移变换,解题的关键是掌握平移变换的性质,属于中考常考题型.
2.【答案】
【解析】解:沿边向右平移个单位,得到,
,,
的周长为,
,
,
四边形的周长.
故答案为.
3.【答案】
【解析】
【分析】
本题主要考查了平移的方向问题.注意平移是沿某一直线移动的,其移动的方向是沿对应点连接的射线的方向移动.图形平移的方向是连接对应点的射线的方向.
【解答】
解:是经过平移得到的,且点和点是对应点,
平移的方向是射线的方向.
故选B.
4.【答案】
【解析】
【分析】
此题考查了生活中的平移,根据图形得出草坪正好可以拼成一个长方形是解题关键.根据已知将道路平移,再利用矩形的性质求出长和宽,再进行解答.
【解答】
解:由图可知:矩形中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:米,宽为米.
所以草坪的面积应该是长宽米
故选A.
5.【答案】
【解析】解:由平移的性质可知,,
,,
,
,
故选:.
由平移的性质可知,,求出即可解决问题.
本题考查平移的性质,线段的和差定义等知识,解题的关键是掌握平移变换的性质,属于中考常考题型.
6.【答案】
【解析】解:沿方向向右平移后到达的位置,与相交于点,
,,
,
,
故选:.
根据平移的性质得出,,
本题考查了平移的性质,熟记平移的性质:平移变换只改变图形的位置不改变图形的形状是解题的关键.
7.【答案】平行且相等
【解析】解:设点到的距离为,
则三角形的面积为.
因为平移的距离是边长的倍,
所以,.
所以四边形的面积为.
8.【答案】
【解析】
【分析】
本题主要考查了平移的性质及梯形的面积公式,得出阴影部分和梯形的面积相等是解题的关键.根据平移的性质得出,,则,则阴影部分面积,根据梯形的面积公式即可求解.
【解答】
解:由平移的性质知,,,
,
.
故答案为.
9.【答案】
【解析】解:沿方向平移得到,
,,
四边形的周长,
的周长,
,
四边形的周长.
故答案为:.
据平移的性质可得,,然后根据四边形的周长的定义列式计算即可得解.
本题考查了平移的性质,熟记性质得到相等的线段是解题的关键.
10.【答案】
【解析】解:,
,
,
,平分,
;
在平行移动的过程中,存在,
设,,
,
,
,,
,
,.
即:当度时.可以使.
故答案为:.
由于,,易求,而、都是角平分线,从而可求;设,,根据三角形的外角性质、三角形的内角和定理、平行线的性质可得,,,解即可.
本题考查了平行线的性质、角平分线的定义及平移的性质,两直线平行时,应该想到它们的性质,由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.
11.【答案】或
【解析】
【分析】
本题考查了平移的性质,主要利用了长方形的面积,难点在于分两种情况解答.
先求出重叠部分长方形的宽,再分重叠部分在大正方形的左边和右边两种情况讨论求解.
【解答】
解:当时,重叠部分长方形的宽,
重叠部分在大正方形的左边时,秒,
重叠部分在大正方形的右边时,秒,
综上所述,小正方形平移的时间为或秒.
故答案为或.
12.【答案】或或
【解析】
【分析】
本题主要考查了平行线的性质、平移的性质、分类讨论思想的知识点,解题关键点是熟练掌握平行线的性质分点在之间和点在延长线上两种情况进行分别讨论,即可解答.
【解答】
解:如图,当点在之间时,
将沿着射线方向平移得到,
,,,
,
,
,
当时,,解得:,
当时,,解得:,
即;
如图,当点在延长线上时,
将沿着射线方向平移得到,
,,
,
,
,
当时,,
解得:,
当时,,无解,
综上所述,的度数为或或.
故答案为或或.
13.【答案】略
【解析】略
14.【答案】 平行且相等
【解析】解:
;
;
,平行且相等.分
从点向的延长线作垂线段即可;
过、分别做的平行线,并且在平行线上截取,连接,,,得到的即为平移后的新图形;
利用平移的性质:对应线段平行且相等,对应点的连线平行且相等即可求解.
解答此题的关键是掌握平移的性质,平移作图的步骤,三角形高线的作法.
15.【答案】解:
,.
【解析】略
第2页,共2页
第1页,共1页
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
