2021-2022学年人教版七年级数学下册5.4 平移 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.4 平移 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 645.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-01 16:45:59 | ||
图片预览





文档简介
(共20张PPT)
5.4 平移(1)
5
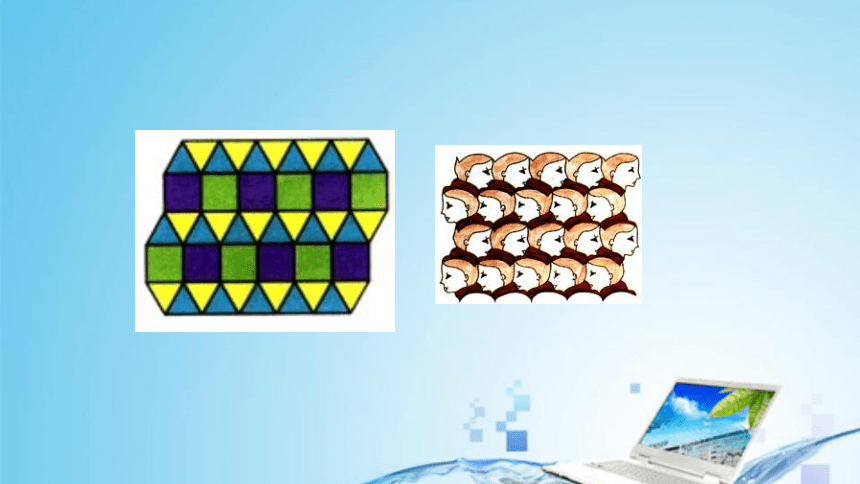
图片欣赏
你知道这几幅图案中的运动的现象有什么共同的特点吗?
讨论与交流
如何在一张纸上画出一排和书上第
30页图5.4-2形状、大小都一样的雪人
三思而行,请先分组讨
论一下!动手画一画,你就
是未来的大画家!
你画的雪人和书上的
一样吗?你是怎么画的?
可以把一张半透明的纸盖在图5.4-2上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个……(如图5.4-3)
雪人的大小和形状改变了吗? 位置呢?
雪人甲
雪人乙
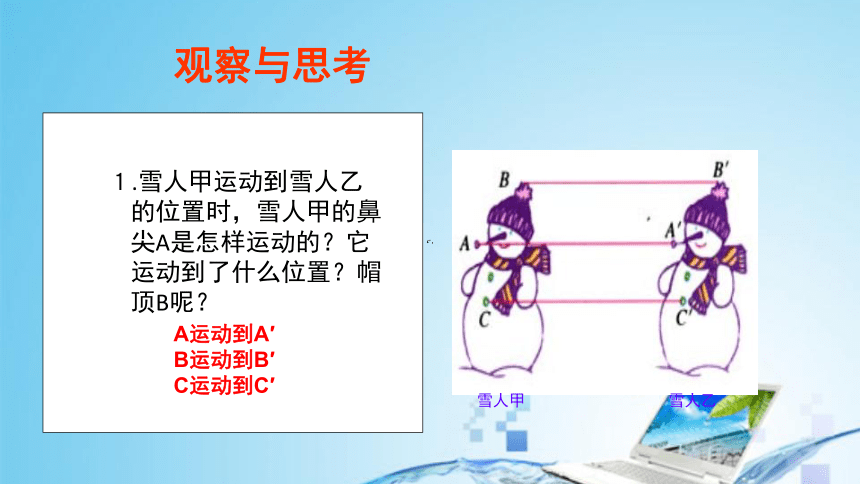
观察与思考
1.雪人甲运动到雪人乙的位置时,雪人甲的鼻尖A是怎样运动的?它运动到了什么位置?帽顶B呢?
A运动到A′
B运动到B′
C运动到C′
可以发现:AA′∥BB′∥CC′, 并且AA′=BB′= CC′
请你连接其他对应点的线段,它们是否仍有前面的关系?
有
平移的定义:一个图形沿着某个方向移动一定的距离,图形的这种移动,叫做平移变换,简称平移。
平移特征:
1 . 把一个图形整体沿某一个方向移动,会得到一个新的图形.新图形与原图形的形状和大小完全相同.
2.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点就是对应点。连接各组对应点的线段平行且相等
简单的说:
(1)平移不改变图形的形状和大小;
(2)对应点连线平行且相等.
想一想
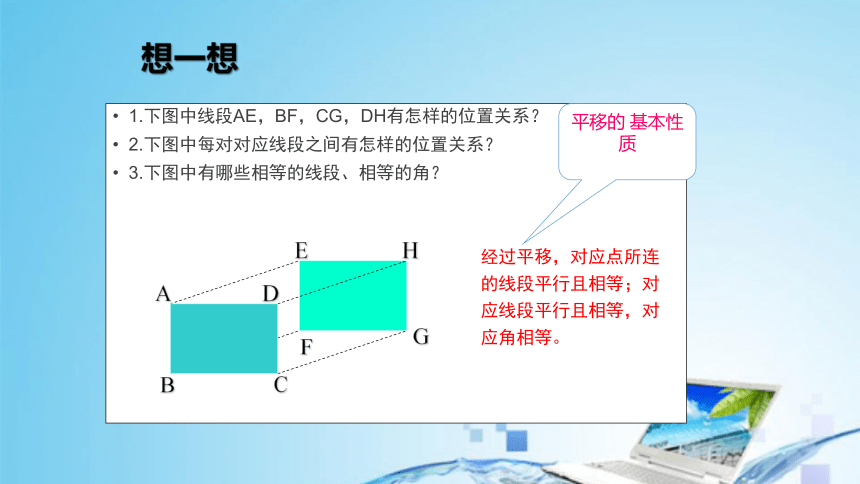
1.下图中线段AE,BF,CG,DH有怎样的位置关系?
2.下图中每对对应线段之间有怎样的位置关系?
3.下图中有哪些相等的线段、相等的角?
经过平移,对应点所连的线段平行且相等;对应线段平行且相等,对应角相等。
平移的 基本性质
E
F
G
H
A
C
B
D
课堂练习
在下面的六幅图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到?
√
下面 2,3,4,5 幅图中哪幅图是由1平移得到的?
1
2
3
4
5
(1)
(2)
2
3
4
5
1
√
√
例1:如图,平移线段AB,使点A移动到点A′.画出平移后的线段A′B′
A
B
A′
B′
分析:“点A移到点A′”这句话告诉我们图形平移的方向是A到A′的方向, 平移的距离为线段AA′的长,根据这两个要素就可以确定点B′.
解:如图,过B′点做AA′的平行线L,在直线L上截取BB ′=AA′,连接A′B′,则线段A′B′就是所求画的线段。
L
平移线段画法
平移三角形的作法
例 2: 经过平移,三角形ABC的顶点A移到了点 D. 画出平移后的三角形.
A
B
C
分析:设顶点 B,C分别平移 到了E,F,
E
F
D
解:如图,过 B,C点分别做线段BE,CF使得他们与线段AD平行且相等,连接 DE,DF,EF。 三角形 DEF 就是三角形ABC平移后的图形.
根据“经过平移,对应点所连的线段平行且相等”,可知线段 BE,CF与AD平行且相等.
生活中的平移
例题3:如下图△ABE沿射线XY的方向平移一定距离后成为△CDF. 找出图中存在的平行且相等的三条线段。
Y
X
E
B
A
C
D
F
解:点A,B,E的对应点分别为
点C,D,F,因为经过平移, 对应点所连的线段平行且相等 , 所以AC∥BD ∥ EF,且AC=BD=EF.
生活中的平移
练习一
A
B
C
F
G
E
如下图△EFG是将△ABC沿箭头方向平移一定距离而得. 试找出图中平行且相等的线段。
练习二
如下图∠ ABC 是∠O经过平移而得的角,若∠O=65°,则∠ABC等于多少度?
A
B
C
O
D
① ② ③ ④
⑤ ⑥ ⑦ ⑧
练习三
在下面的八幅图案中,②③④⑤⑥⑦⑧中的哪个图案可以通过平移图案①得到?
A
C
B
练习四
由△ABC平移而得的三角形共有多少个?
解:
共有5个。
练习五
能由△AOB平移而得的图形是哪个?
D
A
B
C
D
E
F
o
解:
能由△AOB平移
而得的图形是:△FOE, △COD
生活中的平移
平移的定义
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
平移的性质
平移不改变图形的形状和大小。经过平移,对应点所连的线段平行且相等;对应线段平行且相等,对应角相等。
本课小结
5.4 平移(1)
5
图片欣赏
你知道这几幅图案中的运动的现象有什么共同的特点吗?
讨论与交流
如何在一张纸上画出一排和书上第
30页图5.4-2形状、大小都一样的雪人
三思而行,请先分组讨
论一下!动手画一画,你就
是未来的大画家!
你画的雪人和书上的
一样吗?你是怎么画的?
可以把一张半透明的纸盖在图5.4-2上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个……(如图5.4-3)
雪人的大小和形状改变了吗? 位置呢?
雪人甲
雪人乙
观察与思考
1.雪人甲运动到雪人乙的位置时,雪人甲的鼻尖A是怎样运动的?它运动到了什么位置?帽顶B呢?
A运动到A′
B运动到B′
C运动到C′
可以发现:AA′∥BB′∥CC′, 并且AA′=BB′= CC′
请你连接其他对应点的线段,它们是否仍有前面的关系?
有
平移的定义:一个图形沿着某个方向移动一定的距离,图形的这种移动,叫做平移变换,简称平移。
平移特征:
1 . 把一个图形整体沿某一个方向移动,会得到一个新的图形.新图形与原图形的形状和大小完全相同.
2.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点就是对应点。连接各组对应点的线段平行且相等
简单的说:
(1)平移不改变图形的形状和大小;
(2)对应点连线平行且相等.
想一想
1.下图中线段AE,BF,CG,DH有怎样的位置关系?
2.下图中每对对应线段之间有怎样的位置关系?
3.下图中有哪些相等的线段、相等的角?
经过平移,对应点所连的线段平行且相等;对应线段平行且相等,对应角相等。
平移的 基本性质
E
F
G
H
A
C
B
D
课堂练习
在下面的六幅图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到?
√
下面 2,3,4,5 幅图中哪幅图是由1平移得到的?
1
2
3
4
5
(1)
(2)
2
3
4
5
1
√
√
例1:如图,平移线段AB,使点A移动到点A′.画出平移后的线段A′B′
A
B
A′
B′
分析:“点A移到点A′”这句话告诉我们图形平移的方向是A到A′的方向, 平移的距离为线段AA′的长,根据这两个要素就可以确定点B′.
解:如图,过B′点做AA′的平行线L,在直线L上截取BB ′=AA′,连接A′B′,则线段A′B′就是所求画的线段。
L
平移线段画法
平移三角形的作法
例 2: 经过平移,三角形ABC的顶点A移到了点 D. 画出平移后的三角形.
A
B
C
分析:设顶点 B,C分别平移 到了E,F,
E
F
D
解:如图,过 B,C点分别做线段BE,CF使得他们与线段AD平行且相等,连接 DE,DF,EF。 三角形 DEF 就是三角形ABC平移后的图形.
根据“经过平移,对应点所连的线段平行且相等”,可知线段 BE,CF与AD平行且相等.
生活中的平移
例题3:如下图△ABE沿射线XY的方向平移一定距离后成为△CDF. 找出图中存在的平行且相等的三条线段。
Y
X
E
B
A
C
D
F
解:点A,B,E的对应点分别为
点C,D,F,因为经过平移, 对应点所连的线段平行且相等 , 所以AC∥BD ∥ EF,且AC=BD=EF.
生活中的平移
练习一
A
B
C
F
G
E
如下图△EFG是将△ABC沿箭头方向平移一定距离而得. 试找出图中平行且相等的线段。
练习二
如下图∠ ABC 是∠O经过平移而得的角,若∠O=65°,则∠ABC等于多少度?
A
B
C
O
D
① ② ③ ④
⑤ ⑥ ⑦ ⑧
练习三
在下面的八幅图案中,②③④⑤⑥⑦⑧中的哪个图案可以通过平移图案①得到?
A
C
B
练习四
由△ABC平移而得的三角形共有多少个?
解:
共有5个。
练习五
能由△AOB平移而得的图形是哪个?
D
A
B
C
D
E
F
o
解:
能由△AOB平移
而得的图形是:△FOE, △COD
生活中的平移
平移的定义
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
平移的性质
平移不改变图形的形状和大小。经过平移,对应点所连的线段平行且相等;对应线段平行且相等,对应角相等。
本课小结
