西师大版 六年级下册数学-3.2 正比例 课件(共15张PPT)
文档属性
| 名称 | 西师大版 六年级下册数学-3.2 正比例 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 761.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 19:19:19 | ||
图片预览




文档简介
(共15张PPT)
1.正比例
R·六年级下册
已知路程和时间,怎样求速度?
速度 = 路程÷时间
已知总价和数量,怎样求单价?
单价 = 总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作效率 = 工作总量÷工作时间
新课导入
下面是正方形的边长与周长的变化.
把表填完整.
边长/cm 周长/cm
1 4
0
2
4
6
8
10
12
1
2
3
4
边长/cm
周长/cm
14
16
2
8
3
12
4
16
观察数据,你有什么发现
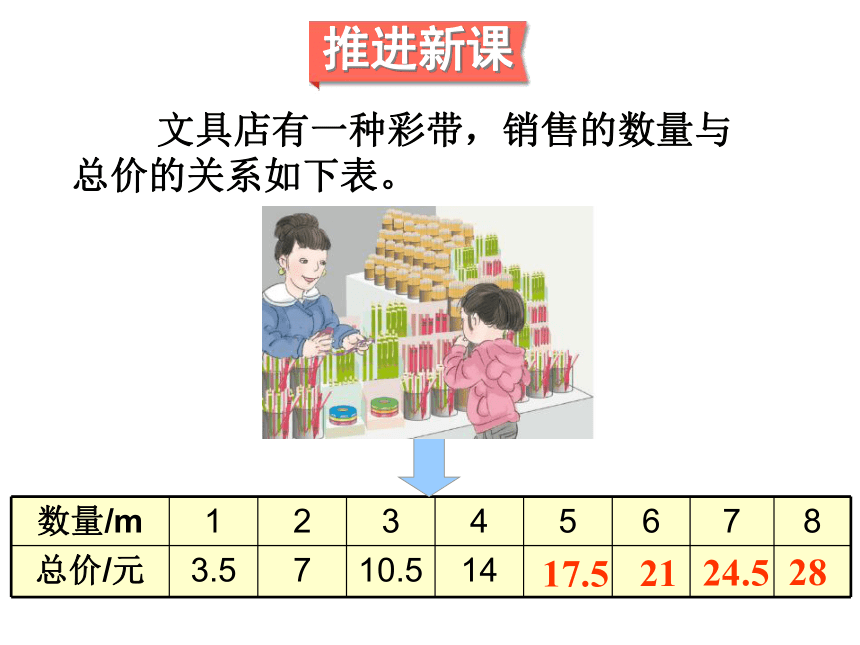
数量/m 1 2 3 4 5 6 7 8
总价/元 3.5 7 10.5 14
文具店有一种彩带,销售的数量与总价的关系如下表。
17.5
21
24.5
28
推进新课
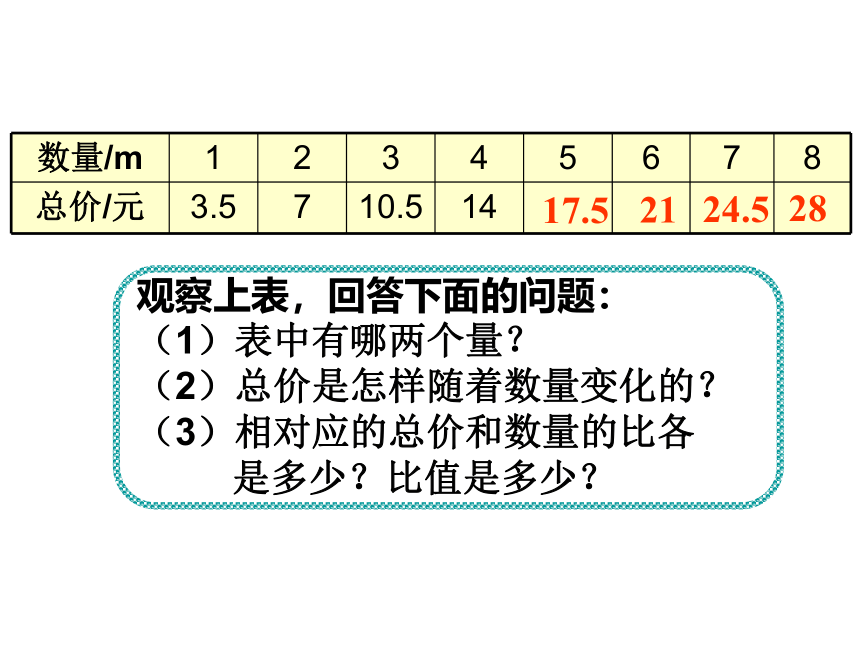
观察上表,回答下面的问题:
(1)表中有哪两个量?
(2)总价是怎样随着数量变化的?
(3)相对应的总价和数量的比各
是多少?比值是多少?
数量/m 1 2 3 4 5 6 7 8
总价/元 3.5 7 10.5 14
17.5
21
24.5
28
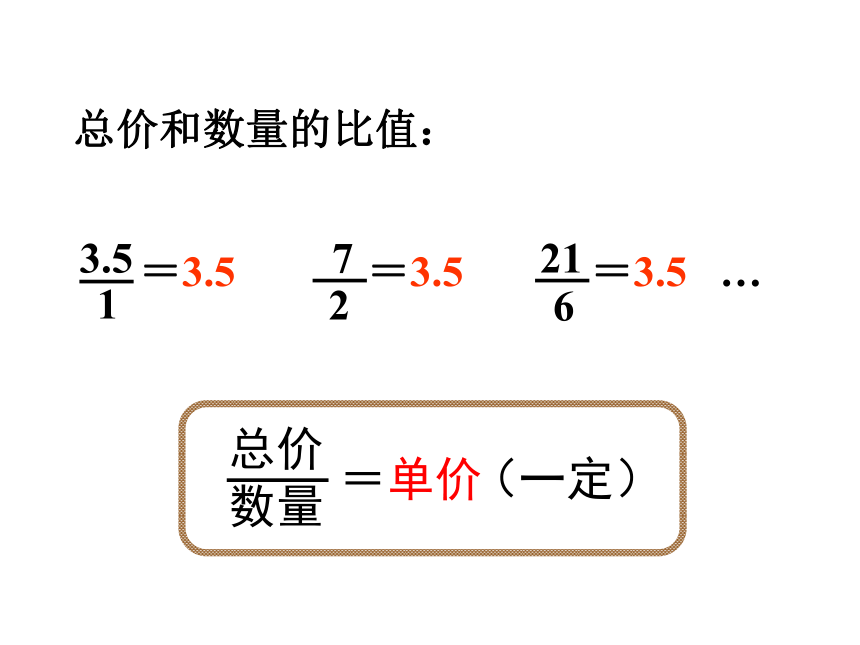
总价和数量的比值:
3.5
1
=3.5
7
2
=3.5
21
6
=3.5
…
总价
数量
=单价
(一定)
数量和总价是两种相关联的量,总价随着数量的变化而变化。
从表中可以发现数量增加了,总价也增加;数量减少,总价也减少。
总价和数量的比值总是一定的,这比值也就是单价,写成关系式就是
从题中可以得出:
总价
数量
=单价
(一定)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
上表中,总价和数量是成正比例的量,总价和数量成正比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),比例关系可以用这样的式子表示:
都有两种相关联的量。
都是一种量变化,另一种量也随着变化。
都是两种量中相对应的两个数的比值一定。像这样的两种量就叫做成正比例的量,
它们的关系叫做正比例关系。
根据上面对每个例子中各种量的分析,你发现它们有什么共同规律?
想一想,生活中还有哪些成正比例的量?
长方形的宽一定,面积和长成正比例;
每袋牛奶质量一定,牛奶袋数和总质量成正比例;
衣服的单价一定,购买衣服的数量和应付钱数成正比例;
地砖的面积一定,教室地板面积和地砖块数成正比例。
用字母表示正比例的关系
如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),比例关系可以用这样的式子表示:
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
我们一定要给自己提出这样的任务:第一,学习,第二是学习,第三还是学习。 —— 列宁
1.正比例
R·六年级下册
已知路程和时间,怎样求速度?
速度 = 路程÷时间
已知总价和数量,怎样求单价?
单价 = 总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作效率 = 工作总量÷工作时间
新课导入
下面是正方形的边长与周长的变化.
把表填完整.
边长/cm 周长/cm
1 4
0
2
4
6
8
10
12
1
2
3
4
边长/cm
周长/cm
14
16
2
8
3
12
4
16
观察数据,你有什么发现
数量/m 1 2 3 4 5 6 7 8
总价/元 3.5 7 10.5 14
文具店有一种彩带,销售的数量与总价的关系如下表。
17.5
21
24.5
28
推进新课
观察上表,回答下面的问题:
(1)表中有哪两个量?
(2)总价是怎样随着数量变化的?
(3)相对应的总价和数量的比各
是多少?比值是多少?
数量/m 1 2 3 4 5 6 7 8
总价/元 3.5 7 10.5 14
17.5
21
24.5
28
总价和数量的比值:
3.5
1
=3.5
7
2
=3.5
21
6
=3.5
…
总价
数量
=单价
(一定)
数量和总价是两种相关联的量,总价随着数量的变化而变化。
从表中可以发现数量增加了,总价也增加;数量减少,总价也减少。
总价和数量的比值总是一定的,这比值也就是单价,写成关系式就是
从题中可以得出:
总价
数量
=单价
(一定)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
上表中,总价和数量是成正比例的量,总价和数量成正比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),比例关系可以用这样的式子表示:
都有两种相关联的量。
都是一种量变化,另一种量也随着变化。
都是两种量中相对应的两个数的比值一定。像这样的两种量就叫做成正比例的量,
它们的关系叫做正比例关系。
根据上面对每个例子中各种量的分析,你发现它们有什么共同规律?
想一想,生活中还有哪些成正比例的量?
长方形的宽一定,面积和长成正比例;
每袋牛奶质量一定,牛奶袋数和总质量成正比例;
衣服的单价一定,购买衣服的数量和应付钱数成正比例;
地砖的面积一定,教室地板面积和地砖块数成正比例。
用字母表示正比例的关系
如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),比例关系可以用这样的式子表示:
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
我们一定要给自己提出这样的任务:第一,学习,第二是学习,第三还是学习。 —— 列宁
