五年级上册数学课件-3.3 三角形 北京版(共23张PPT)
文档属性
| 名称 | 五年级上册数学课件-3.3 三角形 北京版(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
三角形的面积
一、复习引入
高
底
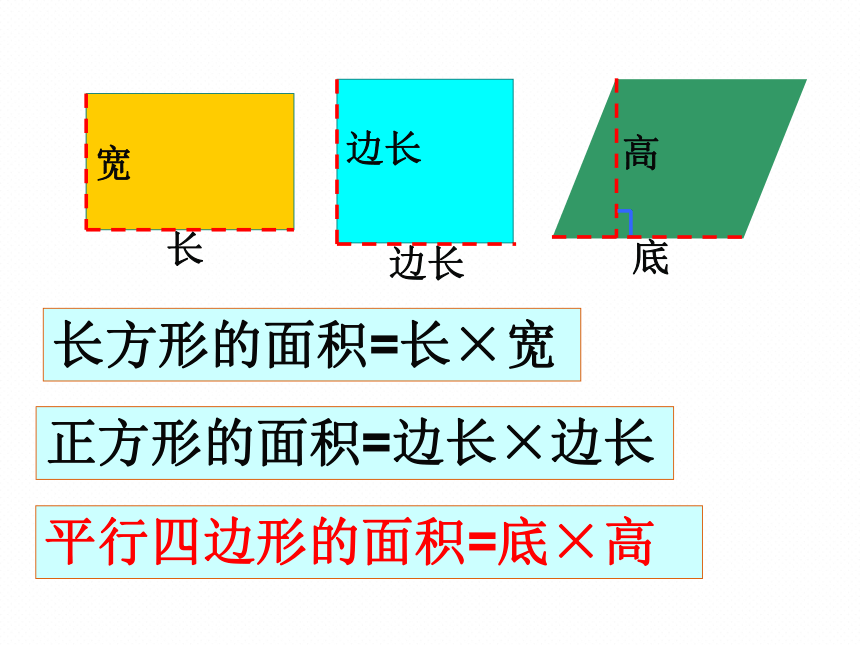
长方形的面积=长×宽
边长
边长
长
宽
正方形的面积=边长×边长
平行四边形的面积=底×高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
平行四边形
长方形
转化
剪、拼
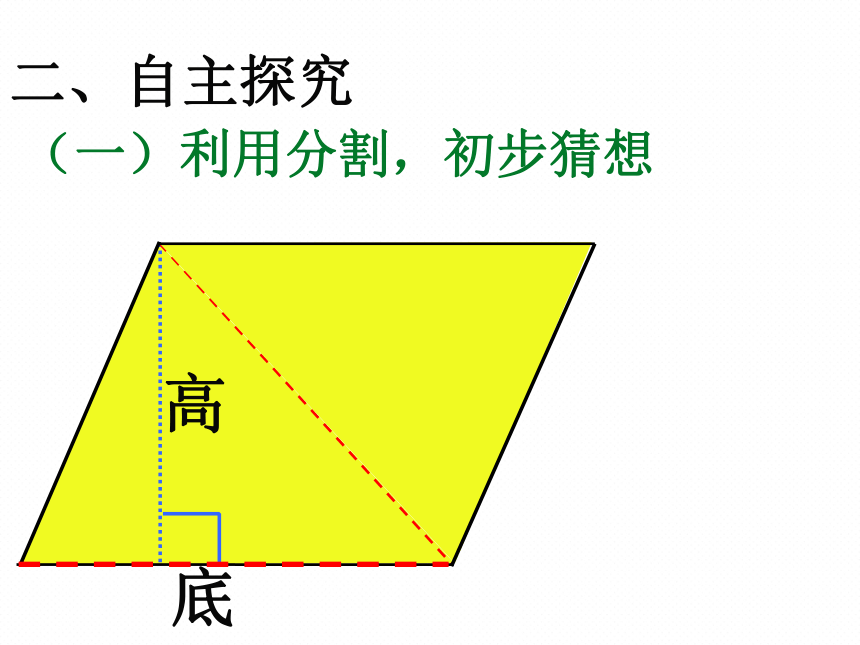
二、自主探究
(一)利用分割,初步猜想
底
高
1、平行四边形可以分成两个____________的三角形。
完全一样
2、分割后的三角形的底____原平行四边形的底。
=
3、分割后的三角形的高____原平行四边形的高。
=
三角形的面积=底×高÷2
底
高
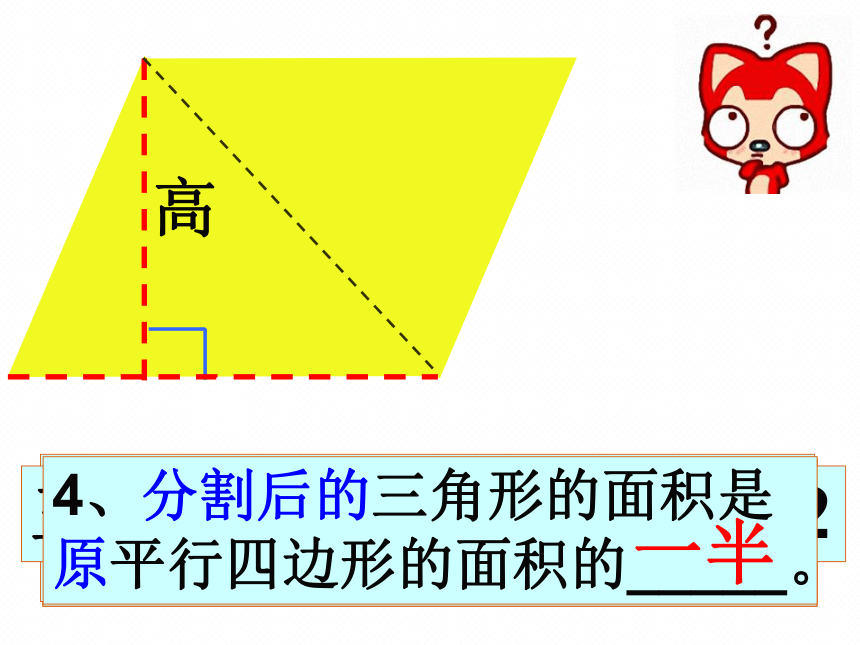
4、分割后的三角形的面积是原平行四边形的面积的_____。
一半
锐角三角形
钝角三角形
直角三角形
三、合作探究
活动要求:
(1)小组根据要求实验,分工合作。
(2)首先 ①选择合适的两个三角形;②在其中一个三角形中画一条高,并且标上相对应的底;③然后按住这个三角形固定不动;④旋转,移动另一个三角形,拼一拼,拼成平行四边形,并做好记录。
(3)实验完成后,小组讨论,检查,修改并完善记录。
四、展示提升
1. 原三角形的底与拼成后的平行四边形的底有什么关系?
2. 原三角形的高与拼成后的平行四边形的高有什么关系?
3. 其中一 个三角形的面积与拼成后的平行四边形的面积有什么关系?
1. 原三角形的底与拼成后的平行四边形的底相等。
2. 原三角形的高与拼成后的平行四边形的高有什么关系?
3. 其中一 个三角形的面积与拼成后的平行四边形的面积有什么关系?
1. 原三角形的底与拼成后的平行四边形的底相等。
3. 其中一 个三角形的面积与拼成后的平行四边形的面积有什么关系?
2. 原三角形的高与拼成后的平行四边形的高相等。
1. 原三角形的底与拼成后的平行四边形的底相等。
2. 原三角形的高与拼成后的平行四边形的高相等。
3. 其中一个三角形的面积是拼成后的平行四边形面积的一半。
红领巾的底是100cm,高是33cm,它的面积是多少平方厘米
S =ah÷2
=100×33÷2
=1650(c㎡)
答:它的面积是1650平方厘米。
100cm
33cm
五、练习巩固
1、(书本P92页第3题)如图,一种零件有一面是三角形。三角形的 ,
,这个三角形的面积是多少平方厘米?
答:这个三角形的面积是11.2cm 。
底是5.6cm
高是4cm
2、计算下面三角形的面积 。
4cm
3cm
6cm
30cm
S=ah 2
=3╳4 2
=6(cm2)
S=ah 2
=30╳ 6 2
=90(cm2)
20cm
(1)两个三角形可以拼成一个平行四边形。
两个完全一样的三角形可以拼成一个平行四边形。
(2)三角形的面积是平行四边形的面积的一半。
三角形的面积是与它等底等高的平行四边形面积的一半。
(3)三角形面积是S=ah
三角形面积是S=ah÷2
思考题:计算下列4个三角形的面积,你发现了什么规律?
6cm
10cm
①
②
③
④
等底等高的三角形面积相等。
三角形的面积
一、复习引入
高
底
长方形的面积=长×宽
边长
边长
长
宽
正方形的面积=边长×边长
平行四边形的面积=底×高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
平行四边形
长方形
转化
剪、拼
二、自主探究
(一)利用分割,初步猜想
底
高
1、平行四边形可以分成两个____________的三角形。
完全一样
2、分割后的三角形的底____原平行四边形的底。
=
3、分割后的三角形的高____原平行四边形的高。
=
三角形的面积=底×高÷2
底
高
4、分割后的三角形的面积是原平行四边形的面积的_____。
一半
锐角三角形
钝角三角形
直角三角形
三、合作探究
活动要求:
(1)小组根据要求实验,分工合作。
(2)首先 ①选择合适的两个三角形;②在其中一个三角形中画一条高,并且标上相对应的底;③然后按住这个三角形固定不动;④旋转,移动另一个三角形,拼一拼,拼成平行四边形,并做好记录。
(3)实验完成后,小组讨论,检查,修改并完善记录。
四、展示提升
1. 原三角形的底与拼成后的平行四边形的底有什么关系?
2. 原三角形的高与拼成后的平行四边形的高有什么关系?
3. 其中一 个三角形的面积与拼成后的平行四边形的面积有什么关系?
1. 原三角形的底与拼成后的平行四边形的底相等。
2. 原三角形的高与拼成后的平行四边形的高有什么关系?
3. 其中一 个三角形的面积与拼成后的平行四边形的面积有什么关系?
1. 原三角形的底与拼成后的平行四边形的底相等。
3. 其中一 个三角形的面积与拼成后的平行四边形的面积有什么关系?
2. 原三角形的高与拼成后的平行四边形的高相等。
1. 原三角形的底与拼成后的平行四边形的底相等。
2. 原三角形的高与拼成后的平行四边形的高相等。
3. 其中一个三角形的面积是拼成后的平行四边形面积的一半。
红领巾的底是100cm,高是33cm,它的面积是多少平方厘米
S =ah÷2
=100×33÷2
=1650(c㎡)
答:它的面积是1650平方厘米。
100cm
33cm
五、练习巩固
1、(书本P92页第3题)如图,一种零件有一面是三角形。三角形的 ,
,这个三角形的面积是多少平方厘米?
答:这个三角形的面积是11.2cm 。
底是5.6cm
高是4cm
2、计算下面三角形的面积 。
4cm
3cm
6cm
30cm
S=ah 2
=3╳4 2
=6(cm2)
S=ah 2
=30╳ 6 2
=90(cm2)
20cm
(1)两个三角形可以拼成一个平行四边形。
两个完全一样的三角形可以拼成一个平行四边形。
(2)三角形的面积是平行四边形的面积的一半。
三角形的面积是与它等底等高的平行四边形面积的一半。
(3)三角形面积是S=ah
三角形面积是S=ah÷2
思考题:计算下列4个三角形的面积,你发现了什么规律?
6cm
10cm
①
②
③
④
等底等高的三角形面积相等。
