数学人教A版2019选择性必修第一册第一章尖子生同步培优题典(1)word版含答案
文档属性
| 名称 | 数学人教A版2019选择性必修第一册第一章尖子生同步培优题典(1)word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-31 12:31:10 | ||
图片预览




文档简介
人教A版2019选择性必修第一册第一章
第I卷(选择题)
请点击修改第I卷的文字说明
一、单选题
1.在正三棱柱中,,点满足,其中,则( )
A.当时,△的周长为定值
B.当时,三棱锥的体积不是定值
C.当时,有且仅有一个点,使得
D.当时,有且仅有一个点,使得平面
2.如图所示的木质正四棱锥模型,过点A作一个平面分别交于点E,F,G,若,则的值为( )
A. B. C. D.
3.已知空间向量两两的夹角均为,且,.若向量满足,,则的最大值是( )
A. B. C. D.
4.已知长方体中,,,,空间中存在一动点满足,记,,,则( ).
A.存在点,使得 B.存在点,使得
C.对任意的点,有 D.对任意的点,有
5.如图,矩形ABCD中,,E为边AB的中点,将沿直线DE翻折成.在翻折过程中,直线与平面ABCD所成角的正弦值最大为( )
A. B. C. D.
6.如图,在矩形ABCD中,AB=2,BC=1,E、N分别为边AB,BC的中点,沿DE将△ADE折起,点A折至A1处(A1与A不重合),若M、K分别为线段A1D,A1C的中点,则在MDE折起过程中,( )
A.DE可以与A1C垂直
B.不能同时做到MN//平面A1BE且BK//平面A1DE
C.当MN⊥A1D时,MN⊥平面A1DE
D.直线A1C、BK与平面BCDE所成角分别为θ1、θ2,θ1,θ2能够同时取得最大值
二、多选题
7.已知正方体的棱长为,点是棱的中点,点在面内(包含边界),且,则( )
A.点的轨迹的长度为
B.存在,使得
C.直线与平面所成角的正弦值最大为
D.沿线段的轨迹将正方体切割成两部分,挖去体积较小部分,剩余部分几何体的表面积为
8.如图四棱锥,平面平面,侧面是边长为的正三角形,底面为矩形,,点是的中点,则下列结论正确的是( )
A.平面
B.与平面所成角的余弦值为
C.三棱锥的体积为
D.四棱锥外接球的内接正四面体的表面积为
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
9.空间向量,,,,,,且,,若点P满足,且,,,,则动点P的轨迹所形成的空间区域的体积为__________.
10.在正四棱锥中,底面边长为,侧棱,为的中点,为直线上一点,且与、不重合,若异面直线与所成角为,则三棱锥的体积为______.
11.在四面体中,若,,,底面是边长为的正三角形,为的中心,则的余弦值为______.
12.在三棱锥中,,是正三角形,为中点,有以下四个结论:
①若,则三棱锥的体积为;
②若,且三棱锥的四个顶点都在球O的球面上,则球O的体积为;
③若,则三棱锥的体积为;
④若,且三棱锥的四个顶点都在球O的球面上,则球O的表面积为.
其中结论正确的序号为____________.
四、解答题
13.如图,在中,,,为的外心,平面,且.
(1)求证:平面;并计算与平面之间的距离.
(2)设平面平面,若点在线段上运动,当直线与平面所成角取最大值时,求二面角的正弦值.
14.如图1,直角梯形ABCD中,AB∥CD,AB⊥AD,AB=2AD=2DC=6.如图2,将图1中△DAC沿AC折起,使得点D在平面ABC上的正投影G在△ABC内部,点E为AB的中点,连接DB,DE,三棱锥D ABC的体积为12.对于图2的几何体.
(1)求证:DE⊥AC;
(2)求DB与平面DAC所成角的余弦值.
15.如图,在四棱锥中,底面为边长为2的菱形,为正三角形,且平面平面,为线段中点,在线段上.
(1)当是线段中点时,求证:平面;
(2)当时,求二面角的正弦值.
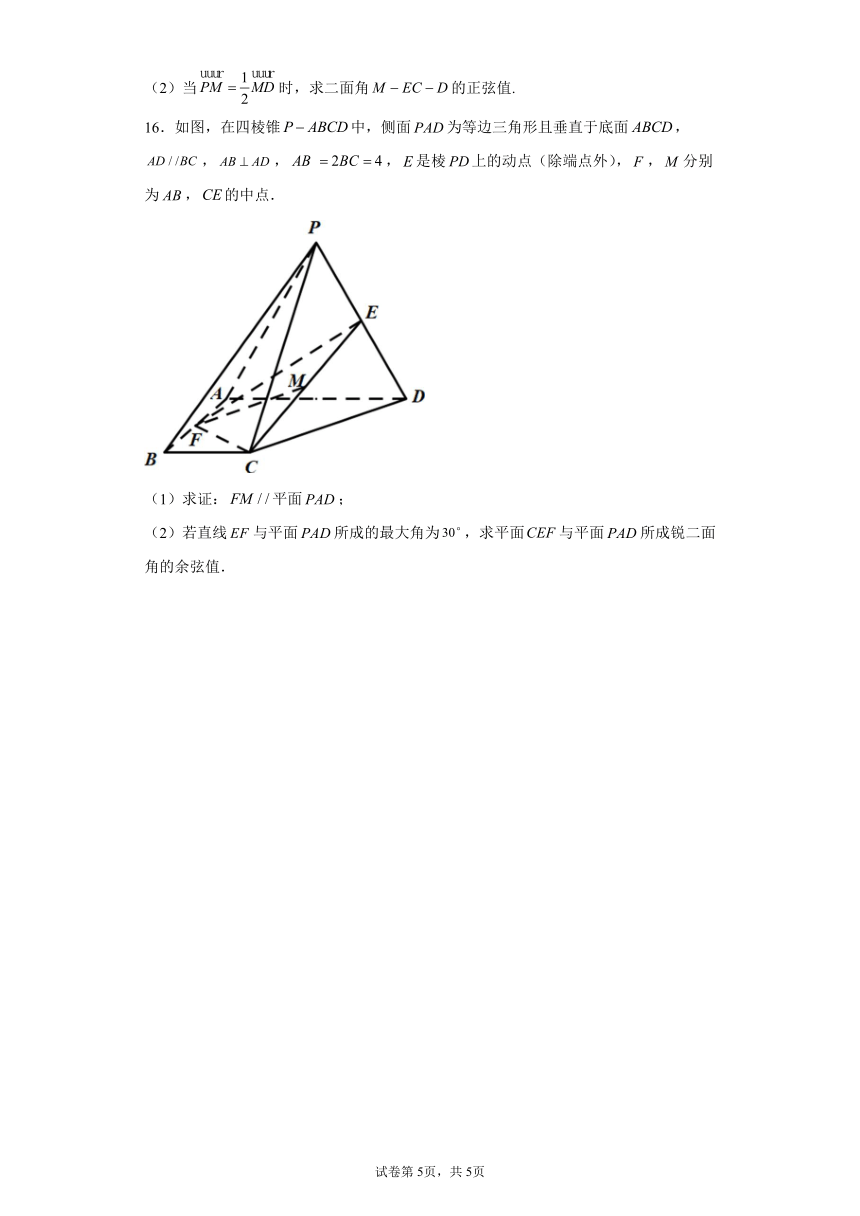
16.如图,在四棱锥中,侧面为等边三角形且垂直于底面,,,,是棱上的动点(除端点外),,分别为,的中点.
(1)求证:平面;
(2)若直线与平面所成的最大角为,求平面与平面所成锐二面角的余弦值.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
【分析】
判断当时在线段上,分别计算点为两个特殊点时的周长,即可判断A;当时在线段上,利用线面平行的性质以及锥体的体积公式,即可判断B;当时,取线段,的中点分别为,,连结,则在线段上,分别取在,处,得到均满足,即可判断C;当时,取的中,的中点,则在线的上,证明当在点处时,平面,利用过定与定直线垂直的平面有且只有一个,即可判断D.
【详解】
A:当时,,即,所以,
故在线段上,此时△的周长为,
当为的中点时,△的周长为,
当在点处时,△的周长为,
故周长不为定值,故错误;
B:当时,,即,所以,
故在线段上,又,面,面,则面,
∴直线上的点到平面的距离相等,又△的面积为定值,
∴三棱锥的体积为定值,故错误;
C:当时,取线段,的中点分别为,,连结,
由,即,所以,则在线段上,
当在处时,,,又,则平面,
又平面,所以,即,
同理,当在处,,故错误;
D:当时,取的中点,的中点,
由,即,所以,则在线的上,
当在点处时,取的中点,连结,,
由正三棱柱的性质知:面,又面,所以,
在正方形中,,又,、面,
故面,又面,所以,
在正方体形中,又,、面,
∴平面,过定点与定直线垂直的平面有且只有一个,
故有且仅有一个点,使得平面,故正确.
故选:D.
【点睛】
关键点点睛:根据各选项给定的参数值,结合题设向量的线性关系判断的位置,再由三棱锥的体积公式、线面垂直的判定及性质判断各项的正误.
2.C
【分析】
以AC、BD交点O为坐标原点,射线OA、OB、OP为x、y、z轴正方向建立空间直角坐标系,设,,,, (a、b>0),进而写出、、、坐标,可得,,由四点共面有,设,求值即可得答案.
【详解】
解:建立如图所示空间直角坐标系,设,,,, (a、b>0),则,,,,
∴,,
由题意四点共面,则有,其中,
设,
∴
由方程组,即,解得,
所以,
故选:C.
3.C
【分析】
根据题意,取一个三棱锥,用其棱表示对应的向量,结合题中所给的条件,将相应的边长求出,之后应用空间向量运算法则,表示出对应的结果,从而判断出取最值时对应的情况,求值即可.
【详解】
取一三棱锥,,
且,,所以,
,
令,
因为,,
根据数量积的运算率可知:,,
又,,
所以,
所以,
得,
分别取中点,
所以,,,
所以,
所以当四点共线且按此顺序排列时,的最大值为:,
故选:C.
【点睛】
该题考查的是有关空间向量的运算问题,涉及到的知识点有空间向量运算法则,三角形中利用余弦定理求边长,属于较难题目.
4.C
【分析】
建立空间直角坐标系,由题意可得各顶点的坐标,由,设的坐标为,可得、、的取值范围都为,求出数量积,由的坐标的范围可得答案.
【详解】
以为轴,为轴,为轴,为坐标原点,建立如图所示的空间直角坐标系,
则,、,,设点,
所以,,,,,
因为,所以,,,,,
,,
,
恒成立,故C正确,A不正确;
,令,则,
,矛盾,所以B不正确;
恒成立,所以D不正确.
故选:C.
【点睛】
本题考查了空间向量数量积的大小比较,考查了推理能力与计算能力,属于难题.
5.A
【分析】
分别取DE,DC的中点O,F,点A的轨迹是以AF为直径的圆,以为轴,过与平面垂直的直线为轴建立坐标系,利用向量法求出正弦值为,换元后利用基本不等式可得答案.
【详解】
分别取DE,DC的中点O,F,则点A的轨迹是以AF为直径的圆,
以为轴,过与平面垂直的直线为轴建立坐标系,
则,平面ABCD的其中一个法向量为= (0,0.1),
由,设,则,
记直线与平面ABCD所成角为,
则
设,
所以直线与平面ABCD所成角的正弦值最大为,
故选:A.
【点睛】
本题主要考查利用向量法求线面角,考查了三角函数的恒的变换以及基本不等式的应用,考查了空间想象能力与计算能力,属于综合题.
6.D
【分析】
假设DE⊥A1C,由线面垂直的判定及性质可判断A;取DE,DC中点G,F,连接GM,GN,FK,FB,根据面面平行的判定及性质可判断B;连接ME,EN,DN,通过说明MN与ME不垂直即可判断C;找到点A1的轨迹,证明的长度为定值,结合线面角的概念可判断D;即可得解.
【详解】
对于A,连接EC,如图,
假设DE⊥A1C,由平面几何的知识可得DE⊥EC,
∴DE⊥平面A1EC,∴DE⊥A1E,而A1ED=45°,故假设不成立,∴A错误;
对于B,取DE,DC中点G,F,连接GM,GN,FK,FB,如图,
∴GM//A1E,GN//EB,FK//A1D,BF//DE,
∴平面A1BE//平面GMN,平面FKB//平面A1DE,
故能同时做到MN//平面A1BE且BK//平面A1DE,∴B错误;
对于C,连接ME,EN,DN,如图,
当MN⊥A1D时,,
而,∴MN与ME不垂直,即MN不垂直平面A1DE,∴C错误;
对于D,∵A1在以DE为直径球面上,球心为G,且A1G⊥DE,
∴A1的轨迹为圆弧(A1与A不重合,在平面下方时与该情况一致),如图弧AF所示,
∴当点A1到平面BCDE的距离最大时,直线A1C与平面BCDE所成角取得最大值;
连接EC,取EC中点T,连接TK,TB,如图,
∴,,
又,,∴,
∴,为定值,
∴当点K到平面BCDE的距离最大时,直线BK与平面BCDE所成角取得最大值,
此时点A1到平面BCDE的距离也最大,∴D正确.
故选:D.
【点睛】
本题考查了线线、线面位置关系的判定与性质及线面角相关内容的求解,考查了空间思维能力,综合性较强,属于难题.
7.ACD
【分析】
计算出的长,可判断A选项的正误;以为原点,、、所在直线分别为、、轴建立空间直角坐标系,利用空间向量法可判断BC选项的正误;计算出挖去部分的面积和新增部分的面积,可判断出D选项的正误.
【详解】
如图1,取中点,连接,
因为且,且、分别为、的中点,故且,
所以,四边形为平行四边形,可得且,
因为底面,故底面,底面,,
因为,,
所以点的轨迹是以为圆心,半径以的圆位于正方形内的部分,
故点的轨迹长度为,A正确;
以为原点,、、所在直线分别为、、轴建立空间直角坐标系,如图2,
则、、,、、,
设.
,,
,B错误;
设平面的法向量为,,,
由,取,可得,
,
,则,所以,当时,即当时,
取得最大值,故C正确;
如图1,挖去部分为半圆锥,原正方体的表面积为,
挖去部分面积为,新增部分面积为,
所以新几何体的表面积为,故D正确.
故选:ACD.
【点睛】
方法点睛:求空间角的常用方法:
(1)定义法:由异面直线所成角、线面角、二面角的定义,结合图形,作出所求空间角,再结合题中条件,解对应的三角形,即可求出结果;
(2)向量法:建立适当的空间直角坐标系,通过计算向量的夹角(两直线的方向向量、直线的方向向量与平面的法向量、两平面的法向量)的余弦值,即可求得结果.
8.BD
【分析】
取的中点,的中点,连接,则由已知可得平面 ,而底面为矩形,所以以为坐标原点,分别以所在的直线为轴,轴 ,轴,建立空间直角坐标系,利用空间向量依次求解即可.
【详解】
解:取的中点,的中点,连接,
因为三角形为等边三角形,所以,
因为平面平面,所以平面 ,
因为,所以两两垂直,
所以,如下图,以为坐标原点,分别以所在的直线为轴,轴 ,轴,
建立空间直角坐标系,则,
,
因为点是的中点,所以,
平面的一个法向量为,
,显然 与不共线,
所以与平面不垂直,所以A不正确;
,
设平面的法向量为,则
,
令,则,
所以,
设与平面所成角为,
则,
所以,所以B正确;
三棱锥的体积为
,
所以C不正确;
设四棱锥外接球的球心为,则,
所以,
解得,即为矩形对角线的交点,
所以四棱锥外接球的半径为3,
设四棱锥外接球的内接正四面体的棱长为,
将四面体拓展成正方体,其中正四面体棱为正方体面的对角线,
故正方体的棱长为,所以,得,
所以正四面体的表面积为,所以D正确.
故选:BD
【点睛】
此题考查线面垂直,线面角,棱锥的体积,棱锥的外接球等知识,综合性强,考查了计算能力,属于较难题.
9.
【分析】
先分析若,,,时,点在图中的点,
由,,,可得,,,可以得出点在三棱锥内,计算三棱锥的体积即可求解.
【详解】
因为,,,,
当,,时,点在图中的点,
因为,当,时,
同理,,
,,,
由知点在内,
而,,,,
所以点在三棱锥内,
且,,,
过作平面的垂线,垂足为,
由三余弦定理可得:,即,
所以,所以,
,
所以三棱锥的体积为,
故答案为:.
【点睛】
关键点点睛:本题解题的关键是由可得是以为邻边所成的平行六面体的体对角线,关键点是分析出,,,得出点在三棱锥内.
10.
【分析】
本题首先可以绘出正四棱锥的图像并构建空间直角坐标系,然后设,根据异面直线与所成角为计算出,再然后设点到底面的距离为以及点到底面的距离为并根据三角形相似的性质得出,最后根据三棱锥的体积公式即可得出结果.
【详解】
如图,设点为底面正方形的中心,取的中点,
以为坐标原点,分别以直线、、为、、轴建立空间直角坐标系,
易知,,,,
,,,
设(且),
则,
由,
整理得,解得(舍去),
故,且点在射线上,
设点到底面的距离为,点到底面的距离为,
因为,,
所以,,
故答案为:.
【点睛】
本题考查几何体体积的求法,考查异面直线所成角的灵活应用,考查三棱锥的体积公式,考查运算能力和空间想象能力,体现了综合性,是难题.
11.
【分析】
如图建立空间坐标系,利用长度关系明确P点坐标,借助向量夹角公式得到结果.
【详解】
,
设
∵
∴
,
故答案为:
【点睛】
本题以棱锥为背景,考查角的大小的度量,考查空间坐标法,考查空间想象能力与计算能力,属于中档题.
12.①②④
【分析】
取中点,建立合适的空间直角坐标系,利用平面几何知识求出所需点的坐标,然后将垂直关系转化我向量的数量积为,求出的长度,再利用球的体积公式和表面积公式进行判断即可得到答案.
【详解】
取中点,连接,以为坐标原点,为轴,为轴建立空间直角坐标系如图所示,
设,则,,,,,
所以,
由,是正三角形,得三棱锥为正三棱锥,
设外接球球心为,半径为,则,且轴,
所以,,
解得,
若,则,,
所以,解得:,
所以,故选项①正确;
又,所以,故选项②正确;
若,则,
所以,解得:,故选项③错误;
又,所以,故选项④正确;
故答案为:①②④.
13.(1)证明见解析,(2)
【分析】
(1)先证明四边形为菱形,即可说明,则可得出平面,由到平面的距离即为点到平面的距离,借助则可计算出结果.
(2)建立空间直角坐标系,由题意可说明,设,求出平面的法向量为,根据与所成角的余弦值可表示出直线直线与平面所成角的正弦值,即可求出其取最大值时的,则可求出点的坐标,再求出平面的法向量为,由二面角的余弦公式则可求出二面角的正弦值.
【详解】
(1)如图,连接,交于点,为的外心,
所以,
所以.
故和都为等边三角形,
即四边形为菱形,
所以且.
又平面、平面 ,
所以平面.
则到平面的距离即为点到平面的距离,记为 ,
由题意知:,
所以, .
又因为
即
解得:.
(2)因为平面,平面,平面平面=,
所以.
如图所示:以点为原点建系.则.
设,
所以.
设平面的法向量为.
则
所以直线与平面所成角的正弦值为:,
即当时直线与平面所成角取最大值.
此时,
所以,
设平面的法向量为.
则令则.
所以,即
则二面角的正弦值.
14.(1)证明见解析;(2).
【分析】
(1)根据条件,先利用线面垂直的判定定理证明AC⊥平面DEF,进而证得DE⊥AC;
(2)先用等积法算出DG,进而算出GF,然后建立空间直角坐标系,通过空间向量线面角的求法求得答案.
【详解】
(1)取AC的中点F,连接DF,CE,EF,
则△DAC,△EAC均为等腰直角三角形.
∴AC⊥DF,AC⊥EF,∵DF∩EF=F,∴AC⊥平面DEF,又DE 平面DEF,∴DE⊥AC.
(2)连接GA,GC.
∵DG⊥平面ABC,而GA 平面ABC,GC 平面ABC,∴DG⊥GA,DG⊥GC,
又DA=DC,∴GA=GC,∴G在AC的垂直平分线上,又EA=EC,∴E在AC的垂直平分线上,∴EG垂直平分AC,又F为AC的中点,∴E,F,G共线.
由AB=2AD=2DC=6,知△ABC为等腰直角三角形,
∴S△ABC=×AC×BC=×6×6=18,∴VDABC=×S△ABC×DG=×18×DG=12,
∴DG=2.
在等腰直角三角形DAC和等腰直角三角形EAC中,EF=DF=AC=3,
在Rt△DGF中,GF=.
过G作平行于AC的直线MN,以G为坐标原点,GM为x轴,GE为y轴,GD为z轴,建立如图所示的空间直角坐标系,
则A(3,-1,0),B(-3,5,0),C(-3,-1,0),D(0,0,2).
∴=(-3,5,-2).
设平面DAC的法向量为=(x,y,z),
又=(3,-1,-2),=(-3,-1,-2),
由,得:,令z=1,得:,
于是,,
故DB与平面DAC所成角的余弦值为.
15.(1)证明见解析;(2)
【分析】
(1)连结,交于点,连结,由中位线性质可得,利用线面平行的判定定理可得平面;
(2)易得,由线面垂直的性质定理可得面,,以为原点,以为轴,建立空间直角坐标系,利用空间向量求二面角的余弦值即可解.
【详解】
证明:(1)连结,交于点,连结,
由底面为菱形,为中点,
∵为中点,∴.
又面,面,∴面.
(2)∵为正三角形,为的中点,∴.
又∵面面,∴面,
又底面菱形,,为线段中点,
以为原点,以为轴,建立空间直角坐标系,则,,
,,,则
又,即,可得,
,
设平面的法向量为,则
,令,则
由面,所以平面的法向量为,
所以
所以二面角的正弦值为
【点睛】
方法点睛:本题考查线面平行的判定定理及面面垂直的性质定理,及面面角的求法,利用空间向量求立体几何常考查的夹角:
设直线的方向向量分别为,平面的法向量分别为,则
①两直线所成的角为(),;
②直线与平面所成的角为(),;
③二面角的大小为(),
16.(1)证明见解析;(2).
【分析】
(1)取的中点,连结,,证明平面平面,再用面面平行的性质定理证明即可;
(2)作出直线与平面所成角的平面角,通过最大角为,确定长度,建立空间直角坐标系,用向量法计算二面角余弦值.
【详解】
(1)证明:取的中点,连结,,
因为,分别为,的中点,
所以,
又因为平面,平面,
所以平面,
同理,平面,
又因为,
所以平面平面,
又因为平面,
所以平面.
(2)因为平面平面,,
所以平面,
所以即为直线与平面所成的角,
且,
当最小,即为中点时,,
此时最大为,
又因为,
所以,所以.
取的中点,连结,,
易知平面,
因为且,
所以四边形为平行四边形,
所以,
以为坐标原点,的方向为轴正方向,建立如图所示的空间直角坐标系.
则,,,,,,,,
设为平面的法向量,
则,
即
可取.
设平面的法向量为,
所以,
所以平面与平面所成锐二面角的余弦值为.
【点睛】
求直线与平面所成的角的一般步骤:
①找直线与平面所成的角,即通过找直线在平面上的射影来完成;
②计算,要把直线与平面所成的角转化到一个三角形中求解.
答案第1页,共2页
答案第1页,共2页
第I卷(选择题)
请点击修改第I卷的文字说明
一、单选题
1.在正三棱柱中,,点满足,其中,则( )
A.当时,△的周长为定值
B.当时,三棱锥的体积不是定值
C.当时,有且仅有一个点,使得
D.当时,有且仅有一个点,使得平面
2.如图所示的木质正四棱锥模型,过点A作一个平面分别交于点E,F,G,若,则的值为( )
A. B. C. D.
3.已知空间向量两两的夹角均为,且,.若向量满足,,则的最大值是( )
A. B. C. D.
4.已知长方体中,,,,空间中存在一动点满足,记,,,则( ).
A.存在点,使得 B.存在点,使得
C.对任意的点,有 D.对任意的点,有
5.如图,矩形ABCD中,,E为边AB的中点,将沿直线DE翻折成.在翻折过程中,直线与平面ABCD所成角的正弦值最大为( )
A. B. C. D.
6.如图,在矩形ABCD中,AB=2,BC=1,E、N分别为边AB,BC的中点,沿DE将△ADE折起,点A折至A1处(A1与A不重合),若M、K分别为线段A1D,A1C的中点,则在MDE折起过程中,( )
A.DE可以与A1C垂直
B.不能同时做到MN//平面A1BE且BK//平面A1DE
C.当MN⊥A1D时,MN⊥平面A1DE
D.直线A1C、BK与平面BCDE所成角分别为θ1、θ2,θ1,θ2能够同时取得最大值
二、多选题
7.已知正方体的棱长为,点是棱的中点,点在面内(包含边界),且,则( )
A.点的轨迹的长度为
B.存在,使得
C.直线与平面所成角的正弦值最大为
D.沿线段的轨迹将正方体切割成两部分,挖去体积较小部分,剩余部分几何体的表面积为
8.如图四棱锥,平面平面,侧面是边长为的正三角形,底面为矩形,,点是的中点,则下列结论正确的是( )
A.平面
B.与平面所成角的余弦值为
C.三棱锥的体积为
D.四棱锥外接球的内接正四面体的表面积为
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
9.空间向量,,,,,,且,,若点P满足,且,,,,则动点P的轨迹所形成的空间区域的体积为__________.
10.在正四棱锥中,底面边长为,侧棱,为的中点,为直线上一点,且与、不重合,若异面直线与所成角为,则三棱锥的体积为______.
11.在四面体中,若,,,底面是边长为的正三角形,为的中心,则的余弦值为______.
12.在三棱锥中,,是正三角形,为中点,有以下四个结论:
①若,则三棱锥的体积为;
②若,且三棱锥的四个顶点都在球O的球面上,则球O的体积为;
③若,则三棱锥的体积为;
④若,且三棱锥的四个顶点都在球O的球面上,则球O的表面积为.
其中结论正确的序号为____________.
四、解答题
13.如图,在中,,,为的外心,平面,且.
(1)求证:平面;并计算与平面之间的距离.
(2)设平面平面,若点在线段上运动,当直线与平面所成角取最大值时,求二面角的正弦值.
14.如图1,直角梯形ABCD中,AB∥CD,AB⊥AD,AB=2AD=2DC=6.如图2,将图1中△DAC沿AC折起,使得点D在平面ABC上的正投影G在△ABC内部,点E为AB的中点,连接DB,DE,三棱锥D ABC的体积为12.对于图2的几何体.
(1)求证:DE⊥AC;
(2)求DB与平面DAC所成角的余弦值.
15.如图,在四棱锥中,底面为边长为2的菱形,为正三角形,且平面平面,为线段中点,在线段上.
(1)当是线段中点时,求证:平面;
(2)当时,求二面角的正弦值.
16.如图,在四棱锥中,侧面为等边三角形且垂直于底面,,,,是棱上的动点(除端点外),,分别为,的中点.
(1)求证:平面;
(2)若直线与平面所成的最大角为,求平面与平面所成锐二面角的余弦值.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
【分析】
判断当时在线段上,分别计算点为两个特殊点时的周长,即可判断A;当时在线段上,利用线面平行的性质以及锥体的体积公式,即可判断B;当时,取线段,的中点分别为,,连结,则在线段上,分别取在,处,得到均满足,即可判断C;当时,取的中,的中点,则在线的上,证明当在点处时,平面,利用过定与定直线垂直的平面有且只有一个,即可判断D.
【详解】
A:当时,,即,所以,
故在线段上,此时△的周长为,
当为的中点时,△的周长为,
当在点处时,△的周长为,
故周长不为定值,故错误;
B:当时,,即,所以,
故在线段上,又,面,面,则面,
∴直线上的点到平面的距离相等,又△的面积为定值,
∴三棱锥的体积为定值,故错误;
C:当时,取线段,的中点分别为,,连结,
由,即,所以,则在线段上,
当在处时,,,又,则平面,
又平面,所以,即,
同理,当在处,,故错误;
D:当时,取的中点,的中点,
由,即,所以,则在线的上,
当在点处时,取的中点,连结,,
由正三棱柱的性质知:面,又面,所以,
在正方形中,,又,、面,
故面,又面,所以,
在正方体形中,又,、面,
∴平面,过定点与定直线垂直的平面有且只有一个,
故有且仅有一个点,使得平面,故正确.
故选:D.
【点睛】
关键点点睛:根据各选项给定的参数值,结合题设向量的线性关系判断的位置,再由三棱锥的体积公式、线面垂直的判定及性质判断各项的正误.
2.C
【分析】
以AC、BD交点O为坐标原点,射线OA、OB、OP为x、y、z轴正方向建立空间直角坐标系,设,,,, (a、b>0),进而写出、、、坐标,可得,,由四点共面有,设,求值即可得答案.
【详解】
解:建立如图所示空间直角坐标系,设,,,, (a、b>0),则,,,,
∴,,
由题意四点共面,则有,其中,
设,
∴
由方程组,即,解得,
所以,
故选:C.
3.C
【分析】
根据题意,取一个三棱锥,用其棱表示对应的向量,结合题中所给的条件,将相应的边长求出,之后应用空间向量运算法则,表示出对应的结果,从而判断出取最值时对应的情况,求值即可.
【详解】
取一三棱锥,,
且,,所以,
,
令,
因为,,
根据数量积的运算率可知:,,
又,,
所以,
所以,
得,
分别取中点,
所以,,,
所以,
所以当四点共线且按此顺序排列时,的最大值为:,
故选:C.
【点睛】
该题考查的是有关空间向量的运算问题,涉及到的知识点有空间向量运算法则,三角形中利用余弦定理求边长,属于较难题目.
4.C
【分析】
建立空间直角坐标系,由题意可得各顶点的坐标,由,设的坐标为,可得、、的取值范围都为,求出数量积,由的坐标的范围可得答案.
【详解】
以为轴,为轴,为轴,为坐标原点,建立如图所示的空间直角坐标系,
则,、,,设点,
所以,,,,,
因为,所以,,,,,
,,
,
恒成立,故C正确,A不正确;
,令,则,
,矛盾,所以B不正确;
恒成立,所以D不正确.
故选:C.
【点睛】
本题考查了空间向量数量积的大小比较,考查了推理能力与计算能力,属于难题.
5.A
【分析】
分别取DE,DC的中点O,F,点A的轨迹是以AF为直径的圆,以为轴,过与平面垂直的直线为轴建立坐标系,利用向量法求出正弦值为,换元后利用基本不等式可得答案.
【详解】
分别取DE,DC的中点O,F,则点A的轨迹是以AF为直径的圆,
以为轴,过与平面垂直的直线为轴建立坐标系,
则,平面ABCD的其中一个法向量为= (0,0.1),
由,设,则,
记直线与平面ABCD所成角为,
则
设,
所以直线与平面ABCD所成角的正弦值最大为,
故选:A.
【点睛】
本题主要考查利用向量法求线面角,考查了三角函数的恒的变换以及基本不等式的应用,考查了空间想象能力与计算能力,属于综合题.
6.D
【分析】
假设DE⊥A1C,由线面垂直的判定及性质可判断A;取DE,DC中点G,F,连接GM,GN,FK,FB,根据面面平行的判定及性质可判断B;连接ME,EN,DN,通过说明MN与ME不垂直即可判断C;找到点A1的轨迹,证明的长度为定值,结合线面角的概念可判断D;即可得解.
【详解】
对于A,连接EC,如图,
假设DE⊥A1C,由平面几何的知识可得DE⊥EC,
∴DE⊥平面A1EC,∴DE⊥A1E,而A1ED=45°,故假设不成立,∴A错误;
对于B,取DE,DC中点G,F,连接GM,GN,FK,FB,如图,
∴GM//A1E,GN//EB,FK//A1D,BF//DE,
∴平面A1BE//平面GMN,平面FKB//平面A1DE,
故能同时做到MN//平面A1BE且BK//平面A1DE,∴B错误;
对于C,连接ME,EN,DN,如图,
当MN⊥A1D时,,
而,∴MN与ME不垂直,即MN不垂直平面A1DE,∴C错误;
对于D,∵A1在以DE为直径球面上,球心为G,且A1G⊥DE,
∴A1的轨迹为圆弧(A1与A不重合,在平面下方时与该情况一致),如图弧AF所示,
∴当点A1到平面BCDE的距离最大时,直线A1C与平面BCDE所成角取得最大值;
连接EC,取EC中点T,连接TK,TB,如图,
∴,,
又,,∴,
∴,为定值,
∴当点K到平面BCDE的距离最大时,直线BK与平面BCDE所成角取得最大值,
此时点A1到平面BCDE的距离也最大,∴D正确.
故选:D.
【点睛】
本题考查了线线、线面位置关系的判定与性质及线面角相关内容的求解,考查了空间思维能力,综合性较强,属于难题.
7.ACD
【分析】
计算出的长,可判断A选项的正误;以为原点,、、所在直线分别为、、轴建立空间直角坐标系,利用空间向量法可判断BC选项的正误;计算出挖去部分的面积和新增部分的面积,可判断出D选项的正误.
【详解】
如图1,取中点,连接,
因为且,且、分别为、的中点,故且,
所以,四边形为平行四边形,可得且,
因为底面,故底面,底面,,
因为,,
所以点的轨迹是以为圆心,半径以的圆位于正方形内的部分,
故点的轨迹长度为,A正确;
以为原点,、、所在直线分别为、、轴建立空间直角坐标系,如图2,
则、、,、、,
设.
,,
,B错误;
设平面的法向量为,,,
由,取,可得,
,
,则,所以,当时,即当时,
取得最大值,故C正确;
如图1,挖去部分为半圆锥,原正方体的表面积为,
挖去部分面积为,新增部分面积为,
所以新几何体的表面积为,故D正确.
故选:ACD.
【点睛】
方法点睛:求空间角的常用方法:
(1)定义法:由异面直线所成角、线面角、二面角的定义,结合图形,作出所求空间角,再结合题中条件,解对应的三角形,即可求出结果;
(2)向量法:建立适当的空间直角坐标系,通过计算向量的夹角(两直线的方向向量、直线的方向向量与平面的法向量、两平面的法向量)的余弦值,即可求得结果.
8.BD
【分析】
取的中点,的中点,连接,则由已知可得平面 ,而底面为矩形,所以以为坐标原点,分别以所在的直线为轴,轴 ,轴,建立空间直角坐标系,利用空间向量依次求解即可.
【详解】
解:取的中点,的中点,连接,
因为三角形为等边三角形,所以,
因为平面平面,所以平面 ,
因为,所以两两垂直,
所以,如下图,以为坐标原点,分别以所在的直线为轴,轴 ,轴,
建立空间直角坐标系,则,
,
因为点是的中点,所以,
平面的一个法向量为,
,显然 与不共线,
所以与平面不垂直,所以A不正确;
,
设平面的法向量为,则
,
令,则,
所以,
设与平面所成角为,
则,
所以,所以B正确;
三棱锥的体积为
,
所以C不正确;
设四棱锥外接球的球心为,则,
所以,
解得,即为矩形对角线的交点,
所以四棱锥外接球的半径为3,
设四棱锥外接球的内接正四面体的棱长为,
将四面体拓展成正方体,其中正四面体棱为正方体面的对角线,
故正方体的棱长为,所以,得,
所以正四面体的表面积为,所以D正确.
故选:BD
【点睛】
此题考查线面垂直,线面角,棱锥的体积,棱锥的外接球等知识,综合性强,考查了计算能力,属于较难题.
9.
【分析】
先分析若,,,时,点在图中的点,
由,,,可得,,,可以得出点在三棱锥内,计算三棱锥的体积即可求解.
【详解】
因为,,,,
当,,时,点在图中的点,
因为,当,时,
同理,,
,,,
由知点在内,
而,,,,
所以点在三棱锥内,
且,,,
过作平面的垂线,垂足为,
由三余弦定理可得:,即,
所以,所以,
,
所以三棱锥的体积为,
故答案为:.
【点睛】
关键点点睛:本题解题的关键是由可得是以为邻边所成的平行六面体的体对角线,关键点是分析出,,,得出点在三棱锥内.
10.
【分析】
本题首先可以绘出正四棱锥的图像并构建空间直角坐标系,然后设,根据异面直线与所成角为计算出,再然后设点到底面的距离为以及点到底面的距离为并根据三角形相似的性质得出,最后根据三棱锥的体积公式即可得出结果.
【详解】
如图,设点为底面正方形的中心,取的中点,
以为坐标原点,分别以直线、、为、、轴建立空间直角坐标系,
易知,,,,
,,,
设(且),
则,
由,
整理得,解得(舍去),
故,且点在射线上,
设点到底面的距离为,点到底面的距离为,
因为,,
所以,,
故答案为:.
【点睛】
本题考查几何体体积的求法,考查异面直线所成角的灵活应用,考查三棱锥的体积公式,考查运算能力和空间想象能力,体现了综合性,是难题.
11.
【分析】
如图建立空间坐标系,利用长度关系明确P点坐标,借助向量夹角公式得到结果.
【详解】
,
设
∵
∴
,
故答案为:
【点睛】
本题以棱锥为背景,考查角的大小的度量,考查空间坐标法,考查空间想象能力与计算能力,属于中档题.
12.①②④
【分析】
取中点,建立合适的空间直角坐标系,利用平面几何知识求出所需点的坐标,然后将垂直关系转化我向量的数量积为,求出的长度,再利用球的体积公式和表面积公式进行判断即可得到答案.
【详解】
取中点,连接,以为坐标原点,为轴,为轴建立空间直角坐标系如图所示,
设,则,,,,,
所以,
由,是正三角形,得三棱锥为正三棱锥,
设外接球球心为,半径为,则,且轴,
所以,,
解得,
若,则,,
所以,解得:,
所以,故选项①正确;
又,所以,故选项②正确;
若,则,
所以,解得:,故选项③错误;
又,所以,故选项④正确;
故答案为:①②④.
13.(1)证明见解析,(2)
【分析】
(1)先证明四边形为菱形,即可说明,则可得出平面,由到平面的距离即为点到平面的距离,借助则可计算出结果.
(2)建立空间直角坐标系,由题意可说明,设,求出平面的法向量为,根据与所成角的余弦值可表示出直线直线与平面所成角的正弦值,即可求出其取最大值时的,则可求出点的坐标,再求出平面的法向量为,由二面角的余弦公式则可求出二面角的正弦值.
【详解】
(1)如图,连接,交于点,为的外心,
所以,
所以.
故和都为等边三角形,
即四边形为菱形,
所以且.
又平面、平面 ,
所以平面.
则到平面的距离即为点到平面的距离,记为 ,
由题意知:,
所以, .
又因为
即
解得:.
(2)因为平面,平面,平面平面=,
所以.
如图所示:以点为原点建系.则.
设,
所以.
设平面的法向量为.
则
所以直线与平面所成角的正弦值为:,
即当时直线与平面所成角取最大值.
此时,
所以,
设平面的法向量为.
则令则.
所以,即
则二面角的正弦值.
14.(1)证明见解析;(2).
【分析】
(1)根据条件,先利用线面垂直的判定定理证明AC⊥平面DEF,进而证得DE⊥AC;
(2)先用等积法算出DG,进而算出GF,然后建立空间直角坐标系,通过空间向量线面角的求法求得答案.
【详解】
(1)取AC的中点F,连接DF,CE,EF,
则△DAC,△EAC均为等腰直角三角形.
∴AC⊥DF,AC⊥EF,∵DF∩EF=F,∴AC⊥平面DEF,又DE 平面DEF,∴DE⊥AC.
(2)连接GA,GC.
∵DG⊥平面ABC,而GA 平面ABC,GC 平面ABC,∴DG⊥GA,DG⊥GC,
又DA=DC,∴GA=GC,∴G在AC的垂直平分线上,又EA=EC,∴E在AC的垂直平分线上,∴EG垂直平分AC,又F为AC的中点,∴E,F,G共线.
由AB=2AD=2DC=6,知△ABC为等腰直角三角形,
∴S△ABC=×AC×BC=×6×6=18,∴VDABC=×S△ABC×DG=×18×DG=12,
∴DG=2.
在等腰直角三角形DAC和等腰直角三角形EAC中,EF=DF=AC=3,
在Rt△DGF中,GF=.
过G作平行于AC的直线MN,以G为坐标原点,GM为x轴,GE为y轴,GD为z轴,建立如图所示的空间直角坐标系,
则A(3,-1,0),B(-3,5,0),C(-3,-1,0),D(0,0,2).
∴=(-3,5,-2).
设平面DAC的法向量为=(x,y,z),
又=(3,-1,-2),=(-3,-1,-2),
由,得:,令z=1,得:,
于是,,
故DB与平面DAC所成角的余弦值为.
15.(1)证明见解析;(2)
【分析】
(1)连结,交于点,连结,由中位线性质可得,利用线面平行的判定定理可得平面;
(2)易得,由线面垂直的性质定理可得面,,以为原点,以为轴,建立空间直角坐标系,利用空间向量求二面角的余弦值即可解.
【详解】
证明:(1)连结,交于点,连结,
由底面为菱形,为中点,
∵为中点,∴.
又面,面,∴面.
(2)∵为正三角形,为的中点,∴.
又∵面面,∴面,
又底面菱形,,为线段中点,
以为原点,以为轴,建立空间直角坐标系,则,,
,,,则
又,即,可得,
,
设平面的法向量为,则
,令,则
由面,所以平面的法向量为,
所以
所以二面角的正弦值为
【点睛】
方法点睛:本题考查线面平行的判定定理及面面垂直的性质定理,及面面角的求法,利用空间向量求立体几何常考查的夹角:
设直线的方向向量分别为,平面的法向量分别为,则
①两直线所成的角为(),;
②直线与平面所成的角为(),;
③二面角的大小为(),
16.(1)证明见解析;(2).
【分析】
(1)取的中点,连结,,证明平面平面,再用面面平行的性质定理证明即可;
(2)作出直线与平面所成角的平面角,通过最大角为,确定长度,建立空间直角坐标系,用向量法计算二面角余弦值.
【详解】
(1)证明:取的中点,连结,,
因为,分别为,的中点,
所以,
又因为平面,平面,
所以平面,
同理,平面,
又因为,
所以平面平面,
又因为平面,
所以平面.
(2)因为平面平面,,
所以平面,
所以即为直线与平面所成的角,
且,
当最小,即为中点时,,
此时最大为,
又因为,
所以,所以.
取的中点,连结,,
易知平面,
因为且,
所以四边形为平行四边形,
所以,
以为坐标原点,的方向为轴正方向,建立如图所示的空间直角坐标系.
则,,,,,,,,
设为平面的法向量,
则,
即
可取.
设平面的法向量为,
所以,
所以平面与平面所成锐二面角的余弦值为.
【点睛】
求直线与平面所成的角的一般步骤:
①找直线与平面所成的角,即通过找直线在平面上的射影来完成;
②计算,要把直线与平面所成的角转化到一个三角形中求解.
答案第1页,共2页
答案第1页,共2页
