人教A版2019选择性必修第一册第一章数学尖子生同步培优题典(3)(困难)word版含答案
文档属性
| 名称 | 人教A版2019选择性必修第一册第一章数学尖子生同步培优题典(3)(困难)word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-31 12:33:06 | ||
图片预览



文档简介
人教A版2019选择性必修第一册第一章数学尖子生同步培优题典(3)
第I卷(选择题)
请点击修改第I卷的文字说明
一、单选题
1.如图,在棱长为的正方体中,点是平面内一个动点,且满足,则直线与直线所成角的取值范围为( ) (参考数据:
A., B.,
C., D.,
2.已知正方体的棱长为3,为棱上的靠近点的三等分点,点在侧面上运动,当平面与平面和平面所成的角相等时,则的最小值为( )
A. B. C. D.
3.如图,在圆锥中,,是上的动点,是的直径,,是的两个三等分点,,记二面角,的平面角分别为,,若,则的最大值是( )
A. B. C. D.
二、多选题
4.如图,四边形是边长为的正方形,点、分别为线段、上的动点,,将翻折成,且平面平面,下列说法正确的是( )
A.存在点,使
B.当点为中点时,三棱锥的外接球半径为
C.三棱锥与三棱锥体积之和的最大值为
D.存在点,使平面与平面的夹角的大小为
5.已知梯形,,,,是线段上的动点;将沿着所在的直线翻折成四面体,翻折的过程中下列选项中正确的是( )
A.不论何时,与都不可能垂直
B.存在某个位置,使得平面
C.直线与平面所成角存在最大值
D.四面体的外接球的表面积的最小值为
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
6.如图,在长方体中,,点为线段上的动点(包含线段端点),则下列结论正确的__________.
①当时,平面;
②当时,平面;
③的最大值为;
④的最小值为.
7.将直角三角形沿斜边上的高折成的二面角,已知直角边,那么下面说法正确的是_________.
(1) 平面平面 (2)四面体的体积是
(3)二面角的正切值是 (4)与平面所成角的正弦值是
8.如图,圆柱的底面半径为1,高为2,平面是轴截面,点,分别是圆弧,的中点,在劣弧上(异于,),,,在平面的同侧,记二面角,的大小分别为,,则的取值范围为______.
9.已知单位向量两两的夹角均为(,且),若空间向量满足,,则有序实数组称为向量在“仿射”坐标系(O为坐标原点)下的“仿射”坐标,记作,有下列命题:
①已知,,则;
②已知,,其中,则当且仅当时,向量的夹角取得最小值;
③已知,,则;
④已知,,,则三棱锥的表面积.
其中真命题为________(写出所有真命题的序号).
四、解答题
10.如图,已知四边形由和拼接而成,其中,,,,将沿着折起.
(1)若,求异面直线与所成角的余弦值;
(2)当四面体的表面积的最大时,求二面角的余弦值.
11.如图1,在边长为2的正方形ABCD中,P为CD中点,分别将△PAD, △PBC沿 PA,PB所在直线折叠,使点C与点D重合于点O,如图2.在三棱锥P-OAB中,E为 PB中点.
(Ⅰ)求证:PO⊥AB;
(II)求直线BP与平面POA所成角的正弦值;
(Ⅲ)求二面角P-AO-E的大小.
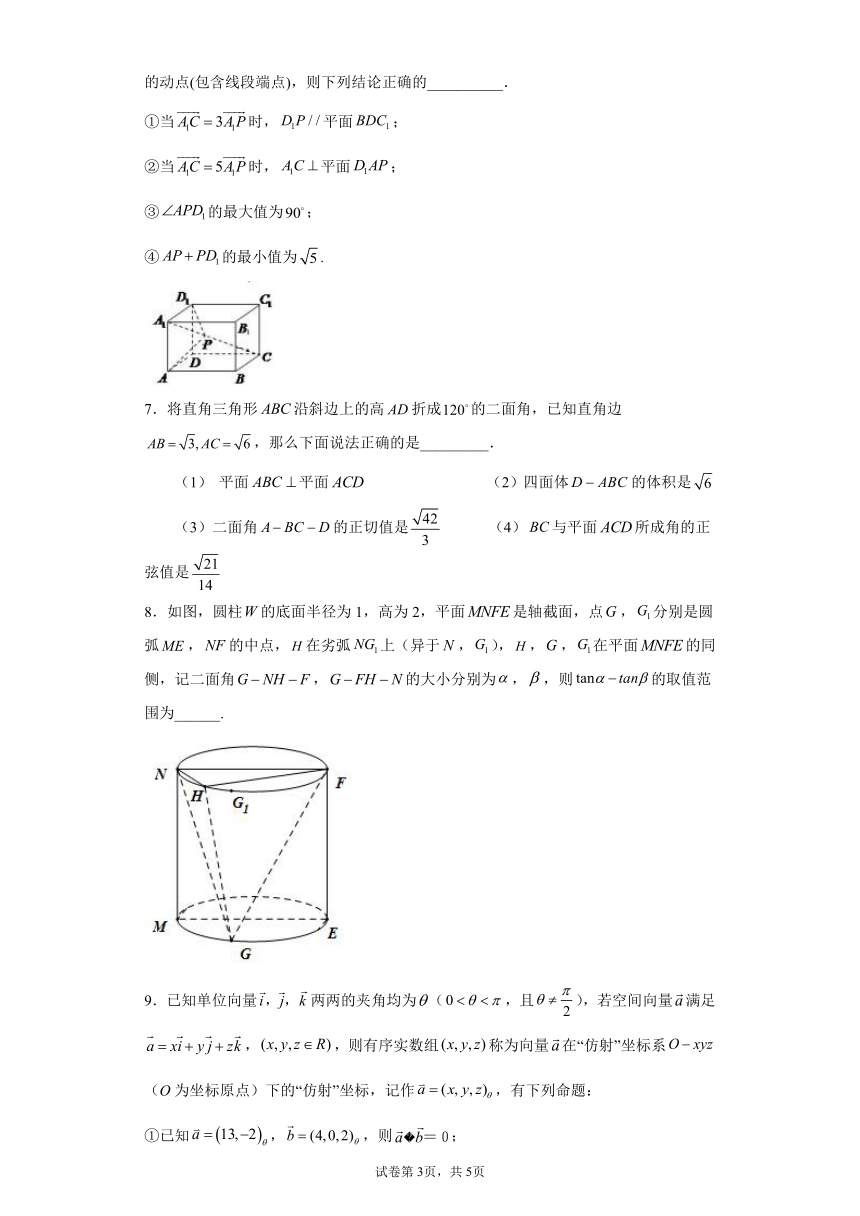
12.如图1,在△中,,分别为,的中点,为的中点,,.将△沿折起到△的位置,使得平面平面,如图2.
(1)求证:;
(2)求直线和平面所成角的正弦值;
(3)线段上是否存在点,使得直线和所成角的余弦值为?若存在,求出的值;若不存在,说明理由.
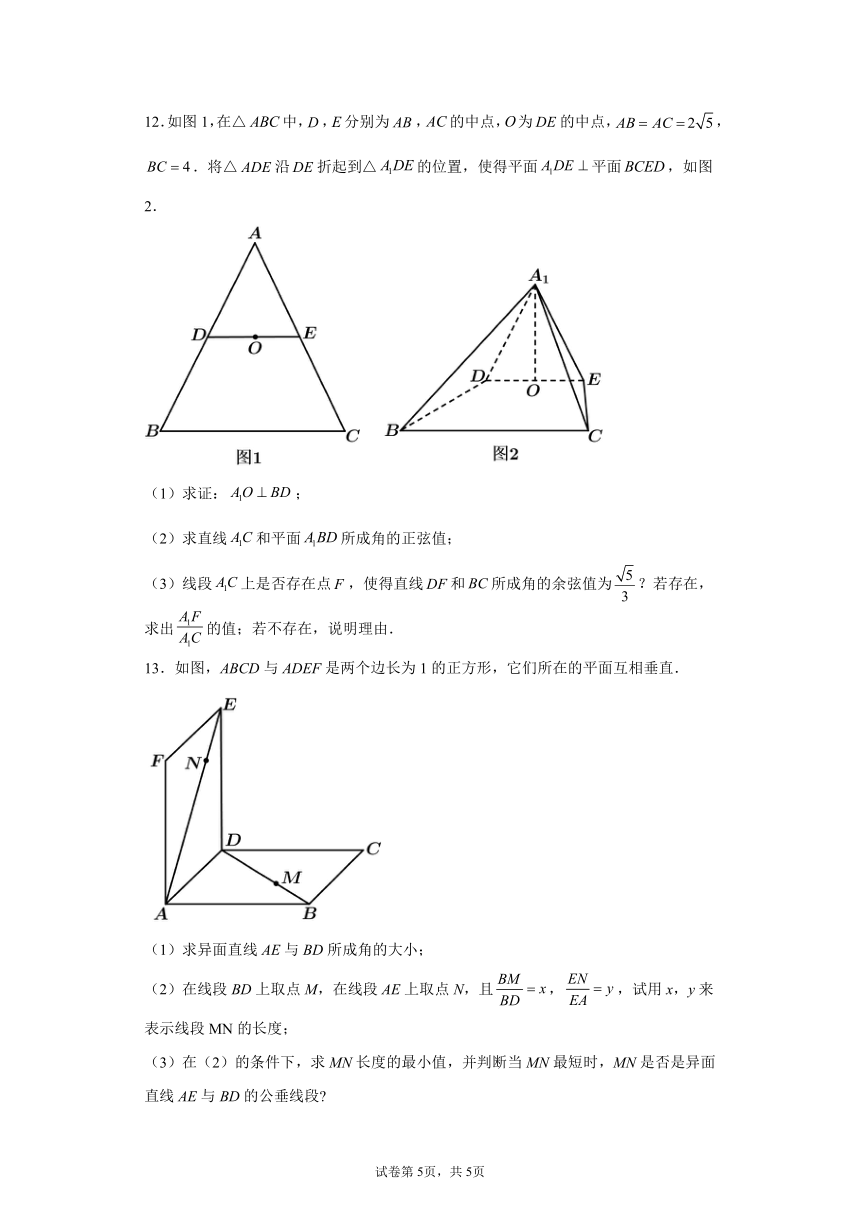
13.如图,ABCD与ADEF是两个边长为1的正方形,它们所在的平面互相垂直.
(1)求异面直线AE与BD所成角的大小;
(2)在线段BD上取点M,在线段AE上取点N,且,,试用x,y来表示线段MN的长度;
(3)在(2)的条件下,求MN长度的最小值,并判断当MN最短时,MN是否是异面直线AE与BD的公垂线段
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
【分析】
取的中点,作点在平面内的投影,过作交于点,连结、,以为坐标原点,分别以、、所在直线为、、轴建立空间直角坐标系,设,,,利用求出的关系,然后根据的范围求角的范围.
【详解】
解:取的中点,作点在平面内的投影,过作交于点,连结、,以为坐标原点,分别以、、所在直线为、、轴建立空间直角坐标系如图,
根据题意,得,0,,,0,,,,,,,,
设,,,
则,,,,,,,0,,
,
,
,,
记为直线与直线所成的角,则即为直线与直线所成的角,
,
点的轨迹在平面内是以为圆心,为半径的圆,
,,
又为锐角或直角,,
,则
直线与直线所成角的取值范围为,,
故选:B.
2.A
【分析】
作出过且与平面和平面所成角相等的截面,则P位于截面与平面的交线上,进而求得答案.
【详解】
如图1,为棱上靠近的三等分点,由正方体的对称性可知平面与平面和平面所成角相等,取棱AB上靠近B的三等分点E,取棱DC上的三等分点N,M,容易证明:,则共面,即平面与平面和平面所成角相等,于是点P在线段FN上.
如图2,过点作垂直于FN于,容易知道当P位于时,最小.
如图3,由勾股定理可以求得,由等面积法,
.
故选:A.
【点睛】
对于动点问题,通常做法是先找到动点的轨迹,以本题为例就是先作出与平面和平面所成角相等的截面,从而找到截面与的交线,做题时要充分利用图形的特征,平常注意总结截面的做法.
3.B
【分析】
设底面圆的半径为,,以所在直线为轴,以垂直于所在直线为轴,以所在直线为轴建立空间直角坐标系,写出各个点的坐标.利用法向量求得二面角与夹角的余弦值.结合即可求得的取值范围,即可得的最大值.
【详解】
设底面圆的半径为,,以所在直线为轴,以垂直于所在直线为轴,以所在直线为轴建立空间直角坐标系,如下图所示:
则由
可得,
,是的两个三等分点
则
所以
设平面的法向量为
则,代入可得
化简可得
令,解得
所以
平面的法向量为
由图可知, 二面角的平面角为锐二面角,所以二面角的平面角满足
设二面角的法向量为
则代入可得
化简可得
令,解得
所以
平面的法向量为
由图可知, 二面角的平面角为锐二面角,所以二面角的平面角满足
由二面角的范围可知
结合余弦函数的图像与性质可知
即
化简可得,且
所以
所以的最大值是
故选:B
【点睛】
本题考查了空间直角坐标系在求二面角中的综合应用,根据题意建立合适的空间直角坐标系,求得平面的法向量,即可求解.本题含参数较多,化简较为复杂,属于难题.
4.BCD
【分析】
以点为坐标原点,、所在直线分别为、轴建立空间直角坐标系,利用空间向量法可判断A选项的正误;计算出三棱锥的外接球半径,可判断B选项的正误;利用锥体的体积公式可判断C选项的正误;利用空间向量法结合零点存在定理可判断D选项的正误.
【详解】
对于A选项,以点为坐标原点,、所在直线分别为、轴建立如下图所示的空间直角坐标系,
过点在平面内作,连接,
由已知可得,,,,
故,则,即,且,
因为平面平面,平面平面,平面,
平面,
设,,则,,
因为,则,
,易得,
则点、、,
,
,
若存在点,使得,
,
化简可得,即,则,
这与矛盾,故不存在点,使得,①错;
对于B选项,当点为的中点时,则点为的中点,且,,
,
取的中点,连接、,则,,
且,,
因为,平面平面,平面平面,平面,
平面,同理可证平面,
所以,三棱锥的外接球球心在直线上,设球的半径为,
由勾股定理得,即,解得,B对;
对于C选项,,
由A选项可知,平面,
,
因为,则,令,
则,函数在上单调递增,则,
所以,C对;
对于D选项,设平面的法向量为,
,,
则,
取,可得,
易知平面的一个法向量为,
因为,
令,
可得,
即,
所以
,
令,令,
易知函数在上连续,因为,,
由零点存在定理可知,存在,使得,
因此,存在点,使平面与平面的夹角的大小为,D对.
故选:BCD.
【点睛】
方法点睛:解决与球相关的切、接问题,其通法是作出截面,将空间几何问题转化为平面几何问题求解,其解题思维流程如下:
(1)定球心:如果是内切球,球心到切点的距离相等且为球的半径;如果是外接球,球心到接点的距离相等且为半径;
(2)作截面:选准最佳角度做出截面(要使这个截面尽可能多的包含球、几何体的各种元素以及体现这些元素的关系),达到空间问题平面化的目的;
(3)求半径下结论:根据作出截面中的几何元素,建立关于球的半径的方程,并求解.
5.AD
【分析】
利用反证法可判断AB选项的正误;分别取、的中点、,连接、,以点为坐标原点,、所在直线分别为、轴建立空间直角坐标系,利用空间向量法可判断C选项的正误;设四面体的外接球心为,求出四面体外接球半径的最小值,可判断D选项的正误.
【详解】
对于A选项,在梯形中,,,,
,且,则,
因为,由余弦定理可得,
,,
若,且,平面,
平面,,事实上,矛盾,
故不论何时,与都不可能垂直,A选项正确;
对于B选项,若平面,平面,则,
所以,,而,,即,
则、、无法构成三角形,不合乎题意,B选项错误;
对于C选项,分别取、的中点、,连接、,则,
,,则,
,为的中点,则,
,故平面,
以点为坐标原点,、所在直线分别为、轴建立如下图所示的空间直角坐标系,
设,则、、、,,
设三棱锥的球心为,
由可得,解得,
设三棱锥的外接球半径为,则,当且仅当时,等号成立,
因此,四面体的外接球的表面积的最小值为,D选项正确.
对于C选项,设,
,
易知平面的一个法向量为,
,
而,
即当时,无最大值,进而可知直线与平面所成角无最大值,C选项错误.
故选:AD.
【点睛】
方法点睛:解决与球相关的切、接问题,其通法是作出截面,将空间几何问题转化为平面几何问题求解,其解题思维流程如下:
(1)定球心:如果是内切球,球心到切点的距离相等且为球的半径;如果是外接球,球心到接点的距离相等且为半径;
(2)作截面:选准最佳角度做出截面(要使这个截面尽可能多的包含球、几何体的各种元素以及体现这些元素的关系),达到空间问题平面化的目的;
(3)求半径下结论:根据作出截面中的几何元素,建立关于球的半径的方程,并求解.
6.①②
【详解】
以为坐标原点建立空间直角坐标系,则,,设,.对于①,当,即,解得,,设平面的法向量为,则由,解得,由于,所以平面成立.对于②,当时,即,解得,由可知平面成立.对于③,设,即,解得,由,其分子化简得,当时,,故的最大值可以为钝角,③错误.对于④,根据③计算的数据, ,,在对称轴,即时取得最小值为,故④错误.
点睛:本题主要考查空间点线面的位置关系,考查利用向量法证明线面平面,线面垂直的方法,考查利用向量法求角度的最大值和线段长的最小值的方法.由于题目所给几何体是长方体,要验证线面关系,用向量法最快,建立空间直角坐标系后,利用直线的方向向量和平面的法向量垂直,证明线面平行,利用直线的方向向量和平面内两个相交的向量垂直证明线面垂直.
7.(3)(4)
【分析】
画出图像,由图像判断(1)是否正确;计算的体积来判断(2)是否正确;依题意建立空间直角坐标系,利用空间向量的方法判断(3),(4)是否正确.
【详解】
画出图像如下图所示,由图可知(1)的判断显然错误.由于,故是二面角的平面角且平面,故.过作交的延长线于,由于,故是三棱锥的高.在原图中,,,,,,所以,故(2)错误.以为坐标原点,分别为轴建立空间直角坐标系.,,设平面的法向量为,则,令,则,即.平面的法向量是.设二面角的平面角为,由图可知为锐角,故,则其正切值为.故(3)判断正确.平面的法向量为,,设直线和平面所成的角为,则,故(4)判断正确.综上所述,正确的有(3),(4).
【点睛】
本小题主要考查折叠问题,考查空间面面垂直的判断,考查锥体体积计算,考查二面角的计算以及线面角的计算,属于中档题.
8.
【分析】
以点为坐标原点,分别以为轴建立空间直角坐标系,设,且,设平面的法向量,求出,设平面的法向量,求出,设平面的法向量为,利用向量夹角公式可得,可得,由,可得,代入中整理可得答案
【详解】
解:以点为坐标原点,分别以为轴建立空间直角坐标系,
所以,
设,且,
设平面的法向量,
由,得,得
设平面的法向量,
由,得,得
设平面的法向量为,则
,
所以,
,
所以,
所以
故答案为:
【点睛】
此题考二面角的余弦值的求法,向量夹角公式,数量积运算性质,考查了推理能力和计算能力,属于难题.
9.②③
【分析】
①利用定义表示与,并利用空间向量数量积的运算律和定义来进行验证;
②作出图形,设,,结合图形得出当的面积取最小值时与的夹角最小,从而判断结论的正误;
③利用“仿射”坐标的定义,结合空间向量加法的运算律来进行验证;
④根据“仿射”坐标的定义判断出三棱锥是棱长为的正四面体,于此可得出该三棱锥的表面积.
【详解】
①由定义可得
,
∵,,,故①错误;
②如图,设,,则点在平面上,点在轴上,
由图易知当时,取得最小值,即向量与的夹角取得最小值,故②正确;③根据“仿射”坐标的定义可得
,故③正确;
④由已知可知三棱锥为正四面体,棱长为,其表面积为,即④错误.
故答案为②③.
【点睛】
本题考查空间向量的新定义,在验证各命题时要严格根据题中定义来理解,结合空间向量加减法以及数量积的运算律来计算,考查推理能力,属于难题.
10.(1);(2)
【分析】
(1)设异面直线与所成角为,利用,结合向量线性运算和数量积运算,求得异面直线所成角的余弦值.
(2)建立空间直角坐标系,用二面角的三角函数值,表示出点的坐标. 由于三角形和三角形的面积为定值,故要使四面体的表面积取得最大值,则需取得最大值.求得表达式,利用最值的求法,求得取得最大值,以及此时二面角的余弦值.
【详解】
依题意可知.
(1)由于,,,,所以,.设异面直线与所成角为,则.即异面直线与所成角的余弦值为.
(2)由于三角形和三角形的面积为定值,故要使四面体的表面积取得最大值,则需取得最大值.
设是的中点,过作平面,以分别为轴建立空间直角坐标系.在沿着折起的过程中,,,所以是二面角的平面角,设,则,,所以,,,,结合向量法表示三角形面积以及柯西不等式有:
.当且仅当,即时,取得最大值.所以当四面体的表面积的最大时,二面角的余弦值为.
【点睛】
本小题主要考查利用空间向量法计算异面直线所成的角,考查利用空间向量法计算二面角,考查几何体表面积最值的求法,考查化归与转化的数学思想方法,考查运算求解能力,属于难题.
11.(Ⅰ)见解析;(Ⅱ). (Ⅲ).
【分析】
第一问利用几何体的特征可以得出相应的线线垂直,之后利用线面垂直的判定定理和性质得出所要的结果;第二问建立空间直角坐标系,利用空间向量求得线面角的正弦值;第三问利用面的法向量所成角的余弦值求得角的大小,最后确定出二面角的大小.
【详解】
(Ⅰ)在正方形中,为中点,,,
所以在三棱锥中,,.
因为,所以平面.
因为平面,所以.
(Ⅱ)取AB中点F,连接OF,取AO中点M,连接BM.
过点O作AB的平行线OG.
因为PO⊥平面OAB,所以PO⊥OF,PO⊥OG.
因为OA=OB,F为AB的中点,
所以OF⊥AB. 所以OF⊥OG.
如图所示,建立空间直角坐标系O-xyz.
A,B,P,M(,,0).
因为BO=BA,M为OA的中点,所以BM⊥OA.
因为PO⊥平面OAB,PO 平面POA,所以平面POA⊥平面OAB.
因为平面POA∩平面OAB=OA,BM 平面OAB,
所以BM⊥平面POA.
因为=(,-,0).所以平面POA的法向量m=.
=(1,-,1).
设直线BP与平面POA所成角为α,
则.
所以直线BP与平面POA所成角的正弦值为.
(Ⅲ)由(Ⅱ)知,,.
设平面的法向量为,则有
即
令,则,. 即.
所以.
由题知二面角P-AO-E为锐角,所以它的大小为.
12.(1)见解析;(2);(3)
【详解】
试题分析:第一问根据等腰三角形的特征,可以得出,再结合面面垂直的性质定理,可以得出平面,再根据线面垂直的性质,可以得出以 ,之后根据面面垂直的性质和线面垂直的性质得出结果;第二问根据题中的条件,建立空间直角坐标系,利用空间向量求得结果;第三问关于是否存在类问题,都是假设其存在,结合向量所成角的余弦值求得结果.
(Ⅰ)因为在△中,,分别为,的中点,
所以 ,.
所以,又为的中点,
所以 .
因为平面平面,且平面,
所以 平面,
所以 .
(Ⅱ)取的中点,连接,所以.
由(Ⅰ)得,.
如图建立空间直角坐标系.
由题意得,,,,.
所以,,.
设平面的法向量为,
则即
令,则,,所以.
设直线和平面所成的角为,
则.
所以 直线和平面所成角的正弦值为.
(Ⅲ)线段上存在点适合题意.
设,其中.
设,则有,
所以,从而,
所以,又,
所以.
令,
整理得.
解得,舍去.
所以线段上存在点适合题意,且.
方法点睛:该题属于典型的立体几何问题,第一问证明线线垂直,需要将空间关系都理清,把握住线线垂直、线面垂直、面面垂直的关系,即可得出结果;第二问求的是线面角的正弦值,正好是直线的方向向量与平面的法向量所成角的余弦值的绝对值;第三问属于是否存在类问题,在解题的过程中,需要我们先假设其存在,按照题的条件进行求解,如果推出矛盾,就是不存在.
13.
(1)
(2),
(3),MN是异面直线AE与BD的公垂线段
【分析】
(1)利用,可知为所求角,进而得解;
(2)以D为原点,建立空间直角坐标系,求出的坐标,利用向量的模长公式,即可表示线段MN的长度;
(3)求出的最小值,利用向量验证MN是否与AE,BD垂直.
(1)
补全正方体,连接,,由正方体的性质知,
则异面直线AE与BD所成角,即为直线与BD所成角
又为等边三角形,故
所以异面直线AE与BD所成角的大小为.
(2)
如图,以D为原点,分别为轴建立空间直角坐标系,
由,,知,,其中
,
则,
(3)
当,要求的最小值
即求的最小值
由
,
当且仅当时,等号成立,
,,
又,,,
则,,
,,
所以MN是异面直线AE与BD的公垂线段.
答案第1页,共2页
答案第1页,共2页
第I卷(选择题)
请点击修改第I卷的文字说明
一、单选题
1.如图,在棱长为的正方体中,点是平面内一个动点,且满足,则直线与直线所成角的取值范围为( ) (参考数据:
A., B.,
C., D.,
2.已知正方体的棱长为3,为棱上的靠近点的三等分点,点在侧面上运动,当平面与平面和平面所成的角相等时,则的最小值为( )
A. B. C. D.
3.如图,在圆锥中,,是上的动点,是的直径,,是的两个三等分点,,记二面角,的平面角分别为,,若,则的最大值是( )
A. B. C. D.
二、多选题
4.如图,四边形是边长为的正方形,点、分别为线段、上的动点,,将翻折成,且平面平面,下列说法正确的是( )
A.存在点,使
B.当点为中点时,三棱锥的外接球半径为
C.三棱锥与三棱锥体积之和的最大值为
D.存在点,使平面与平面的夹角的大小为
5.已知梯形,,,,是线段上的动点;将沿着所在的直线翻折成四面体,翻折的过程中下列选项中正确的是( )
A.不论何时,与都不可能垂直
B.存在某个位置,使得平面
C.直线与平面所成角存在最大值
D.四面体的外接球的表面积的最小值为
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
6.如图,在长方体中,,点为线段上的动点(包含线段端点),则下列结论正确的__________.
①当时,平面;
②当时,平面;
③的最大值为;
④的最小值为.
7.将直角三角形沿斜边上的高折成的二面角,已知直角边,那么下面说法正确的是_________.
(1) 平面平面 (2)四面体的体积是
(3)二面角的正切值是 (4)与平面所成角的正弦值是
8.如图,圆柱的底面半径为1,高为2,平面是轴截面,点,分别是圆弧,的中点,在劣弧上(异于,),,,在平面的同侧,记二面角,的大小分别为,,则的取值范围为______.
9.已知单位向量两两的夹角均为(,且),若空间向量满足,,则有序实数组称为向量在“仿射”坐标系(O为坐标原点)下的“仿射”坐标,记作,有下列命题:
①已知,,则;
②已知,,其中,则当且仅当时,向量的夹角取得最小值;
③已知,,则;
④已知,,,则三棱锥的表面积.
其中真命题为________(写出所有真命题的序号).
四、解答题
10.如图,已知四边形由和拼接而成,其中,,,,将沿着折起.
(1)若,求异面直线与所成角的余弦值;
(2)当四面体的表面积的最大时,求二面角的余弦值.
11.如图1,在边长为2的正方形ABCD中,P为CD中点,分别将△PAD, △PBC沿 PA,PB所在直线折叠,使点C与点D重合于点O,如图2.在三棱锥P-OAB中,E为 PB中点.
(Ⅰ)求证:PO⊥AB;
(II)求直线BP与平面POA所成角的正弦值;
(Ⅲ)求二面角P-AO-E的大小.
12.如图1,在△中,,分别为,的中点,为的中点,,.将△沿折起到△的位置,使得平面平面,如图2.
(1)求证:;
(2)求直线和平面所成角的正弦值;
(3)线段上是否存在点,使得直线和所成角的余弦值为?若存在,求出的值;若不存在,说明理由.
13.如图,ABCD与ADEF是两个边长为1的正方形,它们所在的平面互相垂直.
(1)求异面直线AE与BD所成角的大小;
(2)在线段BD上取点M,在线段AE上取点N,且,,试用x,y来表示线段MN的长度;
(3)在(2)的条件下,求MN长度的最小值,并判断当MN最短时,MN是否是异面直线AE与BD的公垂线段
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
【分析】
取的中点,作点在平面内的投影,过作交于点,连结、,以为坐标原点,分别以、、所在直线为、、轴建立空间直角坐标系,设,,,利用求出的关系,然后根据的范围求角的范围.
【详解】
解:取的中点,作点在平面内的投影,过作交于点,连结、,以为坐标原点,分别以、、所在直线为、、轴建立空间直角坐标系如图,
根据题意,得,0,,,0,,,,,,,,
设,,,
则,,,,,,,0,,
,
,
,,
记为直线与直线所成的角,则即为直线与直线所成的角,
,
点的轨迹在平面内是以为圆心,为半径的圆,
,,
又为锐角或直角,,
,则
直线与直线所成角的取值范围为,,
故选:B.
2.A
【分析】
作出过且与平面和平面所成角相等的截面,则P位于截面与平面的交线上,进而求得答案.
【详解】
如图1,为棱上靠近的三等分点,由正方体的对称性可知平面与平面和平面所成角相等,取棱AB上靠近B的三等分点E,取棱DC上的三等分点N,M,容易证明:,则共面,即平面与平面和平面所成角相等,于是点P在线段FN上.
如图2,过点作垂直于FN于,容易知道当P位于时,最小.
如图3,由勾股定理可以求得,由等面积法,
.
故选:A.
【点睛】
对于动点问题,通常做法是先找到动点的轨迹,以本题为例就是先作出与平面和平面所成角相等的截面,从而找到截面与的交线,做题时要充分利用图形的特征,平常注意总结截面的做法.
3.B
【分析】
设底面圆的半径为,,以所在直线为轴,以垂直于所在直线为轴,以所在直线为轴建立空间直角坐标系,写出各个点的坐标.利用法向量求得二面角与夹角的余弦值.结合即可求得的取值范围,即可得的最大值.
【详解】
设底面圆的半径为,,以所在直线为轴,以垂直于所在直线为轴,以所在直线为轴建立空间直角坐标系,如下图所示:
则由
可得,
,是的两个三等分点
则
所以
设平面的法向量为
则,代入可得
化简可得
令,解得
所以
平面的法向量为
由图可知, 二面角的平面角为锐二面角,所以二面角的平面角满足
设二面角的法向量为
则代入可得
化简可得
令,解得
所以
平面的法向量为
由图可知, 二面角的平面角为锐二面角,所以二面角的平面角满足
由二面角的范围可知
结合余弦函数的图像与性质可知
即
化简可得,且
所以
所以的最大值是
故选:B
【点睛】
本题考查了空间直角坐标系在求二面角中的综合应用,根据题意建立合适的空间直角坐标系,求得平面的法向量,即可求解.本题含参数较多,化简较为复杂,属于难题.
4.BCD
【分析】
以点为坐标原点,、所在直线分别为、轴建立空间直角坐标系,利用空间向量法可判断A选项的正误;计算出三棱锥的外接球半径,可判断B选项的正误;利用锥体的体积公式可判断C选项的正误;利用空间向量法结合零点存在定理可判断D选项的正误.
【详解】
对于A选项,以点为坐标原点,、所在直线分别为、轴建立如下图所示的空间直角坐标系,
过点在平面内作,连接,
由已知可得,,,,
故,则,即,且,
因为平面平面,平面平面,平面,
平面,
设,,则,,
因为,则,
,易得,
则点、、,
,
,
若存在点,使得,
,
化简可得,即,则,
这与矛盾,故不存在点,使得,①错;
对于B选项,当点为的中点时,则点为的中点,且,,
,
取的中点,连接、,则,,
且,,
因为,平面平面,平面平面,平面,
平面,同理可证平面,
所以,三棱锥的外接球球心在直线上,设球的半径为,
由勾股定理得,即,解得,B对;
对于C选项,,
由A选项可知,平面,
,
因为,则,令,
则,函数在上单调递增,则,
所以,C对;
对于D选项,设平面的法向量为,
,,
则,
取,可得,
易知平面的一个法向量为,
因为,
令,
可得,
即,
所以
,
令,令,
易知函数在上连续,因为,,
由零点存在定理可知,存在,使得,
因此,存在点,使平面与平面的夹角的大小为,D对.
故选:BCD.
【点睛】
方法点睛:解决与球相关的切、接问题,其通法是作出截面,将空间几何问题转化为平面几何问题求解,其解题思维流程如下:
(1)定球心:如果是内切球,球心到切点的距离相等且为球的半径;如果是外接球,球心到接点的距离相等且为半径;
(2)作截面:选准最佳角度做出截面(要使这个截面尽可能多的包含球、几何体的各种元素以及体现这些元素的关系),达到空间问题平面化的目的;
(3)求半径下结论:根据作出截面中的几何元素,建立关于球的半径的方程,并求解.
5.AD
【分析】
利用反证法可判断AB选项的正误;分别取、的中点、,连接、,以点为坐标原点,、所在直线分别为、轴建立空间直角坐标系,利用空间向量法可判断C选项的正误;设四面体的外接球心为,求出四面体外接球半径的最小值,可判断D选项的正误.
【详解】
对于A选项,在梯形中,,,,
,且,则,
因为,由余弦定理可得,
,,
若,且,平面,
平面,,事实上,矛盾,
故不论何时,与都不可能垂直,A选项正确;
对于B选项,若平面,平面,则,
所以,,而,,即,
则、、无法构成三角形,不合乎题意,B选项错误;
对于C选项,分别取、的中点、,连接、,则,
,,则,
,为的中点,则,
,故平面,
以点为坐标原点,、所在直线分别为、轴建立如下图所示的空间直角坐标系,
设,则、、、,,
设三棱锥的球心为,
由可得,解得,
设三棱锥的外接球半径为,则,当且仅当时,等号成立,
因此,四面体的外接球的表面积的最小值为,D选项正确.
对于C选项,设,
,
易知平面的一个法向量为,
,
而,
即当时,无最大值,进而可知直线与平面所成角无最大值,C选项错误.
故选:AD.
【点睛】
方法点睛:解决与球相关的切、接问题,其通法是作出截面,将空间几何问题转化为平面几何问题求解,其解题思维流程如下:
(1)定球心:如果是内切球,球心到切点的距离相等且为球的半径;如果是外接球,球心到接点的距离相等且为半径;
(2)作截面:选准最佳角度做出截面(要使这个截面尽可能多的包含球、几何体的各种元素以及体现这些元素的关系),达到空间问题平面化的目的;
(3)求半径下结论:根据作出截面中的几何元素,建立关于球的半径的方程,并求解.
6.①②
【详解】
以为坐标原点建立空间直角坐标系,则,,设,.对于①,当,即,解得,,设平面的法向量为,则由,解得,由于,所以平面成立.对于②,当时,即,解得,由可知平面成立.对于③,设,即,解得,由,其分子化简得,当时,,故的最大值可以为钝角,③错误.对于④,根据③计算的数据, ,,在对称轴,即时取得最小值为,故④错误.
点睛:本题主要考查空间点线面的位置关系,考查利用向量法证明线面平面,线面垂直的方法,考查利用向量法求角度的最大值和线段长的最小值的方法.由于题目所给几何体是长方体,要验证线面关系,用向量法最快,建立空间直角坐标系后,利用直线的方向向量和平面的法向量垂直,证明线面平行,利用直线的方向向量和平面内两个相交的向量垂直证明线面垂直.
7.(3)(4)
【分析】
画出图像,由图像判断(1)是否正确;计算的体积来判断(2)是否正确;依题意建立空间直角坐标系,利用空间向量的方法判断(3),(4)是否正确.
【详解】
画出图像如下图所示,由图可知(1)的判断显然错误.由于,故是二面角的平面角且平面,故.过作交的延长线于,由于,故是三棱锥的高.在原图中,,,,,,所以,故(2)错误.以为坐标原点,分别为轴建立空间直角坐标系.,,设平面的法向量为,则,令,则,即.平面的法向量是.设二面角的平面角为,由图可知为锐角,故,则其正切值为.故(3)判断正确.平面的法向量为,,设直线和平面所成的角为,则,故(4)判断正确.综上所述,正确的有(3),(4).
【点睛】
本小题主要考查折叠问题,考查空间面面垂直的判断,考查锥体体积计算,考查二面角的计算以及线面角的计算,属于中档题.
8.
【分析】
以点为坐标原点,分别以为轴建立空间直角坐标系,设,且,设平面的法向量,求出,设平面的法向量,求出,设平面的法向量为,利用向量夹角公式可得,可得,由,可得,代入中整理可得答案
【详解】
解:以点为坐标原点,分别以为轴建立空间直角坐标系,
所以,
设,且,
设平面的法向量,
由,得,得
设平面的法向量,
由,得,得
设平面的法向量为,则
,
所以,
,
所以,
所以
故答案为:
【点睛】
此题考二面角的余弦值的求法,向量夹角公式,数量积运算性质,考查了推理能力和计算能力,属于难题.
9.②③
【分析】
①利用定义表示与,并利用空间向量数量积的运算律和定义来进行验证;
②作出图形,设,,结合图形得出当的面积取最小值时与的夹角最小,从而判断结论的正误;
③利用“仿射”坐标的定义,结合空间向量加法的运算律来进行验证;
④根据“仿射”坐标的定义判断出三棱锥是棱长为的正四面体,于此可得出该三棱锥的表面积.
【详解】
①由定义可得
,
∵,,,故①错误;
②如图,设,,则点在平面上,点在轴上,
由图易知当时,取得最小值,即向量与的夹角取得最小值,故②正确;③根据“仿射”坐标的定义可得
,故③正确;
④由已知可知三棱锥为正四面体,棱长为,其表面积为,即④错误.
故答案为②③.
【点睛】
本题考查空间向量的新定义,在验证各命题时要严格根据题中定义来理解,结合空间向量加减法以及数量积的运算律来计算,考查推理能力,属于难题.
10.(1);(2)
【分析】
(1)设异面直线与所成角为,利用,结合向量线性运算和数量积运算,求得异面直线所成角的余弦值.
(2)建立空间直角坐标系,用二面角的三角函数值,表示出点的坐标. 由于三角形和三角形的面积为定值,故要使四面体的表面积取得最大值,则需取得最大值.求得表达式,利用最值的求法,求得取得最大值,以及此时二面角的余弦值.
【详解】
依题意可知.
(1)由于,,,,所以,.设异面直线与所成角为,则.即异面直线与所成角的余弦值为.
(2)由于三角形和三角形的面积为定值,故要使四面体的表面积取得最大值,则需取得最大值.
设是的中点,过作平面,以分别为轴建立空间直角坐标系.在沿着折起的过程中,,,所以是二面角的平面角,设,则,,所以,,,,结合向量法表示三角形面积以及柯西不等式有:
.当且仅当,即时,取得最大值.所以当四面体的表面积的最大时,二面角的余弦值为.
【点睛】
本小题主要考查利用空间向量法计算异面直线所成的角,考查利用空间向量法计算二面角,考查几何体表面积最值的求法,考查化归与转化的数学思想方法,考查运算求解能力,属于难题.
11.(Ⅰ)见解析;(Ⅱ). (Ⅲ).
【分析】
第一问利用几何体的特征可以得出相应的线线垂直,之后利用线面垂直的判定定理和性质得出所要的结果;第二问建立空间直角坐标系,利用空间向量求得线面角的正弦值;第三问利用面的法向量所成角的余弦值求得角的大小,最后确定出二面角的大小.
【详解】
(Ⅰ)在正方形中,为中点,,,
所以在三棱锥中,,.
因为,所以平面.
因为平面,所以.
(Ⅱ)取AB中点F,连接OF,取AO中点M,连接BM.
过点O作AB的平行线OG.
因为PO⊥平面OAB,所以PO⊥OF,PO⊥OG.
因为OA=OB,F为AB的中点,
所以OF⊥AB. 所以OF⊥OG.
如图所示,建立空间直角坐标系O-xyz.
A,B,P,M(,,0).
因为BO=BA,M为OA的中点,所以BM⊥OA.
因为PO⊥平面OAB,PO 平面POA,所以平面POA⊥平面OAB.
因为平面POA∩平面OAB=OA,BM 平面OAB,
所以BM⊥平面POA.
因为=(,-,0).所以平面POA的法向量m=.
=(1,-,1).
设直线BP与平面POA所成角为α,
则.
所以直线BP与平面POA所成角的正弦值为.
(Ⅲ)由(Ⅱ)知,,.
设平面的法向量为,则有
即
令,则,. 即.
所以.
由题知二面角P-AO-E为锐角,所以它的大小为.
12.(1)见解析;(2);(3)
【详解】
试题分析:第一问根据等腰三角形的特征,可以得出,再结合面面垂直的性质定理,可以得出平面,再根据线面垂直的性质,可以得出以 ,之后根据面面垂直的性质和线面垂直的性质得出结果;第二问根据题中的条件,建立空间直角坐标系,利用空间向量求得结果;第三问关于是否存在类问题,都是假设其存在,结合向量所成角的余弦值求得结果.
(Ⅰ)因为在△中,,分别为,的中点,
所以 ,.
所以,又为的中点,
所以 .
因为平面平面,且平面,
所以 平面,
所以 .
(Ⅱ)取的中点,连接,所以.
由(Ⅰ)得,.
如图建立空间直角坐标系.
由题意得,,,,.
所以,,.
设平面的法向量为,
则即
令,则,,所以.
设直线和平面所成的角为,
则.
所以 直线和平面所成角的正弦值为.
(Ⅲ)线段上存在点适合题意.
设,其中.
设,则有,
所以,从而,
所以,又,
所以.
令,
整理得.
解得,舍去.
所以线段上存在点适合题意,且.
方法点睛:该题属于典型的立体几何问题,第一问证明线线垂直,需要将空间关系都理清,把握住线线垂直、线面垂直、面面垂直的关系,即可得出结果;第二问求的是线面角的正弦值,正好是直线的方向向量与平面的法向量所成角的余弦值的绝对值;第三问属于是否存在类问题,在解题的过程中,需要我们先假设其存在,按照题的条件进行求解,如果推出矛盾,就是不存在.
13.
(1)
(2),
(3),MN是异面直线AE与BD的公垂线段
【分析】
(1)利用,可知为所求角,进而得解;
(2)以D为原点,建立空间直角坐标系,求出的坐标,利用向量的模长公式,即可表示线段MN的长度;
(3)求出的最小值,利用向量验证MN是否与AE,BD垂直.
(1)
补全正方体,连接,,由正方体的性质知,
则异面直线AE与BD所成角,即为直线与BD所成角
又为等边三角形,故
所以异面直线AE与BD所成角的大小为.
(2)
如图,以D为原点,分别为轴建立空间直角坐标系,
由,,知,,其中
,
则,
(3)
当,要求的最小值
即求的最小值
由
,
当且仅当时,等号成立,
,,
又,,,
则,,
,,
所以MN是异面直线AE与BD的公垂线段.
答案第1页,共2页
答案第1页,共2页
