安徽省安庆市第九中学2012-2013学年高一上学期期中考试数学试题(无答案)
文档属性
| 名称 | 安徽省安庆市第九中学2012-2013学年高一上学期期中考试数学试题(无答案) | 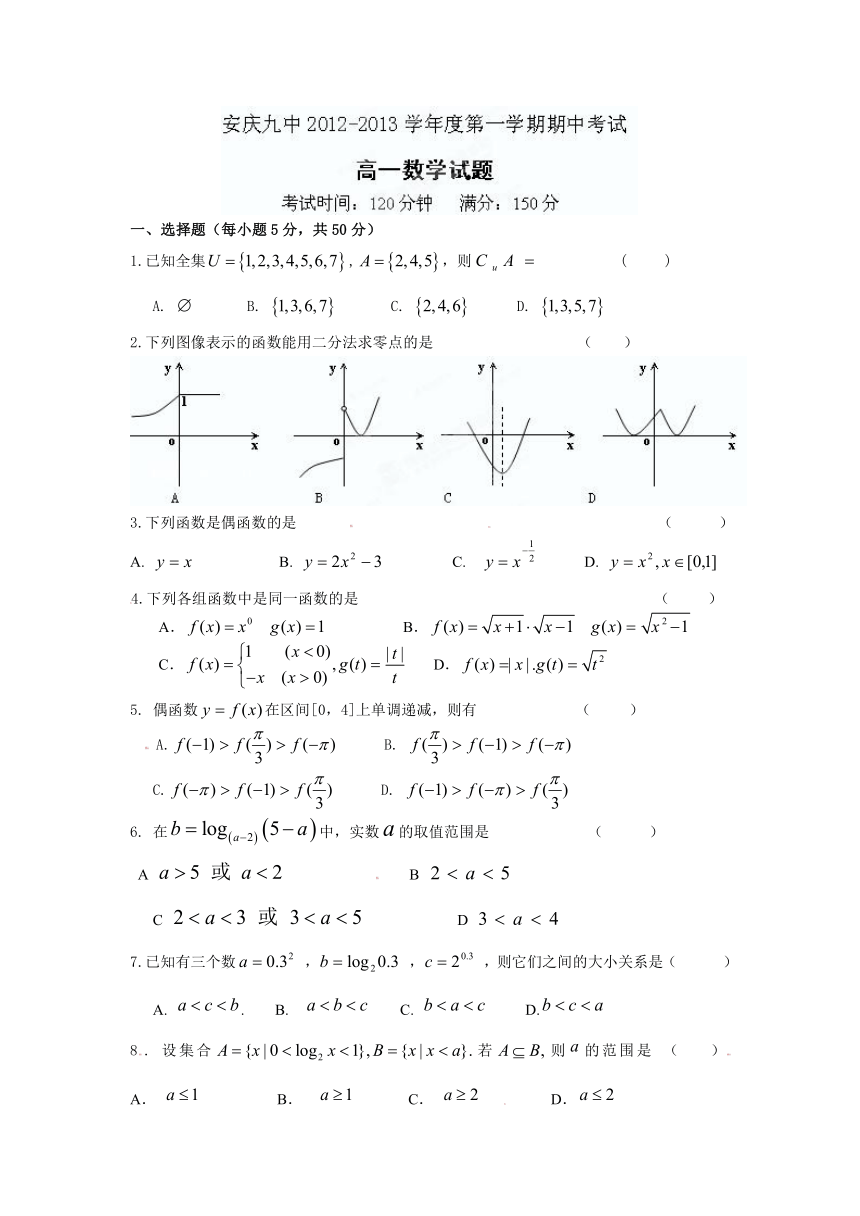 | |
| 格式 | zip | ||
| 文件大小 | 110.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-22 21:19:51 | ||
图片预览


文档简介
一、选择题(每小题5分,共50分)
1.已知全集,,则 ( )
A. B. C. D.
2.下列图像表示的函数能用二分法求零点的是 ( )
3.下列函数是偶函数的是 ( )
A. B. C. D.
4.下列各组函数中是同一函数的是 ( )
A. B.
C. D.
5. 偶函数在区间[0,4]上单调递减,则有 ( )
A. B.
C. D.
6. 在中,实数的取值范围是 ( )
A B
C D
7.已知有三个数 , , ,则它们之间的大小关系是( )
A. . B. C. D.
8. 设集合若则的范围是 ( ) A. B. C. D.
9.已知函数的图象是连续不断的,且有如下对应值表:
1
2
3
4
5
y
1
4
7
在下列区间中,函数必有零点的区间为( ).
A.(1,2) B.(3,4) C . (2,3) D. (4,5)
10.计算机成本不断降低,若每隔三年计算机价格降低,则现在价格为8100元的计算机
9年后价格可降为( )
A. 2400元 B. 900元 C. 300元 D.3600元
二、填空题:(本大题共5小题,每小题5分,共25分)
11. 8.已知函数,则=_________.
12.已知在定义域R上是减函数,且,则的取值范围是 。
13.已知幂函数的图象过点 .
14.设,,则=_________.
15、函数在[1,+∞)上为增函数,则实数的取值范围
___________________;
三、解答题(共75分)
16.化简计算(每小题5分,共10分)
已知全集,
(1)求A∩B;
(2)求;
17.(每小题5分,共10分)
(1)
(2)
18.(每小题5分,共10分)
已知。
(1)求的定义域 ;
(2)证明:为奇函数.
19.(每小题5分,共10分)
已知函数
(1)用分段函数的形式表示该函数;
(2)画出该函数的图象.
20.(每小题6分,共12分)
已知函数=,
(1)判断在区间(1,+∞)上的单调性,并用定义证明;
(2)当(- ∞,0)时,写出函数=的单调区间(不必证明).
21.(每小题6分,共12分)
(1)已知,求.
(2)已知定义在R上的奇函数,当>0时,,求f(x)的解析式 .
22、(第1小题5分,第2题6分,11分)
已知函数 ,
(1)求函数的值域;
(2)若时,函数的最小值为,求的值和函数的最大值。
同课章节目录
