2021-2022学年高一下学期数学北师大版(2019)必修第二册2.6.1第三节用余弦定理、正弦定理解三角形课件(共34张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学北师大版(2019)必修第二册2.6.1第三节用余弦定理、正弦定理解三角形课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 00:00:00 | ||
图片预览










文档简介
(共34张PPT)
2.6.1余弦定理、正弦定理
第三课时 用余弦定理、正弦定理解三角形
北师大(2019)必修2
聚焦知识目标和数学素养
1.了解三角函数是研究周期现象最重要的模型.(重点)
2.初步体会如何利用三角函数研究简单的实际问题.(难点)
1.会用正弦定理、余弦定理解决与三角形有关的几何计算问题.(数学运算、逻辑推理)
2.会用正弦定理、余弦定理解决与距离、高度、角度有关的实际问题.(数学建模、数学运算)
复习引入
在△ABC中,若角A,B,C所对的边分别是a,b,c,R为△ABC外接圆半径,则
1.正弦定理、余弦定理
定理 正弦定理 余弦定理
内容 = = =2R a2= ;
b2= ;
c2=_______________
b2+c2-2bccos A
c2+a2-2cacos B
a2+b2-2abcos C
变形 (1)a=2Rsin A,b= ,c= ; (2)sin A= ,sin B= ,sin C= ; (3)a∶b∶c= ; (4)asin B=bsin A, bsin C=csin B, asin C=csin A cos A= ;
cos B= ;
cos C=____________
2Rsin B
2Rsin C
sin A∶sin B∶sin C
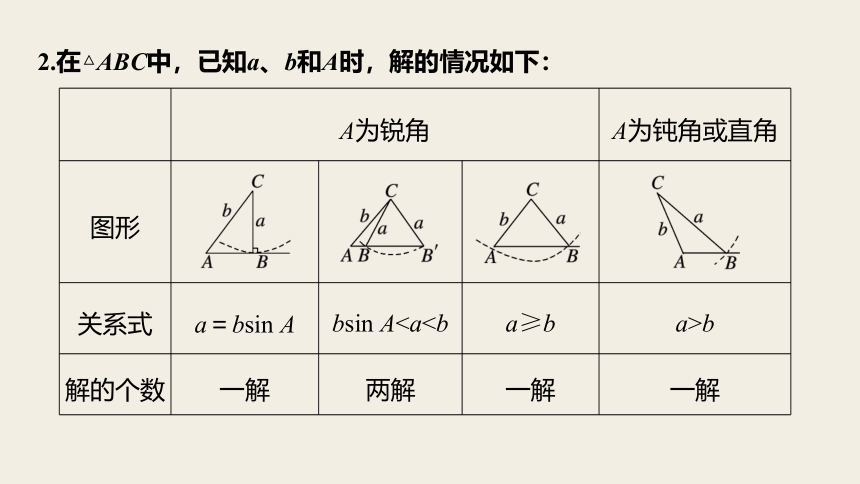
2.在△ABC中,已知a、b和A时,解的情况如下:
A为锐角 A为钝角或直角
图形
关系式 a=bsin A bsin Ab
解的个数 一解 两解 一解 一解
3.三角形常用面积公式
(1)S= a·ha(ha表示边a上的高);
(2)S= absin C= = ;
(3)S= r(a+b+c)(r为三角形内切圆半径).
acsin B
bcsin A
1.三角形内角和定理
在△ABC中,A+B+C=π;
2.三角形中的三角函数关系
(1)sin(A+B)=sin C;(2)cos(A+B)=-cos C;
3.三角形中的射影定理
在△ABC中,a=bcos C+ccos B;b=acos C+ccos A;c=bcos A+acos B.
4.三角形常用结论
解三角形及相关应用
解三角形与三角形有关的几何计算
在三角形的三条边和三个角这6个元素中,如果已知3个(至少含一边长),那么由余弦定理和正弦定理,就可以求得其他3个元素.具体情形如下:
情形1 已知两个角的大小与一条边的边长.
先由三角形内角和等于180°求出第三个角的大小,然后依据正弦定理求得另外两条边的边长.
情形2 已知两条边的边长及其夹角的大小.
先由余弦定理求出第三条边的边长,然后再由余弦定理求得第二、第三个角的大小.
情形3 已知三条边的边长.
由余弦定理求出两个角,再利用三角形内角和等于180°求出第三个角.
情形4 已知两条边的边长和其中一边对角的大小.
首先,由正弦定理求出第二条边所对角的正弦,这时,要判断是两解、一解还是无解.然后,根据三角形内角和等于180°得到第三个角的大小.最后,由余弦定理或正弦定理求得第三条边的边长.
几何计算
典例
例1.
几何计算
练习
在四边形ABCD中,已知AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,求BC的长.
解在△ABD中,设BD=x,由余弦定理,得BA2=BD2+AD2-2BD·AD·cos∠BDA
即142=x2+102-2·10x·cos 60°,
整理得x2-10x-96=0,
解得x1=16,x2=-6(舍去),所以BD=16.
由AD⊥CD,∠BDA=60°,知∠CDB=30°,
与向量综合
典例
例2.
与向量综合
练习
实际测量中的有关名称、术语
实际应用
测距
例3.
实际应用
测距
实际应用
练习
1.如图 ,一名学生在河岸紧靠岸边笔直行走,开始在A处,经观察,在河的对岸有一参照物C,与学生前进方向成30°角,学生前进200 m 后到达点B,测得该参照物与前进方向成75°角. (1)求点A与参照物C的距离;(2)求河的宽度.
实际应用
练习
2.如图,隔河看到两个目标A,B,但不能到达,在岸边选取相距 km的C,D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),求两个目标A,B之间的距离.
实际应用
测高
实际应用
练习
如图,为了测量河对岸的塔高AB,选取与塔底B在同一水平面内的两个测点C和D,测得CD=200 m,在点C和点D测得塔顶A的仰角分别是45°和30°,且∠CBD=30°,求塔高AB.
实际应用
测角
例6地图测绘人员在点A测得某一目标参照物P在他的北偏东30°的方向,且距离他40 m,之后该测绘人员沿正北方向行走了40 m,达到点B.试确定此时目标参照物P相对于他的方位角以及他与目标参照物P的距离.
因为AB=40 m,所以AB=PB,所以∠APB=∠PAB=30°,所以∠PBA=120°.因此测绘人员到达点B时,目标参照物P相对于该测绘人员的方位角为180°-120°=60°,且目标参照物P与他的距离为40 m.
实际应用
练习
如图所示,从A到B,方位角是50°,距离是470 m;从B到C,方位角是80°,距离是860 m;从C到D,方位角是150°,距离是640 m,试计算从A到D的方位角和距离.
实际应用
练习
如图所示,从A到B,方位角是50°,距离是470 m;从B到C,方位角是80°,距离是860 m;从C到D,方位角是150°,距离是640 m,试计算从A到D的方位角和距离.
2.6.1余弦定理、正弦定理
第三课时 用余弦定理、正弦定理解三角形
北师大(2019)必修2
聚焦知识目标和数学素养
1.了解三角函数是研究周期现象最重要的模型.(重点)
2.初步体会如何利用三角函数研究简单的实际问题.(难点)
1.会用正弦定理、余弦定理解决与三角形有关的几何计算问题.(数学运算、逻辑推理)
2.会用正弦定理、余弦定理解决与距离、高度、角度有关的实际问题.(数学建模、数学运算)
复习引入
在△ABC中,若角A,B,C所对的边分别是a,b,c,R为△ABC外接圆半径,则
1.正弦定理、余弦定理
定理 正弦定理 余弦定理
内容 = = =2R a2= ;
b2= ;
c2=_______________
b2+c2-2bccos A
c2+a2-2cacos B
a2+b2-2abcos C
变形 (1)a=2Rsin A,b= ,c= ; (2)sin A= ,sin B= ,sin C= ; (3)a∶b∶c= ; (4)asin B=bsin A, bsin C=csin B, asin C=csin A cos A= ;
cos B= ;
cos C=____________
2Rsin B
2Rsin C
sin A∶sin B∶sin C
2.在△ABC中,已知a、b和A时,解的情况如下:
A为锐角 A为钝角或直角
图形
关系式 a=bsin A bsin A
解的个数 一解 两解 一解 一解
3.三角形常用面积公式
(1)S= a·ha(ha表示边a上的高);
(2)S= absin C= = ;
(3)S= r(a+b+c)(r为三角形内切圆半径).
acsin B
bcsin A
1.三角形内角和定理
在△ABC中,A+B+C=π;
2.三角形中的三角函数关系
(1)sin(A+B)=sin C;(2)cos(A+B)=-cos C;
3.三角形中的射影定理
在△ABC中,a=bcos C+ccos B;b=acos C+ccos A;c=bcos A+acos B.
4.三角形常用结论
解三角形及相关应用
解三角形与三角形有关的几何计算
在三角形的三条边和三个角这6个元素中,如果已知3个(至少含一边长),那么由余弦定理和正弦定理,就可以求得其他3个元素.具体情形如下:
情形1 已知两个角的大小与一条边的边长.
先由三角形内角和等于180°求出第三个角的大小,然后依据正弦定理求得另外两条边的边长.
情形2 已知两条边的边长及其夹角的大小.
先由余弦定理求出第三条边的边长,然后再由余弦定理求得第二、第三个角的大小.
情形3 已知三条边的边长.
由余弦定理求出两个角,再利用三角形内角和等于180°求出第三个角.
情形4 已知两条边的边长和其中一边对角的大小.
首先,由正弦定理求出第二条边所对角的正弦,这时,要判断是两解、一解还是无解.然后,根据三角形内角和等于180°得到第三个角的大小.最后,由余弦定理或正弦定理求得第三条边的边长.
几何计算
典例
例1.
几何计算
练习
在四边形ABCD中,已知AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,求BC的长.
解在△ABD中,设BD=x,由余弦定理,得BA2=BD2+AD2-2BD·AD·cos∠BDA
即142=x2+102-2·10x·cos 60°,
整理得x2-10x-96=0,
解得x1=16,x2=-6(舍去),所以BD=16.
由AD⊥CD,∠BDA=60°,知∠CDB=30°,
与向量综合
典例
例2.
与向量综合
练习
实际测量中的有关名称、术语
实际应用
测距
例3.
实际应用
测距
实际应用
练习
1.如图 ,一名学生在河岸紧靠岸边笔直行走,开始在A处,经观察,在河的对岸有一参照物C,与学生前进方向成30°角,学生前进200 m 后到达点B,测得该参照物与前进方向成75°角. (1)求点A与参照物C的距离;(2)求河的宽度.
实际应用
练习
2.如图,隔河看到两个目标A,B,但不能到达,在岸边选取相距 km的C,D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),求两个目标A,B之间的距离.
实际应用
测高
实际应用
练习
如图,为了测量河对岸的塔高AB,选取与塔底B在同一水平面内的两个测点C和D,测得CD=200 m,在点C和点D测得塔顶A的仰角分别是45°和30°,且∠CBD=30°,求塔高AB.
实际应用
测角
例6地图测绘人员在点A测得某一目标参照物P在他的北偏东30°的方向,且距离他40 m,之后该测绘人员沿正北方向行走了40 m,达到点B.试确定此时目标参照物P相对于他的方位角以及他与目标参照物P的距离.
因为AB=40 m,所以AB=PB,所以∠APB=∠PAB=30°,所以∠PBA=120°.因此测绘人员到达点B时,目标参照物P相对于该测绘人员的方位角为180°-120°=60°,且目标参照物P与他的距离为40 m.
实际应用
练习
如图所示,从A到B,方位角是50°,距离是470 m;从B到C,方位角是80°,距离是860 m;从C到D,方位角是150°,距离是640 m,试计算从A到D的方位角和距离.
实际应用
练习
如图所示,从A到B,方位角是50°,距离是470 m;从B到C,方位角是80°,距离是860 m;从C到D,方位角是150°,距离是640 m,试计算从A到D的方位角和距离.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
