2021-2022年初中数学八年级下册17.1勾股定理课堂练习(Word版含答案)
文档属性
| 名称 | 2021-2022年初中数学八年级下册17.1勾股定理课堂练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 409.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 20:30:58 | ||
图片预览



文档简介
2021-2022年初中数学八年级下册同步(人教版)
17.1勾股定理-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知一个的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
2.如果3,a,5是勾股数,则a的值是( )
A.4 B. C.4或 D.4或34
3.如图所示,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A'点,连接A'B,则线段A'B与线段AC的关系是 ( )
A.垂直 B.相等 C.平分 D.平分且垂直
4.在中,,,则( ).
A.100 B.200 C.300 D.400
5.如图所示,用四个全等的直角三角形和一个小正方形拼成一个大正方形已知大正方形的面积为49,小正方形的面积为4.用,表示直角三角形的两直角边(),请仔细观察图案.下列关系式中不正确的是( )
A. B.
C. D.
6.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度hcm,则h的取值范围是( )
A.h≤17cm B.h≥8cm
C.15cm≤h≤16cm D.7cm≤h≤16cm
二、填空题
7.如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5米,顶点A在AC上滑动,量得滑竿下端B距C点的距离为1.5米,当端点B向右移动0.5米时,滑竿顶端A下滑________米.
8.有两棵树,一棵高米,另一棵高米,两树相距米,一只鸟从一棵树的树梢飞到另一个树的树梢,则小鸟至少飞行_________________米
9.有—个长为12cm,宽为,高为3cm的长方形铁盒,在其内部要放一根笔直的铅笔,则铅笔长度不应超过_______.
10.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了520m,则该河流的宽度为_______m.
11.《中华人民共和国道路交通管理条例》规定,小汽车在城市街道上的行驶速度不得超过70km/h.如图所示,一辆小汽车在一条城市街道沿直道向处行驶.某一时刻刚好行驶到路对面车速检测仪正前方30m处的点,过了2s后,测得小汽车与车速检测仪之间的距离为50m,这辆小汽车________.(填“超速”或“不超速”)
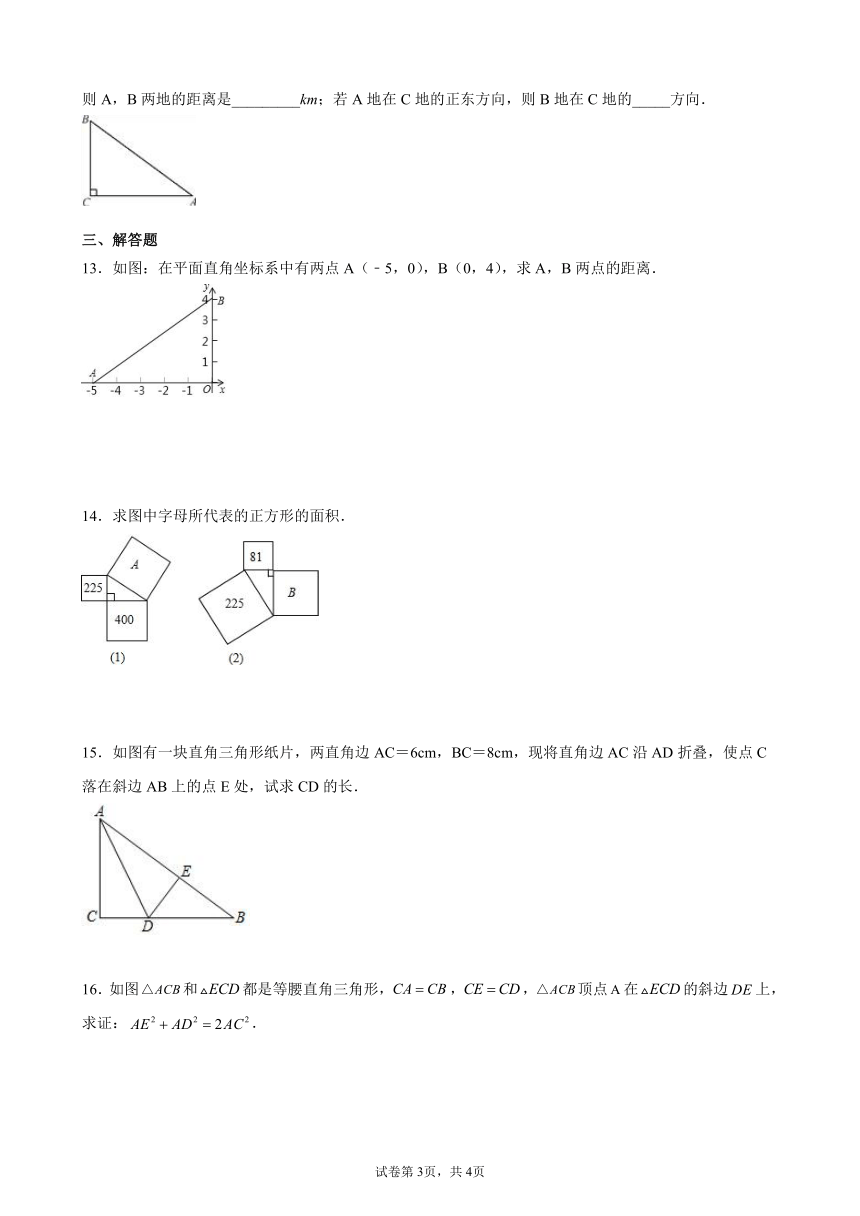
12.已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4 km,B,C两地的距离是3 km,则A,B两地的距离是_________km;若A地在C地的正东方向,则B地在C地的_____方向.
三、解答题
13.如图:在平面直角坐标系中有两点A(﹣5,0),B(0,4),求A,B两点的距离.
14.求图中字母所代表的正方形的面积.
15.如图有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿AD折叠,使点C落在斜边AB上的点E处,试求CD的长.
16.如图和都是等腰直角三角形,,,顶点在的斜边上,求证:.
17.如图,,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,隧道总长为2公里,已知高速公路一公里造价为300万元,隧道一公里造价为500万元,公里,公里,则改建后可省工程费用多少万元?
18.如图,已知.
(1)说出数轴上点所表示的数;
(2)比较点所表示的数与的大小.
试卷第4页,共4页
试卷第3页,共4页
参考答案
1.D
【解析】解:由于4是三角形的直角边与斜边不能确定,故应分两种情况进行讨论:
(1)3、4都为直角边,由勾股定理得,斜边为5;
(2)3为直角边,4为斜边,由勾股定理得,直角边为.
∴第三边长的平方是25或7,
故选:D.
2.A
【解析】解:∵3,a,5是勾股数,∴或
∴a=(舍去 )或a=4
故选A.
3.D
【解析】解:如图,将点A先向下平移3格,再向左平移1格到达A′点,连接A′B,与线段AC交于点O.
∵A′O=OB=,AO=OC=2,
∴线段A′B与线段AC互相平分,
又∵∠AOA′=45°+45°=90°,
∴A′B⊥AC,
∴线段A′B与线段AC互相垂直平分.
故选D.
4.C
【解析】解:∵在中,且,
∴AB为的斜边,
∴根据勾股定理得:,
∴,
故选:C.
5.D
【解析】A中,根据勾股定理等于大正方形边长的平方,它就是正方形的面积,故正确;
B中,根据小正方形的边长是2它等于三角形较长的直角边减较短的直角边即可得到,正确;
C中,根据四个直角三角形的面积和加上小正方形的面积即可得到,正确;
D中,根据A可得,C可得,结合完全平方公式可以求得,错误.
故选D.
6.D
【解析】解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,
∴h=24﹣8=16cm;
当筷子的底端在A点时,筷子露在杯子外面的长度最短,
在Rt△ABD中,AD=15,BD=8,
∴AB==17,
∴此时h=24﹣17=7cm,
所以h的取值范围是7cm≤h≤16cm.
故选:D.
7.0.5
【解析】结合题意可知AB=DE=2.5米,BC=1.5米,BD=0.5米,∠C=90°,
∴AC===2(米).
∵BD=0.5米,
∴CD=2米,
∴CE===1.5(米),
∴AE=AC-EC=0.5(米).
故答案为0.5.
8.
【解析】解:如图,设大树高为,
小树高为,
过点作于,则四边形是矩形,
连接,
,,,
在中,
.
故小鸟至少飞行.
故答案为:10.
9.13
【解析】由题意知:AD=12cm,CD=4cm,BC=3cm
∵, ,
∴,
∴AB=13(cm),(负值舍去),
答:铅笔长度不应超过13cm.
故答案为:13.
10.480
【解析】解析: 根据题意,
故答案为480.
11.超速
【解析】在中,,所以.
因此,小汽车的速度为.,故这辆小汽车超速.
12.5 正北
【解析】∵∠C=90°,A,C两地的距离是4km,B,C两地的距离是3km,∴AB===5(km),又∵A地在C地的正东方向,则B地在C地的 正北方向.故答案为5;正北.
13.
【解析】解:AO=5,BO=4,
由勾股定理得:.
14.A所代表的正方形的面积是625,B所代表的正方形的面积是144
【解析】解:A的边长为直角三角形的斜边,则A的边长的平方等于两直角边边长的平方和,两条直角边的平方分别为:225和400,
A的面积=225+400=625,
同理B的边长为直角三角形的直角边,则存在B的边长的平方等于斜边的平方减去另一直角边的平方,斜边的平方为225,直角边的平方为81
B的面积为225﹣81=144.
15.3cm
【解析】解:是直角三角形,AC=6cm,BC=8cm,
∴,
∵是翻折而成,
∴,DE=CD,∠AED=∠C=90°,
∴,
在中,,设DE=CD=xcm,则BD=8-x,
即,
解得:,
故CD的长为3cm.
16.证明见解析.
【解析】证明:如图,连结BD ,
∵,
∴.
∴在△EAC和△DBC中,,
∴.
∴ .
又∵,
∴ .
∴ 在中,,
∴.
∵ 在中,,
∴ .
17.11600
【解析】解:根据勾股定理得:
原计划建公路费用:万元,
实际打隧道及建公路费用:万元,
万元,
答:改建后可省工程费11600万元.
18.(1)点表示;(2)
【解析】解:(1),
即数轴上点所表示的数是;
(2),
,
即比较点所表示的数大于.答案第6页,共1页
答案第5页,共5页
17.1勾股定理-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知一个的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
2.如果3,a,5是勾股数,则a的值是( )
A.4 B. C.4或 D.4或34
3.如图所示,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A'点,连接A'B,则线段A'B与线段AC的关系是 ( )
A.垂直 B.相等 C.平分 D.平分且垂直
4.在中,,,则( ).
A.100 B.200 C.300 D.400
5.如图所示,用四个全等的直角三角形和一个小正方形拼成一个大正方形已知大正方形的面积为49,小正方形的面积为4.用,表示直角三角形的两直角边(),请仔细观察图案.下列关系式中不正确的是( )
A. B.
C. D.
6.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度hcm,则h的取值范围是( )
A.h≤17cm B.h≥8cm
C.15cm≤h≤16cm D.7cm≤h≤16cm
二、填空题
7.如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5米,顶点A在AC上滑动,量得滑竿下端B距C点的距离为1.5米,当端点B向右移动0.5米时,滑竿顶端A下滑________米.
8.有两棵树,一棵高米,另一棵高米,两树相距米,一只鸟从一棵树的树梢飞到另一个树的树梢,则小鸟至少飞行_________________米
9.有—个长为12cm,宽为,高为3cm的长方形铁盒,在其内部要放一根笔直的铅笔,则铅笔长度不应超过_______.
10.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了520m,则该河流的宽度为_______m.
11.《中华人民共和国道路交通管理条例》规定,小汽车在城市街道上的行驶速度不得超过70km/h.如图所示,一辆小汽车在一条城市街道沿直道向处行驶.某一时刻刚好行驶到路对面车速检测仪正前方30m处的点,过了2s后,测得小汽车与车速检测仪之间的距离为50m,这辆小汽车________.(填“超速”或“不超速”)
12.已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4 km,B,C两地的距离是3 km,则A,B两地的距离是_________km;若A地在C地的正东方向,则B地在C地的_____方向.
三、解答题
13.如图:在平面直角坐标系中有两点A(﹣5,0),B(0,4),求A,B两点的距离.
14.求图中字母所代表的正方形的面积.
15.如图有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿AD折叠,使点C落在斜边AB上的点E处,试求CD的长.
16.如图和都是等腰直角三角形,,,顶点在的斜边上,求证:.
17.如图,,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,隧道总长为2公里,已知高速公路一公里造价为300万元,隧道一公里造价为500万元,公里,公里,则改建后可省工程费用多少万元?
18.如图,已知.
(1)说出数轴上点所表示的数;
(2)比较点所表示的数与的大小.
试卷第4页,共4页
试卷第3页,共4页
参考答案
1.D
【解析】解:由于4是三角形的直角边与斜边不能确定,故应分两种情况进行讨论:
(1)3、4都为直角边,由勾股定理得,斜边为5;
(2)3为直角边,4为斜边,由勾股定理得,直角边为.
∴第三边长的平方是25或7,
故选:D.
2.A
【解析】解:∵3,a,5是勾股数,∴或
∴a=(舍去 )或a=4
故选A.
3.D
【解析】解:如图,将点A先向下平移3格,再向左平移1格到达A′点,连接A′B,与线段AC交于点O.
∵A′O=OB=,AO=OC=2,
∴线段A′B与线段AC互相平分,
又∵∠AOA′=45°+45°=90°,
∴A′B⊥AC,
∴线段A′B与线段AC互相垂直平分.
故选D.
4.C
【解析】解:∵在中,且,
∴AB为的斜边,
∴根据勾股定理得:,
∴,
故选:C.
5.D
【解析】A中,根据勾股定理等于大正方形边长的平方,它就是正方形的面积,故正确;
B中,根据小正方形的边长是2它等于三角形较长的直角边减较短的直角边即可得到,正确;
C中,根据四个直角三角形的面积和加上小正方形的面积即可得到,正确;
D中,根据A可得,C可得,结合完全平方公式可以求得,错误.
故选D.
6.D
【解析】解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,
∴h=24﹣8=16cm;
当筷子的底端在A点时,筷子露在杯子外面的长度最短,
在Rt△ABD中,AD=15,BD=8,
∴AB==17,
∴此时h=24﹣17=7cm,
所以h的取值范围是7cm≤h≤16cm.
故选:D.
7.0.5
【解析】结合题意可知AB=DE=2.5米,BC=1.5米,BD=0.5米,∠C=90°,
∴AC===2(米).
∵BD=0.5米,
∴CD=2米,
∴CE===1.5(米),
∴AE=AC-EC=0.5(米).
故答案为0.5.
8.
【解析】解:如图,设大树高为,
小树高为,
过点作于,则四边形是矩形,
连接,
,,,
在中,
.
故小鸟至少飞行.
故答案为:10.
9.13
【解析】由题意知:AD=12cm,CD=4cm,BC=3cm
∵, ,
∴,
∴AB=13(cm),(负值舍去),
答:铅笔长度不应超过13cm.
故答案为:13.
10.480
【解析】解析: 根据题意,
故答案为480.
11.超速
【解析】在中,,所以.
因此,小汽车的速度为.,故这辆小汽车超速.
12.5 正北
【解析】∵∠C=90°,A,C两地的距离是4km,B,C两地的距离是3km,∴AB===5(km),又∵A地在C地的正东方向,则B地在C地的 正北方向.故答案为5;正北.
13.
【解析】解:AO=5,BO=4,
由勾股定理得:.
14.A所代表的正方形的面积是625,B所代表的正方形的面积是144
【解析】解:A的边长为直角三角形的斜边,则A的边长的平方等于两直角边边长的平方和,两条直角边的平方分别为:225和400,
A的面积=225+400=625,
同理B的边长为直角三角形的直角边,则存在B的边长的平方等于斜边的平方减去另一直角边的平方,斜边的平方为225,直角边的平方为81
B的面积为225﹣81=144.
15.3cm
【解析】解:是直角三角形,AC=6cm,BC=8cm,
∴,
∵是翻折而成,
∴,DE=CD,∠AED=∠C=90°,
∴,
在中,,设DE=CD=xcm,则BD=8-x,
即,
解得:,
故CD的长为3cm.
16.证明见解析.
【解析】证明:如图,连结BD ,
∵,
∴.
∴在△EAC和△DBC中,,
∴.
∴ .
又∵,
∴ .
∴ 在中,,
∴.
∵ 在中,,
∴ .
17.11600
【解析】解:根据勾股定理得:
原计划建公路费用:万元,
实际打隧道及建公路费用:万元,
万元,
答:改建后可省工程费11600万元.
18.(1)点表示;(2)
【解析】解:(1),
即数轴上点所表示的数是;
(2),
,
即比较点所表示的数大于.答案第6页,共1页
答案第5页,共5页
