2021-2022年初中数学八年级下册18.1.1平行四边形的性质课堂练习(Word版含答案)
文档属性
| 名称 | 2021-2022年初中数学八年级下册18.1.1平行四边形的性质课堂练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 320.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 00:00:00 | ||
图片预览




文档简介
2021-2022年初中数学八年级下册同步(人教版)
18.1.1平行四边形的性质-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.平行四边形的一边长为10,那么它的两条对角线的长可以是( )
A.4和6 B.6和8 C.8和12 D.20和30
2.如图,在中,已知,,,则的长为( )
A. B. C. D.
3.平行四边形的一组对角的平分线( )
A.一定相互平行 B.一定相交 C.可能平行也可能相交 D.平行或共线
4.如图,平行四边形ABCD的对角线AC与BD相交于点O,AE⊥BC于E,AB=,AC=2,BD=4,则AE的长为( )
A. B. C. D.
5.平行四边形的两条对角线长分别是、,一边长为12,则、可能是下列各组中的( )
A.8与14 B.10与14 C.18与20 D.10与38
6.平行四边形的边长为5,则它的对角线长可能是( )
A.4和6 B.2和12 C.4和8 D.4和3
二、填空题
7.从平行四边形的一个锐角顶点作两条高线,如果这两条高线夹角为,则这个平行四边形的各内角的度数为_________.
8.在中,,在上取,则的度数是_______.
9.如图,在中,交于O,若,则的长为_________.
10.过对角线交点O作直线m,分别交直线于点E,交直线于点F,若,则的长是_________.
11.如图所示,将四根木条组成的矩形木框变成 ABCD的形状,并使其面积变为原来的一半,则这个平行四边形的一个最小的内角的度数是_____.
12.已知平行四边形的面积为144,相邻两边上的高分别为8和9,则它的周长为_____.
三、解答题
13.如图,A,B两点被大山阻隔,为了改善山区的交通,现拟开凿一个贯穿A,B的隧道,修建一条高速公路.请你设计出一个方案,利用平移的有关知识测量出A,B之间的距离和隧道开凿的方向.
14.如图,在中,对角线与相交于点O,.求的长度及的面积.
15.如图,小斌用一根50m长的绳子围成一个平行四边形场地,其中一边长16m,求其他三边的长度.
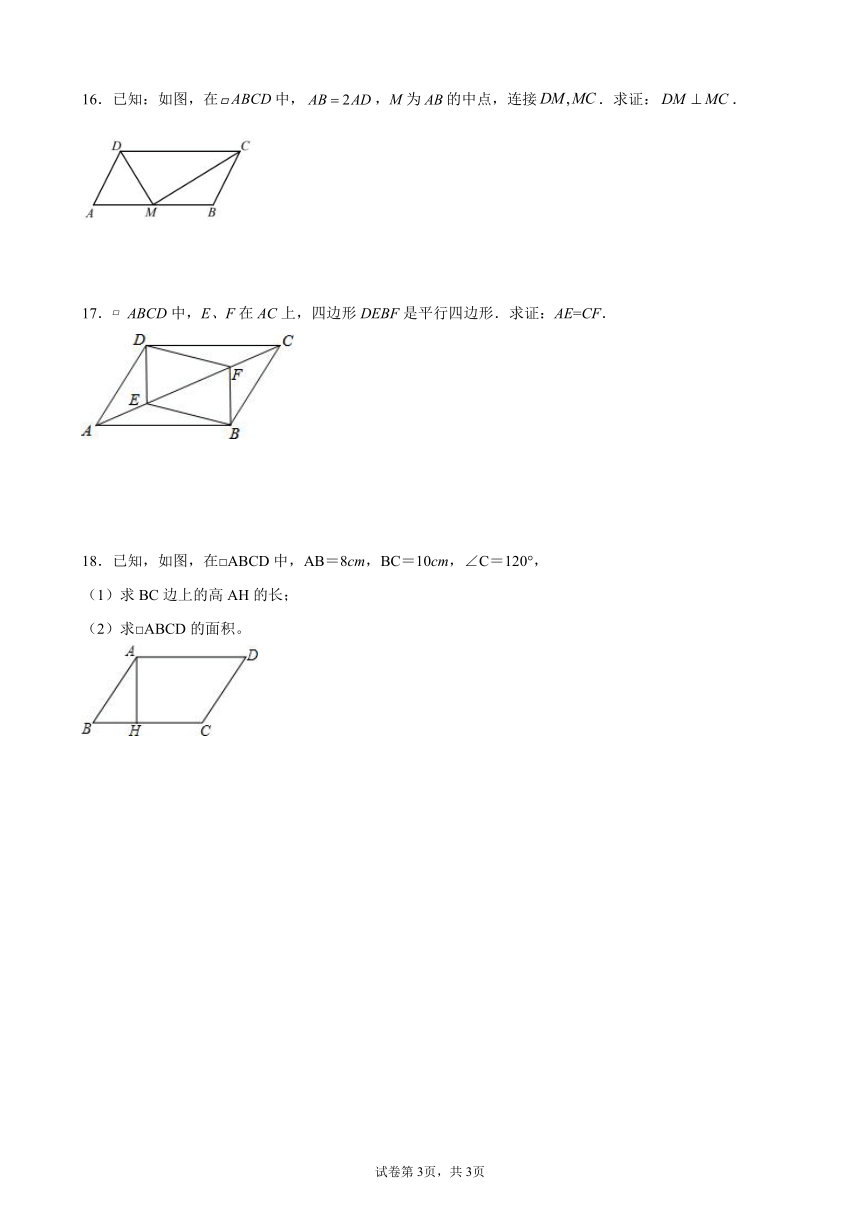
16.已知:如图,在中,,M为的中点,连接.求证:.
17. ABCD中,E、F在AC上,四边形DEBF是平行四边形.求证:AE=CF.
18.已知,如图,在□ABCD中,AB=8cm,BC=10cm,∠C=120°,
(1)求BC边上的高AH的长;
(2)求□ABCD的面积。
试卷第2页,共3页
试卷第3页,共3页
参考答案
1.D
【解析】解:如图,设AB=10,对角线相交于点E,
它的两条对角线的长为4和6时,,不符合题意;
它的两条对角线的长为6和8时,,不符合题意;
它的两条对角线的长为8和12时,,不符合题意;
它的两条对角线的长为20和30时,设AE=15,BE=10,,符合题意;
故选:D.
2.A
【解析】解:四边形是平行四边形,,
,,
,
.
故选:A.
3.D
【解析】解:如图,中,AE、CF分别平分∠BAD、∠BCD,
∵四边形ABCD是平行四边形,AD∥BC,
∴∠BAD=∠BCD,∠2=∠3,
∵AE、CF分别平分∠BAD、∠BCD,
∴,
∴∠2=∠4,
∴∠3=∠4,
∴AE∥CF;
当是菱形时,AE与CF共线.
故选:D.
4.D
【解析】解:∵AC=2,BD=4,四边形ABCD是平行四边形,
∴AO=AC=1,BO=BD=2,
∵AB=,
∴AB2+AO2=BO2,
∴∠BAC=90°,
∵在Rt△BAC中,BC=,S△BAC=×AB×AC=×BC×AE,
∴×2=AE,
∴AE=,
故选:D.
5.C
【解析】解:∵平行四边形的对角线互相平分,此平行四边形的两对角线长为
∴这两条对角线的一半就是,
∴这两条对角线的一半与边长为12的边组成的三角形的三边为:、、12
根据三角形任意两边之和大于第三边得:
A选项中,不符合;B选项中,不符合;C选项中,符合;D选项中,不符合.
故选:C
6.C
【解析】A. 对角线一半分别是2和3,2+3=5,不能构成三角形,故本选项错误;
B. 对角线一半分别是1和6,6 1=5,不能构成三角形,故本选项错误.
C. 对角线一半分别是2和4,符合三角形的三边关系,能构成三角形,故本选项正确;
D. 对角线一半分别是2和,2+<5,不能构成三角形,故本选项错误.
故选C.
7.
【解析】解:根据题意画出图形,如下图,
根据题意得: , ,
在四边形AECF中,
,
∴ ,
在平行四边形ABCD中, , , ,
∴,,
∴这个平行四边形的各内角的度数为.
故答案为:.
8.
【解析】
解:在平行四边形ABCD中,∠A=130°,
∴∠BCD=∠A=130°,∠D=180° 130°=50°,
∵DE=DC,
∴,
∴∠ECB=130° 65°=65°.
故答案为:65°.
9.36
【解析】解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,
∵OA=3x,AC=5x+12,
∴3x=(5x+12),
解得:x=12,
∴OC=3x=36.
故答案为:36.
10.10或2
【解析】当F在DC的反向延长线上时,如图1所示,
四边形ABCD是平行四边形,
在和中,
当F在DC的延长线上时,如图2所示,
BE = 4 + 6= 10,
DF = 10.
故答案为:10或2.
11.30°
【解析】解:过A作AE⊥BC于点E,如图所示:
由四根木条组成的矩形木框变成 ABCD的形状,面积变为原来的一半,
得到AE=AB,又△ABE为直角三角形,
∴∠ABE=30°,
则平行四边形中最小的内角为30°.
故答案为30°
12.68
【解析】由平行四边形的面积是144,相邻两边上的高分别为8和9,即可根据平行四边形的面积公式求得其相邻两边的长144÷8=18,144÷9=16,因此可得它的周长是:18+16+18+16=68.
故答案为68.
13.见解析
【解析】解:可以设法将线段“平移”出来,便于测量.如图,分别沿A,B两点向同一个方向行走相同距离得到点,测量线段即可,这是其中一种方法.
14.OB的长为3, ABCD的面积为48.
【解析】解:∵BD⊥AD,AB=10,AD=8,
∴BD==6.
∵四边形ABCD是平行四边形,
∴OB=BD=3,
∴S ABCD=6×8=48.
故OB的长为3, ABCD的面积为48.
15.其他三边的长为9m,16m,9m.
【解析】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵周长为50,
∴AB+BC=25,
∵一边长为16m,
∴另一边长为9m,
∴其他三边的长为9m,16m,9m.
16.见解析
【解析】证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,
∴∠CDM=∠AMD,∠DCM=∠BMC,
∵AB=2AD,M为AB的中点,
∴AD=AM=BM=BC,
∴∠ADM=∠AMD,∠BCM=∠BMC,
∴∠ADM=∠CDM=∠ADC,∠DCM=∠BCM=∠BCD,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠CDM+∠DCM=90°,
∴∠DMC=90°,
即DM⊥MC.
17.见解析
【解析】证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,四边形DEBF是平行四边形,
∴OA=OC,OE=OF,
∴OA-OE=OC-OF,
∴AE=CF.
18.(1)4 (2)40
【解析】(1)∵在□ABCD中,AB∥CD,∴∠B=180°-120°=60°
在直角三角形ABH中,AH=AB sin=8×=。
(2)S平行四边形ABCD=BC AH=。
答案第6页,共6页
答案第7页,共1页
18.1.1平行四边形的性质-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.平行四边形的一边长为10,那么它的两条对角线的长可以是( )
A.4和6 B.6和8 C.8和12 D.20和30
2.如图,在中,已知,,,则的长为( )
A. B. C. D.
3.平行四边形的一组对角的平分线( )
A.一定相互平行 B.一定相交 C.可能平行也可能相交 D.平行或共线
4.如图,平行四边形ABCD的对角线AC与BD相交于点O,AE⊥BC于E,AB=,AC=2,BD=4,则AE的长为( )
A. B. C. D.
5.平行四边形的两条对角线长分别是、,一边长为12,则、可能是下列各组中的( )
A.8与14 B.10与14 C.18与20 D.10与38
6.平行四边形的边长为5,则它的对角线长可能是( )
A.4和6 B.2和12 C.4和8 D.4和3
二、填空题
7.从平行四边形的一个锐角顶点作两条高线,如果这两条高线夹角为,则这个平行四边形的各内角的度数为_________.
8.在中,,在上取,则的度数是_______.
9.如图,在中,交于O,若,则的长为_________.
10.过对角线交点O作直线m,分别交直线于点E,交直线于点F,若,则的长是_________.
11.如图所示,将四根木条组成的矩形木框变成 ABCD的形状,并使其面积变为原来的一半,则这个平行四边形的一个最小的内角的度数是_____.
12.已知平行四边形的面积为144,相邻两边上的高分别为8和9,则它的周长为_____.
三、解答题
13.如图,A,B两点被大山阻隔,为了改善山区的交通,现拟开凿一个贯穿A,B的隧道,修建一条高速公路.请你设计出一个方案,利用平移的有关知识测量出A,B之间的距离和隧道开凿的方向.
14.如图,在中,对角线与相交于点O,.求的长度及的面积.
15.如图,小斌用一根50m长的绳子围成一个平行四边形场地,其中一边长16m,求其他三边的长度.
16.已知:如图,在中,,M为的中点,连接.求证:.
17. ABCD中,E、F在AC上,四边形DEBF是平行四边形.求证:AE=CF.
18.已知,如图,在□ABCD中,AB=8cm,BC=10cm,∠C=120°,
(1)求BC边上的高AH的长;
(2)求□ABCD的面积。
试卷第2页,共3页
试卷第3页,共3页
参考答案
1.D
【解析】解:如图,设AB=10,对角线相交于点E,
它的两条对角线的长为4和6时,,不符合题意;
它的两条对角线的长为6和8时,,不符合题意;
它的两条对角线的长为8和12时,,不符合题意;
它的两条对角线的长为20和30时,设AE=15,BE=10,,符合题意;
故选:D.
2.A
【解析】解:四边形是平行四边形,,
,,
,
.
故选:A.
3.D
【解析】解:如图,中,AE、CF分别平分∠BAD、∠BCD,
∵四边形ABCD是平行四边形,AD∥BC,
∴∠BAD=∠BCD,∠2=∠3,
∵AE、CF分别平分∠BAD、∠BCD,
∴,
∴∠2=∠4,
∴∠3=∠4,
∴AE∥CF;
当是菱形时,AE与CF共线.
故选:D.
4.D
【解析】解:∵AC=2,BD=4,四边形ABCD是平行四边形,
∴AO=AC=1,BO=BD=2,
∵AB=,
∴AB2+AO2=BO2,
∴∠BAC=90°,
∵在Rt△BAC中,BC=,S△BAC=×AB×AC=×BC×AE,
∴×2=AE,
∴AE=,
故选:D.
5.C
【解析】解:∵平行四边形的对角线互相平分,此平行四边形的两对角线长为
∴这两条对角线的一半就是,
∴这两条对角线的一半与边长为12的边组成的三角形的三边为:、、12
根据三角形任意两边之和大于第三边得:
A选项中,不符合;B选项中,不符合;C选项中,符合;D选项中,不符合.
故选:C
6.C
【解析】A. 对角线一半分别是2和3,2+3=5,不能构成三角形,故本选项错误;
B. 对角线一半分别是1和6,6 1=5,不能构成三角形,故本选项错误.
C. 对角线一半分别是2和4,符合三角形的三边关系,能构成三角形,故本选项正确;
D. 对角线一半分别是2和,2+<5,不能构成三角形,故本选项错误.
故选C.
7.
【解析】解:根据题意画出图形,如下图,
根据题意得: , ,
在四边形AECF中,
,
∴ ,
在平行四边形ABCD中, , , ,
∴,,
∴这个平行四边形的各内角的度数为.
故答案为:.
8.
【解析】
解:在平行四边形ABCD中,∠A=130°,
∴∠BCD=∠A=130°,∠D=180° 130°=50°,
∵DE=DC,
∴,
∴∠ECB=130° 65°=65°.
故答案为:65°.
9.36
【解析】解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,
∵OA=3x,AC=5x+12,
∴3x=(5x+12),
解得:x=12,
∴OC=3x=36.
故答案为:36.
10.10或2
【解析】当F在DC的反向延长线上时,如图1所示,
四边形ABCD是平行四边形,
在和中,
当F在DC的延长线上时,如图2所示,
BE = 4 + 6= 10,
DF = 10.
故答案为:10或2.
11.30°
【解析】解:过A作AE⊥BC于点E,如图所示:
由四根木条组成的矩形木框变成 ABCD的形状,面积变为原来的一半,
得到AE=AB,又△ABE为直角三角形,
∴∠ABE=30°,
则平行四边形中最小的内角为30°.
故答案为30°
12.68
【解析】由平行四边形的面积是144,相邻两边上的高分别为8和9,即可根据平行四边形的面积公式求得其相邻两边的长144÷8=18,144÷9=16,因此可得它的周长是:18+16+18+16=68.
故答案为68.
13.见解析
【解析】解:可以设法将线段“平移”出来,便于测量.如图,分别沿A,B两点向同一个方向行走相同距离得到点,测量线段即可,这是其中一种方法.
14.OB的长为3, ABCD的面积为48.
【解析】解:∵BD⊥AD,AB=10,AD=8,
∴BD==6.
∵四边形ABCD是平行四边形,
∴OB=BD=3,
∴S ABCD=6×8=48.
故OB的长为3, ABCD的面积为48.
15.其他三边的长为9m,16m,9m.
【解析】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵周长为50,
∴AB+BC=25,
∵一边长为16m,
∴另一边长为9m,
∴其他三边的长为9m,16m,9m.
16.见解析
【解析】证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,
∴∠CDM=∠AMD,∠DCM=∠BMC,
∵AB=2AD,M为AB的中点,
∴AD=AM=BM=BC,
∴∠ADM=∠AMD,∠BCM=∠BMC,
∴∠ADM=∠CDM=∠ADC,∠DCM=∠BCM=∠BCD,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠CDM+∠DCM=90°,
∴∠DMC=90°,
即DM⊥MC.
17.见解析
【解析】证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,四边形DEBF是平行四边形,
∴OA=OC,OE=OF,
∴OA-OE=OC-OF,
∴AE=CF.
18.(1)4 (2)40
【解析】(1)∵在□ABCD中,AB∥CD,∴∠B=180°-120°=60°
在直角三角形ABH中,AH=AB sin=8×=。
(2)S平行四边形ABCD=BC AH=。
答案第6页,共6页
答案第7页,共1页
