吉林省长白山一高2013学年高一数学必修1综合检测题 第3章
文档属性
| 名称 | 吉林省长白山一高2013学年高一数学必修1综合检测题 第3章 |

|
|
| 格式 | zip | ||
| 文件大小 | 69.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-22 21:47:11 | ||
图片预览


文档简介
第三章综合素能检测
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分。考试时间120分钟。
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.给出下列四个命题:①函数f(x)=3x-6的零点是2;②函数f(x)=x2+4x+4的零点是-2;③函数f(x)=log3(x-1)的零点是1;④函数f(x)=2x-1的零点是0.其中正确的个数为( )
A.1 B.2 C.3 D.4
2.若函数y=f(x)在区间[0,4]上的图象是连续不断的曲线,且方程f(x)=0在(0,4)内仅有一个实数根,则f(0)·f(4)的值( )
A.大于0 B.小于0
C.等于0 D.无法判断
3.函数f(x)=ax+b的零点是-1(a≠0),则函数g(x)=ax2+bx的零点是( )
A.-1 B.0
C.-1和0 D.1和0
4.方程lgx+x-2=0一定有解的区间是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
5.某商场对顾客实行购物优惠活动,规定一次购物付款总额,
①如果不超过200元,则不予优惠.
②如果超过200元,但不超过500元,则按标准价给予9折优惠.
③如果超过500元,则其500元按第②条给予优惠,超过500元的部分给予7折优惠.
某人两次去购物,分别付款168元和423元,假设他只去一次购买上述同样的商品,则应付款是( )
A.413.7元 B.513.6元
C.546.6元 D.548.7元
6.设函数f(x)=,则方程f(x)=的解为( )
A. B.3
C.3或 D.无解
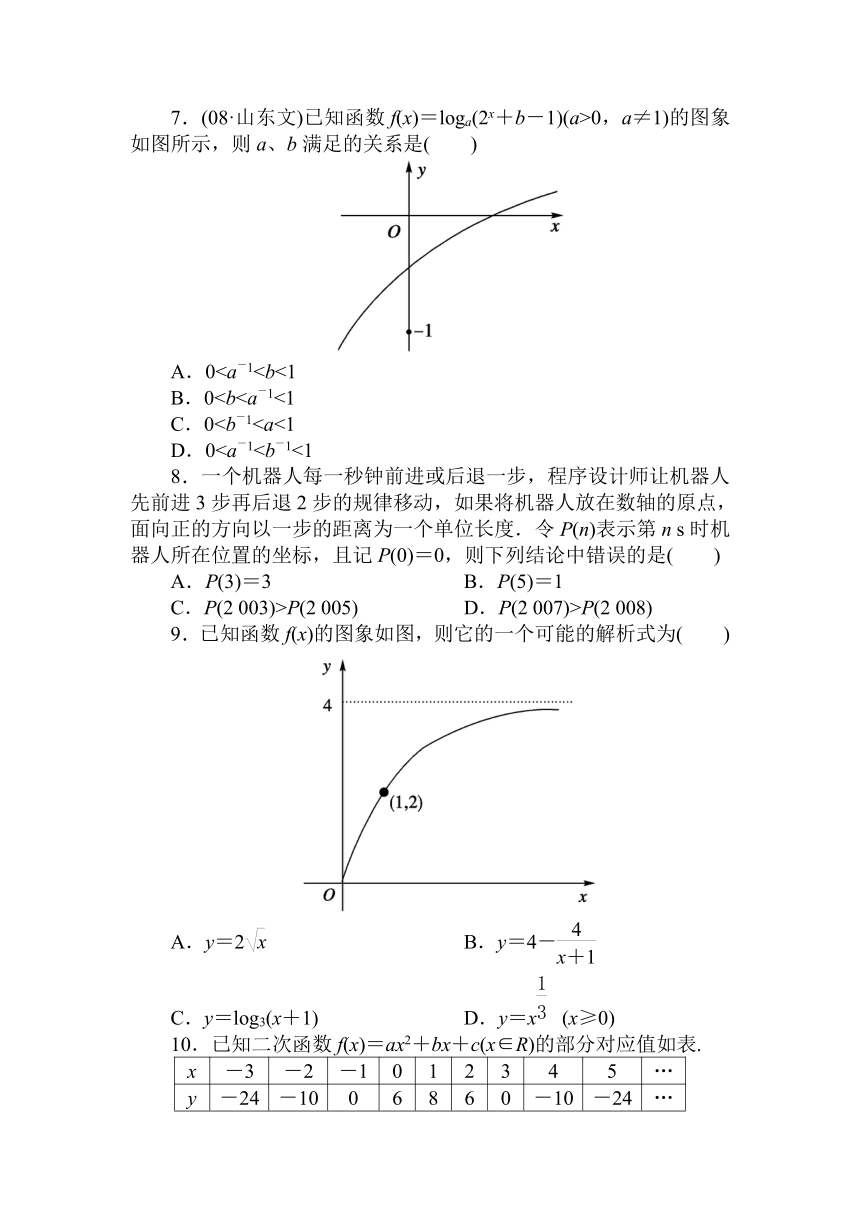
7.(08·山东文)已知函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a、b满足的关系是( )
A.0B.0C.0D.08.一个机器人每一秒钟前进或后退一步,程序设计师让机器人先前进3步再后退2步的规律移动,如果将机器人放在数轴的原点,面向正的方向以一步的距离为一个单位长度.令P(n)表示第n s时机器人所在位置的坐标,且记P(0)=0,则下列结论中错误的是( )
A.P(3)=3 B.P(5)=1
C.P(2 003)>P(2 005) D.P(2 007)>P(2 008)
9.已知函数f(x)的图象如图,则它的一个可能的解析式为( )
A.y=2 B.y=4-
C.y=log3(x+1) D.y=x (x≥0)
10.已知二次函数f(x)=ax2+bx+c(x∈R)的部分对应值如表.
x
-3
-2
-1
0
1
2
3
4
5
…
y
-24
-10
0
6
8
6
0
-10
-24
…
则使ax2+bx+c>0成立的x的取值范围是( )
A.(-10,-1)∪(1+∞)
B.(-∞,-1)∪(3+∞)
C.(-1,3)
D.(0,+∞)
11.方程4x-3×2x+2=0的根的个数是( )
A.0 B.1 C.2 D.3
12.若方程mx-x-m=0(m>0,且m≠1)有两个不同实数根,则m的取值范围是( )
A.m>1 B.0<m<1
C.m>0 D.m>2
第
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
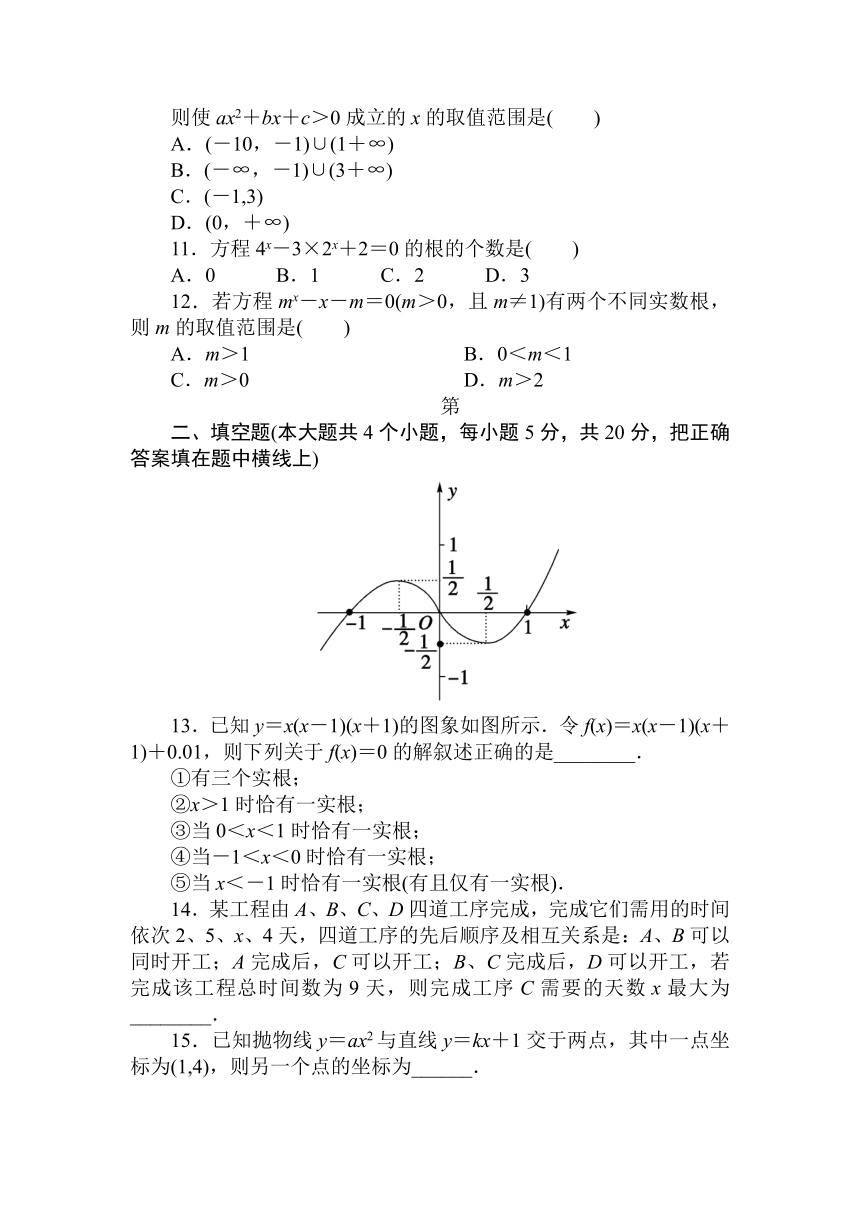
13.已知y=x(x-1)(x+1)的图象如图所示.令f(x)=x(x-1)(x+1)+0.01,则下列关于f(x)=0的解叙述正确的是________.
①有三个实根;
②x>1时恰有一实根;
③当0<x<1时恰有一实根;
④当-1<x<0时恰有一实根;
⑤当x<-1时恰有一实根(有且仅有一实根).
14.某工程由A、B、C、D四道工序完成,完成它们需用的时间依次2、5、x、4天,四道工序的先后顺序及相互关系是:A、B可以同时开工;A完成后,C可以开工;B、C完成后,D可以开工,若完成该工程总时间数为9天,则完成工序C需要的天数x最大为________.
15.已知抛物线y=ax2与直线y=kx+1交于两点,其中一点坐标为(1,4),则另一个点的坐标为______.
16.已知函数f(x)=,则方程f(x)=的解为________.
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本题满分10分)方程x2-=0在(-∞,0)内是否存在实数解?并说明理由.
18.(本题满分12分)北京市的一家报刊摊点,从报社买进《北京日报》的价格是每份0.20元,卖出的价格是每份0.30元,卖不掉的报纸可以以每份0.05元的价格退回报社.在一个月(30天计算)里,有20天每天可卖出400份,其余10天每天只能卖出250份,但每天从报社买进的份数必须相同,这个摊主每天从报社买进多少份,才能使每月所获的利润最大?并计算他一个月最多可赚得多少元?
19.(本题满分12分)若关于x的方程x2-2ax+2+a=0有两个不相等的实根,求分别满足下列条件的a的取值范围.
(1)方程两根都大于1;
(2)方程一根大于1,另一根小于1.
20.(本题满分12分)某化工厂生产的一种溶液,按市场要求,杂质含量不能超过0.1%.若初时含杂质2%,每过滤一次可使杂质含量减少,问至少应过滤几次才能使产品达到市场要求?(已知:lg2=0.301 0,lg3=0.477 1)
21.(本小题满分12分)某地区2000年底沙漠面积为95万公顷,为了解该地区沙漠面积的变化情况,进行了连续5年的观测,并将每年年底的观测结果记录如下表,根据此表所给的信息进行预测:
(1)如果不采取任何措施,那么到2015年底,该地区的沙漠面积将大约变为多少万公顷?
(2)如果从2005年底后采取植树造林措施,每年改造0.6万公顷的沙漠,那么到哪一年年底该地区沙漠面积将减少到90万公顷?
22.(本小题满分12分)某电器公司生产A型电脑.2007年这种电脑每台平均生产成本为5 000元,并以纯利润20%确定出厂价,从2008年开始,公司通过更新设备和加强管理,使生产成本逐年降低,到2011年,尽管A型电脑出厂价仅是2007年出厂价的80%,但却实现了 50%纯利润的高效益.
(1)求2011年每台A型电脑的生产成本;
(2)以2007年生产成本为基数,求2007~2011年生产成本平均每年降低的百分率(精确到1%,注:≈2.236,≈2.449).
观测时间
2001年底
2002年底
2003年底
2004年底
2005年底
比原有面
积增加数
(万公顷)
0.200 0
0.400 0
0.600 1
0.799 9
1.000 1
详解答案
1[答案] C
[解析]当log3(x-1)=0时,x-1=1,∴x=2,故③错,其余都对.
2[答案] D
[解析] 如图(1)和(2)都满足题设条件.
3[答案] C
[解析] 由条件知f(-1)=0,∴b=a,∴g(x)=ax2+bx=ax(x+1)的零点为0和-1.
4[答案] B
[解析] ∵f(1)=-1<0,f(2)=lg2>0
∴f(x)在(1,2)内必有零点.
5[答案] C
[解析] 两次购物标价款:168+=168+470=638(元),
实际应付款:500×0.9+138×0.7=546.6(元).
6[答案] B
[解析] 当x≤1时 2-x=∴x=(舍)
当x>1时log81x=∴x=3,故选B.
7[答案] A
[解析] 令g(x)=2x+b-1,则函数g(x)为增函数,又由图象可知,函数f(x)为增函数,
∴a>1,又当x=0时,-1∴-18[答案] D
[解析] 机器人程序为前进3步、后退2步,则P(3)=3,P(5)=1均正确,即5步等于前进了一个单位长度,
∴P(2 003)=P(2 000)+P(3)=403,
P(2 005)=P(2 000)+P(5)=401,
∴P(2 003)>P(2 005)正确.
又P(2 007)=P(2 005)+P(2)=403,
P(2 008)=P(2 005)+P(3)=404,
∴P(2 007)>P(2 008)错误.
9[答案] B
[解析] 由于过(1,2)点,排除C、D;由图象与直线y=4无限接近,但到达不了,即y<4知排除A,∴选B.
10[答案] C
[解析] 由表可知f(x)的两个零点为-1和3,当-1<x<3时f(x)取正值∴使ax2+bx+c>0成立的x的取值范围是(-1,3).
11[答案] C
[解析] 由4x-3×2x+2=0,得(2x)2-3×2x+2=0,解得2x=2,或2x=1,∴x=0,或x=1.
12[答案] A
[解析] 方程mx-x-m=0有两个不同实数根,等价于函数y=mx与y=x+m的图象有两个不同的交点.显然当m>1时,如图(1)有两个不同交点当0<m<1时,如图(2)有且仅有一个交点.故选A.
13[答案] ①⑤
[解析] f(x)的图象是将函数y=x(x-1)(x+1)的图象向上平移0.01个单位得到.故f(x)的图象与x轴有三个交点,它们分别在区间(-
∞,-1),(0,)和(,1)内,故只有①⑤正确.
14[答案] 3
[解析] 如图,A(2天)→C(x)天B(5天)D(4天)
设工程所用总天数为f(x),则由题意得:
当x≤3时,f(x)=5+4=9,
当x>3时,f(x)=2+x+4=6+x,
∴f(x)=,
∵工程所用总天数f(x)=9,
∴x≤3,∴x最大值为3.
15[答案] (-,)
[解析] 由条件知∴
由得,或.
16[答案] -1或.
[解析] 由条件知或
∴x=-1或x=
17[解析] 不存在,因为当x<0时,->0
∴x2->0恒成立,故不存在x∈(-∞,0),使x2-=0.
18[解析] 设每天从报社买进x份报纸,每月获得的总利润为y元,则依题意有
y=0.10(20x+10×250)-0.15×10(x-250)
=0.5x+625,x∈[250,400].
该函数在[250,400]上单调递增,所以x=400时,ymax=825(元).
答:摊主每天从报社买进400份时,每月所获得的利润最大,最大利润为825元.
19[解析] 设f(x)=x2-2ax+2+a
(1)∵两根都大于1,
∴,解得2(2)∵方程一根大于1,一根小于1,
∴f(1)<0 ∴a>3.
20[解析] 设过滤n次,则·n≤
即n≤,∴n≥=≈7.4
又∵n∈N,
∴n≥8,即至少要过滤8次才能达到市场要求.
21[解析] (1)由表观察知,沙漠面积增加数y与第x年年底之间
的图象近似地为一次函数y=kx+b的图象.将x=1,y=0.2与x=2,y=0.4代入y=kx+b,求得k=0.2,b=0,所以y=0.2x(x∈N).因为原有沙漠面积为95万公顷,则到2015年底沙漠面积大约为95+0.2×15=98(万公顷).
(2)设从2011年算起,第x年年底该地区沙漠面积能减少到90万公顷.
由题意,得95+0.2x-0.6(x-5)=90,
解得x=20(年).故到2020年底,该地区沙漠面积减少到90万公顷.
22[解析] (1)设2011年每台电脑的生产成本为x元,依据题意,有
x(1+50%)=5000×(1+20%)×80%,
解得x=3 200(元).
(2)设2007~2011年间每年平均生产成本降低的百分率为y,
则依据题意,得5000(1-y)4=3 200,
解得y1=1-,y2=1+(舍去).
所以y=1-≈0.11=11%.
所以,2011年每台电脑的生产成本为3200元,2007年到2011年生产成本平均每年降低11%.
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分。考试时间120分钟。
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.给出下列四个命题:①函数f(x)=3x-6的零点是2;②函数f(x)=x2+4x+4的零点是-2;③函数f(x)=log3(x-1)的零点是1;④函数f(x)=2x-1的零点是0.其中正确的个数为( )
A.1 B.2 C.3 D.4
2.若函数y=f(x)在区间[0,4]上的图象是连续不断的曲线,且方程f(x)=0在(0,4)内仅有一个实数根,则f(0)·f(4)的值( )
A.大于0 B.小于0
C.等于0 D.无法判断
3.函数f(x)=ax+b的零点是-1(a≠0),则函数g(x)=ax2+bx的零点是( )
A.-1 B.0
C.-1和0 D.1和0
4.方程lgx+x-2=0一定有解的区间是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
5.某商场对顾客实行购物优惠活动,规定一次购物付款总额,
①如果不超过200元,则不予优惠.
②如果超过200元,但不超过500元,则按标准价给予9折优惠.
③如果超过500元,则其500元按第②条给予优惠,超过500元的部分给予7折优惠.
某人两次去购物,分别付款168元和423元,假设他只去一次购买上述同样的商品,则应付款是( )
A.413.7元 B.513.6元
C.546.6元 D.548.7元
6.设函数f(x)=,则方程f(x)=的解为( )
A. B.3
C.3或 D.无解
7.(08·山东文)已知函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a、b满足的关系是( )
A.0
A.P(3)=3 B.P(5)=1
C.P(2 003)>P(2 005) D.P(2 007)>P(2 008)
9.已知函数f(x)的图象如图,则它的一个可能的解析式为( )
A.y=2 B.y=4-
C.y=log3(x+1) D.y=x (x≥0)
10.已知二次函数f(x)=ax2+bx+c(x∈R)的部分对应值如表.
x
-3
-2
-1
0
1
2
3
4
5
…
y
-24
-10
0
6
8
6
0
-10
-24
…
则使ax2+bx+c>0成立的x的取值范围是( )
A.(-10,-1)∪(1+∞)
B.(-∞,-1)∪(3+∞)
C.(-1,3)
D.(0,+∞)
11.方程4x-3×2x+2=0的根的个数是( )
A.0 B.1 C.2 D.3
12.若方程mx-x-m=0(m>0,且m≠1)有两个不同实数根,则m的取值范围是( )
A.m>1 B.0<m<1
C.m>0 D.m>2
第
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.已知y=x(x-1)(x+1)的图象如图所示.令f(x)=x(x-1)(x+1)+0.01,则下列关于f(x)=0的解叙述正确的是________.
①有三个实根;
②x>1时恰有一实根;
③当0<x<1时恰有一实根;
④当-1<x<0时恰有一实根;
⑤当x<-1时恰有一实根(有且仅有一实根).
14.某工程由A、B、C、D四道工序完成,完成它们需用的时间依次2、5、x、4天,四道工序的先后顺序及相互关系是:A、B可以同时开工;A完成后,C可以开工;B、C完成后,D可以开工,若完成该工程总时间数为9天,则完成工序C需要的天数x最大为________.
15.已知抛物线y=ax2与直线y=kx+1交于两点,其中一点坐标为(1,4),则另一个点的坐标为______.
16.已知函数f(x)=,则方程f(x)=的解为________.
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本题满分10分)方程x2-=0在(-∞,0)内是否存在实数解?并说明理由.
18.(本题满分12分)北京市的一家报刊摊点,从报社买进《北京日报》的价格是每份0.20元,卖出的价格是每份0.30元,卖不掉的报纸可以以每份0.05元的价格退回报社.在一个月(30天计算)里,有20天每天可卖出400份,其余10天每天只能卖出250份,但每天从报社买进的份数必须相同,这个摊主每天从报社买进多少份,才能使每月所获的利润最大?并计算他一个月最多可赚得多少元?
19.(本题满分12分)若关于x的方程x2-2ax+2+a=0有两个不相等的实根,求分别满足下列条件的a的取值范围.
(1)方程两根都大于1;
(2)方程一根大于1,另一根小于1.
20.(本题满分12分)某化工厂生产的一种溶液,按市场要求,杂质含量不能超过0.1%.若初时含杂质2%,每过滤一次可使杂质含量减少,问至少应过滤几次才能使产品达到市场要求?(已知:lg2=0.301 0,lg3=0.477 1)
21.(本小题满分12分)某地区2000年底沙漠面积为95万公顷,为了解该地区沙漠面积的变化情况,进行了连续5年的观测,并将每年年底的观测结果记录如下表,根据此表所给的信息进行预测:
(1)如果不采取任何措施,那么到2015年底,该地区的沙漠面积将大约变为多少万公顷?
(2)如果从2005年底后采取植树造林措施,每年改造0.6万公顷的沙漠,那么到哪一年年底该地区沙漠面积将减少到90万公顷?
22.(本小题满分12分)某电器公司生产A型电脑.2007年这种电脑每台平均生产成本为5 000元,并以纯利润20%确定出厂价,从2008年开始,公司通过更新设备和加强管理,使生产成本逐年降低,到2011年,尽管A型电脑出厂价仅是2007年出厂价的80%,但却实现了 50%纯利润的高效益.
(1)求2011年每台A型电脑的生产成本;
(2)以2007年生产成本为基数,求2007~2011年生产成本平均每年降低的百分率(精确到1%,注:≈2.236,≈2.449).
观测时间
2001年底
2002年底
2003年底
2004年底
2005年底
比原有面
积增加数
(万公顷)
0.200 0
0.400 0
0.600 1
0.799 9
1.000 1
详解答案
1[答案] C
[解析]当log3(x-1)=0时,x-1=1,∴x=2,故③错,其余都对.
2[答案] D
[解析] 如图(1)和(2)都满足题设条件.
3[答案] C
[解析] 由条件知f(-1)=0,∴b=a,∴g(x)=ax2+bx=ax(x+1)的零点为0和-1.
4[答案] B
[解析] ∵f(1)=-1<0,f(2)=lg2>0
∴f(x)在(1,2)内必有零点.
5[答案] C
[解析] 两次购物标价款:168+=168+470=638(元),
实际应付款:500×0.9+138×0.7=546.6(元).
6[答案] B
[解析] 当x≤1时 2-x=∴x=(舍)
当x>1时log81x=∴x=3,故选B.
7[答案] A
[解析] 令g(x)=2x+b-1,则函数g(x)为增函数,又由图象可知,函数f(x)为增函数,
∴a>1,又当x=0时,-1
[解析] 机器人程序为前进3步、后退2步,则P(3)=3,P(5)=1均正确,即5步等于前进了一个单位长度,
∴P(2 003)=P(2 000)+P(3)=403,
P(2 005)=P(2 000)+P(5)=401,
∴P(2 003)>P(2 005)正确.
又P(2 007)=P(2 005)+P(2)=403,
P(2 008)=P(2 005)+P(3)=404,
∴P(2 007)>P(2 008)错误.
9[答案] B
[解析] 由于过(1,2)点,排除C、D;由图象与直线y=4无限接近,但到达不了,即y<4知排除A,∴选B.
10[答案] C
[解析] 由表可知f(x)的两个零点为-1和3,当-1<x<3时f(x)取正值∴使ax2+bx+c>0成立的x的取值范围是(-1,3).
11[答案] C
[解析] 由4x-3×2x+2=0,得(2x)2-3×2x+2=0,解得2x=2,或2x=1,∴x=0,或x=1.
12[答案] A
[解析] 方程mx-x-m=0有两个不同实数根,等价于函数y=mx与y=x+m的图象有两个不同的交点.显然当m>1时,如图(1)有两个不同交点当0<m<1时,如图(2)有且仅有一个交点.故选A.
13[答案] ①⑤
[解析] f(x)的图象是将函数y=x(x-1)(x+1)的图象向上平移0.01个单位得到.故f(x)的图象与x轴有三个交点,它们分别在区间(-
∞,-1),(0,)和(,1)内,故只有①⑤正确.
14[答案] 3
[解析] 如图,A(2天)→C(x)天B(5天)D(4天)
设工程所用总天数为f(x),则由题意得:
当x≤3时,f(x)=5+4=9,
当x>3时,f(x)=2+x+4=6+x,
∴f(x)=,
∵工程所用总天数f(x)=9,
∴x≤3,∴x最大值为3.
15[答案] (-,)
[解析] 由条件知∴
由得,或.
16[答案] -1或.
[解析] 由条件知或
∴x=-1或x=
17[解析] 不存在,因为当x<0时,->0
∴x2->0恒成立,故不存在x∈(-∞,0),使x2-=0.
18[解析] 设每天从报社买进x份报纸,每月获得的总利润为y元,则依题意有
y=0.10(20x+10×250)-0.15×10(x-250)
=0.5x+625,x∈[250,400].
该函数在[250,400]上单调递增,所以x=400时,ymax=825(元).
答:摊主每天从报社买进400份时,每月所获得的利润最大,最大利润为825元.
19[解析] 设f(x)=x2-2ax+2+a
(1)∵两根都大于1,
∴,解得2
∴f(1)<0 ∴a>3.
20[解析] 设过滤n次,则·n≤
即n≤,∴n≥=≈7.4
又∵n∈N,
∴n≥8,即至少要过滤8次才能达到市场要求.
21[解析] (1)由表观察知,沙漠面积增加数y与第x年年底之间
的图象近似地为一次函数y=kx+b的图象.将x=1,y=0.2与x=2,y=0.4代入y=kx+b,求得k=0.2,b=0,所以y=0.2x(x∈N).因为原有沙漠面积为95万公顷,则到2015年底沙漠面积大约为95+0.2×15=98(万公顷).
(2)设从2011年算起,第x年年底该地区沙漠面积能减少到90万公顷.
由题意,得95+0.2x-0.6(x-5)=90,
解得x=20(年).故到2020年底,该地区沙漠面积减少到90万公顷.
22[解析] (1)设2011年每台电脑的生产成本为x元,依据题意,有
x(1+50%)=5000×(1+20%)×80%,
解得x=3 200(元).
(2)设2007~2011年间每年平均生产成本降低的百分率为y,
则依据题意,得5000(1-y)4=3 200,
解得y1=1-,y2=1+(舍去).
所以y=1-≈0.11=11%.
所以,2011年每台电脑的生产成本为3200元,2007年到2011年生产成本平均每年降低11%.
