2021-2022学年人教版数学八年级下册16.2.1二次根式的乘法 课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册16.2.1二次根式的乘法 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-01 17:02:09 | ||
图片预览





文档简介
(共19张PPT)
16.2.1
二次根式的乘法
第十六章 二次根式
人教版八年级下册
学习目标
1.理解二次根式的乘法法则.(重点)
2.会运用二次根式的乘法法则和积的算术平方根的性质进行简单运算.(难点)
情景引入
问题:小明看见商店墙上贴着一张长方形新年海报(长宽如图所示,单位:cm),他想计算出它的面积,你能帮帮他吗?
这个结果能接着化简吗?
探究新知
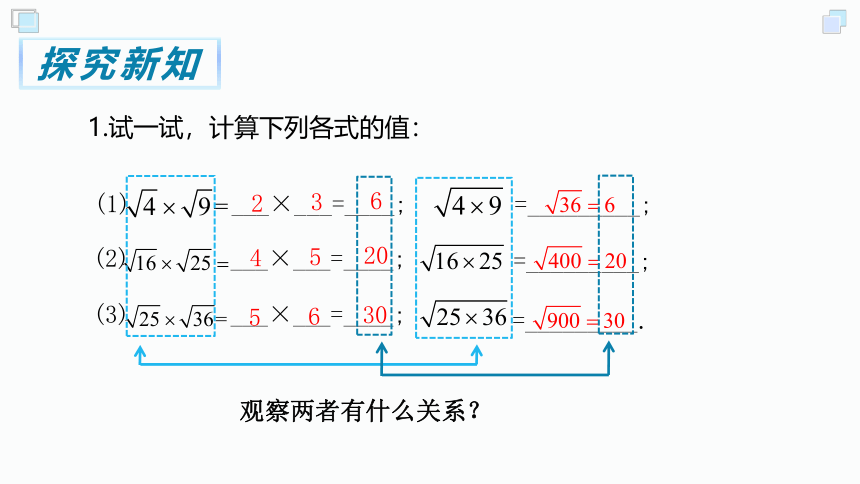
1.试一试,计算下列各式的值:
(1) ___×___=____;
=_________;
(2) ___×___=____;
(3) ___×___=____;
=_________;
=_________.
2
3
6
4
5
20
5
6
30
观察两者有什么关系?
探究新知
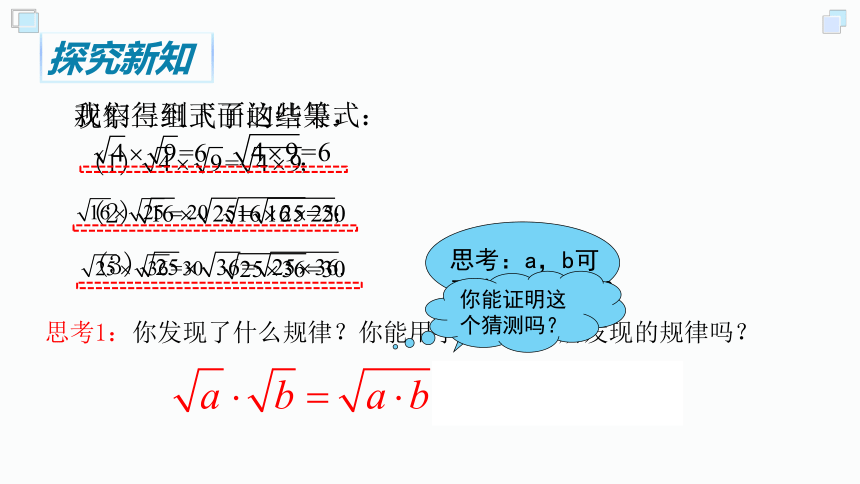
观察三组式子的结果,
(1)
(2)
(3)
思考1:你发现了什么规律?你能用字母表示你所发现的规律吗?
思考:a,b可否为任意实数?
我们得到下面这些等式:
你能证明这个猜测吗?
求证:
证明:根据积的乘方法则,有
∴
就是ab算术平方根.
又∵ 表示ab算术平方根,
∴ .
证一证
一般地,对于二次根式的乘法是
语言表述:
算术平方根的积等于各个被开方数积的算术平方根.
二次根式的乘法法则:
注意:a,b都必须是非负数.
探究新知
即二次根式相乘,________不变,________相乘.
根指数
被开方数
例1 计算:
例题精讲
解:
例1 计算:
例题精讲
解:
★ 二次根式乘法法则推广:
例2 计算:
解:
当二次根式根号外的因数不为1时,可类比单项式乘单项式的法则计算,即 .
分析:你还记得单项式乘单项式法则吗?
试回顾如何计算3a2·2a3= .
6a5
例题精讲
归纳
等式左右交换:
(a≥0,b≥0)
(a≥0,b≥0)
一般的:
这个性质也称为
“积的算术平方根的性质”
我们可以运用它来进行二次根式的解题和化简.
语言表述:积的算术平方根,等于积中各因式的算术平方根的积.
探究新知
例3 化简:
(1) ;(2)
(2)中4a2b3含有像4,a2,b2,这样开的尽方的因数或因式,把它们开方后移到根号外.
解:(1) ;
(2)
例题精讲
巩固训练
【变式题】 化简:
化简二次根式的步骤:
1.分解:将被开方数可能分解因数(因式)成几个平方数(式).
3.化简:将平方项应用 化简.
2.化积:应用
归纳总结
问题解决
问题:小明看见商店墙上贴着一张长方形新年海报(长宽如图所示,单位:cm),他想计算出它的面积,你能帮帮他吗?
课堂小结
1.二次根式的乘法法则是什么
应用时需要注意什么?
2.应用积的算术平方根的性质化简的步骤是什么?
当堂检测
当堂检测
教材10页习题16.2第1、3、6、7题.
课后作业
16.2.1
二次根式的乘法
第十六章 二次根式
人教版八年级下册
学习目标
1.理解二次根式的乘法法则.(重点)
2.会运用二次根式的乘法法则和积的算术平方根的性质进行简单运算.(难点)
情景引入
问题:小明看见商店墙上贴着一张长方形新年海报(长宽如图所示,单位:cm),他想计算出它的面积,你能帮帮他吗?
这个结果能接着化简吗?
探究新知
1.试一试,计算下列各式的值:
(1) ___×___=____;
=_________;
(2) ___×___=____;
(3) ___×___=____;
=_________;
=_________.
2
3
6
4
5
20
5
6
30
观察两者有什么关系?
探究新知
观察三组式子的结果,
(1)
(2)
(3)
思考1:你发现了什么规律?你能用字母表示你所发现的规律吗?
思考:a,b可否为任意实数?
我们得到下面这些等式:
你能证明这个猜测吗?
求证:
证明:根据积的乘方法则,有
∴
就是ab算术平方根.
又∵ 表示ab算术平方根,
∴ .
证一证
一般地,对于二次根式的乘法是
语言表述:
算术平方根的积等于各个被开方数积的算术平方根.
二次根式的乘法法则:
注意:a,b都必须是非负数.
探究新知
即二次根式相乘,________不变,________相乘.
根指数
被开方数
例1 计算:
例题精讲
解:
例1 计算:
例题精讲
解:
★ 二次根式乘法法则推广:
例2 计算:
解:
当二次根式根号外的因数不为1时,可类比单项式乘单项式的法则计算,即 .
分析:你还记得单项式乘单项式法则吗?
试回顾如何计算3a2·2a3= .
6a5
例题精讲
归纳
等式左右交换:
(a≥0,b≥0)
(a≥0,b≥0)
一般的:
这个性质也称为
“积的算术平方根的性质”
我们可以运用它来进行二次根式的解题和化简.
语言表述:积的算术平方根,等于积中各因式的算术平方根的积.
探究新知
例3 化简:
(1) ;(2)
(2)中4a2b3含有像4,a2,b2,这样开的尽方的因数或因式,把它们开方后移到根号外.
解:(1) ;
(2)
例题精讲
巩固训练
【变式题】 化简:
化简二次根式的步骤:
1.分解:将被开方数可能分解因数(因式)成几个平方数(式).
3.化简:将平方项应用 化简.
2.化积:应用
归纳总结
问题解决
问题:小明看见商店墙上贴着一张长方形新年海报(长宽如图所示,单位:cm),他想计算出它的面积,你能帮帮他吗?
课堂小结
1.二次根式的乘法法则是什么
应用时需要注意什么?
2.应用积的算术平方根的性质化简的步骤是什么?
当堂检测
当堂检测
教材10页习题16.2第1、3、6、7题.
课后作业
