2021-2022学年人教版七年级数学下册课件5.3 平行线的性质(共17张PPT)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册课件5.3 平行线的性质(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 623.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-01 17:03:09 | ||
图片预览



文档简介
(共17张PPT)
5.3平行线的性质
A
B
P
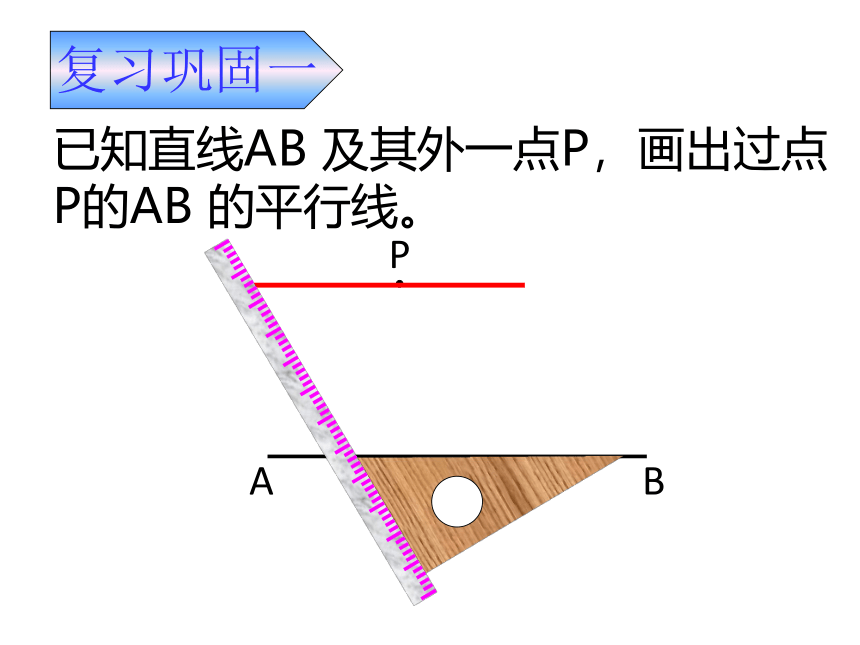
已知直线AB 及其外一点P,画出过点P的AB 的平行线。
复习巩固一
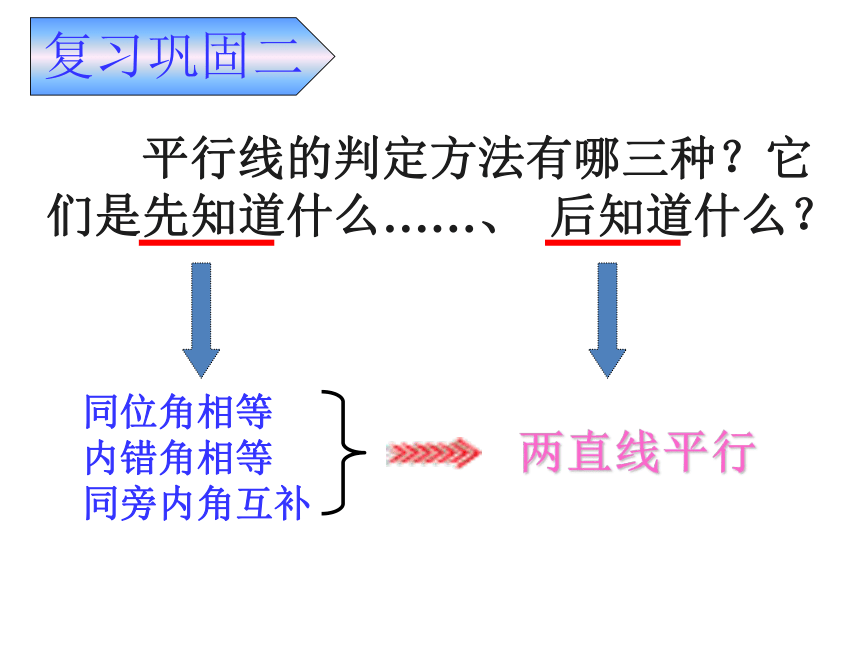
平行线的判定方法有哪三种?它
们是先知道什么……、 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
复习巩固二
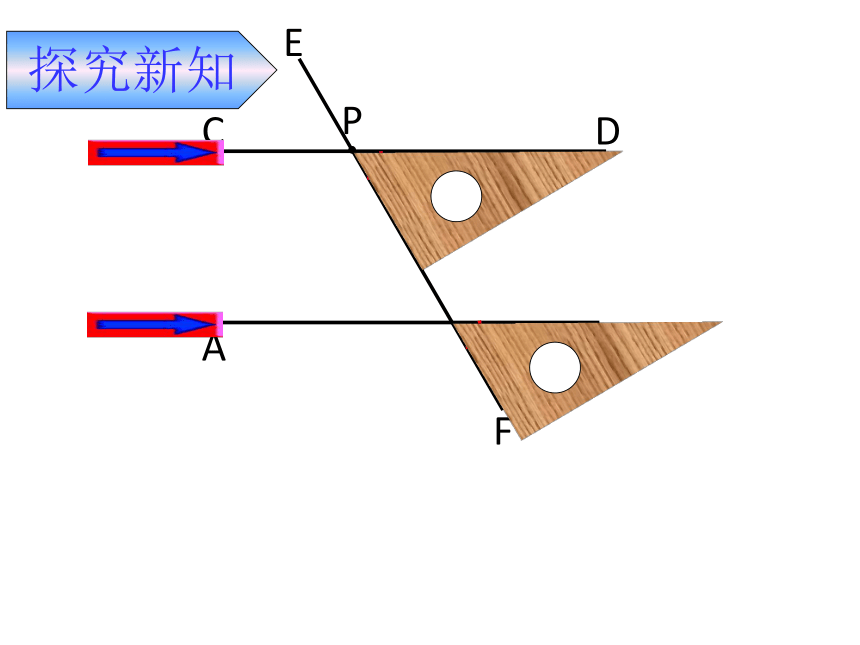
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
探究新知
A
B
P
C
D
E
F
2
1
探究新知
结论
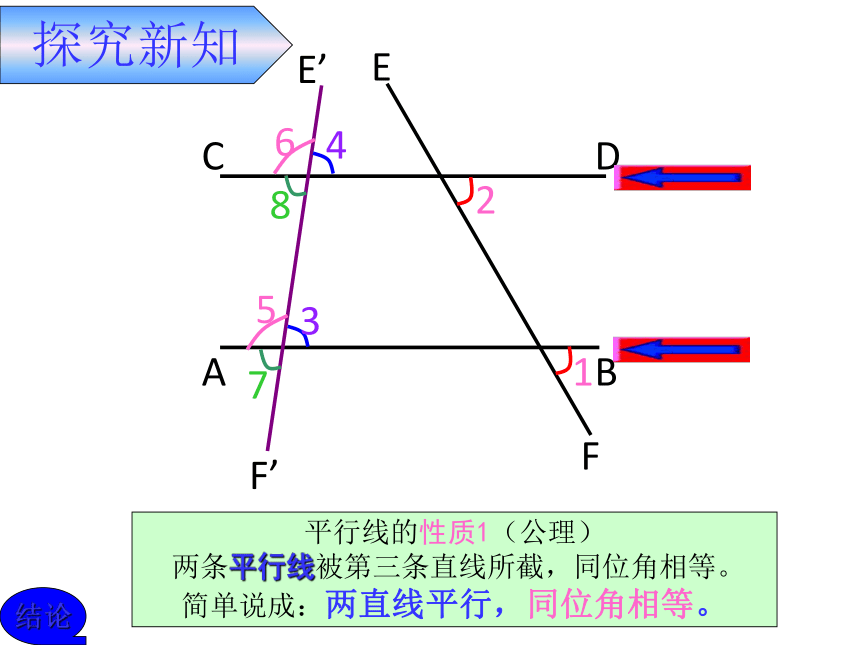
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
探究新知
A
B
C
D
E
F
2
1
E’
F’
3
4
5
6
8
7
结论
探究新知
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
a//b (已知)
1= 2 (两直线平行,同位角相等)
又 1= 3(对顶角相等)
3= 2(等量代换)
1
2
3
a
b
思考
回答
如图,已知:a// b
那么 3与 2有什么关系?
平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。
结论
探究新知
c
2
3
1
b
a
解: a//b (已知)
1= 2(两直线平行,同位角相等)
1+ 3=180°(邻补角定义)
2+ 3=180°(等量代换)
如图:已知a//b,那么 2与 3有什么关系呢?
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
探究新知
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
精彩回放
解:∵AD//BC (已知)
∴ A + B=180°
(两直线平行,同旁内角互补)
即 B= 180 °- A =180 ° -115 ° =65 °
∵AD//BC (已知)
∴ D+ C=180 °
(两直线平行,同旁内角互补)
即 C=180 °- D =180 ° -100 ° =80 °
答:梯形的另外两个角分别为65 ° 、80 ° 。
例1
C
B
A
D
如图是梯形有上底的一部分。 已经量得 A= 115°,
D=100°,梯形另外两个角各是多少度?
例题解析
C
B
解答:
∵AB∥CD
(已知)
∴∠B=∠C
(两直线平行,内错角相等)
又∵∠B=142°
∴∠B=∠C=142°
(已知)
(等量代换)
A
D
P.86EX.1
练习巩固
4
3
2
1
A
C
B
D
E
(1)∵AB∥CD
(已知)
∴∠1=∠2
(两直线平行,内错角相等)
又∵∠1=110°
∴∠1=∠2=110°
(已知)
(等量代换)
(2)∵AB∥CD
(已知)
∴∠1=∠3
(两直线平行,同位角相等)
又∵∠1=110°
∴∠1=∠3=110°
(已知)
(等量代换)
(3)∵AB∥CD
(已知)
∴∠1+∠4=180°
(两直线平行,同旁内角互补)
又∵∠1=110°
(已知)
∴110 ° +∠4=180°
(等量代换)
∴∠4=180°-110°=70°
(等式性质)
解答:
P.86EX.2
练习巩固
平行线的“判定”与“性质”有什么不同
对比梳理
已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。
2
1
D
C
B
A
如图: 1= 2(已知)
AD//
( )
BCD+ D=180
( )
BC
内错角相等,两直线平行
两直线平行,同旁内角互补
练习巩固
E
D
C
B
A
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
又∵∠ADE =∠B
(已证)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
解答:
P.86EX.3
练习巩固
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
复习回顾
巩固练习
课堂小结
课堂小结
5.3平行线的性质
A
B
P
已知直线AB 及其外一点P,画出过点P的AB 的平行线。
复习巩固一
平行线的判定方法有哪三种?它
们是先知道什么……、 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
复习巩固二
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
探究新知
A
B
P
C
D
E
F
2
1
探究新知
结论
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
探究新知
A
B
C
D
E
F
2
1
E’
F’
3
4
5
6
8
7
结论
探究新知
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
a//b (已知)
1= 2 (两直线平行,同位角相等)
又 1= 3(对顶角相等)
3= 2(等量代换)
1
2
3
a
b
思考
回答
如图,已知:a// b
那么 3与 2有什么关系?
平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。
结论
探究新知
c
2
3
1
b
a
解: a//b (已知)
1= 2(两直线平行,同位角相等)
1+ 3=180°(邻补角定义)
2+ 3=180°(等量代换)
如图:已知a//b,那么 2与 3有什么关系呢?
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
探究新知
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
精彩回放
解:∵AD//BC (已知)
∴ A + B=180°
(两直线平行,同旁内角互补)
即 B= 180 °- A =180 ° -115 ° =65 °
∵AD//BC (已知)
∴ D+ C=180 °
(两直线平行,同旁内角互补)
即 C=180 °- D =180 ° -100 ° =80 °
答:梯形的另外两个角分别为65 ° 、80 ° 。
例1
C
B
A
D
如图是梯形有上底的一部分。 已经量得 A= 115°,
D=100°,梯形另外两个角各是多少度?
例题解析
C
B
解答:
∵AB∥CD
(已知)
∴∠B=∠C
(两直线平行,内错角相等)
又∵∠B=142°
∴∠B=∠C=142°
(已知)
(等量代换)
A
D
P.86EX.1
练习巩固
4
3
2
1
A
C
B
D
E
(1)∵AB∥CD
(已知)
∴∠1=∠2
(两直线平行,内错角相等)
又∵∠1=110°
∴∠1=∠2=110°
(已知)
(等量代换)
(2)∵AB∥CD
(已知)
∴∠1=∠3
(两直线平行,同位角相等)
又∵∠1=110°
∴∠1=∠3=110°
(已知)
(等量代换)
(3)∵AB∥CD
(已知)
∴∠1+∠4=180°
(两直线平行,同旁内角互补)
又∵∠1=110°
(已知)
∴110 ° +∠4=180°
(等量代换)
∴∠4=180°-110°=70°
(等式性质)
解答:
P.86EX.2
练习巩固
平行线的“判定”与“性质”有什么不同
对比梳理
已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。
2
1
D
C
B
A
如图: 1= 2(已知)
AD//
( )
BCD+ D=180
( )
BC
内错角相等,两直线平行
两直线平行,同旁内角互补
练习巩固
E
D
C
B
A
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
又∵∠ADE =∠B
(已证)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
解答:
P.86EX.3
练习巩固
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
复习回顾
巩固练习
课堂小结
课堂小结
