2021-2022学年苏科版七年级下册数学7.5多边形的内角和与外角和 同步练习(word版含解析)
文档属性
| 名称 | 2021-2022学年苏科版七年级下册数学7.5多边形的内角和与外角和 同步练习(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 57.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-01 17:23:43 | ||
图片预览

文档简介
7.5多边形的内角和与外角和
一.选择题
1.若一个多边形的每一个外角都等于45°,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
2.一个多边形的外角和等于360°,则这个多边形的边数为( )
A.3 B.4
C.5 D.以上均有可能
3.如果一个多边形的外角和等于其内角和的2倍,那么这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
4.如图,∠BDC=100°,∠C=35°,∠A=28°,则∠B的度数是( )
A.43° B.33° C.47° D.37°
5.某多边形的内角和比外角和多180度,这个多边形的边数( )
A.3 B.4 C.5 D.6
6.如图,在六边形ABCDEF中,若∠1+∠2=90°,则∠3+∠4+∠5+∠6=( )
A.180° B.240° C.270° D.360°
7.若一个多边形的外角和是它内角和的,那么这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
8.若一个多边形的内角和等于1800°,这个多边形的边数是( )
A.6 B.8 C.10 D.12
9.一个多边形截去一个角后,得到的多边形的内角和为1980°,那么原来的多边形的边数为( )
A.12或13取14 B.13或14 C.12或13 D.13或14或15
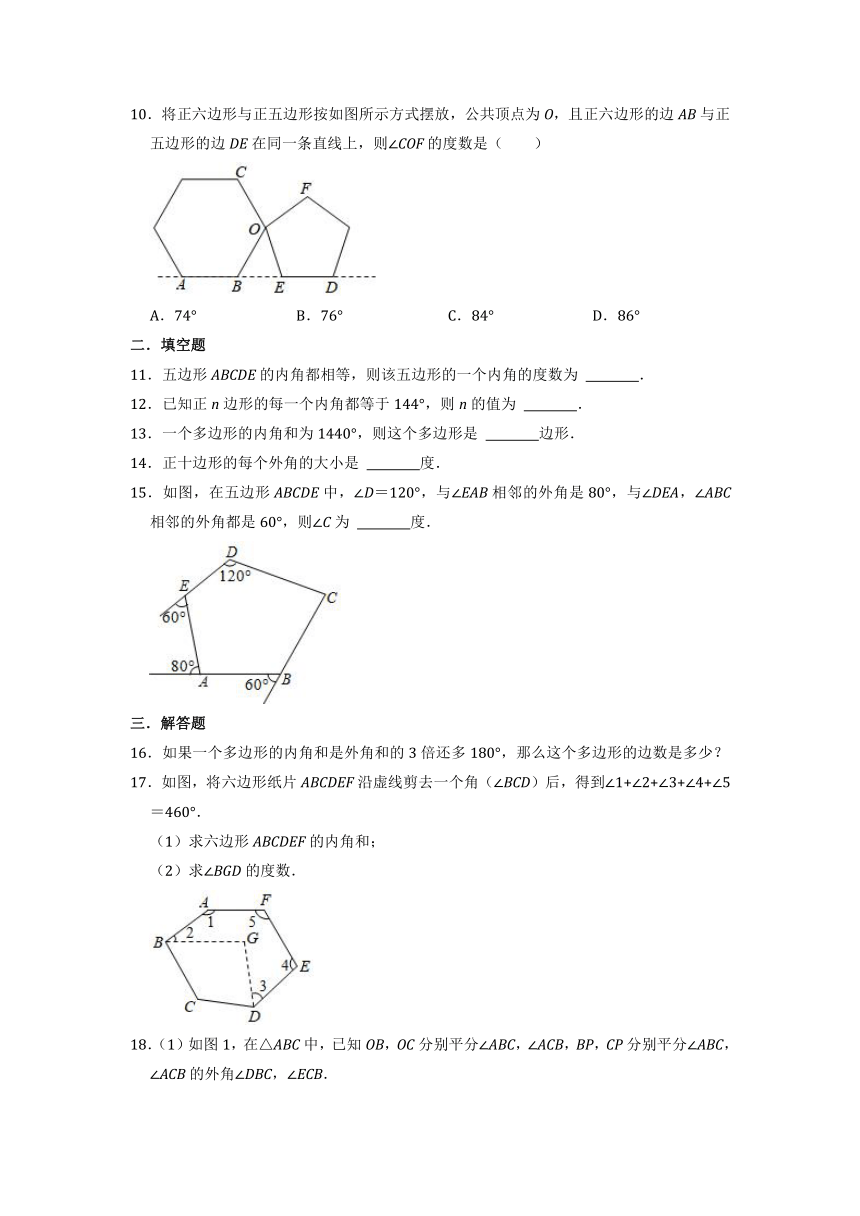
10.将正六边形与正五边形按如图所示方式摆放,公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠COF的度数是( )
A.74° B.76° C.84° D.86°
二.填空题
11.五边形ABCDE的内角都相等,则该五边形的一个内角的度数为 .
12.已知正n边形的每一个内角都等于144°,则n的值为 .
13.一个多边形的内角和为1440°,则这个多边形是 边形.
14.正十边形的每个外角的大小是 度.
15.如图,在五边形ABCDE中,∠D=120°,与∠EAB相邻的外角是80°,与∠DEA,∠ABC相邻的外角都是60°,则∠C为 度.
三.解答题
16.如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少?
17.如图,将六边形纸片ABCDEF沿虚线剪去一个角(∠BCD)后,得到∠1+∠2+∠3+∠4+∠5=460°.
(1)求六边形ABCDEF的内角和;
(2)求∠BGD的度数.
18.(1)如图1,在△ABC中,已知OB,OC分别平分∠ABC,∠ACB,BP,CP分别平分∠ABC,∠ACB的外角∠DBC,∠ECB.
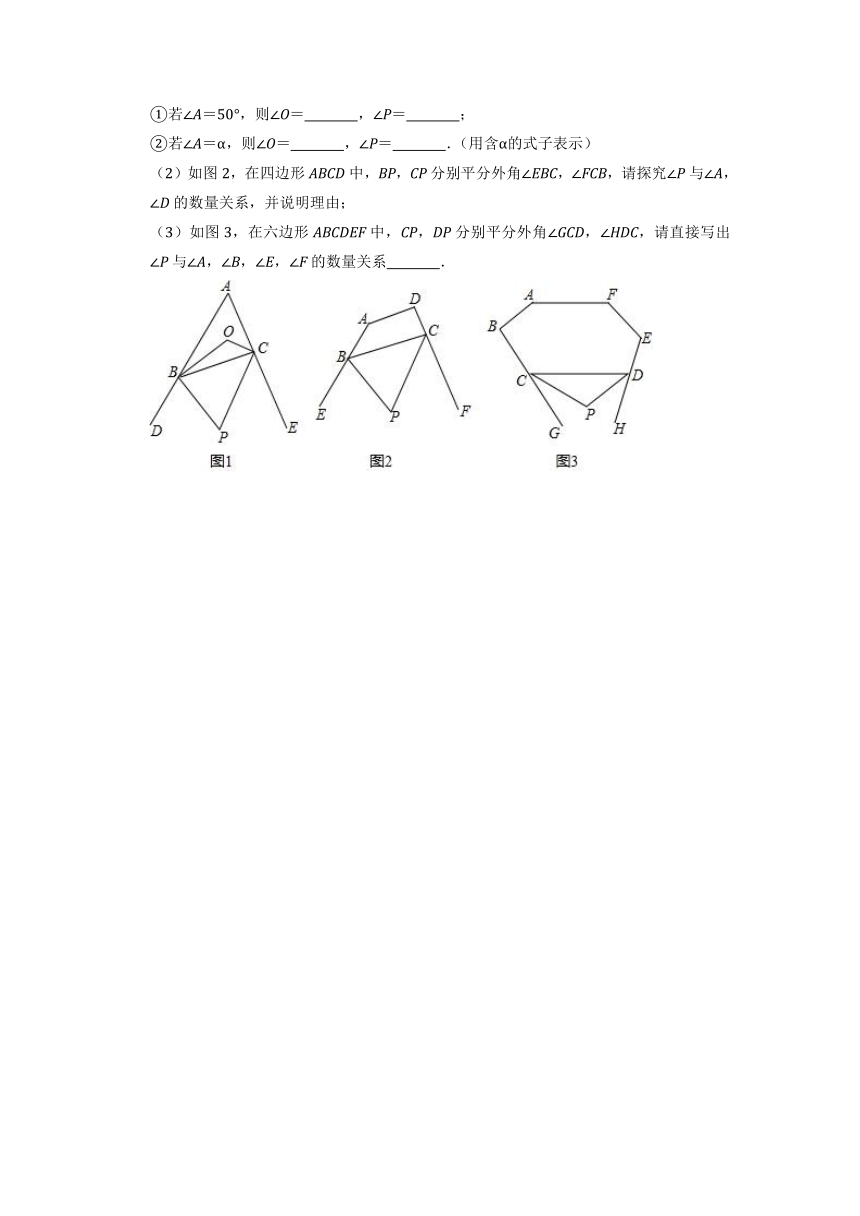
①若∠A=50°,则∠O= ,∠P= ;
②若∠A=α,则∠O= ,∠P= .(用含α的式子表示)
(2)如图2,在四边形ABCD中,BP,CP分别平分外角∠EBC,∠FCB,请探究∠P与∠A,∠D的数量关系,并说明理由;
(3)如图3,在六边形ABCDEF中,CP,DP分别平分外角∠GCD,∠HDC,请直接写出∠P与∠A,∠B,∠E,∠F的数量关系 .
参考答案
一.选择题
1.解:多边形的边数为360÷45=8,
所以这个多边形是八边形,
故选:D.
2.解:∵多边形的外角和等于360°,
∴这个多边形的边数不能确定.
故选:D.
3.解:设它的边数是n,根据题意得,
2(n﹣2) 180°=360°,
解得n=3.
故选:A.
4.解:延长BD交AC于点E,
∵∠BDC=∠C+∠BEC,∠BEC=∠A+∠B,
∴∠BCD=∠A+∠B+∠C,
∵∠BDC=100°,∠A=28°,∠C=35°,
∴∠B=100°﹣28°﹣35°=37°,
故选:D.
5.解:根据题意可得:
(n 2) 180°=360°+180°,
解得:n=5.
经检验n=5符合题意,
所以这个多边形的边数是5.
故选:C.
6.解:∵∠1+∠2+∠3+∠4+∠5+∠6=360°,
又∵∠1+∠2=90°,
∴∠3+∠4+∠5+∠6=360°﹣90°=270°,
故选:C.
7.解:根据题意可得:
(n 2) 180°=360°,
解得:n=5.
经检验n=5符合题意,
所以这个多边形是五边形.
故选:C.
8.解:设这个多边形是n边形,
根据题意得(n﹣2)×180=1800,
解得n=12,
∴这个多边形是12边形.
故选:D.
9.解:设新的多边形的边数为n,
∵新的多边形的内角和是1980°,
∴180(n﹣2)=1980,
解得:n=13,
∵一个多边形从某一个顶点出发截去一个角后所形成的新的多边形是十三边形,
∴原多边形的边数可能是:12或13或14.
故选:A.
10.解:由题意得:∠EOF=108°,∠BOC=120°,∠OEB=72°,∠OBE=60°,
∴∠BOE=180°﹣72°﹣60°=48°,
∴∠COF=360°﹣108°﹣48°﹣120°=84°,
故选:C.
二.填空题
11.解:360°÷5=72°,
180°﹣72°=108°.
故答案为:108°.
12.解:∵正n边形的每一个内角都等于144°,
∴每一个外角都是180﹣144=36(度),
∴n=360÷36=10.
故答案为:10.
13.解:设这个多边形的边数为n,
则(n﹣2)×180°=1440°,
解得:n=10,
即这个多边形是10边形,
故答案为:10.
14.解:∵正多边形的每个外角相等,
∴正十边形每个外角为360°÷10=36°.
故答案为:36.
15.解:在五边形ABCDE中,∠D=120°,与∠EAB相邻的外角是80°,与∠DEA,∠ABC相邻的外角都是60°,
∴∠EAB相邻的内角度数为:180°﹣80°=100°,
∴∠DEA相邻的内角度数为:180°﹣60°=120°,
∴∠ABC相邻的内角度数为:180°﹣60°=120°,
五边形的内角和=(5﹣2)×180°=540°,
∴∠C=540°﹣100°﹣120°﹣120°﹣120°=80°.
故答案为:80°.
三.解答题
16.解:设这个多边形的边数为n,根据题意,得
(n﹣2) 180=360×3+180,
解得:n=9.
则这个多边形的边数是9.
17.解:(1)六边形ABCDEF的内角和为:180°×(6﹣2)=720°;
(2)∵六边形ABCDEF的内角和为720°,∠1+∠2+∠3+∠4+∠5=460°,
∴∠GBC+∠C+∠CDG=720°﹣460°=260°,
∴∠BGD=360°﹣(∠GBC+∠C+∠CDG)=100°.
即∠BGD的度数是100°.
18.解:(1)①解:∠O=180°﹣∠OBC﹣∠OCB=180°﹣∠ABC﹣∠ACB=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=180°﹣(180°﹣50°)=115°;
∠P=180°﹣∠PBC﹣∠PCB=180°﹣∠DBC﹣∠ECB=180°﹣(∠DBC+∠ECB)=180°﹣(180°﹣∠ABC+180°﹣∠ACB)=180°﹣[360°﹣(∠ABC+∠ACB)]=180°﹣[360°﹣(180°﹣∠A)]=180°﹣[360°﹣(180°﹣50°)]=65°;
故答案为:115°;65°.
②解:∠O=180°﹣∠OBC﹣∠OCB=180°﹣∠ABC﹣∠ACB=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=180°﹣(180°﹣α)=90°+α;
∠P=180°﹣∠PBC﹣∠PCB=180°﹣∠DBC﹣∠ECB=180°﹣(∠DBC+∠ECB)=180°﹣(180°﹣∠ABC+180°﹣∠ACB)=180°﹣[360°﹣(∠ABC+∠ACB)]=180°﹣[360°﹣(180°﹣∠A)]=180°﹣[360°﹣(180°﹣α)]=90°﹣α;
故答案为:90°+α;90°﹣α,
(2)解:∠P=180°﹣(∠A+∠D).理由如下:
∠P=180°﹣(∠PBC+∠PCB)=180°﹣(∠EBC+∠FCB)=180°﹣[360°﹣(∠ABC+∠DCB)]=(∠ABC+∠DCB)=(360°﹣∠A﹣∠D)=180°﹣(∠A+∠D).
(3)∠P=180°﹣(∠GCD+∠HDC)=180°﹣(180°﹣∠BCD+180°﹣∠CDE)=(∠BCD+∠CDE)=[(6﹣2)×180°﹣(∠A+∠B+∠E+∠F)]=360°﹣(∠A+∠B+∠E+∠F).
故答案为:∠P=360°﹣(∠A+∠B+∠E+∠F)
一.选择题
1.若一个多边形的每一个外角都等于45°,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
2.一个多边形的外角和等于360°,则这个多边形的边数为( )
A.3 B.4
C.5 D.以上均有可能
3.如果一个多边形的外角和等于其内角和的2倍,那么这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
4.如图,∠BDC=100°,∠C=35°,∠A=28°,则∠B的度数是( )
A.43° B.33° C.47° D.37°
5.某多边形的内角和比外角和多180度,这个多边形的边数( )
A.3 B.4 C.5 D.6
6.如图,在六边形ABCDEF中,若∠1+∠2=90°,则∠3+∠4+∠5+∠6=( )
A.180° B.240° C.270° D.360°
7.若一个多边形的外角和是它内角和的,那么这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
8.若一个多边形的内角和等于1800°,这个多边形的边数是( )
A.6 B.8 C.10 D.12
9.一个多边形截去一个角后,得到的多边形的内角和为1980°,那么原来的多边形的边数为( )
A.12或13取14 B.13或14 C.12或13 D.13或14或15
10.将正六边形与正五边形按如图所示方式摆放,公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠COF的度数是( )
A.74° B.76° C.84° D.86°
二.填空题
11.五边形ABCDE的内角都相等,则该五边形的一个内角的度数为 .
12.已知正n边形的每一个内角都等于144°,则n的值为 .
13.一个多边形的内角和为1440°,则这个多边形是 边形.
14.正十边形的每个外角的大小是 度.
15.如图,在五边形ABCDE中,∠D=120°,与∠EAB相邻的外角是80°,与∠DEA,∠ABC相邻的外角都是60°,则∠C为 度.
三.解答题
16.如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少?
17.如图,将六边形纸片ABCDEF沿虚线剪去一个角(∠BCD)后,得到∠1+∠2+∠3+∠4+∠5=460°.
(1)求六边形ABCDEF的内角和;
(2)求∠BGD的度数.
18.(1)如图1,在△ABC中,已知OB,OC分别平分∠ABC,∠ACB,BP,CP分别平分∠ABC,∠ACB的外角∠DBC,∠ECB.
①若∠A=50°,则∠O= ,∠P= ;
②若∠A=α,则∠O= ,∠P= .(用含α的式子表示)
(2)如图2,在四边形ABCD中,BP,CP分别平分外角∠EBC,∠FCB,请探究∠P与∠A,∠D的数量关系,并说明理由;
(3)如图3,在六边形ABCDEF中,CP,DP分别平分外角∠GCD,∠HDC,请直接写出∠P与∠A,∠B,∠E,∠F的数量关系 .
参考答案
一.选择题
1.解:多边形的边数为360÷45=8,
所以这个多边形是八边形,
故选:D.
2.解:∵多边形的外角和等于360°,
∴这个多边形的边数不能确定.
故选:D.
3.解:设它的边数是n,根据题意得,
2(n﹣2) 180°=360°,
解得n=3.
故选:A.
4.解:延长BD交AC于点E,
∵∠BDC=∠C+∠BEC,∠BEC=∠A+∠B,
∴∠BCD=∠A+∠B+∠C,
∵∠BDC=100°,∠A=28°,∠C=35°,
∴∠B=100°﹣28°﹣35°=37°,
故选:D.
5.解:根据题意可得:
(n 2) 180°=360°+180°,
解得:n=5.
经检验n=5符合题意,
所以这个多边形的边数是5.
故选:C.
6.解:∵∠1+∠2+∠3+∠4+∠5+∠6=360°,
又∵∠1+∠2=90°,
∴∠3+∠4+∠5+∠6=360°﹣90°=270°,
故选:C.
7.解:根据题意可得:
(n 2) 180°=360°,
解得:n=5.
经检验n=5符合题意,
所以这个多边形是五边形.
故选:C.
8.解:设这个多边形是n边形,
根据题意得(n﹣2)×180=1800,
解得n=12,
∴这个多边形是12边形.
故选:D.
9.解:设新的多边形的边数为n,
∵新的多边形的内角和是1980°,
∴180(n﹣2)=1980,
解得:n=13,
∵一个多边形从某一个顶点出发截去一个角后所形成的新的多边形是十三边形,
∴原多边形的边数可能是:12或13或14.
故选:A.
10.解:由题意得:∠EOF=108°,∠BOC=120°,∠OEB=72°,∠OBE=60°,
∴∠BOE=180°﹣72°﹣60°=48°,
∴∠COF=360°﹣108°﹣48°﹣120°=84°,
故选:C.
二.填空题
11.解:360°÷5=72°,
180°﹣72°=108°.
故答案为:108°.
12.解:∵正n边形的每一个内角都等于144°,
∴每一个外角都是180﹣144=36(度),
∴n=360÷36=10.
故答案为:10.
13.解:设这个多边形的边数为n,
则(n﹣2)×180°=1440°,
解得:n=10,
即这个多边形是10边形,
故答案为:10.
14.解:∵正多边形的每个外角相等,
∴正十边形每个外角为360°÷10=36°.
故答案为:36.
15.解:在五边形ABCDE中,∠D=120°,与∠EAB相邻的外角是80°,与∠DEA,∠ABC相邻的外角都是60°,
∴∠EAB相邻的内角度数为:180°﹣80°=100°,
∴∠DEA相邻的内角度数为:180°﹣60°=120°,
∴∠ABC相邻的内角度数为:180°﹣60°=120°,
五边形的内角和=(5﹣2)×180°=540°,
∴∠C=540°﹣100°﹣120°﹣120°﹣120°=80°.
故答案为:80°.
三.解答题
16.解:设这个多边形的边数为n,根据题意,得
(n﹣2) 180=360×3+180,
解得:n=9.
则这个多边形的边数是9.
17.解:(1)六边形ABCDEF的内角和为:180°×(6﹣2)=720°;
(2)∵六边形ABCDEF的内角和为720°,∠1+∠2+∠3+∠4+∠5=460°,
∴∠GBC+∠C+∠CDG=720°﹣460°=260°,
∴∠BGD=360°﹣(∠GBC+∠C+∠CDG)=100°.
即∠BGD的度数是100°.
18.解:(1)①解:∠O=180°﹣∠OBC﹣∠OCB=180°﹣∠ABC﹣∠ACB=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=180°﹣(180°﹣50°)=115°;
∠P=180°﹣∠PBC﹣∠PCB=180°﹣∠DBC﹣∠ECB=180°﹣(∠DBC+∠ECB)=180°﹣(180°﹣∠ABC+180°﹣∠ACB)=180°﹣[360°﹣(∠ABC+∠ACB)]=180°﹣[360°﹣(180°﹣∠A)]=180°﹣[360°﹣(180°﹣50°)]=65°;
故答案为:115°;65°.
②解:∠O=180°﹣∠OBC﹣∠OCB=180°﹣∠ABC﹣∠ACB=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=180°﹣(180°﹣α)=90°+α;
∠P=180°﹣∠PBC﹣∠PCB=180°﹣∠DBC﹣∠ECB=180°﹣(∠DBC+∠ECB)=180°﹣(180°﹣∠ABC+180°﹣∠ACB)=180°﹣[360°﹣(∠ABC+∠ACB)]=180°﹣[360°﹣(180°﹣∠A)]=180°﹣[360°﹣(180°﹣α)]=90°﹣α;
故答案为:90°+α;90°﹣α,
(2)解:∠P=180°﹣(∠A+∠D).理由如下:
∠P=180°﹣(∠PBC+∠PCB)=180°﹣(∠EBC+∠FCB)=180°﹣[360°﹣(∠ABC+∠DCB)]=(∠ABC+∠DCB)=(360°﹣∠A﹣∠D)=180°﹣(∠A+∠D).
(3)∠P=180°﹣(∠GCD+∠HDC)=180°﹣(180°﹣∠BCD+180°﹣∠CDE)=(∠BCD+∠CDE)=[(6﹣2)×180°﹣(∠A+∠B+∠E+∠F)]=360°﹣(∠A+∠B+∠E+∠F).
故答案为:∠P=360°﹣(∠A+∠B+∠E+∠F)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
