2021-2022年人教版八年级数学下册20.2数据的波动程度同步课堂练习 (word版含解析)
文档属性
| 名称 | 2021-2022年人教版八年级数学下册20.2数据的波动程度同步课堂练习 (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 291.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 09:42:32 | ||
图片预览



文档简介
2021-2022年初中数学八年级下册同步(人教版)
20.2数据的波动程度-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若一组数据,0,2,4,的极差为7,则的值是( ).
A. B.6 C.7 D.6或
2.样本方差的计算公式S2=[(-30)2+(-30)]2+…+(-30)2]中,数字20和30分别表示样本中的( )
A.众数、中位数 B.方差、标准差
C.样本中数据的个数、平均数 D.样本中数据的个数、中位数
3.有一组数据7、11、12、7、7、8、11,下列说法错误的是( )
A.中位数是7 B.平均数是9 C.众数是7 D.极差为5
4.已知某运动队的甲、乙、丙、丁四名射击运动员平时训练的平均成绩(单位:环)以及方差(单位:环)如下表,现要选一名成绩优秀且稳定的队员参加某项比赛,则应选( )
甲 乙 丙 丁
9.0 9.0 9.5 9.5
0.5 2.2 1.7 0.5
A.甲 B.乙 C.丙 D.丁
5.如图所示,是小强同学根据某城区某天上午和下午各四个整时点的气温绘制成的折线统计图,根据统计图请回答:该天上午和下午气温比较稳定的是( )
A.上午 B.下午 C.上午与下午稳定情况相同 D.无法确定
6.如图是小明和小华射击成绩的统计图,两人都射击了10次,下列说法正确的是( )
A.小明成绩的方差比小华成绩的方差大 B.小明和小华成绩的众数相同
C.小明成绩的中位数比小华成绩的中位数大 D.小明和小华的平均成绩相同
二、填空题
7.随机从甲、乙两块试验田中各抽取株麦苗测量高度,计算平均数和方差的结果:,,,,则小麦长势比较整齐的试验田是_____________.
8.一组数据的极差为,方差为,则数据的极差为____,方差为___.
9.已知2,3,5,m,n五个数据的方差是2,那么3,4,6,m+1,n+1五个数据的方差是______.
10.已知一组数据-3,-2,1,3,6,x的中位数为1,则其方差为_________.
11.标准差:方差的算术平方根S=_________,叫做这组数据的 _________.
12.要从小华、小明两名射击运动员中选择一名运动员参加射击比赛,在赛前对他们进行了一次选拔赛,下图为小华、小明两人在选拔赛中各射击10次成绩的折线图和表示平均数的水平线.你认为应该选择______(填“小华”或“小明”)参加射击比赛;理由是__________.
三、解答题
13.某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如表所示.根据表中数据,你认为快餐公司应该选购哪家加工厂的鸡腿?
甲 74 74 75 74 76 73 76 73 76 75 78 77 74 72 73
乙 75 73 79 72 76 71 73 72 78 74 77 78 80 71 75
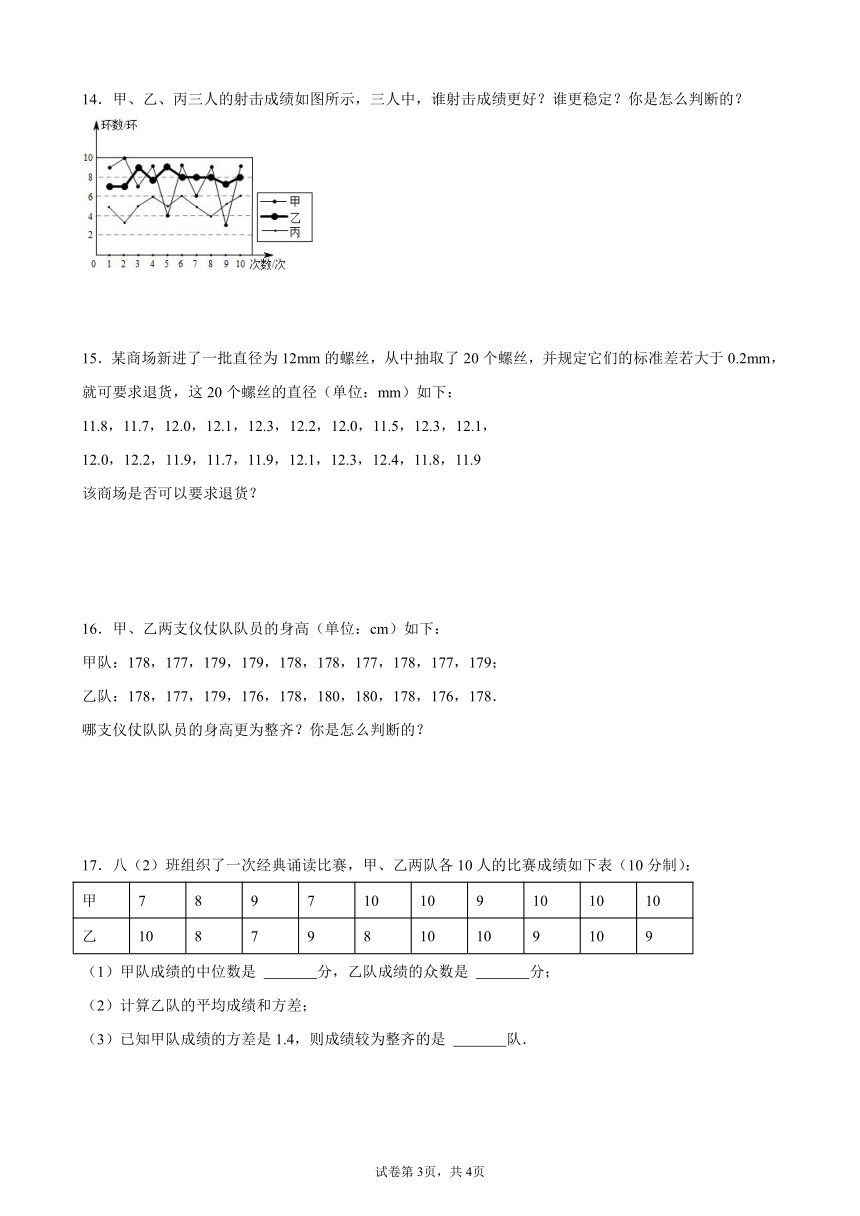
14.甲、乙、丙三人的射击成绩如图所示,三人中,谁射击成绩更好?谁更稳定?你是怎么判断的?
15.某商场新进了一批直径为12mm的螺丝,从中抽取了20个螺丝,并规定它们的标准差若大于0.2mm,就可要求退货,这20个螺丝的直径(单位:mm)如下:
11.8,11.7,12.0,12.1,12.3,12.2,12.0,11.5,12.3,12.1,
12.0,12.2,11.9,11.7,11.9,12.1,12.3,12.4,11.8,11.9
该商场是否可以要求退货?
16.甲、乙两支仪仗队队员的身高(单位:cm)如下:
甲队:178,177,179,179,178,178,177,178,177,179;
乙队:178,177,179,176,178,180,180,178,176,178.
哪支仪仗队队员的身高更为整齐?你是怎么判断的?
17.八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
18.我县某中学七、八年级各选派10名选手参加学校举办的“爱我太康”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别 平均分 中位数 方差 合格率 优秀率
七年级 6.7 m 3.41 90% n
八年级 7.1 7.5 1.69 80% 10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【解析】解:根据极差的计算法则可得:x-(-1)=7或4-x=7,
解得:x=6或x=-3.
故选D
2.C
【解析】解:∵S2=[(-30)2+(-30)]2+…+(-30)2]
∴20是样本中数据的个数,30是这组数据的平均数.
故选C.
3.A
【解析】这组数据按照从小到大的顺序排列为:7.7.7.8.11.11.12,
则中位数为8,平均数为,众数为7,极差为,
故选A.
4.D
【解析】解:
又
丁的成绩优秀且最稳定,
故选:D.
5.B
【解析】解: 上=(18+19+21+22)÷4=20,
下=(22.5+20+19+18.5)÷4=20,
S2上=[(18-20)2+(19-20)2+(21-20)2+(22-20)2]÷4=2.5,
S2下=[(22.5-20)2+(20-20)2+(19-20)2+(18.5-20)2]÷4=2.375,
∵S2上>S2下,
∴下午的气温更稳定.
故选B.
6.D
【解析】解:小华成绩是:8,7,3,8,3,10,6,10,8,8,从小到大排序为3,3,6,7,8,8,8,8,10,10,
中位数是8,众数是8,平均数,
方差
小明成绩是8,9,8,8,7,8,7,6,7,8,从小到大排序为6,7,7,7,8,8,8,8,8,9,
中位数是8,众数是8,平均数,
方差
A.根据折线统计图可知,小明的成绩波动较小,小华成绩的波动较大,故小明的成绩的方差较小;故选项A不正确;
B.小明和小华的成绩中,8环出现的次数均最多,故众数都是8环;故选项B正确;
C.将小明和小华的成绩分别按大小顺序排列,每组数据的中间两个数都是8,故中位数都是8环;故选项C不正确;
D.小明的平均成绩为7.6环,小华的平均成绩为7.1环,故选项D不正确.
故选D.
7.甲
【解析】解:由方差的意义,观察数据可知,
∵,
∴甲块试验田的方差小,
故甲试验田小麦长势比较整齐.
故答案为:甲.
8. ,
【解析】设一组数据的平均数为,
∵极差为a,方差为s2,
∴极差=xn+2 (x1+2)=xn x1=a,
原来的方差s2=[(x1 )2+(x2 )2+…+(xn )2],
现在的方差S2=[(x1+a a)2+(x2 a a)2+…+(xn+a a)2]=s2;
故答案为a;s2
9.2
【解析】由题意知,原数据的平均数为,新数据的每一个数都加了1,则平均数变为+1,
则原来的方差S12=[(x1-)2+(x2-)2+…+(x5-)2]=2,
现在的方差S22=[(x1+1--1)2+(x2+1--1)2+…+(x5+1--1)2]=[(x1-)2+(x2-)2+…+(x5-)2]=2,
所以方差不变.
故答案为:2.
10.9
【解析】共有6个数据,排序后1总在中间,中位数应该是排序后的第3个和第4个数的平均数,则有,
∴x=1,
∴这组数据的平均数=,
∴方差==9,
故答案为:9.
11. ;标准差.
【解析】解:∵方差公式:S2= [(x1-)2+(x2-)2+…+(xn-)2]
∴S= ,把它叫做这组数据的标准差,它是衡量一组数据的波动大小的重要的量.
故答案为(1). (2). 标准差
12.小明 小明的成绩更稳定
【解析】解:由折线统计图可以看出,小华和小明的平均成绩相同,都是7.5,但小明的成绩比较稳定.
故答案为:小明;小明的成绩更稳定.
13.选购甲加工厂生产的鸡腿.
【解析】检查人员从甲、乙两家农副产品加工厂各随机抽取的15个鸡腿分别组成一个样本,样本数据的平均数分别是
,
.
样本数据的方差分别是
,
.
由可知,两家加工厂的鸡腿质量大致相等;由可知,甲加工厂的鸡腿质量更稳定,大小更均匀.因此,快餐公司应该选购甲加工厂生产的鸡腿.
14.从平均成绩看,甲和乙的成绩比较好;从方差看,乙和丙发挥都比甲稳定,但结合平均成绩看,乙的水平更高
【解析】本题力图进一步突出解决统计问题时可以“先直观估计再理性计算”.
图中反映甲、乙成绩的折线基本位于丙的上方,因此甲、乙的平均成绩高于丙;从图形看波动(离散程度),很明显乙和丙的数据波动较小,从平均成绩看,甲和乙的成绩比较好;从方差看,乙和丙发挥都比甲稳定,但结合平均成绩看,乙的水平更高.
15.可以要求退货
【解析】解:由题意得, 这20个螺丝的直径平均值为:×(11.8+11.7+12.0+12.1+12.3+12.2+12.0,11.5+···+11.8+11.9)=12(mm)
S2==0.048
∴S0.22(mm)>0.2(mm)
∴可以退货.
16.甲、乙两支仪仗队队员身高的平均数都是178cm,极差分别是2cm和4cm,方差分别是0.6和1.8,因此可以认为,甲仪仗队更为整齐
【解析】解:,
;
,;
,
;
∴甲、乙两支仪仗队队员身高的平均数都是178cm,
极差分别是2cm和4cm,方差分别是0.6和1.8,
因此可以认为,甲仪仗队更为整齐.
17.(1)9.5,10;(2)平均成绩9分,方差1;(3)乙
【解析】解:(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:×(10×4+8×2+7+9×3)=9,
则方差是:×[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;
(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队;
故答案为:乙.
18.(1)a=5,b=1;(2)m=6;n=20%;(3)八年级队比七年级队成绩好,理由见解析.
【解析】解:(1)根据题意得:,
解得a=5,b=1;
(2)七年级成绩为3,6,6,6,6,6,7,8,9,10,中位数为6,即m=6;
优秀率为=20%,即n=20%;
(3)八年级平均分高于七年级,方差小于七年级,成绩比较稳定,
故八年级队比七年级队成绩好.答案第1页,共2页
答案第1页,共2页
20.2数据的波动程度-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若一组数据,0,2,4,的极差为7,则的值是( ).
A. B.6 C.7 D.6或
2.样本方差的计算公式S2=[(-30)2+(-30)]2+…+(-30)2]中,数字20和30分别表示样本中的( )
A.众数、中位数 B.方差、标准差
C.样本中数据的个数、平均数 D.样本中数据的个数、中位数
3.有一组数据7、11、12、7、7、8、11,下列说法错误的是( )
A.中位数是7 B.平均数是9 C.众数是7 D.极差为5
4.已知某运动队的甲、乙、丙、丁四名射击运动员平时训练的平均成绩(单位:环)以及方差(单位:环)如下表,现要选一名成绩优秀且稳定的队员参加某项比赛,则应选( )
甲 乙 丙 丁
9.0 9.0 9.5 9.5
0.5 2.2 1.7 0.5
A.甲 B.乙 C.丙 D.丁
5.如图所示,是小强同学根据某城区某天上午和下午各四个整时点的气温绘制成的折线统计图,根据统计图请回答:该天上午和下午气温比较稳定的是( )
A.上午 B.下午 C.上午与下午稳定情况相同 D.无法确定
6.如图是小明和小华射击成绩的统计图,两人都射击了10次,下列说法正确的是( )
A.小明成绩的方差比小华成绩的方差大 B.小明和小华成绩的众数相同
C.小明成绩的中位数比小华成绩的中位数大 D.小明和小华的平均成绩相同
二、填空题
7.随机从甲、乙两块试验田中各抽取株麦苗测量高度,计算平均数和方差的结果:,,,,则小麦长势比较整齐的试验田是_____________.
8.一组数据的极差为,方差为,则数据的极差为____,方差为___.
9.已知2,3,5,m,n五个数据的方差是2,那么3,4,6,m+1,n+1五个数据的方差是______.
10.已知一组数据-3,-2,1,3,6,x的中位数为1,则其方差为_________.
11.标准差:方差的算术平方根S=_________,叫做这组数据的 _________.
12.要从小华、小明两名射击运动员中选择一名运动员参加射击比赛,在赛前对他们进行了一次选拔赛,下图为小华、小明两人在选拔赛中各射击10次成绩的折线图和表示平均数的水平线.你认为应该选择______(填“小华”或“小明”)参加射击比赛;理由是__________.
三、解答题
13.某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如表所示.根据表中数据,你认为快餐公司应该选购哪家加工厂的鸡腿?
甲 74 74 75 74 76 73 76 73 76 75 78 77 74 72 73
乙 75 73 79 72 76 71 73 72 78 74 77 78 80 71 75
14.甲、乙、丙三人的射击成绩如图所示,三人中,谁射击成绩更好?谁更稳定?你是怎么判断的?
15.某商场新进了一批直径为12mm的螺丝,从中抽取了20个螺丝,并规定它们的标准差若大于0.2mm,就可要求退货,这20个螺丝的直径(单位:mm)如下:
11.8,11.7,12.0,12.1,12.3,12.2,12.0,11.5,12.3,12.1,
12.0,12.2,11.9,11.7,11.9,12.1,12.3,12.4,11.8,11.9
该商场是否可以要求退货?
16.甲、乙两支仪仗队队员的身高(单位:cm)如下:
甲队:178,177,179,179,178,178,177,178,177,179;
乙队:178,177,179,176,178,180,180,178,176,178.
哪支仪仗队队员的身高更为整齐?你是怎么判断的?
17.八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
18.我县某中学七、八年级各选派10名选手参加学校举办的“爱我太康”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别 平均分 中位数 方差 合格率 优秀率
七年级 6.7 m 3.41 90% n
八年级 7.1 7.5 1.69 80% 10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【解析】解:根据极差的计算法则可得:x-(-1)=7或4-x=7,
解得:x=6或x=-3.
故选D
2.C
【解析】解:∵S2=[(-30)2+(-30)]2+…+(-30)2]
∴20是样本中数据的个数,30是这组数据的平均数.
故选C.
3.A
【解析】这组数据按照从小到大的顺序排列为:7.7.7.8.11.11.12,
则中位数为8,平均数为,众数为7,极差为,
故选A.
4.D
【解析】解:
又
丁的成绩优秀且最稳定,
故选:D.
5.B
【解析】解: 上=(18+19+21+22)÷4=20,
下=(22.5+20+19+18.5)÷4=20,
S2上=[(18-20)2+(19-20)2+(21-20)2+(22-20)2]÷4=2.5,
S2下=[(22.5-20)2+(20-20)2+(19-20)2+(18.5-20)2]÷4=2.375,
∵S2上>S2下,
∴下午的气温更稳定.
故选B.
6.D
【解析】解:小华成绩是:8,7,3,8,3,10,6,10,8,8,从小到大排序为3,3,6,7,8,8,8,8,10,10,
中位数是8,众数是8,平均数,
方差
小明成绩是8,9,8,8,7,8,7,6,7,8,从小到大排序为6,7,7,7,8,8,8,8,8,9,
中位数是8,众数是8,平均数,
方差
A.根据折线统计图可知,小明的成绩波动较小,小华成绩的波动较大,故小明的成绩的方差较小;故选项A不正确;
B.小明和小华的成绩中,8环出现的次数均最多,故众数都是8环;故选项B正确;
C.将小明和小华的成绩分别按大小顺序排列,每组数据的中间两个数都是8,故中位数都是8环;故选项C不正确;
D.小明的平均成绩为7.6环,小华的平均成绩为7.1环,故选项D不正确.
故选D.
7.甲
【解析】解:由方差的意义,观察数据可知,
∵,
∴甲块试验田的方差小,
故甲试验田小麦长势比较整齐.
故答案为:甲.
8. ,
【解析】设一组数据的平均数为,
∵极差为a,方差为s2,
∴极差=xn+2 (x1+2)=xn x1=a,
原来的方差s2=[(x1 )2+(x2 )2+…+(xn )2],
现在的方差S2=[(x1+a a)2+(x2 a a)2+…+(xn+a a)2]=s2;
故答案为a;s2
9.2
【解析】由题意知,原数据的平均数为,新数据的每一个数都加了1,则平均数变为+1,
则原来的方差S12=[(x1-)2+(x2-)2+…+(x5-)2]=2,
现在的方差S22=[(x1+1--1)2+(x2+1--1)2+…+(x5+1--1)2]=[(x1-)2+(x2-)2+…+(x5-)2]=2,
所以方差不变.
故答案为:2.
10.9
【解析】共有6个数据,排序后1总在中间,中位数应该是排序后的第3个和第4个数的平均数,则有,
∴x=1,
∴这组数据的平均数=,
∴方差==9,
故答案为:9.
11. ;标准差.
【解析】解:∵方差公式:S2= [(x1-)2+(x2-)2+…+(xn-)2]
∴S= ,把它叫做这组数据的标准差,它是衡量一组数据的波动大小的重要的量.
故答案为(1). (2). 标准差
12.小明 小明的成绩更稳定
【解析】解:由折线统计图可以看出,小华和小明的平均成绩相同,都是7.5,但小明的成绩比较稳定.
故答案为:小明;小明的成绩更稳定.
13.选购甲加工厂生产的鸡腿.
【解析】检查人员从甲、乙两家农副产品加工厂各随机抽取的15个鸡腿分别组成一个样本,样本数据的平均数分别是
,
.
样本数据的方差分别是
,
.
由可知,两家加工厂的鸡腿质量大致相等;由可知,甲加工厂的鸡腿质量更稳定,大小更均匀.因此,快餐公司应该选购甲加工厂生产的鸡腿.
14.从平均成绩看,甲和乙的成绩比较好;从方差看,乙和丙发挥都比甲稳定,但结合平均成绩看,乙的水平更高
【解析】本题力图进一步突出解决统计问题时可以“先直观估计再理性计算”.
图中反映甲、乙成绩的折线基本位于丙的上方,因此甲、乙的平均成绩高于丙;从图形看波动(离散程度),很明显乙和丙的数据波动较小,从平均成绩看,甲和乙的成绩比较好;从方差看,乙和丙发挥都比甲稳定,但结合平均成绩看,乙的水平更高.
15.可以要求退货
【解析】解:由题意得, 这20个螺丝的直径平均值为:×(11.8+11.7+12.0+12.1+12.3+12.2+12.0,11.5+···+11.8+11.9)=12(mm)
S2==0.048
∴S0.22(mm)>0.2(mm)
∴可以退货.
16.甲、乙两支仪仗队队员身高的平均数都是178cm,极差分别是2cm和4cm,方差分别是0.6和1.8,因此可以认为,甲仪仗队更为整齐
【解析】解:,
;
,;
,
;
∴甲、乙两支仪仗队队员身高的平均数都是178cm,
极差分别是2cm和4cm,方差分别是0.6和1.8,
因此可以认为,甲仪仗队更为整齐.
17.(1)9.5,10;(2)平均成绩9分,方差1;(3)乙
【解析】解:(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:×(10×4+8×2+7+9×3)=9,
则方差是:×[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;
(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队;
故答案为:乙.
18.(1)a=5,b=1;(2)m=6;n=20%;(3)八年级队比七年级队成绩好,理由见解析.
【解析】解:(1)根据题意得:,
解得a=5,b=1;
(2)七年级成绩为3,6,6,6,6,6,7,8,9,10,中位数为6,即m=6;
优秀率为=20%,即n=20%;
(3)八年级平均分高于七年级,方差小于七年级,成绩比较稳定,
故八年级队比七年级队成绩好.答案第1页,共2页
答案第1页,共2页
