2021-2022年初中数学八年级下册同步(人教版)20.3课题学习体质健康测试中的数据分析 课堂练习(word版含答案)
文档属性
| 名称 | 2021-2022年初中数学八年级下册同步(人教版)20.3课题学习体质健康测试中的数据分析 课堂练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 320.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 09:47:21 | ||
图片预览




文档简介
2021-2022年初中数学八年级下册同步(人教版)
20.3课题学习 体质健康测试中的数据分析-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为( )
A.4,5 B.5,4 C.4,4 D.5,5
2.某“中学生暑期环保小组”的同学,随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,8,10,5,9.利用上述数据估计该小区2000户家庭一周内需要环保方便袋约( )
A.2000只 B.14000只 C.21000只 D.98000只
3.为了解某地区初一年级名学生的体重情况,现从中抽测了名学生的体重,就这个问题来说,下面的说法中正确的是( )
A.名学生是总体 B.每个学生是个体
C.名学生是所抽取的一个样本 D.样本容量是
4.依据国家实行的《国家学生体质健康标准》,对怀柔区初一学生身高进行抽样调查,以便总结怀柔区初一学生现存的身高问题,分析其影响因素,为学生的健康发展及学校体育教育改革提出合理项建议.已知怀柔区初一学生有男生840人,女生800人,他们的身高在 范围内,随机抽取初一学生进行抽样调查.抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表;
根据统计图表提供的信息,下列说法中
①抽取男生的样本中,身高 之间的学生有18人;
②初一学生中女生的身高的中位数在组;
③抽取的样本中抽取女生的样本容量是38;
④初一学生身高在 之间的学生约有800人.其中合理的是( )
A.①② B.①④ C.②④ D.③④
5.某县举办老、中、青三个年龄段五公里竞走活动,其人数比为,如图所示的扇形统计图表示 上述分布情况,已知老人有人,则下列说法不正确的是( )
A.老年所占区域的圆心角是 B.参加活动的总人数是人
C.中年人比老年人多 D.老年人比青年人少人
6.在2019年南充市初中毕业升学体育与健康考试中,某校九年级(1)班体育委员对本班50名同学参加球类自选项目做了统计,制作出扇形统计图(如图),则该班选考乒乓球人数比羽毛球人数多( )
A.5人 B.10人 C.15人 D.20人
二、填空题
7.一组数据1,3,2,5,2,a的众数是a,这组数据的中位数是_______.
8.为迎接五月份全县中考九年级体育测试,小强每天坚持引体向上锻炼,他记录了某周每天做引体向上的个数,如下表.
星期 日 一 二 三 四 五 六
个数 11 12 13 12
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据的唯一众数是13,平均数是12,那么这组数据的方差是________.
9.在一次爱心捐款中,某班有40名学生拿出自己的零花钱,有捐5元、10元、20元、50元的.如图所示的是不同捐款的人数比例,那么这个班的学生平均每人捐款_________元,中位数是_________元,众数是_________元.
10.我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图,则这10个样本数据的平均数是___,众数是___,中位数是___.
11.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s2:
甲 乙 丙 丁
平均数(cm) 561 560 561 560
方差s2(cm2) 3.5 3.5 15.5 16.5
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择_____.
12.如图,是甲、乙两地5月上旬的日平均气温统计图,则甲、乙两地这6天日平均气温的方差大小关系为:______(填“<”或“>”号),甲、乙两地气温更稳定的是:______.
三、解答题
13.某校为了解初中学生每天在校体育活动的时间(单位:h),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的初中学生人数为___________,图①中m的值为_____________;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数.
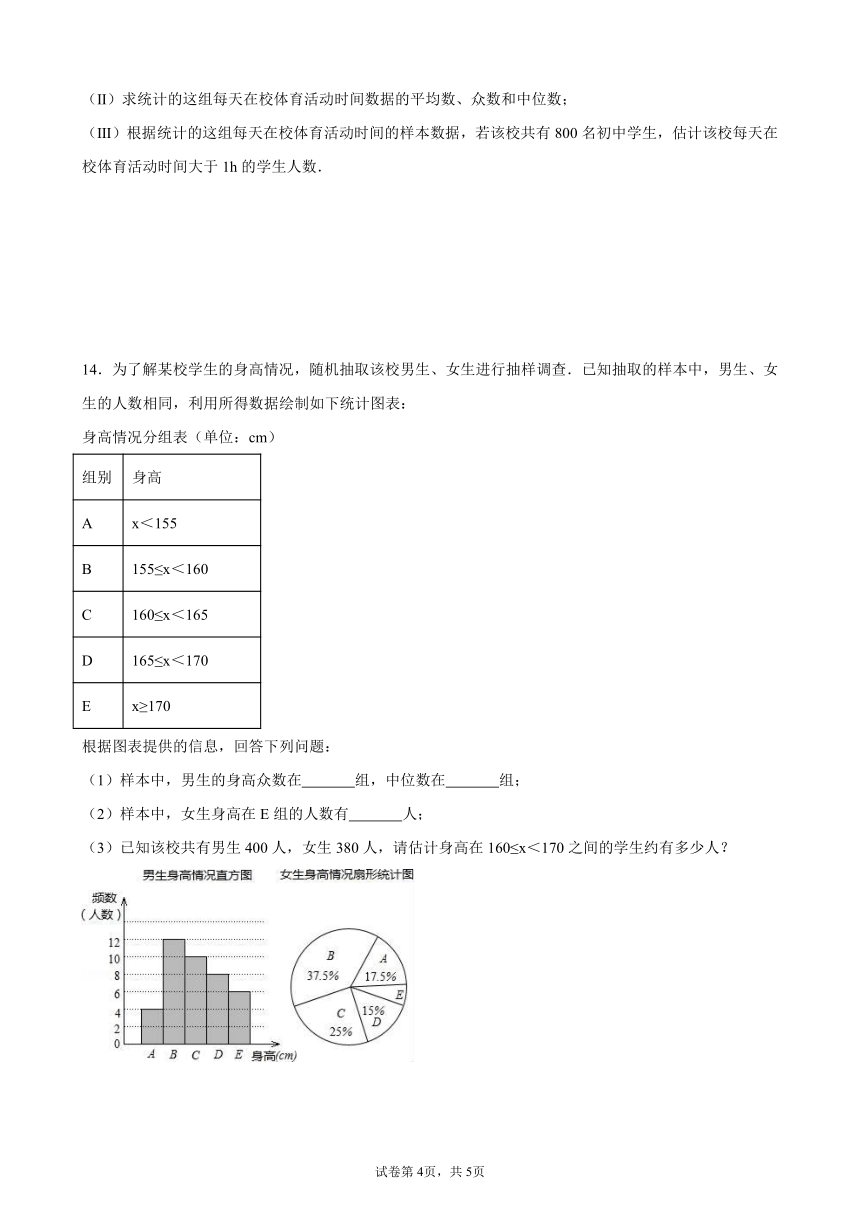
14.为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 身高
A x<155
B 155≤x<160
C 160≤x<165
D 165≤x<170
E x≥170
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组;
(2)样本中,女生身高在E组的人数有 人;
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?
15.某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
16.北京和南京两城市月降水量统计表(单位:0.1 mm)
月份 城市 1月 2月 3月 4月 5月 6月 7月 8月 9月 10月 11月
北 京 26 59 90 264 287 707 1 756 1 822 487 188 60
南 京 288 481 688 866 964 1 592 1 875 1 237 951 599 556
根据上表,回答下列问题:
(1)哪一个城市一年的降水量大?哪一个城市一年的降水量变化幅度大?
(2)两个城市在哪个月的降水量相差最大?差多少?
(3)哪几个月两城市的降水量相差在30 mm以内.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【解析】解:将数据从小到大排列为:1,2,3,3,4,4,5,5,5,5,这组数据的众数为:5;中位数为:4
故选:A.
2.B
【解析】(6+5+7+8+7+5+8+10+5+9)×2000=14000只.
故选B.
3.D
【解析】解:总体为“某地区初一年级9000名学生的体重情况”因此A不正确,个体为“每个学生的体重情况”故B不正确,样本为“抽测了600名学生的体重”因此C不正确,样本容量为“从总体中抽取个体的数量”因此D正确,
故选D.
4.B
【解析】解:由直方图可知,抽取男生的样本中,身高在155≤x<165之间的学生有8+10=18人,故①正确;
由A与B的百分比之和为10.5%+37.5%=48%<50%,则女生身高的中位数在C组,故②错误;
∵男生身高的样本容量为4+8+10+12+8=42,
∴女生身高的样本容量为40,故③错误;
∵女生身高在160cm至170cm(不含170cm)的学生有40×(30%+15%)=18人,
∴身高在160cm至170cm(不含170cm)的学生有(840+800)×=800(人),故④正确;
故选B.
5.D
【解析】解:A、老年的人数是总人数的,老年所占区域的圆心角是,故此选项正确,不符合题意;
B、参加活动的总人数是,故此选项正确,不符合题意;
C、中年人数是,老年人数是160,中年人比老年人多80,故此选项正确,不符合题意;
D、青年人数是,老年人比青年人少400-160=240人,故此选项错误,符合题意.
故选D.
6.B
【解析】解:∵选考乒乓球人数为50×40%=20人,
选考羽毛球人数为人,
∴选考乒乓球人数比羽毛球人数多20-10=10人,
故选B.
7.2.
【解析】由于众数是出现次数最多的,因此知a=1或2、3、5,当a=2时,把数据排列为1、2、2、2、3、5,且共6个数据,因此中位数为;当a=1时,把数据排列为1、1、2、2、3、5,且共6个数据,因此中位数为;当a=3时,把数据排列为1、2、2、3、3、5,且共6个数据,因此中位数为;当a=5时,把数据排列为1、2、2、3、5、5,且共6个数据,因此中位数为.因此中位数为2或2.5.
8.
【解析】平均数是12,
这组数据的和为,
被墨汁覆盖的数的和为.
这组数据的唯一众数是13,
被墨汁覆盖的三个数为10,13,13,
∴.
故答案为:.
9.16 , 5 , 5 .
【解析】这个班的学生捐款的平均数是:5×60%+10×10%+20×10%+50×20%=16(元);
捐5元、10元、20元、50元的人数分别是:40×60%=24,40×10%=4,40×10%=4,40×20%=8,
把40名同学捐款从小到大排列,最中间的两个数是5,5,所以中位数是(5+5)÷2=5(元);
由于捐款5元的有24人,人数最多,所以众数是5元,
答:这个班的学生捐款的平均数、中位数、众数分别是16元、5元、5元.
10.6.8 6.5 6.5
【解析】观察条形图,可知这组样本数据的平均数是: =6.8,
即这组样本数据的平均数为6.8(t).
在这组样本数据中,6.5出现了4次,出现的次数最多,
这组数据的众数是6.5(t).
将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是6.5,
有6.5+6.52=6.5,
即这组数据的中位数是6.5(t).
故答案为6.8,6.5,6.5.
11.甲
【解析】∵ ,
∴从甲和丙中选择一人参加比赛,
∵ ,
∴选择甲参赛,
故答案为甲.
12.> 乙
【解析】观察平均气温统计图可知:乙地的平均气温比较稳定,波动小;
故乙地的日平均气温的方差小.
故S2甲>S2乙.
故答案是:>,乙.
13.(Ⅰ)40,25;(Ⅱ)平均数是1.5,众数为1.5,中位数为1.5;(Ⅲ)每天在校体育活动时间大于1h的学生人数约为720.
【解析】解:(Ⅰ)本次接受调查的初中学生人数为:4+8+15+10+3=40(人),
m=100×=25.
故答案是:40,25;
(Ⅱ)观察条形统计图,
∵,
∴这组数据的平均数是1.5.
∵在这组数据中,1.5出现了15次,出现的次数最多,
∴这组数据的众数为1.5.
∵将这组数据按从小到大的顺序棑列,其中处于中间的两个数都是1.5,有,
∴这组数据的中位数为1.5.
(Ⅲ)∵在统计的这组每天在校体育活动时间的样本数据中,每天在校体育活动时间大于1h的学生人数占90%,
∴估计该校800名初中学生中,每天在校体育活动时间大于1h的人数约占90%.有.
∴该校800名初中学生中,每天在校体育活动时间大于1h的学生人数约为720.
14.(1)B、C;(2)2;(3)332人
【解析】解:∵B组人数最多,
∴众数在B组,
男生总人数为4+12+10+8+6=40,
按照从低到高的顺序,第20、21两人都在C组,
∴中位数在C组,
故答案为B、C;
(2)女生身高在E组的频率为:1﹣17.5%﹣37.5%﹣25%﹣15%=5%,
∵抽取的样本中,男生、女生的人数相同,
∴样本中,女生身高在E组的人数有40×5%=2人,
故答案为2;
(3)400×+380×(25%+15%)=180+152=332(人).
答:估计该校身高在160≤x<170之间的学生约有332人.
15.(1)样本容量为50;(2)平均数为14(岁);中位数为14(岁),众数为15岁;(3)估计该校年龄在15岁及以上的学生人数为720人.
【解析】解:(1)样本容量为6÷12%=50;
(2)14岁的人数为50×28%=14、16岁的人数为50﹣(6+10+14+18)=2,
则这组数据的平均数为=14(岁),
中位数为=14(岁),众数为15岁;
(3)估计该校年龄在15岁及以上的学生人数为1800×=720人.
16.(1) 南京一年的降水量大;北京一年的降水量变化幅度大. (2) 6月份;88.5mm(3)1月、7月
【解析】解:(1)北京一年的降水量为579.9 mm,南京一年的降水量为1 041. 9 mm,所以南京一年的降水量大.北京降水量的波动范围从2.6 mm到182.2 mm.南京降水量的波动范围从28.8 mm到187.5 mm,因此北京一年的降水量变化幅度大.
(2)比较每个月两个城市降水量差,可得6月份两个城市的降水量相差最大,
为159.2—70.7=88.5(mm).
(3)其中1月、7月两城市的降水量相差在30 mm以内.答案第1页,共2页
答案第1页,共2页
20.3课题学习 体质健康测试中的数据分析-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为( )
A.4,5 B.5,4 C.4,4 D.5,5
2.某“中学生暑期环保小组”的同学,随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,8,10,5,9.利用上述数据估计该小区2000户家庭一周内需要环保方便袋约( )
A.2000只 B.14000只 C.21000只 D.98000只
3.为了解某地区初一年级名学生的体重情况,现从中抽测了名学生的体重,就这个问题来说,下面的说法中正确的是( )
A.名学生是总体 B.每个学生是个体
C.名学生是所抽取的一个样本 D.样本容量是
4.依据国家实行的《国家学生体质健康标准》,对怀柔区初一学生身高进行抽样调查,以便总结怀柔区初一学生现存的身高问题,分析其影响因素,为学生的健康发展及学校体育教育改革提出合理项建议.已知怀柔区初一学生有男生840人,女生800人,他们的身高在 范围内,随机抽取初一学生进行抽样调查.抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表;
根据统计图表提供的信息,下列说法中
①抽取男生的样本中,身高 之间的学生有18人;
②初一学生中女生的身高的中位数在组;
③抽取的样本中抽取女生的样本容量是38;
④初一学生身高在 之间的学生约有800人.其中合理的是( )
A.①② B.①④ C.②④ D.③④
5.某县举办老、中、青三个年龄段五公里竞走活动,其人数比为,如图所示的扇形统计图表示 上述分布情况,已知老人有人,则下列说法不正确的是( )
A.老年所占区域的圆心角是 B.参加活动的总人数是人
C.中年人比老年人多 D.老年人比青年人少人
6.在2019年南充市初中毕业升学体育与健康考试中,某校九年级(1)班体育委员对本班50名同学参加球类自选项目做了统计,制作出扇形统计图(如图),则该班选考乒乓球人数比羽毛球人数多( )
A.5人 B.10人 C.15人 D.20人
二、填空题
7.一组数据1,3,2,5,2,a的众数是a,这组数据的中位数是_______.
8.为迎接五月份全县中考九年级体育测试,小强每天坚持引体向上锻炼,他记录了某周每天做引体向上的个数,如下表.
星期 日 一 二 三 四 五 六
个数 11 12 13 12
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据的唯一众数是13,平均数是12,那么这组数据的方差是________.
9.在一次爱心捐款中,某班有40名学生拿出自己的零花钱,有捐5元、10元、20元、50元的.如图所示的是不同捐款的人数比例,那么这个班的学生平均每人捐款_________元,中位数是_________元,众数是_________元.
10.我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图,则这10个样本数据的平均数是___,众数是___,中位数是___.
11.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s2:
甲 乙 丙 丁
平均数(cm) 561 560 561 560
方差s2(cm2) 3.5 3.5 15.5 16.5
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择_____.
12.如图,是甲、乙两地5月上旬的日平均气温统计图,则甲、乙两地这6天日平均气温的方差大小关系为:______(填“<”或“>”号),甲、乙两地气温更稳定的是:______.
三、解答题
13.某校为了解初中学生每天在校体育活动的时间(单位:h),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的初中学生人数为___________,图①中m的值为_____________;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数.
14.为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 身高
A x<155
B 155≤x<160
C 160≤x<165
D 165≤x<170
E x≥170
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组;
(2)样本中,女生身高在E组的人数有 人;
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?
15.某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
16.北京和南京两城市月降水量统计表(单位:0.1 mm)
月份 城市 1月 2月 3月 4月 5月 6月 7月 8月 9月 10月 11月
北 京 26 59 90 264 287 707 1 756 1 822 487 188 60
南 京 288 481 688 866 964 1 592 1 875 1 237 951 599 556
根据上表,回答下列问题:
(1)哪一个城市一年的降水量大?哪一个城市一年的降水量变化幅度大?
(2)两个城市在哪个月的降水量相差最大?差多少?
(3)哪几个月两城市的降水量相差在30 mm以内.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【解析】解:将数据从小到大排列为:1,2,3,3,4,4,5,5,5,5,这组数据的众数为:5;中位数为:4
故选:A.
2.B
【解析】(6+5+7+8+7+5+8+10+5+9)×2000=14000只.
故选B.
3.D
【解析】解:总体为“某地区初一年级9000名学生的体重情况”因此A不正确,个体为“每个学生的体重情况”故B不正确,样本为“抽测了600名学生的体重”因此C不正确,样本容量为“从总体中抽取个体的数量”因此D正确,
故选D.
4.B
【解析】解:由直方图可知,抽取男生的样本中,身高在155≤x<165之间的学生有8+10=18人,故①正确;
由A与B的百分比之和为10.5%+37.5%=48%<50%,则女生身高的中位数在C组,故②错误;
∵男生身高的样本容量为4+8+10+12+8=42,
∴女生身高的样本容量为40,故③错误;
∵女生身高在160cm至170cm(不含170cm)的学生有40×(30%+15%)=18人,
∴身高在160cm至170cm(不含170cm)的学生有(840+800)×=800(人),故④正确;
故选B.
5.D
【解析】解:A、老年的人数是总人数的,老年所占区域的圆心角是,故此选项正确,不符合题意;
B、参加活动的总人数是,故此选项正确,不符合题意;
C、中年人数是,老年人数是160,中年人比老年人多80,故此选项正确,不符合题意;
D、青年人数是,老年人比青年人少400-160=240人,故此选项错误,符合题意.
故选D.
6.B
【解析】解:∵选考乒乓球人数为50×40%=20人,
选考羽毛球人数为人,
∴选考乒乓球人数比羽毛球人数多20-10=10人,
故选B.
7.2.
【解析】由于众数是出现次数最多的,因此知a=1或2、3、5,当a=2时,把数据排列为1、2、2、2、3、5,且共6个数据,因此中位数为;当a=1时,把数据排列为1、1、2、2、3、5,且共6个数据,因此中位数为;当a=3时,把数据排列为1、2、2、3、3、5,且共6个数据,因此中位数为;当a=5时,把数据排列为1、2、2、3、5、5,且共6个数据,因此中位数为.因此中位数为2或2.5.
8.
【解析】平均数是12,
这组数据的和为,
被墨汁覆盖的数的和为.
这组数据的唯一众数是13,
被墨汁覆盖的三个数为10,13,13,
∴.
故答案为:.
9.16 , 5 , 5 .
【解析】这个班的学生捐款的平均数是:5×60%+10×10%+20×10%+50×20%=16(元);
捐5元、10元、20元、50元的人数分别是:40×60%=24,40×10%=4,40×10%=4,40×20%=8,
把40名同学捐款从小到大排列,最中间的两个数是5,5,所以中位数是(5+5)÷2=5(元);
由于捐款5元的有24人,人数最多,所以众数是5元,
答:这个班的学生捐款的平均数、中位数、众数分别是16元、5元、5元.
10.6.8 6.5 6.5
【解析】观察条形图,可知这组样本数据的平均数是: =6.8,
即这组样本数据的平均数为6.8(t).
在这组样本数据中,6.5出现了4次,出现的次数最多,
这组数据的众数是6.5(t).
将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是6.5,
有6.5+6.52=6.5,
即这组数据的中位数是6.5(t).
故答案为6.8,6.5,6.5.
11.甲
【解析】∵ ,
∴从甲和丙中选择一人参加比赛,
∵ ,
∴选择甲参赛,
故答案为甲.
12.> 乙
【解析】观察平均气温统计图可知:乙地的平均气温比较稳定,波动小;
故乙地的日平均气温的方差小.
故S2甲>S2乙.
故答案是:>,乙.
13.(Ⅰ)40,25;(Ⅱ)平均数是1.5,众数为1.5,中位数为1.5;(Ⅲ)每天在校体育活动时间大于1h的学生人数约为720.
【解析】解:(Ⅰ)本次接受调查的初中学生人数为:4+8+15+10+3=40(人),
m=100×=25.
故答案是:40,25;
(Ⅱ)观察条形统计图,
∵,
∴这组数据的平均数是1.5.
∵在这组数据中,1.5出现了15次,出现的次数最多,
∴这组数据的众数为1.5.
∵将这组数据按从小到大的顺序棑列,其中处于中间的两个数都是1.5,有,
∴这组数据的中位数为1.5.
(Ⅲ)∵在统计的这组每天在校体育活动时间的样本数据中,每天在校体育活动时间大于1h的学生人数占90%,
∴估计该校800名初中学生中,每天在校体育活动时间大于1h的人数约占90%.有.
∴该校800名初中学生中,每天在校体育活动时间大于1h的学生人数约为720.
14.(1)B、C;(2)2;(3)332人
【解析】解:∵B组人数最多,
∴众数在B组,
男生总人数为4+12+10+8+6=40,
按照从低到高的顺序,第20、21两人都在C组,
∴中位数在C组,
故答案为B、C;
(2)女生身高在E组的频率为:1﹣17.5%﹣37.5%﹣25%﹣15%=5%,
∵抽取的样本中,男生、女生的人数相同,
∴样本中,女生身高在E组的人数有40×5%=2人,
故答案为2;
(3)400×+380×(25%+15%)=180+152=332(人).
答:估计该校身高在160≤x<170之间的学生约有332人.
15.(1)样本容量为50;(2)平均数为14(岁);中位数为14(岁),众数为15岁;(3)估计该校年龄在15岁及以上的学生人数为720人.
【解析】解:(1)样本容量为6÷12%=50;
(2)14岁的人数为50×28%=14、16岁的人数为50﹣(6+10+14+18)=2,
则这组数据的平均数为=14(岁),
中位数为=14(岁),众数为15岁;
(3)估计该校年龄在15岁及以上的学生人数为1800×=720人.
16.(1) 南京一年的降水量大;北京一年的降水量变化幅度大. (2) 6月份;88.5mm(3)1月、7月
【解析】解:(1)北京一年的降水量为579.9 mm,南京一年的降水量为1 041. 9 mm,所以南京一年的降水量大.北京降水量的波动范围从2.6 mm到182.2 mm.南京降水量的波动范围从28.8 mm到187.5 mm,因此北京一年的降水量变化幅度大.
(2)比较每个月两个城市降水量差,可得6月份两个城市的降水量相差最大,
为159.2—70.7=88.5(mm).
(3)其中1月、7月两城市的降水量相差在30 mm以内.答案第1页,共2页
答案第1页,共2页
