2021-2022年初中数学九年级下册同步(人教版)26.2实际问题与反比例函数 课堂练习(word版含解析)
文档属性
| 名称 | 2021-2022年初中数学九年级下册同步(人教版)26.2实际问题与反比例函数 课堂练习(word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 243.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 00:00:00 | ||
图片预览




文档简介
2021-2022年初中数学九年级下册同步(人教版)
26.2实际问题与反比例函数-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
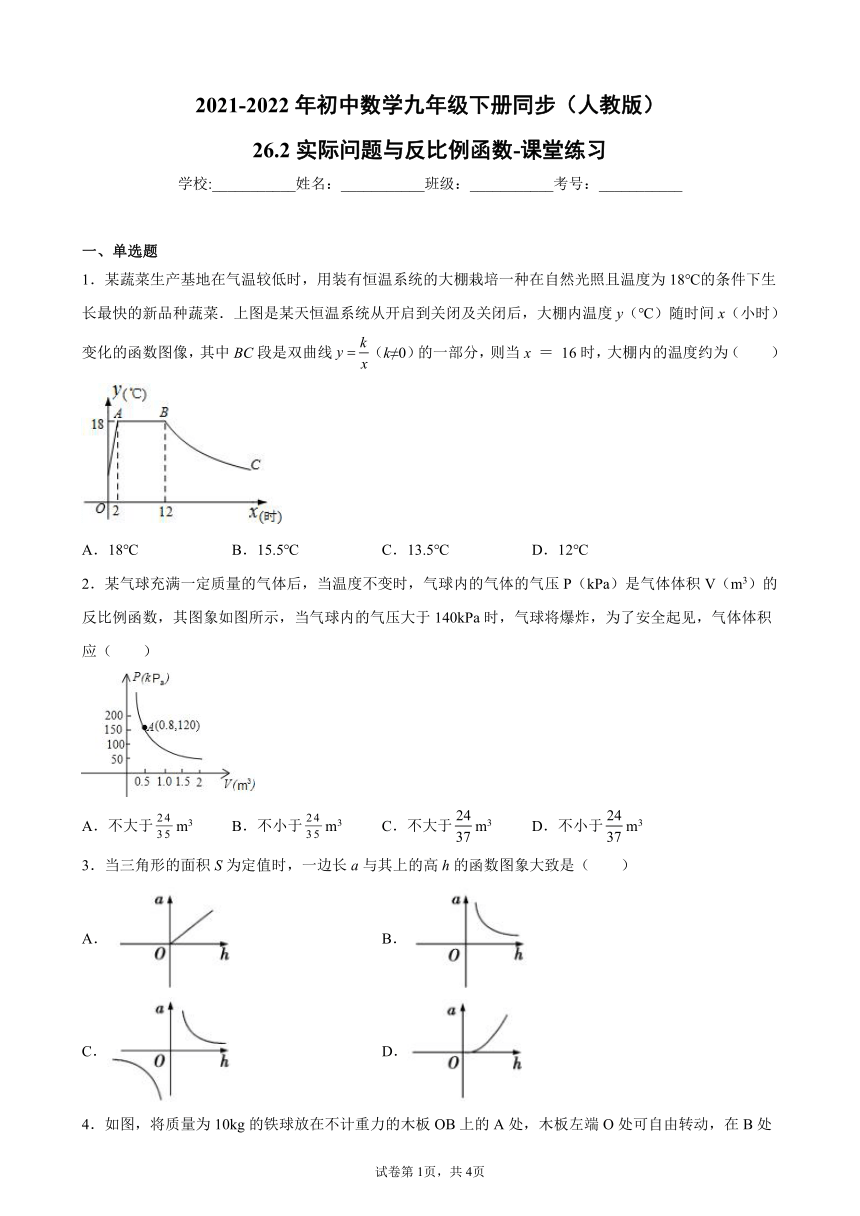
1.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种蔬菜.上图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图像,其中BC段是双曲线(k≠0)的一部分,则当x = 16时,大棚内的温度约为( )
A.18℃ B.15.5℃ C.13.5℃ D.12℃
2.某气球充满一定质量的气体后,当温度不变时,气球内的气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体体积应( )
A.不大于m3 B.不小于m3 C.不大于m3 D.不小于m3
3.当三角形的面积S为定值时,一边长a与其上的高h的函数图象大致是( )
A. B.
C. D.
4.如图,将质量为10kg的铁球放在不计重力的木板OB上的A处,木板左端O处可自由转动,在B处用力F竖直向上抬着木板,使其保持水平,已知OA的长为1m,OB的长为xm,g取10N/kg,则F关于x的函数解析式为( )
A. B. C. D.
5.某司机驾驶汽车从甲地去乙地,他以70千米/时的平均速度行驶了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(时)的函数解析式为( )
A. B. C. D.
6.今年某公司推出的一款新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买手机的活动,一部售价为9688元的新手机,前期付款3000元,后期每个月分别付相同的金额,则每个月付款金额y(元)与付款月数x(x为正整数)之间的函数关系式是( )
A. B. C. D.
二、填空题
7.已知经过闭合电路的电流I(单位:A)与电路的电阻R(单位:)是反比例函数关系,请填表格(结果保留小数点后两位):
A 1 2 3 4 5
20 25 30 50 65 80 90
8.在平整的路面上某型号汽车急刹车后仍将滑行的距离s(米)与刹车的速度v(千米/时)有这样的关系,当汽车紧急刹车仍滑行27米时,汽车刹车前的速度是____________千米/时.
9.在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2.y关于x的函数关系式是________,x的取值范围是________;
10.小明要把一篇28000字的社会调查报告录入电脑.完成录入的时间t(分)与录入文字的速度v(字/分)的函数关系式表示为________.
11.如图,一块长方体大理石板的、、三个面上的边长如图所示,如果大理石板的面向下放在地上时地面所受压强为帕,则把大理石板面向下放在地上时,地面所受压强是________帕.
12.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:y=(k≠0),其图象为如图的一段曲线,若这段公路行驶速度不得超过60km/h,则该汽车通过这段公路最少需要______h.
三、解答题
13.一司机驾驶汽车从甲地去乙地,他以的平均速度用到达目的地.
(1)当他按原路匀速返回时,汽车的速度v与时间t有怎样的函数关系?
(2)如果该司机必须在之内回到甲地,那么返程时的平均速度不能小于多少?
14.新建成的住宅楼主体工程已经竣工,只剩下楼体外表面需要贴瓷砖.已知楼体外表面的面积为.
(1)所需的瓷砖块数n与每块瓷砖的面积S(单位:)有怎样的函数关系?
(2)为了使住宅楼的外观更漂亮,建筑师决定采用灰、白和蓝三种颜色的瓷砖,每块瓷砖的面积都是,且灰、白、蓝瓷砖使用数量的比为,需要三种瓷砖各多少块?
15.某空调生产厂的装配车间计划在一段时期内组装9000台空调.
(1)在这段时期内,每天组装的数量m(台/天)与组装的时间t(天)之间有怎样的函数关系?
(2)原计划用2个月时间(每月按30天计算)完成这一任务,但由于气温提前升高,厂家决定这批空调提前10天完成组装,那么装配车间每天至少要组装多少台空调?比原计划多多少?
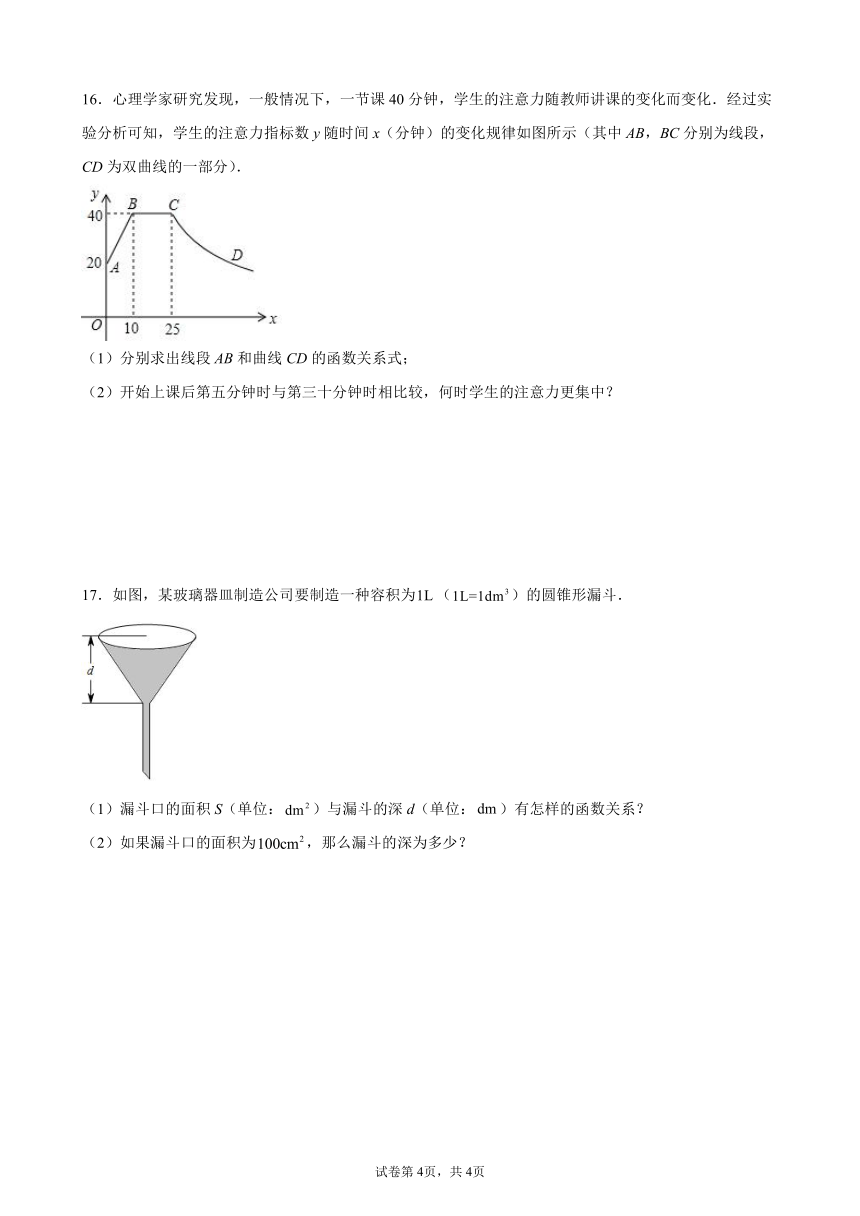
16.心理学家研究发现,一般情况下,一节课40分钟,学生的注意力随教师讲课的变化而变化.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,CD为双曲线的一部分).
(1)分别求出线段AB和曲线CD的函数关系式;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
17.如图,某玻璃器皿制造公司要制造一种容积为()的圆锥形漏斗.
(1)漏斗口的面积S(单位:)与漏斗的深d(单位:)有怎样的函数关系?
(2)如果漏斗口的面积为,那么漏斗的深为多少?
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:∵点B(12,18)在双曲线上,
∴,
解得:k=216.
当x=16时,y==13.5,
所以当x=16时,大棚内的温度约为13.5℃.
故选:C.
2.B
【解析】解:设球内气体的气压P(kPa)和气体体积V(m3)的关系式为P=,
∵图象过(0.8,120)
∴
∴P=,
∴当P≤140kPa时,V≥m3.
故选:B.
3.B
【解析】由题意可得,所以,所以a是h的反比例函数,因为,,所以其图象是双曲线在第一象限的部分.
故选B.
4.A
【解析】∵g取10N/kg,铁球质量为10kg,
∴G=mg=10×10=100(N),
∵OA=1m,OB=xm,
∴由杠杆平衡原理可得:F×OB=G×OA,即,
∴F关于x的函数解析式为.
故选A.
5.A
【解析】解:该司机以70千米/时的平均速度行驶了6小时到达目的地,
行驶的路程为(千米),
汽车的速度v(千米/时)与时间t(时)的函数解析式为:.
故选:A.
6.D
【解析】解:由题意得:,
即.
故选:D.
7.100;50;33.33;25;4;3.33;2;1.54;1.25;1.11.
【解析】解:依题意设I= ,
把I=5,R=20代入得:5=,
解得U=100,
所以I=.
当I=1,2,3,4,时,代入I=.分别取得R=100;50;33.33;25;
当R=25,30,50,65,80,90时,代入I=,分别求得I=4;3.33;2;1.54;1.25;1.11.
1 2 3 4 5 4 2
100 50 25 20 25 30 50 65 80 90
故答案为:100;50;33.33;25;4;3.33;2;1.54;1.25;1.11.
8.
【解析】依题意,,
,
解得:.
故答案为:.
9. x>0
【解析】解:∵在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2,
∴xy=2,
∴xy=4,
∴y关于x的函数关系式是y,
x的取值范围为x>0,
故答案为:y,x>0.
10.
【解析】由录入的时间=录入总量÷录入速度,
可得:,
故答案为:.
11.3.
【解析】设大理石板重力为F,
则P S=F,
,F=3×6 m.
∵当B面朝下时S=1×6,
∴帕.
故答案为3.
12.
【解析】解:由题意可得:k=xy=40,
则y≥=,
即该汽车通过这段公路最少需要h.
故答案为.
13.(1);(2)
【解析】解:(1)由题意得,两地路程为80×6=480(km),
故汽车的速度v与时间t的函数关系为:v=.
(2)由v=,得t=,
又由题知:t≤4,
∴≤4.
∵v>0
∴480≤4v.
∴v≥120.
答:返程时的平均速度不能低于120 km/h.
14.(1);(2)250000块,250000块,125000块
【解析】解:(1)∵每块瓷砖的面积Sm2=楼体外表的总面积÷所需的瓷砖块数m块,
由此可得出S与n的函数关系式是:S= ;
(2)当S=80×10-4=8×10-3 m2时,
n==625000,
设用灰瓷砖2x块,则白瓷砖、蓝瓷砖分别为2x块、x块,
依据题意得出:x+2x+2x=625000,
解得:x=125000,
∴需要灰瓷砖250000块,白瓷砖250000块、蓝瓷砖为125000块.
15.(1);(2)180台,30台
【解析】解:(1)每天组装的台数(单位:台天)与生产时间(单位:天)之间的函数关系:;
(2)当时,.
所以,这批空调提前10天上市,那么原装配车间每天至少要组装180台空调,
原计划用2个月时间(每月按30天计算)完成这一任务,则每天组装150台,
即比原计划多:台.
16.(1),;(2)第30分钟时注意力更集中
【解析】解:(1)设线段AB所在直线的解析式为,
把点代入,得,
∴;
设C、D所在双曲线的解析式为,
把点代入,得,
∴;
(2)当时,,
当时,,
∴,
∴第30分钟时注意力更集中.
17.(1);(2)
【解析】解:(1)根据圆锥体积=×底面积×高,得,
则,
故漏斗口的面积S与漏斗的深度d之间的函数关系为:;
(2)∵S=100cm2=1dm2,
∴,
解得d=3dm=30cm,
故漏斗口的面积为100cm2,那么漏斗的深为30cm.
答案第1页,共2页
答案第1页,共2页
26.2实际问题与反比例函数-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种蔬菜.上图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图像,其中BC段是双曲线(k≠0)的一部分,则当x = 16时,大棚内的温度约为( )
A.18℃ B.15.5℃ C.13.5℃ D.12℃
2.某气球充满一定质量的气体后,当温度不变时,气球内的气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体体积应( )
A.不大于m3 B.不小于m3 C.不大于m3 D.不小于m3
3.当三角形的面积S为定值时,一边长a与其上的高h的函数图象大致是( )
A. B.
C. D.
4.如图,将质量为10kg的铁球放在不计重力的木板OB上的A处,木板左端O处可自由转动,在B处用力F竖直向上抬着木板,使其保持水平,已知OA的长为1m,OB的长为xm,g取10N/kg,则F关于x的函数解析式为( )
A. B. C. D.
5.某司机驾驶汽车从甲地去乙地,他以70千米/时的平均速度行驶了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(时)的函数解析式为( )
A. B. C. D.
6.今年某公司推出的一款新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买手机的活动,一部售价为9688元的新手机,前期付款3000元,后期每个月分别付相同的金额,则每个月付款金额y(元)与付款月数x(x为正整数)之间的函数关系式是( )
A. B. C. D.
二、填空题
7.已知经过闭合电路的电流I(单位:A)与电路的电阻R(单位:)是反比例函数关系,请填表格(结果保留小数点后两位):
A 1 2 3 4 5
20 25 30 50 65 80 90
8.在平整的路面上某型号汽车急刹车后仍将滑行的距离s(米)与刹车的速度v(千米/时)有这样的关系,当汽车紧急刹车仍滑行27米时,汽车刹车前的速度是____________千米/时.
9.在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2.y关于x的函数关系式是________,x的取值范围是________;
10.小明要把一篇28000字的社会调查报告录入电脑.完成录入的时间t(分)与录入文字的速度v(字/分)的函数关系式表示为________.
11.如图,一块长方体大理石板的、、三个面上的边长如图所示,如果大理石板的面向下放在地上时地面所受压强为帕,则把大理石板面向下放在地上时,地面所受压强是________帕.
12.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:y=(k≠0),其图象为如图的一段曲线,若这段公路行驶速度不得超过60km/h,则该汽车通过这段公路最少需要______h.
三、解答题
13.一司机驾驶汽车从甲地去乙地,他以的平均速度用到达目的地.
(1)当他按原路匀速返回时,汽车的速度v与时间t有怎样的函数关系?
(2)如果该司机必须在之内回到甲地,那么返程时的平均速度不能小于多少?
14.新建成的住宅楼主体工程已经竣工,只剩下楼体外表面需要贴瓷砖.已知楼体外表面的面积为.
(1)所需的瓷砖块数n与每块瓷砖的面积S(单位:)有怎样的函数关系?
(2)为了使住宅楼的外观更漂亮,建筑师决定采用灰、白和蓝三种颜色的瓷砖,每块瓷砖的面积都是,且灰、白、蓝瓷砖使用数量的比为,需要三种瓷砖各多少块?
15.某空调生产厂的装配车间计划在一段时期内组装9000台空调.
(1)在这段时期内,每天组装的数量m(台/天)与组装的时间t(天)之间有怎样的函数关系?
(2)原计划用2个月时间(每月按30天计算)完成这一任务,但由于气温提前升高,厂家决定这批空调提前10天完成组装,那么装配车间每天至少要组装多少台空调?比原计划多多少?
16.心理学家研究发现,一般情况下,一节课40分钟,学生的注意力随教师讲课的变化而变化.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,CD为双曲线的一部分).
(1)分别求出线段AB和曲线CD的函数关系式;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
17.如图,某玻璃器皿制造公司要制造一种容积为()的圆锥形漏斗.
(1)漏斗口的面积S(单位:)与漏斗的深d(单位:)有怎样的函数关系?
(2)如果漏斗口的面积为,那么漏斗的深为多少?
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:∵点B(12,18)在双曲线上,
∴,
解得:k=216.
当x=16时,y==13.5,
所以当x=16时,大棚内的温度约为13.5℃.
故选:C.
2.B
【解析】解:设球内气体的气压P(kPa)和气体体积V(m3)的关系式为P=,
∵图象过(0.8,120)
∴
∴P=,
∴当P≤140kPa时,V≥m3.
故选:B.
3.B
【解析】由题意可得,所以,所以a是h的反比例函数,因为,,所以其图象是双曲线在第一象限的部分.
故选B.
4.A
【解析】∵g取10N/kg,铁球质量为10kg,
∴G=mg=10×10=100(N),
∵OA=1m,OB=xm,
∴由杠杆平衡原理可得:F×OB=G×OA,即,
∴F关于x的函数解析式为.
故选A.
5.A
【解析】解:该司机以70千米/时的平均速度行驶了6小时到达目的地,
行驶的路程为(千米),
汽车的速度v(千米/时)与时间t(时)的函数解析式为:.
故选:A.
6.D
【解析】解:由题意得:,
即.
故选:D.
7.100;50;33.33;25;4;3.33;2;1.54;1.25;1.11.
【解析】解:依题意设I= ,
把I=5,R=20代入得:5=,
解得U=100,
所以I=.
当I=1,2,3,4,时,代入I=.分别取得R=100;50;33.33;25;
当R=25,30,50,65,80,90时,代入I=,分别求得I=4;3.33;2;1.54;1.25;1.11.
1 2 3 4 5 4 2
100 50 25 20 25 30 50 65 80 90
故答案为:100;50;33.33;25;4;3.33;2;1.54;1.25;1.11.
8.
【解析】依题意,,
,
解得:.
故答案为:.
9. x>0
【解析】解:∵在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2,
∴xy=2,
∴xy=4,
∴y关于x的函数关系式是y,
x的取值范围为x>0,
故答案为:y,x>0.
10.
【解析】由录入的时间=录入总量÷录入速度,
可得:,
故答案为:.
11.3.
【解析】设大理石板重力为F,
则P S=F,
,F=3×6 m.
∵当B面朝下时S=1×6,
∴帕.
故答案为3.
12.
【解析】解:由题意可得:k=xy=40,
则y≥=,
即该汽车通过这段公路最少需要h.
故答案为.
13.(1);(2)
【解析】解:(1)由题意得,两地路程为80×6=480(km),
故汽车的速度v与时间t的函数关系为:v=.
(2)由v=,得t=,
又由题知:t≤4,
∴≤4.
∵v>0
∴480≤4v.
∴v≥120.
答:返程时的平均速度不能低于120 km/h.
14.(1);(2)250000块,250000块,125000块
【解析】解:(1)∵每块瓷砖的面积Sm2=楼体外表的总面积÷所需的瓷砖块数m块,
由此可得出S与n的函数关系式是:S= ;
(2)当S=80×10-4=8×10-3 m2时,
n==625000,
设用灰瓷砖2x块,则白瓷砖、蓝瓷砖分别为2x块、x块,
依据题意得出:x+2x+2x=625000,
解得:x=125000,
∴需要灰瓷砖250000块,白瓷砖250000块、蓝瓷砖为125000块.
15.(1);(2)180台,30台
【解析】解:(1)每天组装的台数(单位:台天)与生产时间(单位:天)之间的函数关系:;
(2)当时,.
所以,这批空调提前10天上市,那么原装配车间每天至少要组装180台空调,
原计划用2个月时间(每月按30天计算)完成这一任务,则每天组装150台,
即比原计划多:台.
16.(1),;(2)第30分钟时注意力更集中
【解析】解:(1)设线段AB所在直线的解析式为,
把点代入,得,
∴;
设C、D所在双曲线的解析式为,
把点代入,得,
∴;
(2)当时,,
当时,,
∴,
∴第30分钟时注意力更集中.
17.(1);(2)
【解析】解:(1)根据圆锥体积=×底面积×高,得,
则,
故漏斗口的面积S与漏斗的深度d之间的函数关系为:;
(2)∵S=100cm2=1dm2,
∴,
解得d=3dm=30cm,
故漏斗口的面积为100cm2,那么漏斗的深为30cm.
答案第1页,共2页
答案第1页,共2页
