2021-2022学年人教版数学九年级下册28.2.2应用举例 课堂练习(word版含解析)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册28.2.2应用举例 课堂练习(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 588.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 11:16:57 | ||
图片预览




文档简介
2021-2022年初中数学九年级下册同步(人教版)
28.2.2应用举例-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知两点,若点对点的仰角为,那么对的俯角是( ).
A. B. C. D.
2.如图,当某渔船航行至B处时,测得岛C位于正北方向海里处,由于出现突发状况,该渔船请求A处的渔监船前往C处护航.已知C位于A处的东北方向上,A位于B的北偏西方向上,则A和C之间的距离为( )
A.海里 B.海里 C.海里 D.海里
3.如图,为测河两岸相对两抽水泵的距离,在距点的处,测得,则间的距离为( ).
A. B. C. D.
4.如图,已知点、点是同一幢楼上的两个不同位置,从点观测标志物的俯角是65°,从点观测标志物的俯角是35°,则的度数为( )
A.25° B.30° C.35° D.65°
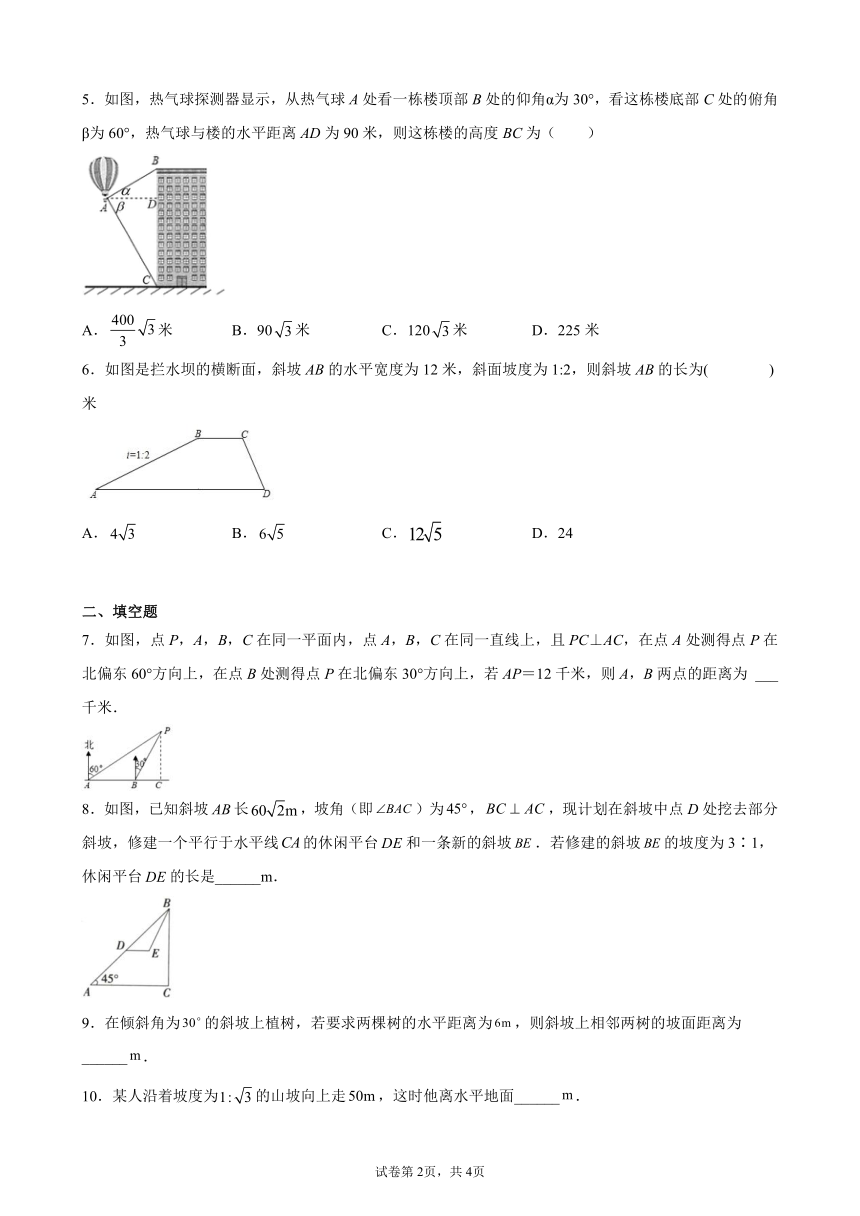
5.如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角α为30°,看这栋楼底部C处的俯角β为60°,热气球与楼的水平距离AD为90米,则这栋楼的高度BC为( )
A.米 B.90米 C.120米 D.225米
6.如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为( )米
A. B. C. D.24
二、填空题
7.如图,点P,A,B,C在同一平面内,点A,B,C在同一直线上,且PC⊥AC,在点A处测得点P在北偏东60°方向上,在点B处测得点P在北偏东30°方向上,若AP=12千米,则A,B两点的距离为 ___千米.
8.如图,已知斜坡长,坡角(即)为,,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线的休闲平台和一条新的斜坡.若修建的斜坡的坡度为3∶1,休闲平台的长是______m.
9.在倾斜角为的斜坡上植树,若要求两棵树的水平距离为,则斜坡上相邻两树的坡面距离为______.
10.某人沿着坡度为的山坡向上走,这时他离水平地面______.
11.如图,光明中学九年级(2)班的同学用自己制作的侧倾器测量该校旗杆的高度,已知测倾器CD的高度为1.54米,测点D到旗杆的水平距离BD=20米,测得旗杆顶A的仰角α=35°,则旗杆AB的高度____m(精确到0.01米).
12.如图,在市区A道路上建造一座立交桥,要求桥面的高度h为4.8米,引桥的坡角为14°,则引桥的水平距离l为____米(结果精确到0.1m,参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25).
三、解答题
13.如图,某飞机于空中A处探测到目标C,此时飞行高度,从飞机上看地平面指挥台B的俯角.求飞机A与指挥台B的距离(结果取整数).
14.如图,一块平行四边形木板的两条邻边的长分别为和,它们的夹角为,求这块木板的面积(结果保留小数点后两位)
15.如图,点A表示一个半径为的圆形森林公园的中心,在森林公园附近有B,C两个村庄,且.如果在B,C两村庄之间修一条长的笔直公路将两村连通,那么该公路是否会穿过该森林公园?
16.为方便行人横过马路,打算修建一座高的过街天桥.已知天桥的斜面坡度为,计算斜坡AB的长度(结果取整数).
17.如图,一座金字塔被发现时,顶部已经荡然无存,但底部未曾受损.已知该金字塔的下底面是一个边长为的正方形,且每一个侧面与底面成角,这座金字塔原来有多高(结果取整数)?
18.如图,拦水坝的横断面为梯形,斜面坡度是指坡面的铅直高度AF与水平宽度BF的比,斜面坡度是指DE与CE的比.根据图中数据.
求:(1)坡角和的度数;
(2)斜坡AB的长(结果保留小数点后一位).
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【解析】解:如图,
∵A对B的俯角为,
∴B对A的仰角为.
故选A.
2.A
【解析】解:如图,过点A作于点D,
由题意可知,,
在中,,
设,则.
∵,
∴,
∴,即A和C之间的距离为海里,
故选:A.
3.A
【解析】解:在中,
,
.
又,,
.
故选:.
4.B
【解析】解:如图,标注字母,由题意得:
故选:
5.C
【解析】解:如图,过点A作AD⊥BC于点D,则
在Rt△ABD中,由
在Rt△ACD中,由
∴
故这栋楼的高度为m.
故选:.
6.B
【解析】解:如图,过B作BE⊥AD于点E,
∵斜面坡度为1:2,AE=12,
∴BE=6,
在Rt△ABC中, .
故选:B.
7.
【解析】解:∵PC⊥AC,在点A处测得点P在北偏东60°方向上,
∴∠PCA=90°,∠PAC=30°,
∵AP=12千米,
∴PC=6千米,AC=6千米,
∵在点B处测得点P在北偏东30°方向上,∠PCB=90°,PC=6千米,
∴∠PBC=60°,
∴千米,
∴(千米),
故答案为:.
8.20
【解析】解:如图,延长交于点H,
在中,,,
∴,
∵点D为中点,
∴,
又∵,
∴,
∵斜坡的坡度为:,
∴,
∴,即休闲平台的长是.
故答案为:20.
9.
【解析】解:,,
,
米,
米,
故答案为:.
10.
【解析】解:如图所示:
.
.
,
.
故答案为:25.
11.15.54
【解析】解:在Rt△ACE中,∠ACE=α=35°,CE=BD=20,
∴tan∠ACE=,
∴AE=CE tan∠ACE=20 tan35°≈14.004,
∴AB=AE+BE=14.004+1.54≈15.54(米),
故答案为:15.54.
12.19.2
【解析】解:由题意可得:
tan14°=,
解得:l=19.2,
故答案为:19.2.
13.
【解析】解:在△ABC中,∵∠C=90°,∠B=∠α=16°31',AC=1200m,
∴,即sin16°31′=,
∴AB=≈4221(m);
答:飞机A与指挥台B的距离约为4221m.
14.
【解析】解:如图,设这个平行四边形各顶点分别为A、B、C、D,作于点E.
根据作图可知,AE即为平行四边形AD上的高.
在中,,
∴,
∴,
故这块木板的面积是.
15.该公路会穿过森林公园.
【解析】解:∵∠B=45°,
∴tan45°=,
∴BH=AH,
∵∠C=30°,
∴tan30°=,
∴,
∴BC=BH+HC=,
∵BC=500,
∴,
∴,
∵<300,
∴该公路会穿过该森林公园.
16.
【解析】解:如图所示:
∵i=1:1.5,BC=5m,
∴BC:AC=5:AC=1:1.5,
解得:AC=7.5(m),
则AB=(m),
答:斜坡AB的长度约为9m.
17.
【解析】解:如图所示
∵底部是边长为130m的正方形,
∴BC=m,
∵AC⊥BC,∠ABC=65°,
∴AC=BC tan65°≈139m.
答:这个金字塔原来有139米高.
18.(1),;(2)
【解析】(1)∵斜面AB坡度,
斜面CD坡度,
∴,,
∴,;
(2)∵,
∴,
∴;
答案第1页,共2页
答案第1页,共2页
28.2.2应用举例-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知两点,若点对点的仰角为,那么对的俯角是( ).
A. B. C. D.
2.如图,当某渔船航行至B处时,测得岛C位于正北方向海里处,由于出现突发状况,该渔船请求A处的渔监船前往C处护航.已知C位于A处的东北方向上,A位于B的北偏西方向上,则A和C之间的距离为( )
A.海里 B.海里 C.海里 D.海里
3.如图,为测河两岸相对两抽水泵的距离,在距点的处,测得,则间的距离为( ).
A. B. C. D.
4.如图,已知点、点是同一幢楼上的两个不同位置,从点观测标志物的俯角是65°,从点观测标志物的俯角是35°,则的度数为( )
A.25° B.30° C.35° D.65°
5.如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角α为30°,看这栋楼底部C处的俯角β为60°,热气球与楼的水平距离AD为90米,则这栋楼的高度BC为( )
A.米 B.90米 C.120米 D.225米
6.如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为( )米
A. B. C. D.24
二、填空题
7.如图,点P,A,B,C在同一平面内,点A,B,C在同一直线上,且PC⊥AC,在点A处测得点P在北偏东60°方向上,在点B处测得点P在北偏东30°方向上,若AP=12千米,则A,B两点的距离为 ___千米.
8.如图,已知斜坡长,坡角(即)为,,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线的休闲平台和一条新的斜坡.若修建的斜坡的坡度为3∶1,休闲平台的长是______m.
9.在倾斜角为的斜坡上植树,若要求两棵树的水平距离为,则斜坡上相邻两树的坡面距离为______.
10.某人沿着坡度为的山坡向上走,这时他离水平地面______.
11.如图,光明中学九年级(2)班的同学用自己制作的侧倾器测量该校旗杆的高度,已知测倾器CD的高度为1.54米,测点D到旗杆的水平距离BD=20米,测得旗杆顶A的仰角α=35°,则旗杆AB的高度____m(精确到0.01米).
12.如图,在市区A道路上建造一座立交桥,要求桥面的高度h为4.8米,引桥的坡角为14°,则引桥的水平距离l为____米(结果精确到0.1m,参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25).
三、解答题
13.如图,某飞机于空中A处探测到目标C,此时飞行高度,从飞机上看地平面指挥台B的俯角.求飞机A与指挥台B的距离(结果取整数).
14.如图,一块平行四边形木板的两条邻边的长分别为和,它们的夹角为,求这块木板的面积(结果保留小数点后两位)
15.如图,点A表示一个半径为的圆形森林公园的中心,在森林公园附近有B,C两个村庄,且.如果在B,C两村庄之间修一条长的笔直公路将两村连通,那么该公路是否会穿过该森林公园?
16.为方便行人横过马路,打算修建一座高的过街天桥.已知天桥的斜面坡度为,计算斜坡AB的长度(结果取整数).
17.如图,一座金字塔被发现时,顶部已经荡然无存,但底部未曾受损.已知该金字塔的下底面是一个边长为的正方形,且每一个侧面与底面成角,这座金字塔原来有多高(结果取整数)?
18.如图,拦水坝的横断面为梯形,斜面坡度是指坡面的铅直高度AF与水平宽度BF的比,斜面坡度是指DE与CE的比.根据图中数据.
求:(1)坡角和的度数;
(2)斜坡AB的长(结果保留小数点后一位).
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【解析】解:如图,
∵A对B的俯角为,
∴B对A的仰角为.
故选A.
2.A
【解析】解:如图,过点A作于点D,
由题意可知,,
在中,,
设,则.
∵,
∴,
∴,即A和C之间的距离为海里,
故选:A.
3.A
【解析】解:在中,
,
.
又,,
.
故选:.
4.B
【解析】解:如图,标注字母,由题意得:
故选:
5.C
【解析】解:如图,过点A作AD⊥BC于点D,则
在Rt△ABD中,由
在Rt△ACD中,由
∴
故这栋楼的高度为m.
故选:.
6.B
【解析】解:如图,过B作BE⊥AD于点E,
∵斜面坡度为1:2,AE=12,
∴BE=6,
在Rt△ABC中, .
故选:B.
7.
【解析】解:∵PC⊥AC,在点A处测得点P在北偏东60°方向上,
∴∠PCA=90°,∠PAC=30°,
∵AP=12千米,
∴PC=6千米,AC=6千米,
∵在点B处测得点P在北偏东30°方向上,∠PCB=90°,PC=6千米,
∴∠PBC=60°,
∴千米,
∴(千米),
故答案为:.
8.20
【解析】解:如图,延长交于点H,
在中,,,
∴,
∵点D为中点,
∴,
又∵,
∴,
∵斜坡的坡度为:,
∴,
∴,即休闲平台的长是.
故答案为:20.
9.
【解析】解:,,
,
米,
米,
故答案为:.
10.
【解析】解:如图所示:
.
.
,
.
故答案为:25.
11.15.54
【解析】解:在Rt△ACE中,∠ACE=α=35°,CE=BD=20,
∴tan∠ACE=,
∴AE=CE tan∠ACE=20 tan35°≈14.004,
∴AB=AE+BE=14.004+1.54≈15.54(米),
故答案为:15.54.
12.19.2
【解析】解:由题意可得:
tan14°=,
解得:l=19.2,
故答案为:19.2.
13.
【解析】解:在△ABC中,∵∠C=90°,∠B=∠α=16°31',AC=1200m,
∴,即sin16°31′=,
∴AB=≈4221(m);
答:飞机A与指挥台B的距离约为4221m.
14.
【解析】解:如图,设这个平行四边形各顶点分别为A、B、C、D,作于点E.
根据作图可知,AE即为平行四边形AD上的高.
在中,,
∴,
∴,
故这块木板的面积是.
15.该公路会穿过森林公园.
【解析】解:∵∠B=45°,
∴tan45°=,
∴BH=AH,
∵∠C=30°,
∴tan30°=,
∴,
∴BC=BH+HC=,
∵BC=500,
∴,
∴,
∵<300,
∴该公路会穿过该森林公园.
16.
【解析】解:如图所示:
∵i=1:1.5,BC=5m,
∴BC:AC=5:AC=1:1.5,
解得:AC=7.5(m),
则AB=(m),
答:斜坡AB的长度约为9m.
17.
【解析】解:如图所示
∵底部是边长为130m的正方形,
∴BC=m,
∵AC⊥BC,∠ABC=65°,
∴AC=BC tan65°≈139m.
答:这个金字塔原来有139米高.
18.(1),;(2)
【解析】(1)∵斜面AB坡度,
斜面CD坡度,
∴,,
∴,;
(2)∵,
∴,
∴;
答案第1页,共2页
答案第1页,共2页
