人教版八年级上册数学11.1.1三角形的边教学设计
文档属性
| 名称 | 人教版八年级上册数学11.1.1三角形的边教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 67.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 14:05:33 | ||
图片预览

文档简介
11.1.1三角形的边
一 教材分析
1 教材的地位和作用
本节课是在小学初步认识三角形的基础上,又具体介绍了三角形的有关概念和三角形三边的关系。它既是上学期所学线段和角的延续,又是后继学习全等三角形和四边形的基础。在知识体系上具有承上启下的作用。
2 教学目标
知识目标:理解三角形的有关概念,掌握三角形三边的关系。
能力目标:通过观察、操作、讨论等活动,培养学生的动手实践能力和语言表达能力。
情感目标:让学生在自主参与、合作交流的活动中,体验成功的喜悦,树立自信,激发学习数学的兴趣。
3 教学重、难点
教学重点:三角形三边关系的探究和归纳.
教学难点:三角形三边关系的应用.
二、教学方法
以引导发现为主,讨论演示相结合.
三、教学过程
(1) 创设情境 引入新课
1. 有人不遵守交通规则,冒着生命危险斜穿马路.你能用所学的数学知识解释这种不文明的行为吗
2.展示学习目标:
1、认识三角形的边、内角、顶点,能用符号语言表示三角形。
2、掌握三角形三边的关系定理,能利用定理及其推论进行简单的证明。
3、了解三角形按边分类的原则和结论。
(二) 探究新知
1.三角形有关的概念
(1)定义: 不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
(2) 表示方法: △ABC 读法:读作三角形ABC
(3) 元素: 三条边、三个顶点、三个内角.
2.合作探究三角形三边的关系
《数学课程标准》指出:“有意义的学习活动不能单纯地依赖模仿和记忆”。动手实践、自主探究、合作交流是学习数学的重要方式。为了充分体现新课标的要求,培养学生的动手实践能力、逻辑思维能力,在探究三角形三边关系时,我设置了以下活动:
活动一:
(画一画,量一量, 算一算)
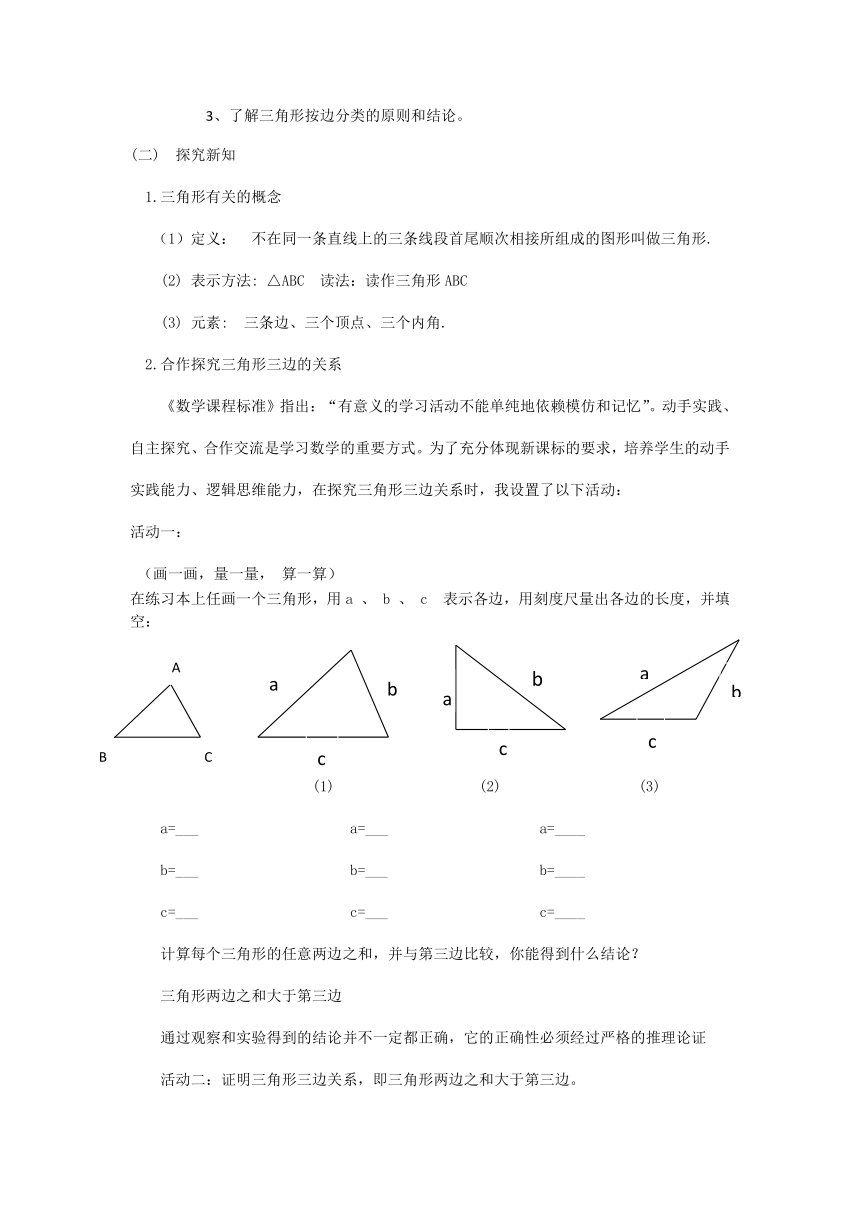
在练习本上任画一个三角形,用a 、 b 、 c 表示各边,用刻度尺量出各边的长度,并填空:
(1) (2) (3)
a=___ a=___ a=____
b=___ b=___ b=____
c=___ c=___ c=____
计算每个三角形的任意两边之和,并与第三边比较,你能得到什么结论?
三角形两边之和大于第三边
通过观察和实验得到的结论并不一定都正确,它的正确性必须经过严格的推理论证
活动二:证明三角形三边关系,即三角形两边之和大于第三边。
活动三:根据不等式基本性质,很容易得到三角形三边关系:三角形两边之差小于第三边。但是两边的差谁减谁才有意义,结合图形已知应增加什么条件,求证写成什么?
通过上述活动得三角形三边关系:
三角形两边之和大于第三边,三角形两边之差小于第三边。
活动四:归纳总结:
三角形中已知两边,确定第三边的条件
两边之差<第三边<两边之和
3.探究:三角形的分类
(三)拓展创新 应用新知
例1.
1.图中有几个三角形?用符号表示这些三角形。
2.以AB为边的三角形有哪些?
3.以E为顶点的三角形有哪些?
4.说出△ BCD的三个角。
例2.
5.下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
技巧: 比较较短两条线段之和与最长线段的大小,
或比较较长两条线段之差与最短线段的大小.
例3.
6、三角形的三边长分别为3cm、8cm、xcm,
那么x应满足的不等式是____ ,x可能取的整数值共有____个。
例4.
7、等腰三角形某两边之长分别为6cm和8cm,那么周长等于____。
8、等腰三角形某两边之长分别为4cm和8cm,那么周长等于____。
[设计意图]
设计不同层次的练习时,巧设坡度,降低难度,弱化学习障碍的影响,以帮助学生从易到难、从会学到会用、从知识到能力的迁移。从而实现人人学有价值的数学,人人都能获得必需的数学,不同的人在数学上得到不同的发展。
例5
9、已知:如图,D是△ABC中AB边上的一点,且DB=DC。
求证:DB﹥AC-AD
[设计意图]让学生多角度、全方位发挥其思维的深度和广度。拓宽学生的认知领域,发挥教材的扩张作用,培养学生的发散思维能力。
(四)板书设计
(一) (二)
三角形有关的概念
1定义
2表示方法
3元素
(三)
说明
本节教学目标有两个:1、认识三角形及其相关概念。 2、掌握三角形三边的关系。其中,完成两个任务:2.1掌握三角形三边关系定理,能利用定理及其推论进行简单的证明,2.2会按边对三角形进行分类。重点是三角形三边之间的关系。难点:运用三角形三边之间的不等关系解题。
三边关系是很简单的,就几何事实也是很直观的,三角形的定义和三边关系如果简单处理,通过加强机械性训练的方式教学,固然能腾出时间,但总的说来,降低了学生思维训练上的要求。像这样的教学内容,应该怎样处理,才能有利于培养能力,训练思维呢?
首先,应该突出整体性,即深刻揭示概念(三角形的定义)和理论(三边关系定理和推论)之间的逻辑联系,揭示理论和方法之间的内在关系,把概念、理论、方法组织成一个结构明确、逻辑和谐的整体。一种概念之所以得到发展,其原因在于概念的内涵中蕴含着矛盾,三角形定义中的矛盾表现在不是任何三条线段都能首尾顺次连接而组成三角形的,这就预示三角形三边之间应存在着某种关系,一旦和线段最短公理综合,这个关系就会明显地展现出来。另外,有了定理和推论,要想把理论转化为解题方法,还要注意到定理的等价命题及定理和推论的综合应用。
其次,在数学中应揭示解决问题的思维过程,思维过程和思维结果的辩证统一是“教”和“学”的双方都应该遵循的基本原则。数学教学的过程应该思维过程不断展开的过程,思维过程展开了。就会创造出许多有利于培养能力、训练思维的学习情境。本课中,我们把思维的起点定在三角形的概念上,随着矛盾的揭示,思维的深入,力争达到内化,而这个内化是在整体性、逻辑必然性的基础上完成的。
再次,应挖掘教材中有利于能力培养,思维训练的各种因素,以指导教学方法的设计。本课中,定理和推论的获得没有完整的证明格式,且推论在教材中说理不够严谨,两边的差在实际问题中应满足长边减短边才有意义;以及如何对三角形进行合理的分类等,都是培养能力和训练思维的用武之地。为此,在本课的教学过程中,考虑到要让学生在动手、动脑的基础上。去锻炼他们的归纳、概括能力,同时提高语言表述能力,并注重加强思维的严密性的训练和几何证明的规范化的训练。
a
b
c
a
b
c
a
b
c
A
B
C
不等边三角形
等腰三角形{
腰和底不相等的等腰三角形
等边三角形
按边分{
B
A
D
E
C
B
A
C
D
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边
确定第三边的条件:
两边之差<第三边<两边之和
三角形三边的关系
A
C
B
不等边三角形
等腰三角形{
腰和底不相等的等腰三角形
等边三角形
按边分{
一 教材分析
1 教材的地位和作用
本节课是在小学初步认识三角形的基础上,又具体介绍了三角形的有关概念和三角形三边的关系。它既是上学期所学线段和角的延续,又是后继学习全等三角形和四边形的基础。在知识体系上具有承上启下的作用。
2 教学目标
知识目标:理解三角形的有关概念,掌握三角形三边的关系。
能力目标:通过观察、操作、讨论等活动,培养学生的动手实践能力和语言表达能力。
情感目标:让学生在自主参与、合作交流的活动中,体验成功的喜悦,树立自信,激发学习数学的兴趣。
3 教学重、难点
教学重点:三角形三边关系的探究和归纳.
教学难点:三角形三边关系的应用.
二、教学方法
以引导发现为主,讨论演示相结合.
三、教学过程
(1) 创设情境 引入新课
1. 有人不遵守交通规则,冒着生命危险斜穿马路.你能用所学的数学知识解释这种不文明的行为吗
2.展示学习目标:
1、认识三角形的边、内角、顶点,能用符号语言表示三角形。
2、掌握三角形三边的关系定理,能利用定理及其推论进行简单的证明。
3、了解三角形按边分类的原则和结论。
(二) 探究新知
1.三角形有关的概念
(1)定义: 不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
(2) 表示方法: △ABC 读法:读作三角形ABC
(3) 元素: 三条边、三个顶点、三个内角.
2.合作探究三角形三边的关系
《数学课程标准》指出:“有意义的学习活动不能单纯地依赖模仿和记忆”。动手实践、自主探究、合作交流是学习数学的重要方式。为了充分体现新课标的要求,培养学生的动手实践能力、逻辑思维能力,在探究三角形三边关系时,我设置了以下活动:
活动一:
(画一画,量一量, 算一算)
在练习本上任画一个三角形,用a 、 b 、 c 表示各边,用刻度尺量出各边的长度,并填空:
(1) (2) (3)
a=___ a=___ a=____
b=___ b=___ b=____
c=___ c=___ c=____
计算每个三角形的任意两边之和,并与第三边比较,你能得到什么结论?
三角形两边之和大于第三边
通过观察和实验得到的结论并不一定都正确,它的正确性必须经过严格的推理论证
活动二:证明三角形三边关系,即三角形两边之和大于第三边。
活动三:根据不等式基本性质,很容易得到三角形三边关系:三角形两边之差小于第三边。但是两边的差谁减谁才有意义,结合图形已知应增加什么条件,求证写成什么?
通过上述活动得三角形三边关系:
三角形两边之和大于第三边,三角形两边之差小于第三边。
活动四:归纳总结:
三角形中已知两边,确定第三边的条件
两边之差<第三边<两边之和
3.探究:三角形的分类
(三)拓展创新 应用新知
例1.
1.图中有几个三角形?用符号表示这些三角形。
2.以AB为边的三角形有哪些?
3.以E为顶点的三角形有哪些?
4.说出△ BCD的三个角。
例2.
5.下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
技巧: 比较较短两条线段之和与最长线段的大小,
或比较较长两条线段之差与最短线段的大小.
例3.
6、三角形的三边长分别为3cm、8cm、xcm,
那么x应满足的不等式是____ ,x可能取的整数值共有____个。
例4.
7、等腰三角形某两边之长分别为6cm和8cm,那么周长等于____。
8、等腰三角形某两边之长分别为4cm和8cm,那么周长等于____。
[设计意图]
设计不同层次的练习时,巧设坡度,降低难度,弱化学习障碍的影响,以帮助学生从易到难、从会学到会用、从知识到能力的迁移。从而实现人人学有价值的数学,人人都能获得必需的数学,不同的人在数学上得到不同的发展。
例5
9、已知:如图,D是△ABC中AB边上的一点,且DB=DC。
求证:DB﹥AC-AD
[设计意图]让学生多角度、全方位发挥其思维的深度和广度。拓宽学生的认知领域,发挥教材的扩张作用,培养学生的发散思维能力。
(四)板书设计
(一) (二)
三角形有关的概念
1定义
2表示方法
3元素
(三)
说明
本节教学目标有两个:1、认识三角形及其相关概念。 2、掌握三角形三边的关系。其中,完成两个任务:2.1掌握三角形三边关系定理,能利用定理及其推论进行简单的证明,2.2会按边对三角形进行分类。重点是三角形三边之间的关系。难点:运用三角形三边之间的不等关系解题。
三边关系是很简单的,就几何事实也是很直观的,三角形的定义和三边关系如果简单处理,通过加强机械性训练的方式教学,固然能腾出时间,但总的说来,降低了学生思维训练上的要求。像这样的教学内容,应该怎样处理,才能有利于培养能力,训练思维呢?
首先,应该突出整体性,即深刻揭示概念(三角形的定义)和理论(三边关系定理和推论)之间的逻辑联系,揭示理论和方法之间的内在关系,把概念、理论、方法组织成一个结构明确、逻辑和谐的整体。一种概念之所以得到发展,其原因在于概念的内涵中蕴含着矛盾,三角形定义中的矛盾表现在不是任何三条线段都能首尾顺次连接而组成三角形的,这就预示三角形三边之间应存在着某种关系,一旦和线段最短公理综合,这个关系就会明显地展现出来。另外,有了定理和推论,要想把理论转化为解题方法,还要注意到定理的等价命题及定理和推论的综合应用。
其次,在数学中应揭示解决问题的思维过程,思维过程和思维结果的辩证统一是“教”和“学”的双方都应该遵循的基本原则。数学教学的过程应该思维过程不断展开的过程,思维过程展开了。就会创造出许多有利于培养能力、训练思维的学习情境。本课中,我们把思维的起点定在三角形的概念上,随着矛盾的揭示,思维的深入,力争达到内化,而这个内化是在整体性、逻辑必然性的基础上完成的。
再次,应挖掘教材中有利于能力培养,思维训练的各种因素,以指导教学方法的设计。本课中,定理和推论的获得没有完整的证明格式,且推论在教材中说理不够严谨,两边的差在实际问题中应满足长边减短边才有意义;以及如何对三角形进行合理的分类等,都是培养能力和训练思维的用武之地。为此,在本课的教学过程中,考虑到要让学生在动手、动脑的基础上。去锻炼他们的归纳、概括能力,同时提高语言表述能力,并注重加强思维的严密性的训练和几何证明的规范化的训练。
a
b
c
a
b
c
a
b
c
A
B
C
不等边三角形
等腰三角形{
腰和底不相等的等腰三角形
等边三角形
按边分{
B
A
D
E
C
B
A
C
D
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边
确定第三边的条件:
两边之差<第三边<两边之和
三角形三边的关系
A
C
B
不等边三角形
等腰三角形{
腰和底不相等的等腰三角形
等边三角形
按边分{
