华东师大版 八年级数学 第18-19章平行四边形、矩形、菱形、正方形复习 教学设计(表格式)
文档属性
| 名称 | 华东师大版 八年级数学 第18-19章平行四边形、矩形、菱形、正方形复习 教学设计(表格式) | 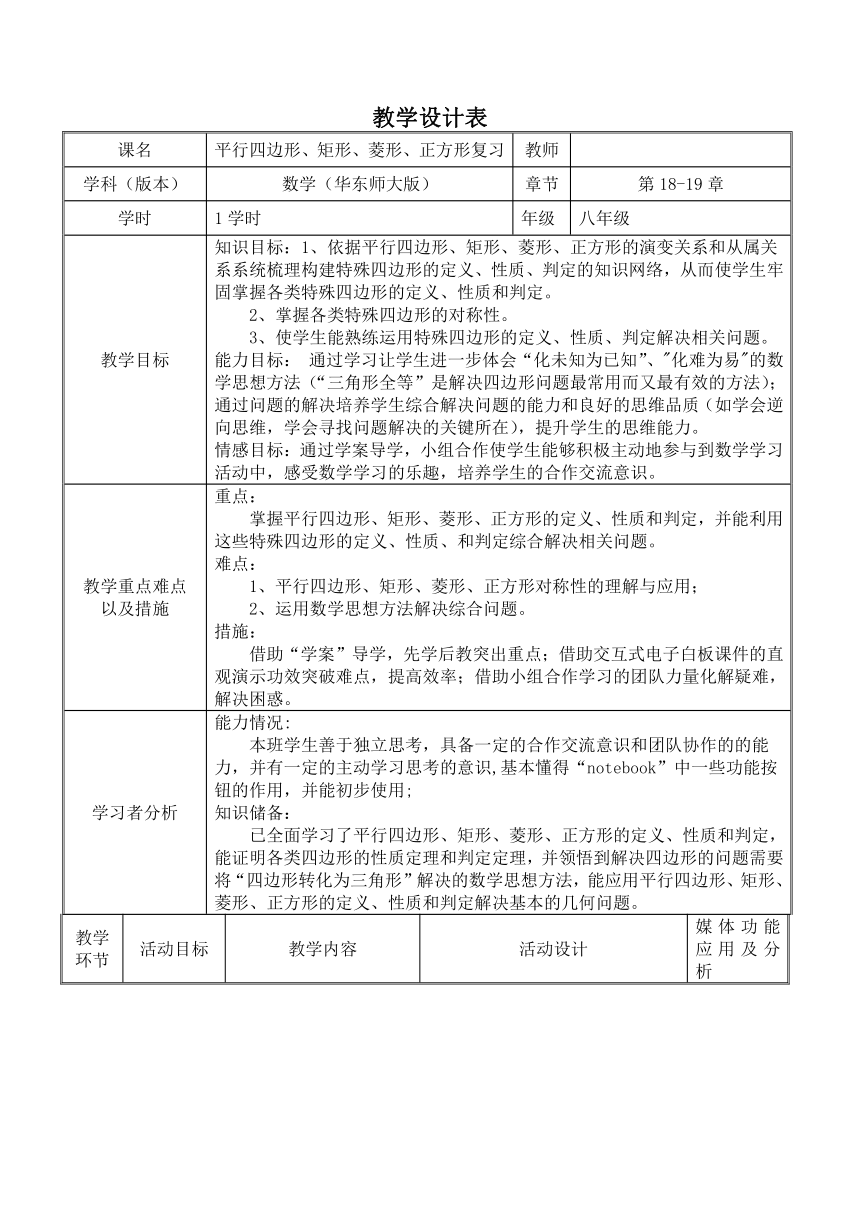 | |
| 格式 | doc | ||
| 文件大小 | 69.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 14:17:17 | ||
图片预览


文档简介
教学设计表
课名 平行四边形、矩形、菱形、正方形复习 教师
学科(版本) 数学(华东师大版) 章节 第18-19章
学时 1学时 年级 八年级
教学目标 知识目标:1、依据平行四边形、矩形、菱形、正方形的演变关系和从属关系系统梳理构建特殊四边形的定义、性质、判定的知识网络,从而使学生牢固掌握各类特殊四边形的定义、性质和判定。 2、掌握各类特殊四边形的对称性。 3、使学生能熟练运用特殊四边形的定义、性质、判定解决相关问题。能力目标: 通过学习让学生进一步体会“化未知为已知”、"化难为易"的数学思想方法(“三角形全等”是解决四边形问题最常用而又最有效的方法);通过问题的解决培养学生综合解决问题的能力和良好的思维品质(如学会逆向思维,学会寻找问题解决的关键所在),提升学生的思维能力。情感目标:通过学案导学,小组合作使学生能够积极主动地参与到数学学习活动中,感受数学学习的乐趣,培养学生的合作交流意识。
教学重点难点以及措施 重点: 掌握平行四边形、矩形、菱形、正方形的定义、性质和判定,并能利用这些特殊四边形的定义、性质、和判定综合解决相关问题。难点: 1、平行四边形、矩形、菱形、正方形对称性的理解与应用;2、运用数学思想方法解决综合问题。措施: 借助“学案”导学,先学后教突出重点;借助交互式电子白板课件的直观演示功效突破难点,提高效率;借助小组合作学习的团队力量化解疑难,解决困惑。
学习者分析 能力情况: 本班学生善于独立思考,具备一定的合作交流意识和团队协作的的能力,并有一定的主动学习思考的意识,基本懂得“notebook”中一些功能按钮的作用,并能初步使用;知识储备: 已全面学行四边形、矩形、菱形、正方形的定义、性质和判定,能证明各类四边形的性质定理和判定定理,并领悟到解决四边形的问题需要将“四边形转化为三角形”解决的数学思想方法,能应用平行四边形、矩形、菱形、正方形的定义、性质和判定解决基本的几何问题。
教学环节 活动目标 教学内容 活动设计 媒体功能应用及分析
(一)知识梳理--1 利用关系网进一步理清各类四边形之间的联系,牢固掌握各类四边形的定义、性质和判定以及之间的联系,学会聆听他人的发言并能进行恰当的补充。 利用各类四边形的演变关系,梳理特殊四边形定义、性质、判定关系网络 课前:教师活动:设计学案学生活动:按照“学案”导学全面梳理各类四边形的定义、性质、判定并填入关系网中。课中:教师活动:引导学生完善关系网。学生活动:对各类四边形之间的关系、性质、判定、特殊之处做陈述。 利用交互式电子白板的绘图功能形成四边形的关系网,利用“笔”的书写功能作注释。
(一)知识梳理--2 弄清各类特殊四边形之间的从属关系,有利于学生进一步理解掌握各类特殊四边形之间的联系,巩固其定义、性质和判定。 若每个圆圈代表一类四边形的集合,将四边形、平行四边形、矩形、菱形、正方形填入下列圆圈中。 课前:教师活动:设计学案学生活动:按照“学案”导学在圆圈中填入四边形的名称。课中:教师活动:针对学生完成的内容作分析指导。学生活动:请某小组一学生在白板上展示,并对填入的内容进行阐述,其余学生做完善补充。 在填入四边形名称时直接利用交互式电子白板的 “笔”的书写功能非常方便。
(一)知识梳理--3 进一步掌握平行四边形、矩形、菱形的对称性,以“平分面积”这个问题为引子来突破本章节的一个难点。 梳理总结平行四边形、矩形、菱形的对称性。内容如下:平行四边形、矩形、菱形、正方形都是 对称图形(正方形绕中心旋转 度能与自身完全重合),其中 是轴对称(正方形的对称轴有 条)。请用一条直线将下列四边形的面积平均分成相等的两部分,并说明这条直线的特征和面积相等的理由。(其中正方形用两条直线将其面积平均分成相等的四部分)。 课前:教师活动:设计学案学生活动:按照“学案”导学全面梳理各类四边形的对称性,并独立解决所提出的问题。课中:教师活动:针对学生回答的内容作斧正指导,并适时提出新的问题思考,动态演示平行四边形的中心对称性、正方形的旋转对称性以及分得的面积相等的理由。学生活动:分小组讨论直线的特征和面积相等的理由。并由小组代表发言,其余同学认真聆听并作补充。(预设:若学生认为只需做出对角线就能将面积分成相等的两部分,教师应进一步提出问题“难道必须是对角线吗?”促使学生进一步深层次思考发现问题的本质是“平行四边形是中心对称图形,只要过中心的任意直线都可平分面积”,在叙述理由时除了用平行四边形具有中心对称性来说理外,还应该用演绎推理说理,即利用三角形全等进行证明。) 利用白板的“文字动画效果”填横线上的空白,点击即可完成。利用“线”和“笔”工具随意分割面积并作标识和注释。利用链接功能链接到“.gsp”文件,丰富白板的内容,“.gsp”文件在白板环境下使用更方便,更自如。
(二)应用练习--1 进一步掌握菱形的性质与判定以及矩形与菱形各自的特殊之处,熟知矩形、菱形的性质和判定是解决问题的关键。 1、已知一块矩形形状的废料,现从这块废料上裁出一块面积足够大的菱形材料,请用尺规做出改造后的菱形。(要求保留作图痕迹) 课前:教师活动:设计学案学生活动:按照“学案”导学独立解决应用练习1所提出的问题。课中:教师活动:帮助学生理解生活中“足够大”的意义,针对学生回答的内容作斧正指导,并适时提出新的问题思考。学生活动:小组代表阐述改造的方法和理由,其余学生认真聆听并作补充。(预设:大部分学生很容易想到连接矩形四条边的中点便可得到一个菱形,此时应及时引导学生菱形除了边具有特殊性外,对角线也具有特殊性,也应考虑可否从矩形对角线上去改造,另外这里只要求学生裁出面积足够大的菱形,也不妨让学生进一步思考有没有面积最大的菱形,从而拓开学生的思维。) 利用白板的“直尺、圆规”、“线”工具进行作图,“笔”工具做标识和注释。
(二)应用练习--2 让学生能够综合运用平行四边形、矩形、菱形、正方形的判定解决问题,领悟到“三角形全等”是解决四边形问题常用而有效地方法,在综合解决问题时若给了结论而需补充条件应学会“逆向思维”。 2、已知△ABC,以三边为边分别作等边△ACD、△ABF、△BCE,判断四边形ADEF的形状。探究:①是否一定存在平行四边形ADEF,若存在写出△ABC应满足的条件;若不一定存在,请说明理由。②△ABC满足什么条件时,四边形ADEF是矩形?③△ABC满足什么条件时,四边形ADEF是菱形?④△ABC满足什么条件时,四边形ADEF是正方形? 课前:教师活动:设计学案,指导学生完成学案。学生活动:按照“学案”导学独立解决应用练习2所提出的问题。课中:教师活动1:针对学生回答的内容作斧正指导。学生活动1:小组代表讲解“判断四边形ADEF的形状”的方法和理由,其余学生认真聆听并作补充。教师活动2:动态演示满足矩形、菱形、正方形的条件,并适时提出新问题。学生活动2:小组代表讲解“△ABC满足什么条件时,四边形ADEF是矩形、菱形、正方形?”并阐述理由和思考的方法,其余学生认真聆听并作补充。 利用白板的“笔”工具边讲解边注释;利用链接功能链接到“.gsp”文件,丰富白板的内容,“.gsp”文件在白板环境下进行动态演示和书写更方便,效果更好。
(三)作业思考 以“特殊四边形为载体”进行全等探究是一类常见的问题,这里需要学生牢固掌握各特殊四边形的性质特征,另外以“改变问题条件继续对原问题结论进行探究”的探究问题也很常见,这里应让学生领悟到在解决探究问题时应使用类比思想,按照原问题的思路方法进行,找准原问题得以解决的关键和实质。 已知:如图①,正方形ABCD,点G、E分别是边AB、BC的中点,过E点作AE的垂线交正方形外角的平分线于点F.求证:AE=EF 探究:①若E是BC上任意一点(不与B、C重合),过E点作AE的垂线交正方形外角的平分线于点F,AE与EF相等吗?(在图②中完成)②若E是BC延长线上一点,过E点作AE的垂线交正方形外角的平分线于点F,AE与EF相等吗?(在图③中完成) 课前:教师活动:设计学案,指导学生完成学案。学生活动:按照“学案”导学独立解决作业思考所提出的问题。课中:教师活动:针对学生回答的内容作斧正指导,引导学生找出问题得以解决的关键实质所在。学生活动:1、分小组合作交流独立解决问题过程中的收获和思考问题的方法,学生彼此之间碰撞出思维的火花。2、小组代表讲解问题得以证明缘由和思考的方法,分析探究①和探究②与原始问题有何联系,又有何不同,从而师生共同寻找两个探究问题解决的思路方法(即两个三角形全等最主要的原因是AG=CE或BG=BE,进而确定出点G的位置)。 利用白板的“笔” “线”“圆规、直尺”工具画图,作注释。
(四)小结反思 养成课课总结与反思的好习惯,促进学生不断进步与提高。 谈谈本节课的收获 还存在的问题有哪些? 教师活动:认真倾听学生的发言,并进行答疑解惑。学生活动:以个体为单位自由发言,谈自己的收获与提高以及还存在的问题。
课名 平行四边形、矩形、菱形、正方形复习 教师
学科(版本) 数学(华东师大版) 章节 第18-19章
学时 1学时 年级 八年级
教学目标 知识目标:1、依据平行四边形、矩形、菱形、正方形的演变关系和从属关系系统梳理构建特殊四边形的定义、性质、判定的知识网络,从而使学生牢固掌握各类特殊四边形的定义、性质和判定。 2、掌握各类特殊四边形的对称性。 3、使学生能熟练运用特殊四边形的定义、性质、判定解决相关问题。能力目标: 通过学习让学生进一步体会“化未知为已知”、"化难为易"的数学思想方法(“三角形全等”是解决四边形问题最常用而又最有效的方法);通过问题的解决培养学生综合解决问题的能力和良好的思维品质(如学会逆向思维,学会寻找问题解决的关键所在),提升学生的思维能力。情感目标:通过学案导学,小组合作使学生能够积极主动地参与到数学学习活动中,感受数学学习的乐趣,培养学生的合作交流意识。
教学重点难点以及措施 重点: 掌握平行四边形、矩形、菱形、正方形的定义、性质和判定,并能利用这些特殊四边形的定义、性质、和判定综合解决相关问题。难点: 1、平行四边形、矩形、菱形、正方形对称性的理解与应用;2、运用数学思想方法解决综合问题。措施: 借助“学案”导学,先学后教突出重点;借助交互式电子白板课件的直观演示功效突破难点,提高效率;借助小组合作学习的团队力量化解疑难,解决困惑。
学习者分析 能力情况: 本班学生善于独立思考,具备一定的合作交流意识和团队协作的的能力,并有一定的主动学习思考的意识,基本懂得“notebook”中一些功能按钮的作用,并能初步使用;知识储备: 已全面学行四边形、矩形、菱形、正方形的定义、性质和判定,能证明各类四边形的性质定理和判定定理,并领悟到解决四边形的问题需要将“四边形转化为三角形”解决的数学思想方法,能应用平行四边形、矩形、菱形、正方形的定义、性质和判定解决基本的几何问题。
教学环节 活动目标 教学内容 活动设计 媒体功能应用及分析
(一)知识梳理--1 利用关系网进一步理清各类四边形之间的联系,牢固掌握各类四边形的定义、性质和判定以及之间的联系,学会聆听他人的发言并能进行恰当的补充。 利用各类四边形的演变关系,梳理特殊四边形定义、性质、判定关系网络 课前:教师活动:设计学案学生活动:按照“学案”导学全面梳理各类四边形的定义、性质、判定并填入关系网中。课中:教师活动:引导学生完善关系网。学生活动:对各类四边形之间的关系、性质、判定、特殊之处做陈述。 利用交互式电子白板的绘图功能形成四边形的关系网,利用“笔”的书写功能作注释。
(一)知识梳理--2 弄清各类特殊四边形之间的从属关系,有利于学生进一步理解掌握各类特殊四边形之间的联系,巩固其定义、性质和判定。 若每个圆圈代表一类四边形的集合,将四边形、平行四边形、矩形、菱形、正方形填入下列圆圈中。 课前:教师活动:设计学案学生活动:按照“学案”导学在圆圈中填入四边形的名称。课中:教师活动:针对学生完成的内容作分析指导。学生活动:请某小组一学生在白板上展示,并对填入的内容进行阐述,其余学生做完善补充。 在填入四边形名称时直接利用交互式电子白板的 “笔”的书写功能非常方便。
(一)知识梳理--3 进一步掌握平行四边形、矩形、菱形的对称性,以“平分面积”这个问题为引子来突破本章节的一个难点。 梳理总结平行四边形、矩形、菱形的对称性。内容如下:平行四边形、矩形、菱形、正方形都是 对称图形(正方形绕中心旋转 度能与自身完全重合),其中 是轴对称(正方形的对称轴有 条)。请用一条直线将下列四边形的面积平均分成相等的两部分,并说明这条直线的特征和面积相等的理由。(其中正方形用两条直线将其面积平均分成相等的四部分)。 课前:教师活动:设计学案学生活动:按照“学案”导学全面梳理各类四边形的对称性,并独立解决所提出的问题。课中:教师活动:针对学生回答的内容作斧正指导,并适时提出新的问题思考,动态演示平行四边形的中心对称性、正方形的旋转对称性以及分得的面积相等的理由。学生活动:分小组讨论直线的特征和面积相等的理由。并由小组代表发言,其余同学认真聆听并作补充。(预设:若学生认为只需做出对角线就能将面积分成相等的两部分,教师应进一步提出问题“难道必须是对角线吗?”促使学生进一步深层次思考发现问题的本质是“平行四边形是中心对称图形,只要过中心的任意直线都可平分面积”,在叙述理由时除了用平行四边形具有中心对称性来说理外,还应该用演绎推理说理,即利用三角形全等进行证明。) 利用白板的“文字动画效果”填横线上的空白,点击即可完成。利用“线”和“笔”工具随意分割面积并作标识和注释。利用链接功能链接到“.gsp”文件,丰富白板的内容,“.gsp”文件在白板环境下使用更方便,更自如。
(二)应用练习--1 进一步掌握菱形的性质与判定以及矩形与菱形各自的特殊之处,熟知矩形、菱形的性质和判定是解决问题的关键。 1、已知一块矩形形状的废料,现从这块废料上裁出一块面积足够大的菱形材料,请用尺规做出改造后的菱形。(要求保留作图痕迹) 课前:教师活动:设计学案学生活动:按照“学案”导学独立解决应用练习1所提出的问题。课中:教师活动:帮助学生理解生活中“足够大”的意义,针对学生回答的内容作斧正指导,并适时提出新的问题思考。学生活动:小组代表阐述改造的方法和理由,其余学生认真聆听并作补充。(预设:大部分学生很容易想到连接矩形四条边的中点便可得到一个菱形,此时应及时引导学生菱形除了边具有特殊性外,对角线也具有特殊性,也应考虑可否从矩形对角线上去改造,另外这里只要求学生裁出面积足够大的菱形,也不妨让学生进一步思考有没有面积最大的菱形,从而拓开学生的思维。) 利用白板的“直尺、圆规”、“线”工具进行作图,“笔”工具做标识和注释。
(二)应用练习--2 让学生能够综合运用平行四边形、矩形、菱形、正方形的判定解决问题,领悟到“三角形全等”是解决四边形问题常用而有效地方法,在综合解决问题时若给了结论而需补充条件应学会“逆向思维”。 2、已知△ABC,以三边为边分别作等边△ACD、△ABF、△BCE,判断四边形ADEF的形状。探究:①是否一定存在平行四边形ADEF,若存在写出△ABC应满足的条件;若不一定存在,请说明理由。②△ABC满足什么条件时,四边形ADEF是矩形?③△ABC满足什么条件时,四边形ADEF是菱形?④△ABC满足什么条件时,四边形ADEF是正方形? 课前:教师活动:设计学案,指导学生完成学案。学生活动:按照“学案”导学独立解决应用练习2所提出的问题。课中:教师活动1:针对学生回答的内容作斧正指导。学生活动1:小组代表讲解“判断四边形ADEF的形状”的方法和理由,其余学生认真聆听并作补充。教师活动2:动态演示满足矩形、菱形、正方形的条件,并适时提出新问题。学生活动2:小组代表讲解“△ABC满足什么条件时,四边形ADEF是矩形、菱形、正方形?”并阐述理由和思考的方法,其余学生认真聆听并作补充。 利用白板的“笔”工具边讲解边注释;利用链接功能链接到“.gsp”文件,丰富白板的内容,“.gsp”文件在白板环境下进行动态演示和书写更方便,效果更好。
(三)作业思考 以“特殊四边形为载体”进行全等探究是一类常见的问题,这里需要学生牢固掌握各特殊四边形的性质特征,另外以“改变问题条件继续对原问题结论进行探究”的探究问题也很常见,这里应让学生领悟到在解决探究问题时应使用类比思想,按照原问题的思路方法进行,找准原问题得以解决的关键和实质。 已知:如图①,正方形ABCD,点G、E分别是边AB、BC的中点,过E点作AE的垂线交正方形外角的平分线于点F.求证:AE=EF 探究:①若E是BC上任意一点(不与B、C重合),过E点作AE的垂线交正方形外角的平分线于点F,AE与EF相等吗?(在图②中完成)②若E是BC延长线上一点,过E点作AE的垂线交正方形外角的平分线于点F,AE与EF相等吗?(在图③中完成) 课前:教师活动:设计学案,指导学生完成学案。学生活动:按照“学案”导学独立解决作业思考所提出的问题。课中:教师活动:针对学生回答的内容作斧正指导,引导学生找出问题得以解决的关键实质所在。学生活动:1、分小组合作交流独立解决问题过程中的收获和思考问题的方法,学生彼此之间碰撞出思维的火花。2、小组代表讲解问题得以证明缘由和思考的方法,分析探究①和探究②与原始问题有何联系,又有何不同,从而师生共同寻找两个探究问题解决的思路方法(即两个三角形全等最主要的原因是AG=CE或BG=BE,进而确定出点G的位置)。 利用白板的“笔” “线”“圆规、直尺”工具画图,作注释。
(四)小结反思 养成课课总结与反思的好习惯,促进学生不断进步与提高。 谈谈本节课的收获 还存在的问题有哪些? 教师活动:认真倾听学生的发言,并进行答疑解惑。学生活动:以个体为单位自由发言,谈自己的收获与提高以及还存在的问题。
