华东师大版七年级数学下册9.1.3 三角形的三边关系 教案
文档属性
| 名称 | 华东师大版七年级数学下册9.1.3 三角形的三边关系 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 561.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 14:21:46 | ||
图片预览

文档简介
《9.1.3三角形的三边关系》教学设计与反思
教学目标
1.通过实践操作,进一步理解三角形的三边关系,并会利用三角形三边关系解决有关问题;了解三角形的稳定性,能举例说明三角形稳定性在生活中的应用.
2.经历观察、动手实验、尺规画图、推理交流等活动过程,发展归纳、合情推理的能力,能有条理地、清晰地阐述自己的观点.
3.学会从数学的角度提出问题、探究结论,并能用所学知识解决问题,发展应用意识;学会与他人合作交流思维的过程和结果.
4.能积极参与数学学习活动,对数学有好奇心和求知欲;培养学生在数学学习中获得成功的体验,建立自信心.
教学重点
探索并证明三角形的三边关系以及三角形三边关系的实际应用.
教学难点
理解、掌握“三角形的任何两边的和大于第三边”的性质.
学情分析
在小学阶段,学生已经了解到三角形的任何两边的和大于第三边这一事实,但对这一规律的认识只停留在生活经验的基础上,从实际抽象成图形,还是有一定的难度.
教学过程
一、创设情境 激发兴趣
1.展示上海东方绿舟社会实践活动中的图片.
设计意图:激发学生的学习兴趣,使学生感受到数学来源于生活.
2.用所给材料制作一个三角形.
设计意图:让学生体会圆规在作三角形中的作用,为已知三边画三角形作好铺垫.
二、动手操作,合作交流
1.已知三边画三角形
做一做:画一个三角形,使它的三边长分别为8cm、6cm、5 cm.
设计意图:通过让学生探索已知三边画三角形的方法,体会在作图中用圆规的必要性.学会画三角形,为探索三角形的三边关系作好画图的铺垫,也为以后学习全等三角形的内容积累了一定的数学活动经验.
2.探究三角形的三边关系
试一试:现有5条已知长度的线段(单位:cm):2,2,3,4,6.任意选择三条线段画三角形,使它的三条边长分别为你所选择的三条线段长.
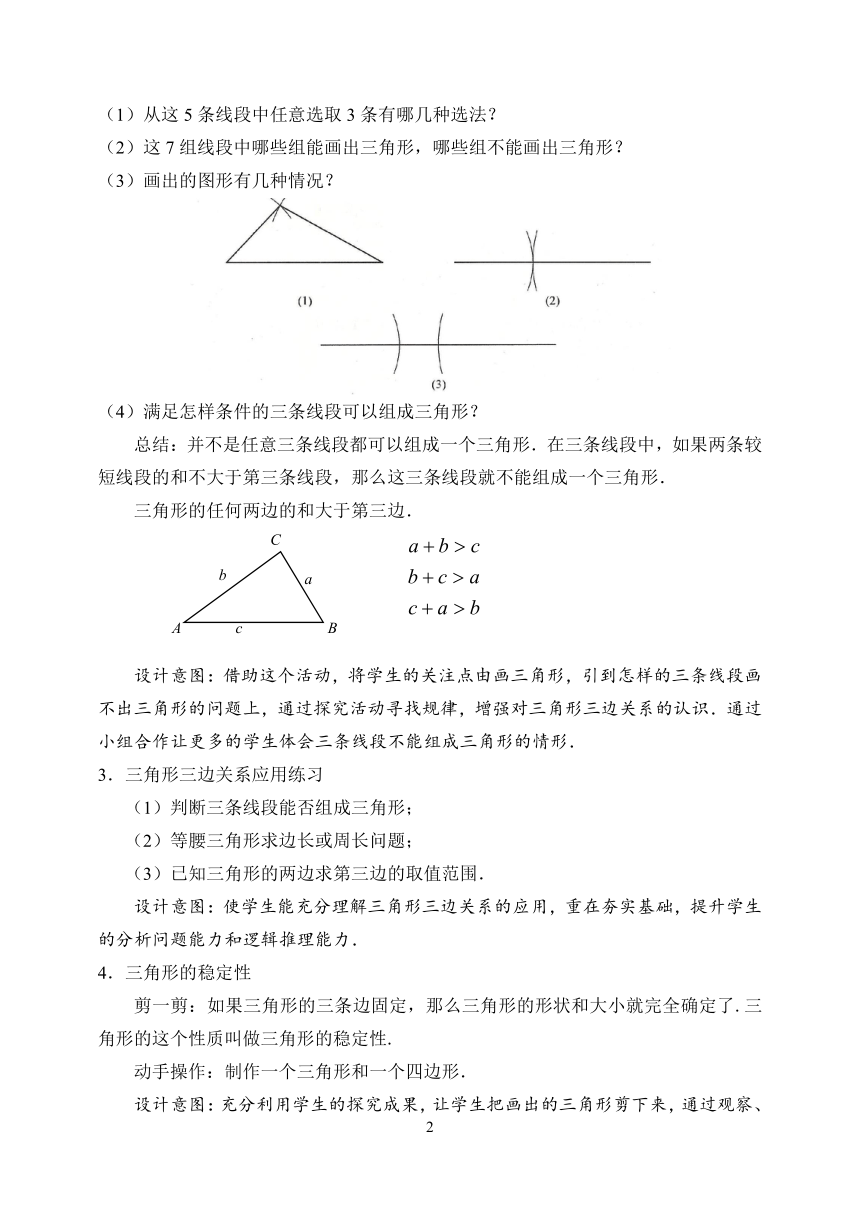
(1)从这5条线段中任意选取3条有哪几种选法?
(2)这7组线段中哪些组能画出三角形,哪些组不能画出三角形?
(3)画出的图形有几种情况?
(4)满足怎样条件的三条线段可以组成三角形?
总结:并不是任意三条线段都可以组成一个三角形.在三条线段中,如果两条较短线段的和不大于第三条线段,那么这三条线段就不能组成一个三角形.
三角形的任何两边的和大于第三边.
设计意图:借助这个活动,将学生的关注点由画三角形,引到怎样的三条线段画不出三角形的问题上,通过探究活动寻找规律,增强对三角形三边关系的认识.通过小组合作让更多的学生体会三条线段不能组成三角形的情形.
3.三角形三边关系应用练习
(1)判断三条线段能否组成三角形;
(2)等腰三角形求边长或周长问题;
(3)已知三角形的两边求第三边的取值范围.
设计意图:使学生能充分理解三角形三边关系的应用,重在夯实基础,提升学生的分析问题能力和逻辑推理能力.
4.三角形的稳定性
剪一剪:如果三角形的三条边固定,那么三角形的形状和大小就完全确定了.三角形的这个性质叫做三角形的稳定性.
动手操作:制作一个三角形和一个四边形.
设计意图:充分利用学生的探究成果,让学生把画出的三角形剪下来,通过观察、对比、分析,发现“如果三角形的三条边长确定,那么三角形的形状和大小就完全确定”这一事实,从而理解三角形的稳定性,也为学习三角形全等奠定基础.通过制作简单的小道具与四边形的不稳定性对比,让学生进一步体会三角形的稳定性.
教学设计说明
《数学课程标准》指出:“学生是数学学习的主人.”“数学学习内容应当是现实的、有意义的、富有挑战的,这些内容要有利于学生主动地进行观察、实验、猜测、验证、推理与交流等数学活动.” “动手实践、自主探索与合作交流是学生学习数学的重要方式.”
为体现新课标理念,本节课的教学采取了感知——探究——验证——应用的教学设计,充分发挥学生的主观能动性,创设优效课堂,体现我校数学学科“同修学习”的教学特色,大胆探索,寻求最优的教学方式.引导学生积极地参与到数学学习活动中,使学生真正成为学习的主人,充分体现了学生的主体地位.
教学反思
《三角形的三边关系》这节课是在小学学习的基础上通过画三角形的过程,验证三角形的三边关系,并体会三角形的三边关系的应用.
本节课的教学采取了感知——探究——验证——应用的教学设计,充分发挥学生的主观能动性,创设优效课堂,体现我校数学学科“同修学习”的教学特色,大胆探索,寻求最优的教学方式.
在引课部分利用我们刚刚结束的上海东方绿舟社会实践活动中的图片,引发学生的学习兴趣,使学生感受到数学来源于生活.通过动手制作三角形让学生体会圆规在作三角形中的作用,为已知三边画三角形作好铺垫.
通过让学生探索已知三边画三角形的方法,体会在作图中用圆规的必要性.学会画三角形,为探索三角形的三边关系作好画图的铺垫,也为以后学习全等三角形的内容积累了一定的数学活动经验.
在学生自主探索的活动中,设计从5条线段中任意选择三条线段画三角形,借助这个活动,将学生的关注点由画三角形,引到怎样的三条线段画不出三角形的问题上,通过探究活动寻找规律,增强对三角形三边关系的认识.通过小组合作让更多的学生体会三条线段不能组成三角形的情形.
在三角形三边关系的证明部分,采取画图和说理有机结合,引导学生用“两点之间,线段最短”来说明三角形三边关系,并用数学符号表示出来.
在学习稳定性时,充分利用学生的探究成果,让学生把画出的三角形剪下来,通过观察、对比、分析,发现“如果三角形的三条边长确定,那么三角形的形状和大小就完全确定”这一事实,从而理解三角形的稳定性,也为学习三角形全等奠定基础.通过制作简单的小道具与四边形的不稳定性对比,让学生进一步体会三角形的稳定性.
最后设计的练习环节,使学生能充分理解三角形三边关系的应用,重在夯实基础,提升学生的分析问题能力和逻辑推理能力.
成功之处:
1.通过制作三角形,使学生充分体会到画三角形中使用圆规的必要性.
在“画三条边长分别为8cm、6cm、5cm的三角形”中,许多同学先画出8cm和6cm的两条边,此时三角形已经确定,第三边不一定满足条件,通过演示制作的三角形,使学生明确:想要线段“动”起来,只有借助圆规,利用“圆上的任意一点与圆心的距离相等”来实现.
2.在探究“满足怎样条件的三条线段能组成三角形”中,设计从5条线段中任意选择三条线段画三角形,通过小组合作使更多的学生体会到三条线段不能组成三角形的情形.
3.三角形的三边关系应用的练习题中“等腰三角形求边长或周长问题”,渗透了数学中的分类思想.
4.在“已知三角形的两边求第三边的取值范围”问题中,采用了先“几何画板”演示,再利用三角形的三边关系与不等式的知识结合求解的方法,使学生由感性认识上升到理性认识.
5.同一系列的题型放在同一题组中,使学生可以在局部的训练中得到提高.
6.课堂气氛活跃,每一个学生都积极参与学习活动,达到了预期的教学目标.
不足之处:
1.在探索“满足怎样的三条线段能组成三角形”的过程中,虽然有小组合作,但没有充分发挥作用,如果能给小组内的同学充分沟通交流的机会,让学生自己探索出“在三条线段中,如果两条较短线段的和不大于第三条线段,那么这三条线段就不能组成一个三角形”就更好了.特别是对于“三角形的任何两边的和大于第三边”中的“任何”如何理解,如果能再给出一些实例,学生会理解的更好一些.
2.对于三角形稳定性认识还停留在感知的层面.
3.个别地方的处理效率不够高,在如何吸引学生的做法上还缺少有效的设计.
4.课堂讲解过多,没有把课堂真正还给学生,使学生成为学习的主人.
A c B
b
C
a
PAGE
1
教学目标
1.通过实践操作,进一步理解三角形的三边关系,并会利用三角形三边关系解决有关问题;了解三角形的稳定性,能举例说明三角形稳定性在生活中的应用.
2.经历观察、动手实验、尺规画图、推理交流等活动过程,发展归纳、合情推理的能力,能有条理地、清晰地阐述自己的观点.
3.学会从数学的角度提出问题、探究结论,并能用所学知识解决问题,发展应用意识;学会与他人合作交流思维的过程和结果.
4.能积极参与数学学习活动,对数学有好奇心和求知欲;培养学生在数学学习中获得成功的体验,建立自信心.
教学重点
探索并证明三角形的三边关系以及三角形三边关系的实际应用.
教学难点
理解、掌握“三角形的任何两边的和大于第三边”的性质.
学情分析
在小学阶段,学生已经了解到三角形的任何两边的和大于第三边这一事实,但对这一规律的认识只停留在生活经验的基础上,从实际抽象成图形,还是有一定的难度.
教学过程
一、创设情境 激发兴趣
1.展示上海东方绿舟社会实践活动中的图片.
设计意图:激发学生的学习兴趣,使学生感受到数学来源于生活.
2.用所给材料制作一个三角形.
设计意图:让学生体会圆规在作三角形中的作用,为已知三边画三角形作好铺垫.
二、动手操作,合作交流
1.已知三边画三角形
做一做:画一个三角形,使它的三边长分别为8cm、6cm、5 cm.
设计意图:通过让学生探索已知三边画三角形的方法,体会在作图中用圆规的必要性.学会画三角形,为探索三角形的三边关系作好画图的铺垫,也为以后学习全等三角形的内容积累了一定的数学活动经验.
2.探究三角形的三边关系
试一试:现有5条已知长度的线段(单位:cm):2,2,3,4,6.任意选择三条线段画三角形,使它的三条边长分别为你所选择的三条线段长.
(1)从这5条线段中任意选取3条有哪几种选法?
(2)这7组线段中哪些组能画出三角形,哪些组不能画出三角形?
(3)画出的图形有几种情况?
(4)满足怎样条件的三条线段可以组成三角形?
总结:并不是任意三条线段都可以组成一个三角形.在三条线段中,如果两条较短线段的和不大于第三条线段,那么这三条线段就不能组成一个三角形.
三角形的任何两边的和大于第三边.
设计意图:借助这个活动,将学生的关注点由画三角形,引到怎样的三条线段画不出三角形的问题上,通过探究活动寻找规律,增强对三角形三边关系的认识.通过小组合作让更多的学生体会三条线段不能组成三角形的情形.
3.三角形三边关系应用练习
(1)判断三条线段能否组成三角形;
(2)等腰三角形求边长或周长问题;
(3)已知三角形的两边求第三边的取值范围.
设计意图:使学生能充分理解三角形三边关系的应用,重在夯实基础,提升学生的分析问题能力和逻辑推理能力.
4.三角形的稳定性
剪一剪:如果三角形的三条边固定,那么三角形的形状和大小就完全确定了.三角形的这个性质叫做三角形的稳定性.
动手操作:制作一个三角形和一个四边形.
设计意图:充分利用学生的探究成果,让学生把画出的三角形剪下来,通过观察、对比、分析,发现“如果三角形的三条边长确定,那么三角形的形状和大小就完全确定”这一事实,从而理解三角形的稳定性,也为学习三角形全等奠定基础.通过制作简单的小道具与四边形的不稳定性对比,让学生进一步体会三角形的稳定性.
教学设计说明
《数学课程标准》指出:“学生是数学学习的主人.”“数学学习内容应当是现实的、有意义的、富有挑战的,这些内容要有利于学生主动地进行观察、实验、猜测、验证、推理与交流等数学活动.” “动手实践、自主探索与合作交流是学生学习数学的重要方式.”
为体现新课标理念,本节课的教学采取了感知——探究——验证——应用的教学设计,充分发挥学生的主观能动性,创设优效课堂,体现我校数学学科“同修学习”的教学特色,大胆探索,寻求最优的教学方式.引导学生积极地参与到数学学习活动中,使学生真正成为学习的主人,充分体现了学生的主体地位.
教学反思
《三角形的三边关系》这节课是在小学学习的基础上通过画三角形的过程,验证三角形的三边关系,并体会三角形的三边关系的应用.
本节课的教学采取了感知——探究——验证——应用的教学设计,充分发挥学生的主观能动性,创设优效课堂,体现我校数学学科“同修学习”的教学特色,大胆探索,寻求最优的教学方式.
在引课部分利用我们刚刚结束的上海东方绿舟社会实践活动中的图片,引发学生的学习兴趣,使学生感受到数学来源于生活.通过动手制作三角形让学生体会圆规在作三角形中的作用,为已知三边画三角形作好铺垫.
通过让学生探索已知三边画三角形的方法,体会在作图中用圆规的必要性.学会画三角形,为探索三角形的三边关系作好画图的铺垫,也为以后学习全等三角形的内容积累了一定的数学活动经验.
在学生自主探索的活动中,设计从5条线段中任意选择三条线段画三角形,借助这个活动,将学生的关注点由画三角形,引到怎样的三条线段画不出三角形的问题上,通过探究活动寻找规律,增强对三角形三边关系的认识.通过小组合作让更多的学生体会三条线段不能组成三角形的情形.
在三角形三边关系的证明部分,采取画图和说理有机结合,引导学生用“两点之间,线段最短”来说明三角形三边关系,并用数学符号表示出来.
在学习稳定性时,充分利用学生的探究成果,让学生把画出的三角形剪下来,通过观察、对比、分析,发现“如果三角形的三条边长确定,那么三角形的形状和大小就完全确定”这一事实,从而理解三角形的稳定性,也为学习三角形全等奠定基础.通过制作简单的小道具与四边形的不稳定性对比,让学生进一步体会三角形的稳定性.
最后设计的练习环节,使学生能充分理解三角形三边关系的应用,重在夯实基础,提升学生的分析问题能力和逻辑推理能力.
成功之处:
1.通过制作三角形,使学生充分体会到画三角形中使用圆规的必要性.
在“画三条边长分别为8cm、6cm、5cm的三角形”中,许多同学先画出8cm和6cm的两条边,此时三角形已经确定,第三边不一定满足条件,通过演示制作的三角形,使学生明确:想要线段“动”起来,只有借助圆规,利用“圆上的任意一点与圆心的距离相等”来实现.
2.在探究“满足怎样条件的三条线段能组成三角形”中,设计从5条线段中任意选择三条线段画三角形,通过小组合作使更多的学生体会到三条线段不能组成三角形的情形.
3.三角形的三边关系应用的练习题中“等腰三角形求边长或周长问题”,渗透了数学中的分类思想.
4.在“已知三角形的两边求第三边的取值范围”问题中,采用了先“几何画板”演示,再利用三角形的三边关系与不等式的知识结合求解的方法,使学生由感性认识上升到理性认识.
5.同一系列的题型放在同一题组中,使学生可以在局部的训练中得到提高.
6.课堂气氛活跃,每一个学生都积极参与学习活动,达到了预期的教学目标.
不足之处:
1.在探索“满足怎样的三条线段能组成三角形”的过程中,虽然有小组合作,但没有充分发挥作用,如果能给小组内的同学充分沟通交流的机会,让学生自己探索出“在三条线段中,如果两条较短线段的和不大于第三条线段,那么这三条线段就不能组成一个三角形”就更好了.特别是对于“三角形的任何两边的和大于第三边”中的“任何”如何理解,如果能再给出一些实例,学生会理解的更好一些.
2.对于三角形稳定性认识还停留在感知的层面.
3.个别地方的处理效率不够高,在如何吸引学生的做法上还缺少有效的设计.
4.课堂讲解过多,没有把课堂真正还给学生,使学生成为学习的主人.
A c B
b
C
a
PAGE
1
